\(x^2(x-1)(x-4)-2x^3=-6x^2\)
If x > 0, what is one possible solution to the equation above? (Hint: there are two real solutions)
Answers
Answer:
2 and 5Step-by-step explanation:
Solving in steps
x^2(x - 1)(x - 4) - 2x^3 = -6x^2, x > 0x^2(x^2 - 5x + 4) -2x^3 + 6x^2 = 0x^4 - 5x^3 + 4x^2 - 2x^3 + 6x^2 = 0x^4 - 7 x^3 + 10x^2 = 0x^2 - 7x + 10 = 0x^2 - 2x - 5x + 10 = 0x(x - 2) - 5(x - 2) = 0(x - 2)( x - 5) = 0x - 2 = 0 ⇒ x = 2x - 5 = 0 ⇒ x = 5Answer:
x = 2 and 5
Step-by-step explanation:
x²(x - 1)(x - 4) - 2x³ = -6x² when x > 0
x²(x - 1)(x - 4) - 2x³ + 6x² = 0
~Use foil to simplify the stuff in parenthesis
x⁴ - 5x³ + 4x² - 2x³ + 6x² = 0
~Combine like terms
x⁴ - 7x³ + 10x² = 0
~Factor
x(x - 2) - 5(x - 2)
~Simplify
(x - 2)(x - 5) = 0
~Solve both factors
x - 2 = 0
x = 2
x - 5 = 0
x = 5
Best of Luck!
Related Questions
One employee of a computer store is paid a base salary of MK21,500 a month plus an 8% commission on all sales over MK70,000 during the month. How much must the employee sell in 1 month to earn a total of MK31,700 for the month?
Answers
Answer:
I think the total sales must equal $32000
Step-by-step explanation:
Given,
Base Salery = $2000
Commission = 8% in sales above 7000
To find out how much sales should be made so that the total earnings are $4000. Let the sales be x. Then the required linear equation is
2000 + 0.08 ( x - 7000) = 4000
2000 + 0.08x - 560 = 4000 (Using distributive property)
1440 + 0.08x = 4000 (Simplifying)
0.08x = 2560 (Subtacting 1440 from both sides)
x = 2560/0.08 (Dividing both sides by 0.08)
x = 32000
Thus, total sales must equal $32000
I hope this help you!
consider carrying out m tests of hypotheses based on independent samples, each at significance level (exactly) 0.01. (a) what is the probability of committing at least one type i error when m
Answers
The probability of committing when at least one type I error at a significance level (exactly) 0.01 at m = 11 is equivalent to 0.1047.
Given that:
The hypotheses are based on independent samples with each at a 0.01 level of significance.
We know that:
P (at least one type I error is committed) = 1 - [P (No error - type I error is committed)]^m
P (at least one type I error is committed) = 1 - [(1 - 0.01)]^11
P (at least one type I error is committed) = 1 - [0.99]^11
P (at least one type I error is committed) = 1 - 0.8953
P (at least one type I error is committed) = 0.1047
So, the probability of committing when at least one type I error is equivalent to 0.1047.
To learn more about the probability visit: https://brainly.com/question/11234923
#SPJ4
help me please. my mom will take away my kitten

Answers
Answer:
-4x + 6
Step-by-step explanation:
5x - 9x + 8 - 2
(5x - 9x) + (8 - 2)
-4x + 6
Answer:
The x terms are -4x
Step-by-step explanation:
The constanets=6
So the equation would be -4x+6
Hope this helps!
find the two rational number between -2 and-1
Answers
Answer:
-3/2, -7/4
Step-by-step explanation:
The numbers have to be negative, and two rational numbers between -1 and -2 are -1.5 and -1.75 and fortunately for us, both are rational (can be expressed as fractions), -1.5 = -3/2 and -1.75 = -7/4
HPH (Happy to help)
for the function g on [0, /2], find the average value gave. g(x) = e^sin(x) cos(x),
Answers
To find the average value of the function g(x) = e^sin(x) cos(x) on the interval [0, π/2], we need to compute the definite integral of g(x) over the interval and divide by the length of the interval.
The average value of a continuous function f(x) over an interval [a, b] is defined as:
Avg. value = (1 / (b - a)) * ∫[a, b] f(x) dx
In this case, the function g(x) is continuous on the interval [0, π/2], so we can use the above formula to find its average value over the interval. The definite integral of g(x) on the interval [0, π/2] is:
∫[0, π/2] e^sin(x) cos(x) dx
This integral can be evaluated using integration by substitution, with u = sin(x) and du = cos(x) dx. Thus:
∫[0, π/2] e^sin(x) cos(x) dx = ∫[0, 1] e^u du
= e^u ∣[0, 1] = e^1 - e^0 = e - 1
Therefore, the average value of g(x) on the interval [0, π/2] is:
Avg. value = (1 / (π/2 - 0)) * ∫[0, π/2] e^sin(x) cos(x) dx
= (2 / π) * (e - 1)
So the average value of g(x) on the interval [0, π/2] is (2 / π) * (e - 1).
Learn more about functions here:
https://brainly.com/question/31062578
#SPJ11
Determine whether the given set S is a subspace of the vector space V.
A. V=P5, and S is the subset of P5 consisting of those polynomials satisfying p(1)>p(0).
B. V=ℝ3, and S is the set of vectors (x1,x2,x3) in V satisfying x1−6x2+x3=5.
C. V=ℝn, and S is the set of solutions to the homogeneous linear system Ax=0 where A is a fixed m×n matrix.
D. V=C2(I), and S is the subset of V consisting of those functions satisfying the differential equation y″−4y′+3y=0.
E. V is the vector space of all real-valued functions defined on the interval [a,b], and S is the subset of V consisting of those functions satisfying f(a)=5.
F. V=Pn, and S is the subset of Pn consisting of those polynomials satisfying p(0)=0.
G. V=Mn(ℝ), and S is the subset of all symmetric matrices
Answers
(a) Given that V=P5, and S is the subset of P5 consisting of those polynomials satisfying p(1)>p(0).We know that p(1) > p(0) is a linear function as it satisfies the following criteria:If p and q are two polynomials satisfying p(1) > p(0) and q(1) > q(0), then for any real number c, cp+q(1) > cp+q(0).
Therefore, S is a subspace of P5.(b) Let V=ℝ3, and S is the set of vectors (x1,x2,x3) in V satisfying x1−6x2+x3=5.The zero vector, (0,0,0), is not in S since 0−6(0)+0=0 ≠ 5. Therefore, S is not a subspace of V.(c) Let V=ℝn, and S is the set of solutions to the homogeneous linear system Ax=0 where A is a fixed m×n matrix.Ax=0 is a homogeneous linear system. Therefore, the trivial solution x=0 is in S. Therefore, S is a subspace of V.(d) Let V=C2(I), and S is the subset of V consisting of those functions satisfying the differential equation y″−4y′+3y=0.The zero function, y=0, is in S. If f and g are in S, then f+g and cf are also in S for any scalar c. Therefore, S is a subspace of V.(e) Let V be the vector space of all real-valued functions defined on the interval [a,b], and S is the subset of V consisting of those functions satisfying f(a)=5.The zero function, f(x)=0, is in S. If f and g are in S, then f+g and cf are also in S for any scalar c. Therefore, S is a subspace of V.(f) Given that V=Pn, and S is the subset of Pn consisting of those polynomials satisfying p(0)=0.The zero polynomial, p(x)=0, is in S. If p and q are in S, then p+q and cp are also in S for any scalar c. Therefore, S is a subspace of V.(g) Let V=Mn(ℝ), and S is the subset of all symmetric matricesThe zero matrix, 0, is in S. If A and B are symmetric, then A+B and cA are also symmetric. Therefore, S is a subspace of V.
To know more about subspace visit:
https://brainly.com/question/15580495
#SPJ11
Helppppppppppppppppppppp I need this ASAP

Answers
ASAP
- WILL MARK BRIANIST

Answers
Now Mark me Brainiest
PLEASE WILL MARK BRAINLIST
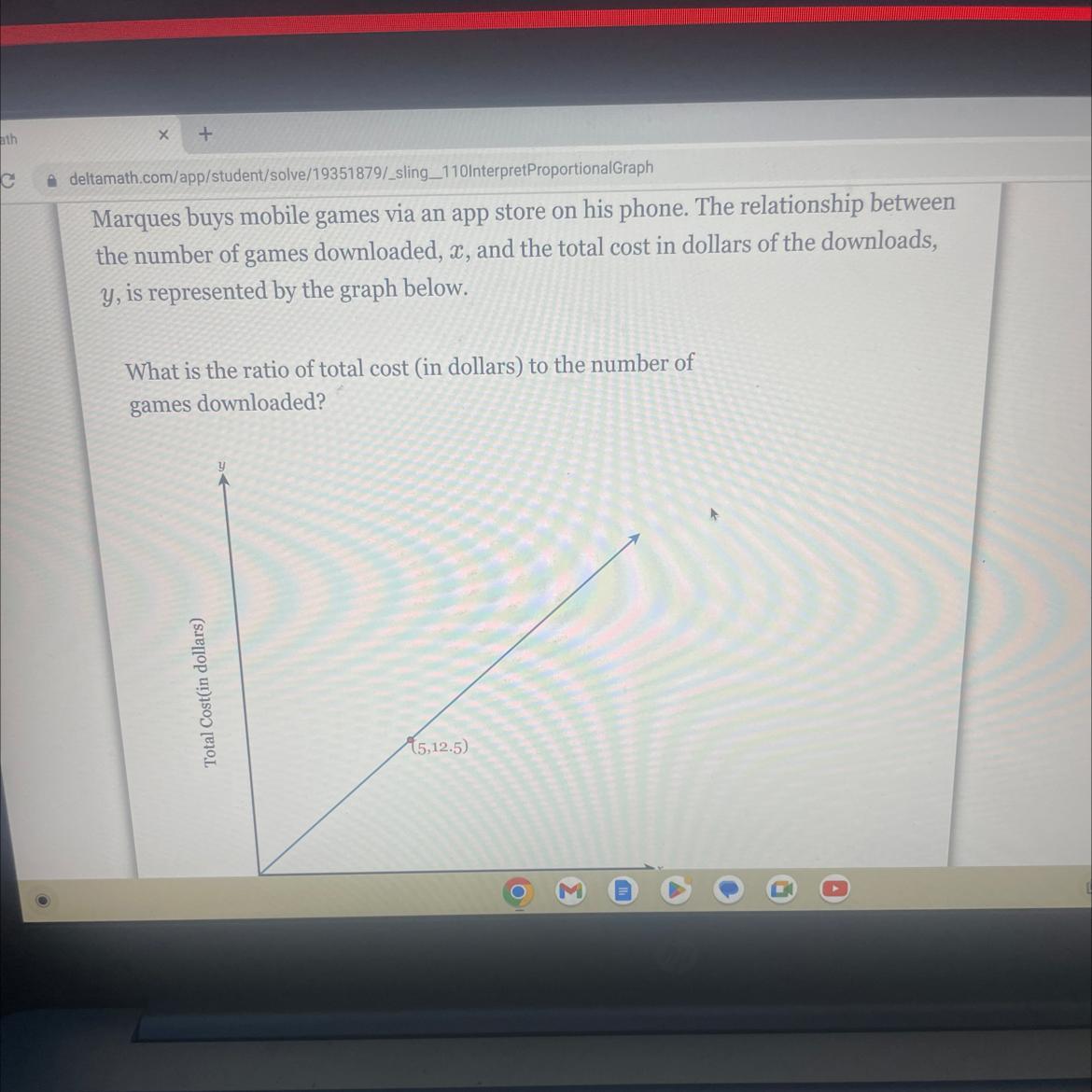
Answers
The graph represents the relationship between the number of games downloaded and the total cost in dollars. The ratio of total cost to the number of games downloaded is $2.50 per game.
The given graph shows the relationship between the number of games downloaded and the total cost in dollars of the downloads. It can be observed that when 2 games are downloaded, the total cost is $5.
To determine the ratio of total cost to the number of games downloaded, we divide the total cost by the number of games.
This results in a ratio of $2.50 per game downloaded. Thus, the ratio of total cost (in dollars) to the number of games downloaded is $2.50 per game.
This means that on average, each game downloaded costs $2.50.
For more questions like Costs click the link below:
brainly.com/question/31041508
#SPJ1
determine the radius and center of the circle with the following equation
x^2+y^2-12x+24y-10=6
Answers
Answer:
Center: (6, -12)
Radius: 4
Step-by-step explanation:
Complete the squares
\(x^2+y^2-12x+24y-10=6\\\\x^2-12x-10+y^2+24y=6\\\\x^2-12x-10+46+y^2+24y+144=6+46+144\\\\(x^2-12x+36)+(y^2+24y+144)=196\\\\(x-6)^2+(y+12)^2=196\)
Comparing with the standard form equation \((x-h)^2+(y-k)^2=r^2\), since \(r^2=196\), then the radius of the circle is \(r=14\). Also, the center of the circle would be \((h,k)\rightarrow(6,-12)\).
A block measure 22cm by 11cm by 7cm. How many of these blocks will be needed to build a wall 5 1/2m long, 22cm thick and 3 1/2m high.
Answers
Answer:
The number of blocks that will be needed to build the wall is 2500
Step-by-step explanation:
The number of blocks that will be needed to build the wall is;
\(n = \frac{volume of wall}{volume of block} \\volume = l *b*h\\\)
given the dimensions of the block and wall as;
block = 22cm by 11cm by 7cm
wall = 5 1/2m long, 22cm thick and 3 1/2m high. = 550cm by 22cm by 350cm
substituting into the equation, we have;
\(n = \frac{volume of wall}{volume of block} \\volume = l *b*h\\\\n = \frac{550*22*350}{22*11*7} \\n = 2500\)
The number of blocks that will be needed to build the wall is 2500
There are 240 students going on a field trip. Each school bus can hold 48 students. Complete the equation to show which operation to use and how many school buses are needed.
Answers
Answer:
240÷48=5 no of buses needed, use division
What is the GCE of 95 and 120 :
Answers
Answer:
the answer to the question is 5
Answer:
did you mean GCF if so its 30
2 word problems using quadratic formula. Triple points!!

Answers
According to quadratic equations, the travelling time of each ball is, respectively:
Case 7: t = 3.203 s.
Case 8: t = 4.763 s.
How to determine the travelling time of a ball in the air
In this problem we find two word problems involving a ball travelling in the air, whose motion equation is described by a quadratic equation:
h = - 16 · t² + v · t + c
Where:
v - Initial speed, in feet per second.c - Initial height, in feet.t - Time, in seconds.Travelling time can be found by following conditions: (h = 0)
- 16 · t² + v · t + c = 0
t = v / 32 ± (1 / 32) · √(v² + 64 · c), where t > 0.
Now we proceed to determine the resulting time:
Case 7: (v = 50 ft / s, c = 4 ft)
t = 50 / 32 ± (1 / 32) · √(50² + 64 · 4)
t = 3.203 s.
Case 8: (v = 76 ft / s, c = 1 ft)
t = 76 / 32 ± (1 / 32) · √(76² + 64 · 1)
t = 4.763 s.
To learn more on quadratic equation: https://brainly.com/question/1863222
#SPJ1
45.1 devided by 1,000
Answers
1,305 divided by 31,828 x100
Answers
Answer:
\(4 \frac{1}{10}\)
Step-by-step explanation:
=> \(\frac{1305}{31828} * 100\)
=> 0.041 * 100
=> 4.1
=> \(4 \frac{1}{10}\)
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
Use the divergence theorem to compute the net outward flux of the vector field f across the boundary of the region d. F= 32-x,x - 5y,7y +9z
Answers
Using the divergence theorem we can compute that the outward flux of the vector field is 16π .
The outward flux of F over the solid cylinder and z = 0 is
∫∫F·ds = ∫∫∫ DivF dv
F = 2xy² i + 2x²y j + 2xy k
Div F = D/dx (2xy²) + D/dy (2x²y )
Div F = 2y² + 2x²
In cylindrical coordinates dV = rdrdθdz and as z = 0 the region is a surface ds = r·dr·dθ
Using the parametric form of the surface equation
x = rcosθ y = r sinθ and z = z
Div F = 2r² sin²θ + 2r²cos²θ
∫∫∫ DivF dv = ∫∫ [2r²sin²θ + 2r²cos²θ] × rdrdθ
∫∫ 2r² [sin²θ + cos²θ] × rdrdθdz ⇒ ∫∫ 2r³ drdθ
Integration limits
0 < r < 2 0 < θ < 2π
2∫₀² r³ ∫dθ
(2/4) × (2)⁴ × 2π
The divergence theorem, commonly known as Gauss' theorem or Ostrogradsky's theorem, is a theorem that connects the flow of a vector field across a closed surface to the field's divergence in the volume enclosed.
In more detail, the divergence theorem states that the surface integral of a vector field across a closed surface, sometimes referred to as the "flux" through the surface, is equal to the volume integral of the divergence over the region inside the surface.
Therefore the flux is 16π .
To know more details about flux visit:
brainly.com/question/16840837
#SPJ4
A spinner is spun twice with 4 equal sections colored purple, red, green, and blue. What is the P(spinning one Red and one Green)? 1 over 4 1 over 6 1 over 8 1 over 16
Answers
The probability of spinning two greens on the spinner is equal to 1/16.
We need to find the probability of spinning a green on the first spin and then the probability of spinning another green on the second spin.
Since 4 equal sections on the spinner and one of them is green, the probability of spinning a green on the first spin is 1/4.
Therefore, the probability of spinning a green on the second spin is; 1/4.
P(spinning two greens) = P(green on first spin) x P(green on second spin)
= (1/4) * (1/4)
= 1/16
Therefore, the probability of spinning two greens on the spinner = 1/16.
learn more about "probability":-
brainly.com/question/25839839
#SPJ1
Find the inverse function.
f(x) =
f-¹(x) =
=
=
2x+5
4
4x + [?]
[
![Find the inverse function.f(x) =f-(x) ===2x+544x + [?][](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/hhvAQEzFwZkDVi2flrjvk7PArSGoTBQD.png)
Answers
Answer: \(f^{-1} (x)=\frac{4x-5}{2}\)
Step-by-step explanation:
Let \(f(y)=x\\\).
\(\implies x=\frac{2y+5}{4}\\\\4x=2y+5\\\\4x-5=2y\\\\y=\frac{4x-5}{2}\\\\\therefore f^{-1} (x)=\frac{4x-5}{2}\)
Which expression can be written as 7(c + d)
→ 7c x 7d
→ 7c + d
→ c + 7d
→ 7c + 7d
Answers
Answer:
→ 7c + 7d
Step-by-step explanation:
7(c+d)7×c + 7×d7c + 7dThus, 7c + 7d can be written as 7(c + d)
Chelsea went ice-skating. The ice, her skates, the Zamboni, and the rink building itself were all examples of solids she encountered. She developed a model of the particles in the ice. Which of these statements about the particles present in her model of a solid are true? Choose the three statements that apply.
A.They vibrate in place
B.They slide past each other.
C.They are packed very closely together.
D.They cause the solid to have definite volume and shape.
Answers
Which choice is equivalent to the expression below?
-25

Answers
Answer:
5i
Step-by-step explanation:
Answer:
5i
Step-by-step explanation:
sqrt( -25)
Rewriting
sqrt( 25 * -1)
We know that sqrt(ab) = sqrt(a) sqrt(b)
sqrt(25) sqrt(-1)
We know that sqrt(-1) = i
±5 i
Distance between (7,-2) and (-1,-1)
Answers
Answer: The distance formula between two points (x1, y1) and (x2, y2) is:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Using this formula, we can find the distance between (7, -2) and (-1, -1):
d = sqrt((-1 - 7)^2 + (-1 - (-2))^2)
= sqrt((-8)^2 + (1)^2)
= sqrt(64 + 1)
= sqrt(65)
Therefore, the distance between (7, -2) and (-1, -1) is sqrt(65), or approximately 8.06 units.
Step-by-step explanation:
Instructions: Based on the scale of measurement for the data, identify if a test is parametric or nonparametric.
A researcher measures the proportion of schizophrenic patients born in each season.
A researcher measures the average age that schizophrenia is diagnosed among male and female patients.
A researcher tests whether frequency of Internet use and social interaction are independent.
A researcher measures the amount of time (in seconds) that a group of teenagers uses the Internet for school-related and non-school-related purposes.
Please provide reasoning for your answer.
Answers
It is important to consider the scale of measurement and the specific characteristics of the variables when selecting an appropriate statistical test.The tests can be classified as follows:
1. A researcher measures the proportion of schizophrenic patients born in each season.
This test is nonparametric. The scale of measurement is categorical, as the seasons (spring, summer, fall, winter) represent distinct categories rather than continuous numerical values. Therefore, parametric assumptions, such as normality and equal variances, do not apply to this measurement.
2. A researcher measures the average age that schizophrenia is diagnosed among male and female patients.
This test is parametric. The scale of measurement is continuous and numerical (age in years). Parametric tests, such as t-tests or ANOVA, can be applied when working with continuous data, assuming the data meet the required assumptions (e.g., normality, independence, and equal variances).
3. A researcher tests whether frequency of Internet use and social interaction are independent.
This test can be both parametric or nonparametric, depending on the measurement scale and the specific statistical test used. If the variables are measured on a nominal or ordinal scale, nonparametric tests, such as the chi-square test, would be appropriate. If the variables are measured on a continuous scale, parametric tests, such as logistic regression, could be employed.
4. A researcher measures the amount of time (in seconds) that a group of teenagers uses the Internet for school-related and non-school-related purposes.
This test is parametric. The scale of measurement is continuous (time in seconds), and parametric tests, such as t-tests or ANOVA, can be utilized to compare means or variances, assuming the required assumptions are met.
know more about researcher :brainly.com/question/24174276
#SPJ11
A confectionery company mixes three types of toffees to form one kilogram " toffee packs. the pack is sold at rs. 17. the three types of toffees cost rs.20, rs. 10, rs. 5 per kg. resp. the mixture must contain atleast 300 gms of first type. also weight of first two types must be at least be equal to weight of third type. find the optimal mix for maximum profit.answer
Answers
The maximum profit is 6 and it is obtained when we mix 0.6 kg of type A, 0 kg of type B, and 0.4 kg of type C.
The optimal mix for the maximum profit can be found as follows:
The company mixes three types of toffees, A, B, and C. Let the weights of type A, B, and C be a, b, and c kg, respectively. Let us assume that we are making 1kg of toffee pack. Therefore, the weight of type C should be 1 - (a + b) kg. Also, the mixture must contain at least 300 gms of type A i.e a >= 0.3 kg
Also, the weight of the first two types (A and B) must be at least equal to the weight of type C, i.e a + b >= c. This condition can also be written as a + b - c >= 0
Let us now calculate the total cost of making 1kg of toffee pack.
Cost = 20a + 10b + 5c
If the pack is sold at Rs. 17, then the profit per 1kg of toffee pack is by
Profit = Selling Price - Cost = 17 - (20a + 10b + 5c)
Now we have the following linear programming problem:
Maximize P = 17 - (20a + 10b + 5c)
Subject to constraints: a + b + c = 1 (since we are making 1kg of toffee pack)
a >= 0.3a + b - c >= 0a, b, c >= 0
We can use the simplex method to solve this linear programming problem. However, to save time, we can solve it graphically. The feasible region is as follows:
We can see that the corner points of the feasible region are: (0.3, 0, 0.7), (0.6, 0, 0.4), (0, 0.5, 0.5), and (0, 1, 0).
Let us calculate the profit at each of these corner points. For example, at the point (0.3, 0, 0.7), we have a = 0.3, b = 0, and c = 0.7. Therefore, the profit is
P = 17 - (20(0.3) + 10(0) + 5(0.7)) = 3.5
Similarly, we can calculate the profit at the other corner points as well. The corner point (0.3, 0, 0.7) gives a profit of 3.5
Corner point (0.6, 0, 0.4) result in a profit of 6
Corner point (0, 0.5, 0.5) results in a profit of 5
Corner point (0, 1, 0) gives a profit of 3
You can learn more about optimal mix at: brainly.com/question/30629565
#SPJ11
sqrt2+sqrt2/sqrt2-sqrt5 what is the simplest form of the radical expression
Answers
Answer:
- (4+2sqrt10)/3
Step-by-step explanation:
The only reason this problem needs to be worked on is that you can't have a radical on the bottom of a fraction(rational expression) . We'll use the CONJUGATE of the denominator(expression on the bottom) to get rid of the radicals.
The conjugate has the same terms as the bottom expression, but it has the OPPOSITE sign in between. Your question has
(root2 - root5). Then the CONJUGATE is
(root2 + root5).
We can't just randomly change the denominator of a number, so we will have to multiply the top by
(root2 + root5) also.
see image.
Multiplying these terms is very similar to multiplying binomials. Use distributive property or, if you know the method, FOIL. You may have learned a box method. This multplication is shown with the arrows in the attached image.
see image.

20 POINTS PLS HELP ME Find the surface area of each pyramid. Round to the nearest tenth if necessary.

Answers
Answer:
633.94 squared inches
Step-by-step explanation:
15.75 x 15.75 = 248.0625
12.25 x 15.75 x 1/2 = 96.46875
since there are 4 triangles and they are equivalent...
96.46875 x 4 = 385.875
Surface area is...
385.875 + 248.0625 = 633.9375
changing my answer hh
Evaluate:
will give brainliest

Answers
Answer:
80
Step-by-step explanation:
S4 = 2(3°+3¹+3²+3³)
= 2(1+3+9+27)
= 2(40)
= 80
oliver has 5 pieces of string that are each 4 2 12 feet long. destiny has 4 pieces of string that are each 5 14 16 feet long. use an estimation strategy to determine who has the most string. choose the name and number to complete the statement. choose... is estimated to have choose... more feet of string.
Answers
Oliver has 5 pieces of string each of length 4 2 12 feet and Destiny has 4 pieces of string each of length 5 14 16 feet.
Now, let's use an estimation strategy to determine who has the most string by rounding the length of each string to the nearest whole number.The nearest whole number to 4 2 12 is 4The nearest whole number to 5 14 16 is 6Now, we can determine who has the most string by multiplying the rounded lengths of each string by the number of strings they have:Oliver has 5 strings, so he has about 5 × 4 = 20 feet of stringDestiny has 4 strings, so she has about 4 × 6 = 24 feet of string
Therefore, Destiny is estimated to have about 24 − 20 = 4 more feet of string than Oliver. Thus, Destiny is estimated to have 4 more feet of string than Oliver.
To know more about estimation visit:
https://brainly.com/question/30876115
#SPJ11