In a math class with 28 students, a test was given the same day that an assignment
was due. There were 18 students who passed the test and 23 students who completed
the assignment. There were 16 students who passed the test and also completed the
assignment. What is the probability that a student who passed the test did not
complete the homework?
Answers
Answer:
Probability that a student who passed the test did not complete the homework = 0.07
Step-by-step explanation:
Given:
Total number of students = 28
Number of students who passed the test = 18
Number of students who completed the assignment = 23
Number of students who passed the test and also completed the assignment = 16
To find: probability that a student who passed the test did not complete the homework
Solution:
Probability refers to chances of occurrence of some event.
Probability = number of favorable outcomes/total number of outcomes
Let A denotes the event that students passed the test and B denotes the event that students completed the assignment
P(A only) = \(P(A)-P(A\cap B)\)
Here,
\(P(A)=\frac{18}{28}\,,\,P(A\cap B)=\frac{16}{28}\)
So,
\(P(A\,\,only)=\frac{18}{28}-\frac{16}{28}=\frac{2}{28}=\frac{1}{14}=0.07\)
Therefore,
probability that a student who passed the test did not complete the homework = 0.07
Answer:
2/9
Step-by-step explanation:
Related Questions
a penny is dropped into a well. it takes 5 seconds to fall. calculate the depth of the well in feet. choose... ft
Answers
The calculated depth of the well in feet is 402.5 feet
How to calculate the depth of the well in feetFrom the question, we have the following parameters that can be used in our computation:
Time, t = 5 seconds
The depth of the well in feet is calculated as
d = 1/2gt²
substitute the known values in the above equation, so, we have the following representation
d = 1/2 * 32.2 * 5²
Evaluate
d = 402.5
Hence, the depth is 402.5 feet
Read more about height functions at
https://brainly.com/question/10837575
#SPJ4
Which of the following is the solution to the differential equation yệt) 1 t 17 with initial condition y(1) ? 12 5 t6 a) 17 85 66t2 132t4 b) 17 85 6916 92t8 c) t6 5t4 6 4 d) 851 1714 52 78
Answers
The solution to the differential equation y''(t) = 1 - t^17 with initial condition y(1) = 12 is:
y(t) = (1/2)t^2 - (1/342)t^19 + (217/18)t + (19805/342)
None of the provided options (a, b, c, d) match the correct solution.
To solve the given differential equation y''(t) = 1 - t^17 with the initial condition y(1) = 12, we can integrate the equation twice.
Integrating the equation once will give us y'(t):
y'(t) = ∫(1 - t^17) dt
y'(t) = t - (1/18)t^18 + C₁
Now, we need to apply the initial condition y(1) = 12 to determine the value of the constant C₁:
12 = 1 - (1/18) + C₁
C₁ = 12 + (1/18) - 1
C₁ = 217/18
Next, we integrate y'(t) to find y(t):
y(t) = ∫(t - (1/18)t^18 + 217/18) dt
y(t) = (1/2)t^2 - (1/342)t^19 + (217/18)t + C₂
Finally, we apply the initial condition y(1) = 12 to determine the value of the constant C₂:
12 = (1/2) - (1/342) + (217/18) + C₂
C₂ = 12 - (1/2) + (1/342) - (217/18)
C₂ = (20619 - 1 + 6 - 819)/(342)
C₂ = 19805/342
Therefore, the solution to the differential equation y''(t) = 1 - t^17 with initial condition y(1) = 12 is:
y(t) = (1/2)t^2 - (1/342)t^19 + (217/18)t + (19805/342)
None of the provided options (a, b, c, d) match the correct solution.
Learn more about equation here:
https://brainly.com/question/10724260
#SPJ11
Polynomial uing Remainder Theorem and Factor Theorem checking uing ynthetic diviion. X^4 - x^3 - 3x^2 4x 2 ÷ (x 2)
Answers
The remainder of the polynomial using the remainder theorem and factor theorem is 6.
Apply the remainder theorem,
When we divide a polynomial
f(x) by (x − c)
f(x) = (x − c)q(x) + r
f(c) = 0 + r
Here,
f(x)=(x−c)q(x)+rf(c)=0+r
and (x−c) is (x−(−2))
Therefore,
f(−2) = \((-2)^{4} - (-2)^3 - 3(-2)^2 + 4(-2) + 2\)
= 16 + 8 − 12 − 8 + 2
= 6
Hence, the remainder of the polynomial using the remainder theorem is 6.
Whereas using the factor theorem and doing synthetic division, we get,
x = -2 is a zero of f(x), and x+2 is a factor of f(x). To factor f(x), we divide
the coefficients of the polynomial as follows -
-2 | 1 -1 -3 4 2
-2 6 -6 4
-----------------------------------------
1 -3 3 -2 6
Hence, we get that 6 is the remainder when (\(x^4-x^3-3x^2+4x+2\)) ÷ (x+2), using the factor theorem.
Read more about factor theorem:
brainly.com/question/19030198
#SPJ4
The complete question is -
Find the remainder using the Remainder Theorem and Factor Theorem using the synthetic division of the given polynomial, \(x^4-x^3-3x^2+4x+2\) ÷ (x+2)
Factor the expression 4x^2 - 12x - 7
Answers
Answer:
(2x+1) (2x-7)
Step-by-step explanation:
Multiply the coefficient of the first term by the constant 4 • -7 = -28
Find two factors of -28 whose sum equals the coefficient of the middle term, which is -12
( -28 + 1 = -27
-14 + 2 = -12 )
Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, -14 and 2
4x2 - 14x + 2x - 7
Add up the first 2 terms, pulling out like factors :
2x • (2x-7)
Add up the last 2 terms, pulling out common factors :
1 • (2x-7)
Add up the four terms :
(2x+1) • (2x-7)
Point A is (2,-1) and Point B is (4,3)
(2,-1),(4.3) find the distance
Answers
The distance of AB is 2√5.
Given that the point A is (2,-1) and point B is (4,3).
The distance formula gives us the shortest distance between the given two points in a plane of two dimensional.
The given points is point A(x₁,y₁)=(2,-1) and point B (x₂,y₂)=(4,3).
Now, we will use the distance formula to calculate the distance that is D=√(x₂-x₁)²+(y₂-y₁)².
Further, we will substitute the given values in the above formula, we get
D=√(4-2)²+(3-(-1))²
D=√2²+(3+1)²
D=√2²+4²
D=√4+16
D=√20
D=2√5
Hence, the distance of AB from the given points point A is (2,-1) and point B is (4,3) is 2√5.
Learn more about the distance formula from here brainly.com/question/1872885
#SPJ9
5x−2(x+1)=1/4 find x pretty please
Answers
Answer:
Delaney solve for X by isolating it, or getting it by it self
Step-by-step explanation:
5x−2(x+1)=1/4 (distribute the 2)
5x-2x - 2 = 1/4 (subtract 2x from 5x)
3x -2 +2 = 1/4 +2 (add 2 to both sides)
3x = 2_1/4 (put 2 & 1/4 together)
3x = 9/4 (convert 2_1/4 to 9/4)
\(\frac{1}{3}\)*3*x = \(\frac{1}{3}\)*\(\frac{9}{4}\) ( mutilply both sides by 1/3)
X = 3/4 (cross multiply )
There you go
X = \(\frac{3}{4}\)
Answer:
\(\huge\boxed{\bf\:x = \frac{3}{4}}\)
Step-by-step explanation:
\(5x - 2(x+1)=\frac{1}{4}\)
Use the distributive property for 2(x + 1).
\(5x - 2x - 2= \frac{1}{4}\)
Subtract 2x from 5x.
\(3x - 2= \frac{1}{4}\)
Bring 2 to the right hand side of the equation .
\(3x = \frac{1}{4} + 2\)
Add 1/4 & 2.
\(3x = \frac{1}{4} + \frac{8}{4} \: \: [LCM = 4]\\3x = \frac{9}{4}\)
Now, bring 3 to the right hand side of the equation .
\(x = \frac{9}{4} \times \frac{1}{3}\\x = \frac{9}{12}\\\boxed{\bf\:x = \frac{3}{4}}\)
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
traffic engineers in florida want to reduce the rate of accidents between pedestrians and cars at intersections. research has shown that replacing stoplights with roundabouts (also called traffic circles) can improve safety for bikers and pedestrians. engineers wanted to test this concept so it can be applied across florida, and last year, they replaced five timed stoplights in a florida city with roundabouts. the accident rates at five intersections before the intervention were 5.1, 3.4, 6.1, 4.9, and 4.1 accidents per month. after installing roundabouts, the new rates of pedestrian accidents were 4.5, 3.6, 5.5, 4.8, and 4.1 accidents per month. does replacing stoplights with roundabouts significantly reduce the rate of accidents at intersections? use an alpha value of 0.05 in your decision.
Answers
Replacing stoplights with roundabouts does not significantly reduce the rate of accidents at intersections based on the given data.
Based on the statistical analysis, replacing stoplights with roundabouts does not significantly reduce the rate of accidents at intersections.
To test this hypothesis, we will use a paired t-test, which compares the means of two sets of paired data. The null hypothesis is that there is no significant difference between the mean accident rates before and after installing roundabouts, while the alternative hypothesis is that the mean accident rate after installing roundabouts is significantly lower than before.
Here are the steps to conduct the paired t-test:
Calculate the difference between the accident rates before and after installing roundabouts for each intersection.Calculate the mean and standard deviation of the differences.Calculate the t-value using the formula: t = (mean of the differences) / (standard deviation of the differences / sqrt(n)), where n is the number of paired observations.Calculate the degrees of freedom using the formula: df = n - 1.Find the critical t-value at a 0.05 level of significance and df from a t-distribution table.Compare the calculated t-value with the critical t-value. If the calculated t-value is greater than the critical t-value, reject the null hypothesis. If the calculated t-value is less than or equal to the critical t-value, fail to reject the null hypothesis.Using the given data, the differences between the accident rates before and after installing roundabouts are:
-0.6, 0.2, 0.6, -0.1, 0
The mean of the differences is 0.02, and the standard deviation is 0.43. There are 5 paired observations, so the degrees of freedom are 4.
Using the formula, we get:
t = 0.02 / (0.43 / √(5)) = 0.14
The critical t-value at a 0.05 level of significance and 4 degrees of freedom is 2.776 from a t-distribution table.
Since the calculated t-value (0.14) is less than the critical t-value (2.776), we fail to reject the null hypothesis. Therefore, we can conclude that replacing stoplights with roundabouts does not significantly reduce the rate of accidents at intersections based on the given data.
Learn more about the null hypothesis
https://brainly.com/question/25263462
#SPJ4
What is the value of the angle marked with x?

Answers
Answer:
87
Step-by-step explanation:
Answer:
x=91
Step-by-step explanation:
All angles of a quadrilateral can add up to 360.
360-87=273
273/3=91
x=91
I am not to sure, but I think this is the answer.
The marginal-cost function for a product is dc/dq = 1/3-1/2√3q. If c(0) = 100 then the cost of producing 300 unit is
Answers
Given information: Marginal-cost function is dc/dq = 1/3-1/2√3q, c(0) = 100To find: The cost of producing 300 unit.
To find the cost of producing 300 units, we need to integrate the marginal-cost function.∫dc/dq dq = ∫(1/3 - 1/2√3q)dqOn integrating, we get,c(q) = q/3 - √3q²/4 + C, where C is the constant of integration.To find the value of C, we will use the given condition: c(0) = 100c(0) = 0/3 - √3(0)²/4 + C = 100C = 100So, the cost function is:c(q) = q/3 - √3q²/4 + 100The cost of producing 300 units will be:c(300) = (300/3) - √3(300)²/4 + 100= 100 - 225√3 + 300= 400 - 225√3Therefore, the cost of producing 300 units is 400 - 225√3. Answer: 400 - 225√3.
To know more about cost of producing visit:
https://brainly.com/question/31444839
#SPJ11
The correct answer of the marginal-cost function for a product is cost of producing 300 units is 100.
The marginal-cost function for a product is dc/dq = 1/3-1/2√3q.
Cost of producing 300 unit is to be determined.
The marginal-cost function is given as,dc/dq = 1/3 - (1/2) √3q
Integrate dc/dq to get the cost function c(q),c(q) = ∫dc/dq dqc(q) = ∫(1/3 - (1/2) √3q) dqc(q) = (1/3)q - (1/4) √3q^2 + k
where k is the constant of integration.
To find the value of k, use the given condition that c(0) = 100c(q) = (1/3)q - (1/4) √3q^2 + 100When q = 0,c(0) = (1/3)(0) - (1/4) √3(0)^2 + 100c(0) = 100
Therefore, k = 100
Thus, the cost function isc(q) = (1/3)q - (1/4) √3q^2 + 100
The cost of producing 300 units is
c(300)c(300) = (1/3)(300) - (1/4) √3(300)^2 + 100c(300) = 100
Therefore, the cost of producing 300 units is 100 units.
To know more about function,visit:
https://brainly.com/question/30721594
#SPJ11
A summary of data that shows the number of observations in each of several nonoverlapping bins is called a(n) _____.
Answers
A summary of data that shows the number of observations in each of several non-overlapping bins is called a histogram.
A histogram is a graph used to visualize the distribution of a dataset. The x-axis represents the different ranges of the data being observed, which are usually called bins. The y-axis displays the frequency or count of data values that fall into each bin.
The shape of a histogram can provide valuable insights into the underlying data distribution. For example, if a histogram is bell-shaped, it indicates that the data follows a normal distribution, which is a symmetrical distribution with most values clustered around the mean. If a histogram is skewed to the left, the data has a long tail on the left-hand side and is concentrated on the right-hand side. If a histogram is skewed to the right, the data has a long tail on the right-hand side and is concentrated on the left-hand side. In conclusion, a histogram is a useful tool for summarizing data and providing insights into its distribution.
Know more about histogram here:
https://brainly.com/question/16819077
#SPJ11
Andrew invested $3,100 in an account paying an interest rate of 2. 1% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest dollar, would be in the account after 16 years?.
Answers
Answer: 4,322.883
Step-by-step explanation:
Assuming that the interest rate is per year:
4,322.883
Throw n balls into m bins, where m and n are positive integers. Let X be the number of bins with exactly one ball. Compute varX.
Answers
By using the formula for variance
\(varX= m*(n*(m-1)/m^n)(1 - n(m-1)/(m^n-1))\)
To compute varX:
we first need to find the expected value of X, denoted as E(X).
We can approach this by using the linearity of expectation, which states that the expected value of the sum of random variables is equal to the sum of their individual expected values.
Let's define a random variable Xi as the number of bins with exactly one ball. Then, we have:
\(X = X1 + X2 + ... + Xm\)
where m is the total number of bins.
By the definition of Xi, we know that Xi can only take on values between 0 and 1, since a bin can either have exactly one ball (Xi = 1) or not (Xi = 0).
To find E(Xi), we can use the probability of Xi being 1. The probability that a specific bin has exactly one ball is given by:
\(P(Xi = 1) = (n choose 1) * ((m-1) choose (n-1)) / (m choose n)\)
The first term (n choose 1) represents the number of ways to choose one ball out of n balls to put into the bin. The second term ((m-1) choose (n-1)) represents the number of ways to choose (n-1) balls out of the remaining (m-1) bins. Dividing by (m choose n) gives us the probability that exactly one bin has one ball.
Therefore, we have:
E(Xi) = P(Xi = 1) * 1 + P(Xi = 0) * 0
= P(Xi = 1)=\((n choose 1) * ((m-1) choose (n-1)) / (m choose n)\)
Using the linearity of expectation, we can find E(X) as:
E(X) = E(X1) + E(X2) + ... + E(Xm)
= \(m * (n choose 1) * ((m-1) choose (n-1)) / (m choose n)\)
Now, to find varX, we need to find the variance of Xi and use the formula for variance of a sum of random variables.
The variance of Xi can be found as:
Var(Xi) = E(Xi^2) - (E(Xi))^2
Since Xi can only take on values 0 or 1, we have:
E(Xi^2) =\(0^2 * P(Xi = 0) + 1^2 * P(Xi = 1) = P(Xi = 1)\)
Therefore, we have:
Var(Xi) = P(Xi = 1) - (E(Xi))^2
= \(m*(n*(m-1)/m^n) + m*(m-1)(n(m-1)/m^n)^2 - (mn(m-1)/m^n)^2\)
Using the formula for variance of a sum of random variables, we have:
varX = Var(X1 + X2 + ... + Xm)
= Var(X1) + Var(X2) + ... + Var(Xm) (since Xi's are independent)
= \(m*(n*(m-1)/m^n)(1 - n(m-1)/(m^n-1))\)
To know more about Formula of Variance:
https://brainly.com/question/20066860
#SPJ11
solve the inequality $\frac{29}{289z<\frac{16}{161}z$. try to solve the problem without doing a lot of messy computations!
Answers
The solution to the given inequality as represented in the task content are; z < - 1.00485413 OR z > 1.00485413.
What is the solution to the given inequality?It follows from the task content that the solution of the given inequality; ( 29 / 289z ) < ( 16 / 161 ) z is to be determined.
Since the given inequality is;
( 29 / 289z ) < ( 16 / 161 ) z
By cross multiplication; we have;
161 × 29 < ( 16z × 289z )
( 161 × 29 ) / ( 16 × 289 ) < z²
1.00973183 < z²
Therefore;
1.00485413 < z. OR. -1.00485413 > z.
Ultimately, z < - 1.00485413 OR z > 1.00485413.
Read more on inequalities;
https://brainly.com/question/25275758
#SPJ1
Which table can be created using the equation below? –2 + 4x = y A 2-column table with 3 rows. Column 1 is labeled x with entries negative 5, 0, 3. Column 2 is labeled y with entries negative 22, negative 2, 10. A 2-column table with 3 rows. Column 1 is labeled x with entries negative 22, negative 2, 10. Column 2 is labeled y with entries negative 5, 0, 3. A 2-column table with 3 rows. Column 1 is labeled x with entries negative 5, 0, 3. Column 2 is labeled y with entries negative 18, negative 2, 10. A 2-column table with 3 rows. Column 1 is labeled x with entries negative 18, negative 2, 10. Column 2 is labeled y with entries negative 5, 0, 3.
Answers
The correct answer is C. A 2-column table with 3 rows. Column 1 is labeled x with entries negative 5, 0, 3. Column 2 is labeled y with entries negative 18, negative 2, 10.
Explanation:
The purpose of an equation is to show the equivalence between two mathematical expressions. This implies in the equation "–2 + 4x = y" the value of y should always be the same that -2 + 4x. Additionally, if a table is created with different values of x and y the equivalence should always be true. This occurs only in the third option.
x y
5 -18
0 -2
3 10
First row:
-2 + 4 (5) = y (5 is the value of x which is first multyply by 4)
-2 + 20 = -18 (value of y in the table)
Second row:
-2 + 4 (0) y
-2 + 0 = -2
Third row:
-2 + 4 (3) = y
-2 + 12 = 10
Answer:
it is c
Step-by-step explanation:
Two parallel lines l and m are cut by a transversal t. If the interior angles of the same side of t are (2x−8)∘ and (3x−7)∘, find the measure of each of these angles.
Answers
Step-by-step explanation:
When two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary. This means that their measures add up to 180 degrees.
In this case, the two interior angles on the same side of the transversal 't' are (2x-8) degrees and (3x-7) degrees. Since these angles are supplementary, we can write the equation (2x-8) + (3x-7) = 180.
Solving this equation for x, we get:
(2x-8) + (3x-7) = 180
5x - 15 = 180
5x = 195
x = 39
Substituting this value of x into the expressions for the two interior angles, we find that their measures are:
(2x-8) = (2*39 - 8) = 70 degrees
(3x-7) = (3*39 - 7) = 110 degrees
So, the measure of each of these angles is 70 degrees and 110 degrees.
maths question please help !! thank u :)

Answers
Answer:
1350m
Step-by-step explanation:
Let the distance ran by Denise, Farah and Elaine be D, F and E meters respectively.
From the given information,
D= ⅔(E +F) -----(1)
E= ½(D +F) -----(2)
Let's get rid of the fraction so the equations are much easier to work with.
From (1):
3D= 2(E +F) (Multiply both sides by 3)
3D= 2E +2F -----(3) (Expand)
From (2):
2E= D +F -----(4)
Substitute (4) into (3):
3D= D +F +2F
3D -D= 3F
2D= 3F
Given that Farah ran 360m, F= 360.
2D= 3(360)
2D= 1080
D= 1080 ÷2
D= 540
2E= D +F
2E= 540 +360
2E= 900
E= 900 ÷2
E= 450
Total distance the 3 girls ran
= D +F +E
= 540 +360 +450
= 1350m
Alternatively, you could start by substituting F= 360 to equations (1) and (2).
Jen and Holly are on the Athletic council and want to put a blow up version on the school mascot in the parking lot. They need to tie it down.
Jen’s rope is 7.8 m long and makes an angle of 360 with the ground. Holly’s rope is 5.9 m long. The wind is really strong so they will secure both ropes to the left of the mascot. How far to the nearest tenth of a metre, is Jen from Holly?
Answers
Answer:
2.6 m
Step-by-step explanation:
In the attached diagram
Consider Triangle ABC
\(\sin36^\circ =\dfrac{|BC|}{7.8} \\|BC|=7.8*\sin36^\circ\\|BC|=4.5847$ m\)
Our goal is to determine the distance of Jen (at point A) to Holly (at Point D).
In Triangle ABC
\(\cos 36^\circ =\dfrac{|AC|}{7.8} \\|AC|=7.8*\cos36^\circ\\|AC|=6.3103$ m\)
In Triangle BDC
Applying Pythagoras Theorem
\(|BD|^2=|BC|^2+|CD|^2\\5.9^2=4.5847^2+|CD|^2\\|CD|^2=5.9^2-4.5847^2\\|CD|^2=13.7905\\|CD|=\sqrt{13.7905}=3.7136$ m\)
Now, |AC|=|AD|+|DC|
6.3103=|AD|+3.7136
|AD|=6.3103-3.7136
|AD|=2.5967
|AD|=2.6m (correct to the nearest tenth of a metre)
The distance of Jen from Holly is 2.6m.

Which numerical expression provides the solution to the equation 7x2 + 4x – 8 = 14?

Answers
Answer:
The answer is C
Step-by-step explanation:
Answer:
The answer is D
Step-by-step explanation:
-4^2-4(7)(-8) = 240
answer the following, Round final answer to 4 decimal places. a.) Which of the following is the correct wording for the randon variable? r×= the percentage of all people in favor of a new building project rv= the number of people who are in favor of a new building project r N= the number of people polled r×= the number of people out of 10 who are in favor of a new building project b.) What is the probability that exactly 4 of them favor the new building project? c.) What is the probabilitv that less than 4 of them favor the new building project? d.) What is the probabilitv that more than 4 of them favor the new building project? e.) What is the probabilitv that exactly 6 of them favor the new building project? f.) What is the probability that at least 6 of them favor the new building project? 8.) What is the probabilitv that at most 6 of them favor the new building project?
Answers
In this problem, we are dealing with a random variable related to people's opinions on a new building project. We are given four options for the correct wording of the random variable and need to determine the correct one. Additionally, we are asked to calculate probabilities associated with the number of people who favor the new building project, ranging from exactly 4 to at most 6.
a) The correct wording for the random variable is "rv = the number of people who are in favor of a new building project." This wording accurately represents the random variable as the count of individuals who support the project.
b) To calculate the probability that exactly 4 people favor the new building project, we need to use the binomial probability formula. Assuming the probability of a person favoring the project is p, we can calculate P(X = 4) = (number of ways to choose 4 out of 10) * (p^4) * ((1-p)^(10-4)). The value of p is not given in the problem, so this calculation requires additional information.
c) To find the probability that less than 4 people favor the new building project, we can calculate P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3). Again, the value of p is needed to perform the calculations.
d) The probability that more than 4 people favor the new building project can be calculated as P(X > 4) = 1 - P(X ≤ 4) = 1 - (P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)).
e) The probability that exactly 6 people favor the new building project can be calculated as P(X = 6) using the binomial probability formula.
f) To find the probability that at least 6 people favor the new building project, we can calculate P(X ≥ 6) = P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10).
g) Finally, to determine the probability that at most 6 people favor the new building project, we can calculate P(X ≤ 6) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6).
To learn more about Binomial probability - brainly.com/question/12474772
#SPJ11
Consider the function f(x,y) = 8x3 + y3 - 6xy + 2 a.) Find the critical points of the function. b.) Use the Second Derivative Test to classify each critical point as a local maximum, local minimum, or a saddle point.
Answers
The critical points are (0, 0) and (1/2, 1/8).
To find the critical points of the function f(x, y) = 8x^3 + y^3 - 6xy + 2, we need to find the points where the partial derivatives of f with respect to x and y are equal to zero.
a.) Finding the critical points:
∂f/∂x = 24x^2 - 6y = 0
∂f/∂y = 3y^2 - 6x = 0
From the first equation, we have:
24x^2 - 6y = 0
4x^2 - y = 0
y = 4x^2
Substituting y = 4x^2 into the second equation:
3(4x^2)^2 - 6x = 0
48x^4 - 6x = 0
6x(8x^3 - 1) = 0
This gives two possible cases:
6x = 0, which implies x = 0.
8x^3 - 1 = 0, which implies 8x^3 = 1 and x^3 = 1/8. Solving this equation, we find x = 1/2.
For x = 0, we can substitute it back into y = 4x^2 to find y = 0.
So, the critical points are (0, 0) and (1/2, 1/8).
To know more about critical points refer here:
https://brainly.com/question/32077588
#SPJ11
In a fifth-grade class, 3/4 of the students like to go to the movies. Of the students who like to go to the movies, 2/3 of them like action movies. What fraction of the students in the class like to go to action movies
Answers
Answer:
1/2 of the class
give brainliest if it helps

Find y as a function of x if y′′′−17y′′+72y′=168e^x, y(0)=16, y′(0)=23, y′′(0)=24.
Answers
The function is :\(y(x) = 10 + (7/8) e^8x + (97/72) e^9x + 3 e^x\)
To find y as a function of x, we need to solve the differential equation:
\(y′′′ − 17y′′ + 72y′ = 168e^x\)
Step 1: Find the characteristic equation
\(r^3 - 17r^2 + 72r = 0\)
Factor out r:
\(r(r^2 - 17r + 72) = 0\)
Factor the quadratic:
r(r - 8)(r - 9) = 0
So the roots are:
r₁ = 0, r₂ = 8, r₃ = 9
Step 2: Find the general solution
The general solution will be of the form:
\(y(x) = C1 + C2e^8x + C3e^9x + y_p(x)\)
where y_p(x) is a particular solution to the non-homogeneous equation.
Step 3: Find the particular solution
We can use the method of undetermined coefficients to find a particular solution. Since the right-hand side is an exponential function, we can guess that the particular solution is also an exponential function:
\(y_p(x) = A e^x\)
\(y_p′(x) = A e^x\)
\(y_p′′(x) = A e^x\)
\(y_p′′′(x) = A e^x\)
Substituting into the differential equation:
\(A e^x - 17A e^x + 72A e^x = 168 e^x\)
Simplifying:
\(56A e^x = 168 e^x\)
A = 3
So the particular solution is:
\(y_p(x) = 3 e^x\)
Step 4: Find the constants using initial conditions
y(0) = C₁ + C₂ + C₃ + 3 = 16
y′(0) = 8C₂ + 9C₃ + 3 = 23
\(y′′(0) = 8^2 C2 + 9^2 C3 = 24\)
Solving for the constants, we get:
C₁ = 10, C₂ = 7/8, C₃ = 97/72
Step 5: Write the final solution
Substituting the constants and the particular solution into the general solution, we get:
\(y(x) = 10 + (7/8) e^8x + (97/72) e^9x + 3 e^x\)
So the function y(x) is:
\(y(x) = 10 + (7/8) e^8x + (97/72) e^9x + 3 e^x\)
To learn more about the differential equation,
https://brainly.com/question/31583235
#SPJ4
Solve for g.
2(g - 13) = 12
g
Answers
Answer:
-2
Step-by-step explanation:
Please help me i really need help. you get 49+ pts
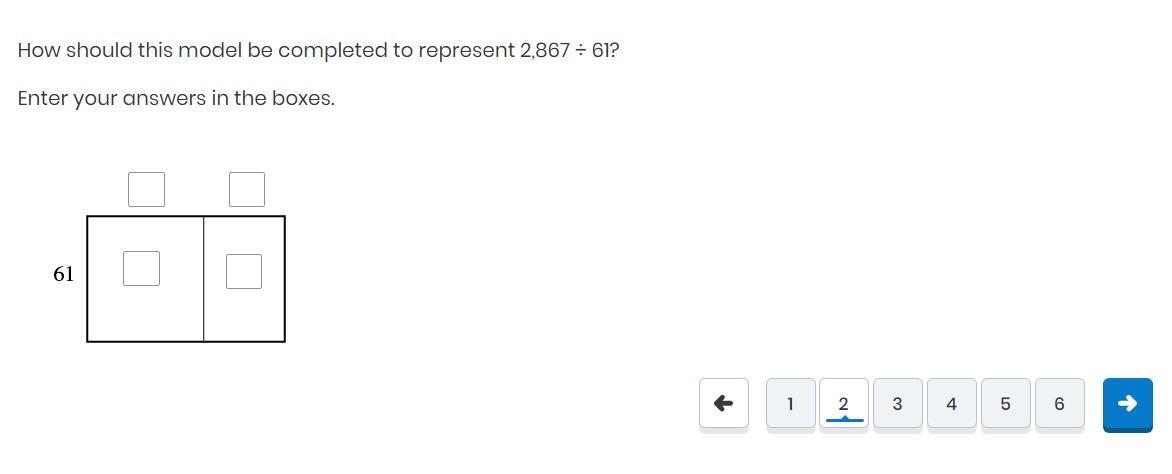

Answers
Answer:For the first one i only know the answer to the division problem i don't know how to do the box things but the division problem is 2,867 divided by 61=47 with no remainder.
The second one is 3,353 divided by 75 =40 R 4
What is the solution set for 10(1−x)<−2x−6 ?
I'll give brainliest for right answer.
Answers
Answer:
x>2
Step-by-step explanation:
10(1-x) <-2x-6
10-10x<-2x-6
10-10x +2x<-6
-8x<-6-10
-8x<-16 (divide both sides)
x>2
Answer:
x>2
Step-by-step explanation:
1) 10-10x<-2x-6
2)10-10x-10<-2x-6-10
3) -10x<-2x-16
4)-10x+2x<-2x-16+2x
5) -8x<-16
6) (-8x)(-1)>(-16)(-1)
7) 8x>16
8) x>2
\(\frac{\frac{1}{x}+ \frac{2}{x^{2} } }{x+\frac{8}{x^{2} } }\)
Answers
Answer:
\( \frac{x + 2}{x {}^{3} + 8} \)
Step-by-step explanation:
\( \frac{ \frac{1}{x} + \frac{2}{x {}^{2} } }{x + \frac{8}{x {}^{2} } } \)
\( \frac{ \frac{x + 2}{x {}^{2} } }{ \frac{x {}^{3} + 8 }{x {}^{2} } } \)
\( \frac{x + 2}{x {}^{3} + 8 } \)
Consider a sample with data values of 27, 25, 20, 15, 30, 34, 28, and 25. Compute the 21st, 26th, 65th, and 75th percentiles. If needed, round your answers to two decimal digits. Percentile Value 21% 26% 65% 75%
Answers
The the 21st, 26th, 65th, and 75th percentiles are 19.45, 21.7, 27.85, and 29.50.
How to compute the percentile?Here, n=8
P21=(21(n+1)100)th value of the observation
=(21⋅9/100)th value of the observation
=1st observation +0.89[2nd-1st]
=15+0.89[20-15
= 19.45
P26 = (26(n+1)100)th value of the observation
=(26⋅9/100)th value of the observation
=2nd observation +0.34[3rd-2nd]
=20+0.34[25-20]
=20+0.34(5)
= 21.7
P65= (65(n+1)100)th value of the observation
=(65⋅9/100)th value of the observation
=5th observation +0.85[6th-5th]
=27+0.85[28-27
= 27.85
P75 = (75(n+1)100)th value of the observation
=(75⋅9/100)th value of the observation
6th observation +0.75[7th-6th]
=28+0.75[30-28]
= 28 + 1.50
= 29.50
Learn more about samples on:
https://brainly.com/question/17831271
#SPJ1
Suppose the coverage score on a national test is 500 with a standard deviation of 100. if each score is increased by 25, what are the new mean and standard deviation?
Answers
The new man's age would be 525, however the standard deviation would remain the same.
What is standard deviation?The Standard Deviation measures how evenly distributed numbers are. It has the sign (a Greek letter sigma) and the calculation is simple: it's the variance as a square root.
The average national test score is 500, for a standard deviation = 100.
Each score has been boosted by 25 points.
Let y = x + 25
where x is the old mean & y is the new score
E(x) = 500 and standard deviation (x) = 100 (given)
E(y) = E(x + 25)
= E(x) + 25
= 500 + 25
= 525
Variable (y) = Variable (x + 25)
= Variable (x)
As, √variance y = √variance x
standard deviation(y) = standard deviation(x)
= 100
Therefore, the new standard deviation is same as the old one.
To know more about standard deviation, here
https://brainly.com/question/26941429
#SPJ4
trigonometry, please help thanks

Answers
Answer:
x = 3.25 m
Step-by-step explanation:
First, find the height of the triangle using sin31:
sin 31 = h/9 ---> h = 9sin31 = 4.64 m
Next, we can now solve for x using tan55:
tan 55 = h/x --> x = (4.64 m)/(tan 55) = 3.25 m
What is y = x2 + 4x -2? I need help
Answers
Answer: (−2,−6) Focus: (−2,−234) Axis of Symmetry: x=−2 Directrix: y=−254x
Step-by-step explanation: it different ways to answer so i just give you all of them
Answer:
9 = -254x
Step-by-step explanation:
I did the test
Hope this helps :)