Answers
Answer:
x = 8
Step-by-step explanation:
You know that 7x - 4 and 5x + 12 are equal, so you can set up an equation and solve it:
\(7x - 5 = 5x + 12\)
subtract 5x from both sides
\(2x-4=12\)
Add 4 to both sides
\(2x = 16\)
divide both sides by 2
\(x = 8\)
Answer:
7x - 4......1
5х + 12......2
on multiplying by 3 in eq 1
= 21x-12...3
on substracting eq 2 from 3
21x-12=0
-5x+12=0
=16x=0
x=1/16
sorry but I can't find your answer
but I tried...
Related Questions
Please help!! I’m having lots of trouble

Answers
x=4/tan(20)
Make sure your calculator is in degree mode
In ANOVA, the independent variable is ______ with 2 or more levels and the dependent variable is _______
a. interval/ratio with 2 or more levels; nominal
b. nominal with 2 or more levels; interval/ratio
c. ordinal with 2 or more levels, nominal
d. interval/ratio, nominal with 2 or more levels
Answers
The correct option is (d) interval/ratio, nominal with 2 or more levels.
In ANOVA (Analysis of Variance), the independent variable is interval/ratio with 2 or more levels, and the dependent variable is nominal with 2 or more levels. Here, ANOVA is a statistical tool that is used to analyze the significant differences between two or more group means.
ANOVA is a statistical test that helps to compare the means of three or more samples by analyzing the variance among them. It is used when there are more than two groups to compare. It is an extension of the t-test, which is used for comparing the means of two groups.
The ANOVA test has three types:One-way ANOVA: Compares the means of one independent variable with a single factor.Two-way ANOVA: Compares the means of two independent variables with more than one factor.Multi-way ANOVA: Compares the means of three or more independent variables with more than one factor.
The ANOVA test is based on the F-test, which measures the ratio of the variation between the group means to the variation within the groups. If the calculated F-value is larger than the critical F-value, then the null hypothesis is rejected, which implies that there are significant differences between the group means.
To know more about independent visit:
https://brainly.com/question/27765350
#SPJ11
The legal maximum speed on UK motorways is 70 miles per hour.
Work out the legal maximum speed on UK motorways in metres
per second (m/s).
Give your answer to the nearest whole number
Answers
Answer: 31 m/s
Step-by-step explanation:
70 miles per hour = 112654 meters per 3600 seconds = 31.3 = 31 m/s
1) (3x-5)^2
2) (3xy-1/3)^2
Answers
1)
=(3x)² - 2 × 3x × 5+5²
=3²x²2 × 3x × 5+5²
=9x² -2 × 3x × 5 + 5²
=9x² -2 x 3x x 5 + 25
=9x²30x + 25
explain why
a negative divided by a negative is a positive
Answers
Answer:
it's law
Step-by-step explanation:
i think it is law of mathematics. isn't it?
A card is randomly chosen from the cards in the image. Find the probability of choosing the cards with either Q or R on them.
P(Q or R) = ________

Answers
The probability of choosing cards either Q or R when a card is drawn from a deck of 8 cards is 0.25.
Given that a card is randomly chosen from 8 cards shown in figure.
We have to calculate the probability of choosing either Q or R when a card is drawn from those 8 cards.
Probability means calculating the likeliness of happening an event among all the events possible. It lies between 0 and 1. It cannot be negative.
Number of cards=8
Number of repeated cards=0
Number of cards showing Q and R =1 each.
Probability of getting Q or R is P(X=Q)+P(X=R)
= 1/8+1/8
=2/8
=1/4
=0.25
Hence the probability of getting either P or Q when a card is drawn from 8 cards is 0.25.
Learn more about probability at https://brainly.com/question/24756209
#SPJ1
Please help me with this :)

Answers
Answer: its A ........................22 +/- (3(4)/sqrt 144) = 22 +/- 1 = 21 - 23
Step-by-step explanation:
Answer:
i wanna say A srry if im wrong tho im never right
Step-by-step explanation:
ye

1) A tv has a sale price of $450 and has a sales tax of 6% Find the total price.
Sales tax:
Total price:
Answers
Answer:
Sales tax : $27
Total price : $477
Step-by-step explanation:
Given that:
Sale price of tv = $450
Sales tax = 6%
Amount of sales tax = \(\frac{6}{100}*450\)
Amount of sales tax = 0.06 * 450
Amount of sales tax = $27
Total price = Sale price + Sales tax
Total price = 450 + 27 = $477
Hence,
Sales tax : $27
Total price : $477
Given: ∆MNP, PM = 8 m∠P = 90°, m∠N = 58° Find: Perimeter of ∆MNP
(Not 22.4 or 22.43)
Please answer ASAP, brainly awarded.
Answers
Answer:
Step-by-step explanation:
Triangle MNP is a right triangle with the following values:
m∠P = 90°m∠N = 58°PM = 8Interior angles of a triangle sum to 180°. Therefore:
m∠M + m∠N + m∠P = 180°
m∠M + 58° + 90° = 180°
m∠M + 148° = 180°
m∠M = 32°
To find the measures of sides MN and NP, use the Law of Sines:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Substitute the values into the formula:
\(\dfrac{MN}{\sin P}=\dfrac{NP}{\sin M}=\dfrac{PM}{\sin N}\)
\(\dfrac{MN}{\sin 90^{\circ}}=\dfrac{NP}{\sin 32^{\circ}}=\dfrac{8}{\sin 58^{\circ}}\)
Therefore:
\(MN=\dfrac{8\sin 90^{\circ}}{\sin 58^{\circ}}=9.43342722...\)
\(NP=\dfrac{8\sin 32^{\circ}}{\sin 58^{\circ}}=4.99895481...\)
To find the perimeter of triangle MNP, sum the lengths of the sides.
\(\begin{aligned}\textsf{Perimeter}&=MN+NP+PM\\&=9.43342722...+4.99895481...+8\\&=22.4323820...\\&=22.43\; \sf units\; (2\;d.p.)\end{aligned}\)

find the highest common factor of 9, 12 and 15
Answers
Hello there! :)
The highest common factor of 9, 12, and 15 is 3.
To find the HCF (also called the GCF) of two or more numbers, we list their factors:
9: 1, 3, 9
12: 1, 2, 3, 4, 6, 12
15: 1, 3, 5, 15
Can you see that 3 is their GCF?
Hope this helps!
~Just a determined gal
#CarryOnLearning
\(MysteriousNature\)
what is the value of the 5th term

Answers
First term (a1) = -7
Second term (a2) = -2
Common difference: a2 - a1 = -2-(-7) = 5
Hence, Fifth term = a1 + 4d = -7 + 4(5) = 13
Evaluate and reduce:
-4/7•9
Answers
Answer:
119/100.
Step-by-step explanation:
7.9 means In fraction form 790/ 100
4÷790/100
use LCM method the LCM of 4 and 100 is 100 so,100÷1=100*4=400
100÷100=1*790=790
400+790/100=1190/100( one zero is cancel out with one zero.
the final answer 119/100.
The diagram below shows part of the graph of the equation y=\(2x^{2}+ax+b.\) the graph intersects the x-axis at the points \((-\frac{7}{2}, 0) and (2,0)\). Find the value of a and the value of b
![The diagram below shows part of the graph of the equation y=[tex]2x^{2}+ax+b.[/tex] the graph intersects](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/YwYLuW7uDWzWPsV7UUhm0V4pOGEqefU9.jpeg)
Answers
The value of a is 3.
The value of b is -14.
What is Coordinates?
A pair of numbers which describe the exact position of a point on a cartesian plane by using the horizontal and vertical lines is called the coordinates.
Given that;
The function of the graph is,
y = 2x² + ax + b
The graph intersects the x-axis at the points (-7/2, 0) and (2, 0).
Now,
Since, The graph intersects the x-axis at the points (-7/2, 0) and (2, 0).
Hence, The points must satisfy the graph of the function.
So, Points (-7/2, 0) and (2, 0) are satisfy the function y = 2x² + ax + b.
When point (-7/2, 0) satisfy the function y = 2x² + ax + b
Then,
0 = 2 × (-7/2)² + a × (-7/2) + b
0 = 49/2 - 7a/2 + b
7a/2 - b = 49/2 .... (i)
And, When point (2, 0) satisfy the function y = 2x² + ax + b
Then,
0 = 2 × (2)² + a×2 + b
2a + b = -8 .... (ii)
Add equation (i) and (ii) we get;
7a/2 - b + 2a - b = 49/2 + (-8)
11a/2 = 33/2
11a = 33
a = 3
And, 2a + b = -8
2 × 3 + b = -8
b = -8 - 6
b = -14
Hence, The value of a is 3.
The value of b is -14.
Learn more about the coordinate visit:
https://brainly.com/question/12959377
#SPJ1
let u={12,13, 14,15,16 ,17,18} and a={12, 14, 15, 18}. find a the roster method to write the set A'. A' = (Use a comma to separate answers as needed.)
Answers
The roster method to write the set A' as {13, 16, 17}.
- "Set" is a collection of distinct objects, which can be numbers or other elements.
- "Roster method" is a way of listing all the elements in a set by separating them with commas and enclosing them within braces { }.
Now, let's find set A', which is the complement of set A with respect to set U. This means that A' contains all the elements in U that are not in A.
U = {12, 13, 14, 15, 16, 17, 18}
A = {12, 14, 15, 18}
To find A', we will list the elements from set U that are not in set A:
A' = {13, 16, 17}
So, using the roster method, the complement of set A (A') is written as:
A' = {13, 16, 17}
In summary, the roster method is useful for listing all the elements in a set. By finding the complement of set A with respect to set U, we can use the roster method to write the set A' as {13, 16, 17}.
Learn more about Set here:
https://brainly.com/question/8053622
#SPJ11
Consider the following.sum n = 1 to [infinity] n ^ 2 * (3/8) ^ n (a) Verify that the series converges.
lim eta infinity | partial n + 1 partial n |=
Answers
To determine the convergence of the series, let's analyze the terms and apply the ratio test. Answer : The limit evaluates to 0, which is less than 1.
The series can be written as:
∑(n=1 to ∞) n^2 * (3/8)^n
Using the ratio test, we compute the limit:
lim(n→∞) |(n+1)^2 * (3/8)^(n+1) / (n^2 * (3/8)^n)|
Simplifying the expression inside the absolute value:
lim(n→∞) |(n+1)^2 * (3/8)^(n+1) / (n^2 * (3/8)^n)|
= lim(n→∞) |(n+1)^2 * (3/8) / (n^2 * (3/8))|
Canceling out common terms:
lim(n→∞) |(n+1)^2 / n^2|
Expanding the numerator:
lim(n→∞) |(n^2 + 2n + 1) / n^2|
Taking the limit as n approaches infinity:
lim(n→∞) |1 + 2/n + 1/n^2|
As n approaches infinity, both (2/n) and (1/n^2) tend to zero, leaving us with:
lim(n→∞) |1|
Since the limit evaluates to 1, the ratio test does not provide a definitive answer. In such cases, we need to consider other convergence tests.
Let's try using the root test instead. The root test states that if the limit of the nth root of the absolute value of the terms is less than 1, the series converges.
We compute the limit:
lim(n→∞) [(n^2 * (3/8)^n)^(1/n)]
Simplifying inside the limit:
lim(n→∞) [(n^(2/n) * ((3/8)^n)^(1/n))]
Taking the nth root of the terms:
lim(n→∞) [n^(2/n) * (3/8)^(1/n)]
Since (3/8) is a constant, we can pull it out of the limit:
(3/8) * lim(n→∞) [n^(2/n) / n]
Simplifying further:
(3/8) * lim(n→∞) [(n^(1/n))^2 / n]
Taking the limit as n approaches infinity:
(3/8) * (1^2 / ∞) = 0
The limit evaluates to 0, which is less than 1. Therefore, by the root test, the series converges.
In summary, both the ratio test and the root test confirm that the series converges.
Learn more about converges : brainly.com/question/29258536
#SPJ11
The total number of hours measured in the units of 100 hours that a family runs a vaccum cleaner over a period of one year in a continuous random variable X that has the density function shown below. Find the probabilfy that over a period of one year, a tamdy runs their vacuum cleaner (a) less than 120 hours; (b) botween 75 and 100 hours f(x)=
⎩
⎨
⎧
x
1
2−x,
0,
0
15x<2
elseratiere
(a) The probabily the fanly fins the vacuum cleaner less than 120 hour is (Type an inieger or deomal rounded to truee decinal places as needed)
Answers
To find the probability that a family runs their vacuum cleaner less than 120 hours over a period of one year, we need to calculate the integral of the density function from 0 to 120.
The probability can be calculated as follows:
P(X < 120) = ∫[0 to 120] f(x) dx
Given the density function:
f(x) = x/2 - x^2/15 for 0 ≤ x ≤ 2
f(x) = 0 for x > 2
Integrating the density function over the range [0, 120]:
P(X < 120) = ∫[0 to 120] (x/2 - x^2/15) dx
To evaluate the integral, we split it into two parts:
P(X < 120) = ∫[0 to 2] (x/2 - x^2/15) dx + ∫[2 to 120] 0 dx
Simplifying the first integral:
P(X < 120) = ∫[0 to 2] (x/2 - x^2/15) dx
= [x^2/4 - x^3/45] evaluated from 0 to 2
= (2^2/4 - 2^3/45) - (0/4 - 0/45)
= (4/4 - 8/45) - 0
= 1 - 8/45
= 37/45 ≈ 0.8222
Therefore, the probability that a family runs their vacuum cleaner less than 120 hours over a period of one year is approximately 0.8222.
The given density function f(x) describes the probability distribution of the random variable X, which represents the total number of hours a family runs their vacuum cleaner in units of 100 hours over a year. The density function is defined differently for different ranges of x.
To find the probability that the family runs the vacuum cleaner less than 120 hours, we need to calculate the cumulative probability up to 120 hours, which is equivalent to integrating the density function from 0 to 120.
By splitting the integral into two parts at x = 2, we can evaluate the integral for the defined range [0, 2] where the density function is non-zero. Integrating the function yields the value (4/4 - 8/45), which simplifies to 37/45.
This means that there is approximately a 0.8222 probability that the family runs their vacuum cleaner for less than 120 hours over the course of one year.
Learn more about integral of the density function here:
brainly.com/question/31772832
#SPJ11
need help math please
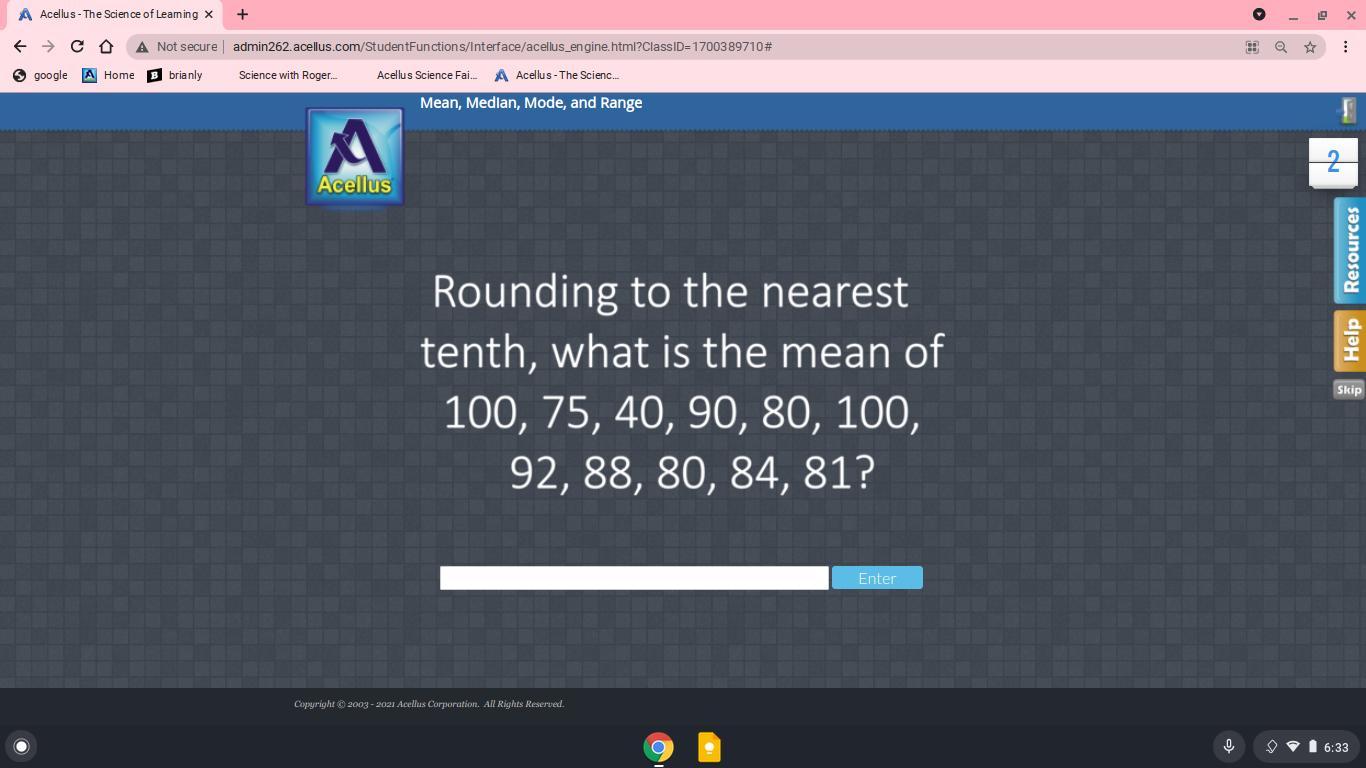
Answers
Answer:
80
Step-by-step explanation:
Rounding to the nearest tenth, we get:
100, 80, 40, 90, 80, 100, 90, 90, 80, 80, 80
Number no. of times
100 2 80 5 40 1 90 380 occurs 5 times (most of the times) so, 80 will be the mean.
HOPE THIS HELPS YOU
Follw me = 10 thanks
Mark as brainliest = 10 thanks
1 thanks to me = 2 thanks
Which sequence of transformations will map figure Konto figure Kí?109876432Х10-9-8--5-4-3-2-11 +2 3 4 5 6 7 8 9 1010Reflection across X = 4, 180° rotation about the origin, and a translation of (x + 8, y)Reflection across X = 4, 180° rotation about the origin, and a translation of (x - 8, y)Reflection across y = 4, 180° rotation about the origin, and a translation of (x + 8, y)Reflection across y = 4, 180° rotation about the origin, and a translation of (x - 8, y)

Answers
Answer:
A
Explanation:
To determine which sequence of transformation will map figure K onto figure K', we test each of the options using the point (6,5) in Figure K.
Option A
Reflection across x=4, 180° rotation about the origin, and a translation of (x+8,y)
\(\left(6,5\right)\rightarrow(2,5)\rightarrow\left(-2,-5\right)\rightarrow(6,-5)\)Option B
Reflection across x=4, 180° rotation about the origin, and a translation of (x-8, y)
\(\left(6,5\right)\rightarrow(2,5)\rightarrow\left(-2,-5\right)\rightarrow(-10,-5)\)Option C
Reflection across y=4, 180° rotation about the origin, and a translation of (x+8,y)
\(\left(6,5\right)\rightarrow(6,3)\rightarrow\left(-6,-3\right)\rightarrow(2,-3)\)Option D
Reflection across y=4, 180° rotation about the origin, and a translation of (x-8,y)
\(\left(6,5\right)\rightarrow(6,3)\rightarrow\left(-6,-3\right)\rightarrow(-14,-3)\)We can see that Option A is the one which maps point (6,5) to (6,-5).
Therefore, it is the sequence of transformations will map figure K onto figure K'.
Marian Plunket owns her own business and is considering an investment. if she undertakes the investment, it will pay $28,000 at the end of each of the new 3 years. the opportunity requires an initial investment of $7,000 plus an additional investment at the end of the second year of $35,000. what is the NPV of this opportunity if the interest rate is 8% per year? Should Marian take it?
Answers
The NPV is positive, it is worth taking the Investment.
Net Present Value (NPV) is an assessment method that determines the attractiveness of an investment. It is a technique that determines whether an investment has a positive or negative present value.
This method involves determining the future cash inflows and outflows and adjusting them to their present value. This helps determine the profitability of the investment, taking into account the time value of money and inflation.The formula for calculating NPV is:
NPV = Σ [CFt / (1 + r)t] – CIWhere CFt = the expected cash flow in period t, r = the discount rate, and CI = the initial investment.
The given problem can be solved by using the following steps:
Calculate the present value (PV) of the expected cash inflows:
Year 1: $28,000 / (1 + 0.08)¹ = $25,925.93Year 2: $28,000 / (1 + 0.08)² = $24,009.11Year 3: $28,000 / (1 + 0.08)³ = $22,173.78Total PV = $72,108.82
Calculate the PV of the initial investment: CI = $7,000 / (1 + 0.08)¹ + $35,000 / (1 + 0.08)²CI = $37,287.43Calculate the NPV by subtracting the initial investment from the total PV: NPV = $72,108.82 – $37,287.43 = $34,821.39
Since the NPV is positive, it is worth taking the investment.
For more questions on Investment.
https://brainly.com/question/29227456
#SPJ8
f + 8 = b5q could you guys help me i don't understand at all
Answers
Answer:
Step-by-step explanation:
are there values for f or b or q? What are we trying to solve?
Given the equation 5z^√6 = 3+i, it is true that (2/5) ^1/6 ei 13/36 π is one of its solutions the equation has a real solution its solutions are the vertices of a square ei π/36 is one of its solutions ( 1/5) ^1/6(cos π/12+isin π/12) is one of its solutions
Answers
Let's evaluate each statement one by one:
1. (2/5)^(1/6) * e^(i(13/36)π) is one of its solutions.
To check if this expression is a solution to the equation, we substitute it into the equation:
5z^(√6) = 3 + i
Using the given expression, we have:
5 * (2/5)^(1/6) * e^(i(13/36)π)^(√6) = 3 + i
Simplifying the expression on the left side:
2^(1/6) * e^(i(13/36)π * (√6)) = 3 + i
This expression does not simplify to match the right side of the equation (3 + i), so it is not a solution.
2. The equation has a real solution.
To determine if the equation has a real solution, we need to find a value for z that satisfies the equation:
5z^(√6) = 3 + i
Since the right side of the equation (3 + i) has an imaginary part, there is no real number z that can satisfy the equation. Therefore, the equation does not have a real solution.
3. Its solutions are the vertices of a square.
The equation 5z^(√6) = 3 + i does not explicitly mention any relationship between its solutions and the vertices of a square. So, this statement is not true.
4. e^(iπ/36) is one of its solutions.
To check if this expression is a solution, we substitute it into the equation:
5z^(√6) = 3 + i
Using the given expression, we have:
5 * e^(iπ/36)^(√6) = 3 + i
Simplifying the expression on the left side:
e^(iπ/36 * (√6)) = (3 + i) / 5
This expression does not simplify to match the right side of the equation (3 + i) / 5, so it is not a solution.
5. (1/5)^(1/6) * (cos(π/12) + i*sin(π/12)) is one of its solutions.
To check if this expression is a solution, we substitute it into the equation:
5z^(√6) = 3 + i
Using the given expression, we have:
5 * ((1/5)^(1/6) * (cos(π/12) + i*sin(π/12)))^(√6) = 3 + i
Simplifying the expression on the left side:
(cos(π/12) + i*sin(π/12))^(√6) = (3 + i) / 5
This expression does not simplify to match the right side of the equation (3 + i) / 5, so it is not a solution.
In conclusion, none of the given expressions (except for the statement about the real solution) are solutions to the equation 5z^(√6) = 3 + i.
Learn more about real solution here:
https://brainly.com/question/32669040
#SPJ11
6. How many ways are there to distribute three different teddy bears and nine identical lollipops to four children: a) Without restriction
Answers
There to distribute three different teddy bears and nine identical lollipops to four children is a) 14080,
Since we have given that Number of teddy bears = 3
Number of identical lollipops = 9
Therefore, the Total number of things
= 3+9
=12
Number of children = 4
(a) Without restriction?
A number of ways would be 4³ x 12c3
= 14080
Therefore, a) 14080,
Learn more about rule of product combinations here:
https://brainly.com/question/2763785
#SPJ4
(a) for what values of x is [infinity] xn n! n = 0 convergent?
Answers
The series [infinity] xn n! n = 0 converges for all real values of x.
The given series [infinity] xn n! n = 0 is a power series with terms xn n! n. To determine the values of x for which the series converges, we can use the ratio test.
The ratio test states that if the limit of the absolute value of the ratio of consecutive terms is less than 1, then the series converges. Let's apply the ratio test to the given series:
lim┬(n→∞)〖|(x(n+1)(n+1)!)/(xn n!)|〗
Simplifying the expression:
lim┬(n→∞)〖|(x(n+1))/(xn)| * 1/(n+1)|〗
As n approaches infinity, the ratio x(n+1)/xn approaches x/x = 1. Additionally, the term 1/(n+1) approaches 0. Therefore, the limit simplifies to:
lim┬(n→∞)〖|1 * 0| = 0|〗
Since the limit is less than 1, the ratio test confirms that the given series converges for all real values of x.
For more questions like Series click the link below:
https://brainly.com/question/28167344
#SPJ11
Match each percent expression to its simplified form.
15% of 75
11.25
7% of 980
27.9
45% of 62
43.56
22 of 198
68.6
Answers
Answer:
Step-by-step explanation:
1) 15% of 75 = (15/100) * 75 = 0.15*75 = 11.25
2) 7% of 980 = 0.07 * 980 = 68.6
3) 45%of 62 = 0.45 * 62 = 27.9
4) 22% of 198 = 0.22 * 198 = 43.56
The model below can be used to find the quotient of one over two divided by one over eight. What is the quotient?
Answers
Answer:
4
Step-by-step explanation:
1/2 goes into 1/8 4 times.
Please help, it'll be appreciated and if possible, I'll give brainliest
ABCD is a parallelogram with diagonals AC and BD intersecting at O
Prove that the diagonals bisect one another

Answers
Step-by-step explanation:
See the attached image. I numbered angles differently so as not to make an assumption that angles numbered the same are congruent.
\(\overline{AB} \parallel \overline{CD}\\\angle1 \cong \angle3\) (alternate interior angles are congruent)
\(\overline{AD} \parallel \overline{BC}\\\angle 2 \cong \angle 4\) (alternate interior angles are congruent)
\(\overline{AB} \cong \overline{CD}\) (opposite sides of a parallelogram are congruent)
\(\triangle{ABO \cong \triangle{CDO}\) (ASA - side/angle/side)
\(\overline{AO} \cong \overline{CO}\\\overline{BO} \cong \overline{DO}\) (corresponding parts of congruent triangles are congruent)
The diagonals bisect each other!

which term describes the percent of voters casting ballots?
Answers
The term which is used for describing the number of voters who casted their votes using the ballots is called as voter turnout.
The process of selecting a candidate for a suitable post who takes care of the policies which will be framed for the people is called as voting. In this process, the members/ citizens casts their vote in the favor of their suitable candidate. Many times voters are not valid and their votes are considered as null and void.
The voter turnout is either the percentage of registered voters, eligible voters, or all voting-age people ( this varies from place to place depending upon the minimum voting age required). The voter turnout is also referred to the number of people who go to it or take part in it. High voter turnout is generally considered a sign of a healthy democracy.
Learn more about voter turnout at:
brainly.com/question/29639449
#SPJ4
Please help me I need to get my grade up!

Answers
The measure of ∠XYZ is 130°. Option C is the correct option.
What is an isosceles triangle?
An isosceles triangle in geometry is a triangle with two equal-length sides. Sometimes it is stated to have exactly two sides that are the same length, and other times it is stated to have at least two sides that are the same length, with the latter version including the equilateral triangle as an exception.
Given that the length of YZ = YX and ∠YZX = 25°.
There is an agreement between two sides. The base of an isosceles triangle refers to the third side of the triangle, which is unequal to the other two sides. The two angles that are opposite the equal sides line up perfectly.
According to the property of the isosceles triangle:
∠YXZ = ∠YZX = 25°
The sum of all angles of a triangle is 180°.
Therefore,
∠YXZ + ∠YZX + ∠XYZ = 180°
25° + 25° + ∠XYZ = 180°
50° + ∠XYZ = 180°
∠XYZ = 180° - 50°
∠XYZ = 130°
To learn more about isosceles triangle, click on the below link:
https://brainly.com/question/29618319
#SPJ1
Makayla leans a 18-foot ladder against a wall so that it forms an angle of 64 degrees with the ground. What’s the horizontal distance between the base of the ladder and the wall?
Answers
The horizontal distance between the base of the ladder and the wall is approximately 16.06 feet.
To find the flat distance between the foundation of the stool and the wall, we utilize geometry. For this situation, we can utilize the sine capability, which relates the contrary side of a right triangle to the hypotenuse and the point inverse the contrary side.
Let x be the flat distance between the foundation of the stepping stool and the wall. Then, utilizing the given point of 64 degrees, we can compose:
sin(64) = inverse/hypotenuse
where the hypotenuse is the length of the stepping stool, which is 18 feet.
Addressing for the contrary side, which is the even distance we need to find, we get:
inverse = sin(64) x hypotenuse
inverse = sin(64) x 18
inverse = 16.06 feet
Accordingly, the even distance between the foundation of the stepping stool and the wall is roughly 16.06 feet.
To learn more about Trigonometry, refer:
https://brainly.com/question/30350752
#SPJ4
What is the image point of ( − 7 , 0 ) (−7,0) after a translation left 4 units and up 1 unit?
Answers
Answer: (-12,1)
Step-by-step explanation:
1. The point (-7,0) is first translated to the left 4 units. This will result in (-12,0).
2. The point is then translated one unit up, resulting in (-12,1).
