Different fuels produce different amounts of heat energy when burned. For example propane has a heat energy of 2,470 btu/ft^3 how much energy can propane tank with a volume of 43. 7 ft^3 produce
Answers
A propane tank with a volume of 43.7 ft³ can produce 107,639 BTUs of heat energy when burned.
Propane is a commonly used fuel for heating and cooking. It has a heat energy content of 2,470 BTUs per cubic foot (ft³). To calculate how much energy a propane tank with a volume of 43.7 ft³ can produce, we need to use a simple formula:
Energy = Volume x Energy Content
Plugging in the values we have:
Energy = 43.7 ft³ x 2,470 BTU/ft³
Energy = 107,639 BTUs
To know more about volume here
https://brainly.com/question/11168779
#SPJ4
Related Questions
Trent train is traveling at the speed of 10m/s at the top of a hill. Five seconds later it reaches the bottom of the hill and is moving at 39 m/s. What is the rate of acceleration of Trent train?
Answers
Answer:
5.8ms^2
Step-by-step explanation:
The rate of acceleration of Trent train is 5.8 m/s².
What is acceleration?The rate at which velocity changes is called acceleration. Acceleration typically indicates a change in speed, but not necessarily. An item that follows a circular course while maintaining a constant speed is still moving forward because the direction of its motion is shifting.
Given:
Initial velocity, u = 10 m/s
Final Velocity, v = 39 m/s
Time = 4 seconds
So, Acceleration = (v - u) / t
a = ( 39- 10)/5
a = 29/5
a = 5.8 m/s²
Hence, the acceleration is 5.8 m/s².
Learn more about acceleration here:
https://brainly.com/question/12550364
#SPJ2
write the absolute value equation that has the following solution(s). Two solutions: x=2, x=14.
Answers
Answer:
\(|x-8|=6\)
Step-by-step explanation:
Let's begin by finding the midpoint of 2 and 14. To do this, we'll add the numbers and then divide by 2.
2+14=16
16/2=8
The number that is the same distance between 2 and 14 is 8.
Now, let's find how far away each number is from 8.
8-2=6
14-8=6
2 and 14 are 6 away from 8.
Let's set up the absolute value equation using these two values.
Since 8 is the midpoint, this will be what the absolute value expression is equal to.
Since each number is 6 away from 8, this is the number (6) we will be taking away from 2 and 14.
Remember that absolute value is just distance.
In other words, 2 is 6 away from 8, and 14 is also 6 away from 8.
Or, the distance between a number x and 8 is 6.
Using this knowledge, we have:
\(|x-8|=6\)
Answer:
|x-8|=6
Step-by-step explanation:
i checked rsm its correct :3
1 15/100 + 1/50 + 1.175
Answers
Answer:
Step-by-step explanation:
Change fractions to have the same denominator or change them all to a decimal. Then add.
Decimal method:
1 and 15/100 is equal to 1.15
1/50 is equal to 0.02
The final term is already a decimal
Add. 1.15 + 0.02 + 1.175 = 2.345
Part a. **22.8
write a program that finds all prime numbers up to 10,000,000. there are approximately 5,761,455 such prime numbers. your program should meet the following requirements:
Part b. Implement a method that open file PrimeNumbers.dat and perform the following
Answers
We have that, to develop a program that finds prime numbers and one that will be a file, it is necessary to use pseudocode, using cycles and files with lists
How do we develop the programs?a. To write a program that finds all prime numbers up to 10,000,000, the following steps can be followed:
1. Set up a loop to iterate through all the numbers from 2 to 10,000,000.
2. Check if the number is prime by dividing it by all the previous numbers.
3. If the number is not divisible by any previous number, it is a prime number.
4. Add the prime number to a list of prime numbers.
5. Repeat the cycle until all prime numbers up to 10,000,000 have been found.
b. To implement a method that opens the PrimeNumbers.dat file and does the following, the following steps can be followed:
1. Create a method that opens the PrimeNumbers.dat file.
2. Use a loop to go through all the lines of the file.
3. For each line, parse the content into a string.
4. Check if the string is a prime number divided by all previous numbers.
5. If the number is not divisible by any previous number, it is a prime number.
6. Add the prime number to a list of prime numbers.
7. Repeat the loop until all the prime numbers in the file have been found.
8. Returns the list of prime numbers.
See more information about pseudocode at: https://brainly.com/question/24953880
#SPJ11
3. 6x + 7y =7 4. 2x - y = -3
Answers
For the first graph
A = (-5, 2)
B = (5, -4)
To calculate the slope we will use the following formula
\(\begin{gathered} m=\frac{-4-2}{5-(-5)} \\ m=\frac{-6}{10} \\ m=\frac{-3}{5} \end{gathered}\)The answer would be m = -3/5
For the second graph
A = (-1, -1)
B = (3, 0)
To calculate the slope we will use the following formula
\(\begin{gathered} m=\frac{0-(-1)}{3-(-1)} \\ m=\frac{1}{4} \\ \end{gathered}\)The answer would be m = 1/4
For the third graph
In the third graph, we have a vertical slope at point x = 2
In this case the slope would be equal to infinity and the equation of the line would be equal to x = 2
\(m=\infty\)
HELP PLEASE. I DONT KNOW IF ITS 30 OR 180

Answers
To see why, we can simplify √180 as follows:
√180 = √(36 × 5) (since 36 is a perfect square that can be factored out)
√180 = √36 × √5 (using the product rule of square roots)
√180 = 6√5
Therefore, 6√5 is equivalent to √180.
Answer:
Step-by-step explanation:
6\(\sqrt{5\\\)
\(\sqrt{5*36}\)
\(\sqrt{180}\)
If you think about it logically, how can you take 6 out? So there was a number 36 under the root, and because of that there is a possibility to take it out, because 6 squared is 36
The area of a circular Garden is 3850cm^2. Find the length of wire of sturns.
Answers
Answer is 35cm hope it will help you .

EXPLAINATION: π.r² = 3850 cm²
⇒ r² = 3850/π = 3850/3,14 ≈ 1225.5
⇒ r = √ 1225.5 ≈ 35 cm
P/s: π ≈ 3.14
ANSWER: r = 35 cm
Ok done. Thank to me :>
100% =3200
70% = ????
Answers
Answer:
2240
Step-by-step explanation:
plz fo"ow ms
mark me as brainlist
to find out percentages in the future, on your calculator and type 3200 and then minus 70% and that’s your answer! :)
1/5 x 1/5 x 1/5 x 1/5
Answers
-1/2 x -3/5 this is what i need help with.
Answers
Answer:
3/10 or 0.3
Step-by-step explanation:
Help me please !!!!!!

Answers
Answer:
wouldnt it be. 4 × x+7
Step-by-step explanation:
because x and 7 equal the whole top and 4 is the side
Find area of the shaded region.
Area of addition and subtraction, trigonometry, and sohcahtoa.
I’ve wasted many pints asking, please I ask kindly that no one puts fake answers, I truly need help with these problems and it is inconsiderate of those who post an answer for points so please respect others.

Answers
Answer:
The area of the shaded region is about 38.1 square centimeters.
Step-by-step explanation:
We want to find the area of the shaded region.
To do so, we can first find the area of the sector and then subtract the area of the triangle from the sector.
The given circle has a radius of 6 cm.
And the given sector has a central angle of 150°.
The area for a sector is given by the formula:
\(\displaystyle A=\pi r^2\cdot \frac{\theta}{360^\circ}\)
In this case, r = 6 and θ = 150°. Hence, the area of the sector is:
\(\displaystyle \begin{aligned}A&=\pi(6)^2\cdot \frac{150}{360}\\ &=36\pi\cdot \frac{5}{12}\\&=3\pi \cdot 5\\&=15\pi \text{ cm}^2\end{aligned}\)
Now, we can find the area of the triangle. We can use an alternative formula:
\(\displaystyle A=\frac{1}{2}ab\sin(C)\)
Where a and b are the side lengths, and C is the angle between them.
Both side lengths of the triangle are the radii of the circle. So, both side lengths are 6.
And the angle C is 150°. Hence, the area of the triangle is:
\(\displaystyle A=\frac{1}{2}(6)(6)\sin(150)=18\sin(150)\)
The area of the shaded region is equivalent to the sector minus the triangle:
\(A_{\text{shaded}}=A_{\text{sector}}-A_{\text{triangle}}\)
Therefore:
\(A_{\text{shaded}}=15\pi -18\sin(150)\)
Use a calculator:
\(A_{\text{shaded}}=38.1238...\approx 38.1\text{ cm}^2\)
The area of the shaded region is about 38.1 square centimeters.
May I ask why the correct answer is A?

Answers
Answer: A
Step-by-step explanation:
For II, when the numerator is expanded, it contains terms of ab and a^2 which makes it a quadratic function, not an algebraic function.
For III, tricky one. The a can be cancelled out in the numerator and denominator and the resulting fraction is (b-3)/3. However, this can be further simplified to 1/3b - 1, which makes it not an algebraic fraction anymore.
9.
Find the area of the triangle.
6ft
9ft
Area =
ft?
Enter the answer
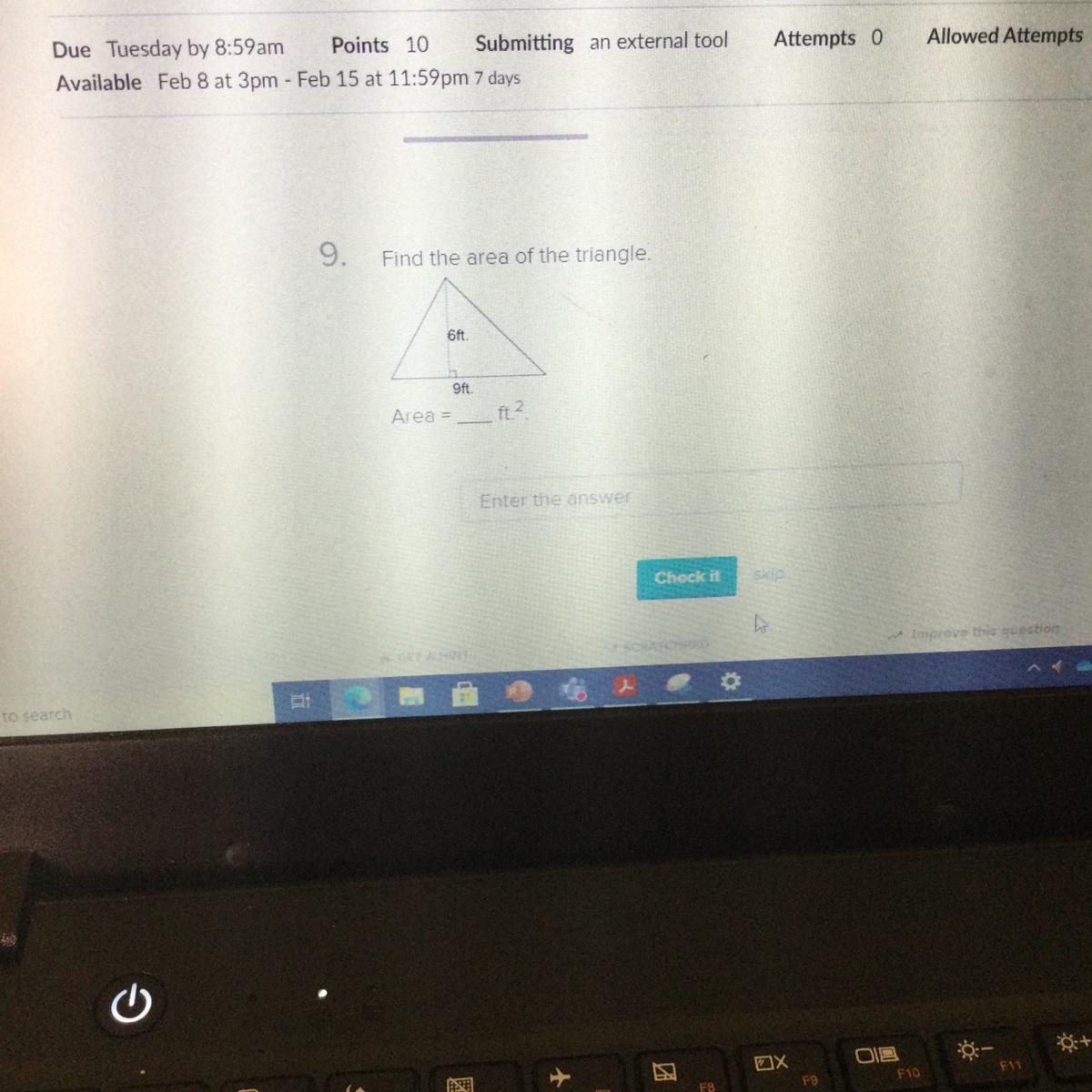
Answers
Answer:
Area= 24ft squared
Step-by-step explanation:
Area= 1/2 Bh
A= 1/2 9(6)
A= 1/2 48
A= 24ft
I NEED HELP W THIS QUICK FIRST TO ANSWER CAN HAVE BRAINLIEST I GUESS
i added more pts cus idrc for em



Answers
Answer:
1. Multiply the slope by 2 and look at the numerator
2. 5/7
3. slide A
4. The run of slide a is shorter which means that its steeper because the rise is the same
5. 10
6. 5 units?
Step-by-step explanation:
#1
We would use the slopeWe know
slope=tanØ
Here in slide B
tanØ=5/9But
tanØ=Ladder/18Then
9Ladder=90Ladder=90/9=10ft#2
The slope of slide A
tanØ=15/21tanØ=5/7#3 and 4
Compare tangents
tan(5/7)>tan(5/9) as their difference is +veSlide A is steeper
#5
Found in #1
#6
Slide A is higher as 15>10
Find the exact value of cos0. Express your answer as a fraction.

Answers
Trigonometric Functions -
\( \cos = \frac{adjacent}{hypotenuse} \)
Find the opposite side, first of all.
Pythagorean Theorem -
\(a^{2} + b^{2} = c^{2} \)
Input the hypotenuse and opposite sides to find b^2.
\(49 + {b}^{2} = 64\)
Minus 49 from equations to get b^2 by itself.
\( {b}^{2} = 15\)
Square root b^2 and 15 to get b by itself.
\(b = \sqrt{15} \)
Now we can get to the trigonometry functioms!
\( \frac{ \sqrt{15} }{8} \)
Divide them up, then find the percentage!
48% or...
\( \frac{ \sqrt{15} }{8} \)
Find the area under the standard normal distribution curve between z=0 and z=0. 98
Answers
The area under the standard normal distribution curve between z = 0 and z = 0.98 is:
0.8365 - 0.5000 = 0.3365
To find the area under the standard normal distribution curve between z = 0 and z = 0.98, we can use a standard normal distribution table or a calculator that can compute normal probabilities.
Using a standard normal distribution table, we can look up the area corresponding to a z-score of 0 and a z-score of 0.98 separately and then subtract the two areas to find the area between them.
The area under the standard normal distribution curve to the left of z = 0 is 0.5000 (by definition). The area under the curve to the left of z = 0.98 is 0.8365 (from the standard normal distribution table).
So the area under the standard normal distribution curve between z=0 and z=0.98 is approximately 0.3365.
To know more about area under curve refer here
https://brainly.com/question/40445978#
#SPJ11
It is known that the birth weights of full-term newborn infants in the U.S. have an approximately normal distribution with a mean weight of 6.8 lbs and a standard deviation of 1.7 lbs. How much would a baby need to weigh at birth (in lbs) to be considered in the 90th percentile of birth weights
Answers
To be in the 90th percentile of birth weights, a baby would need to weigh approximately 8.976 lbs at birth.
The 90th percentile corresponds to the value below which 90% of the data falls.
In this case, we have a normal distribution with a known mean and standard deviation of birth weights. To find the weight at the 90th percentile, we can use the properties of the standard normal distribution.
First, we convert the percentile to a Z-score using a Z-table or calculator. For the 90th percentile, the Z-score is approximately 1.28.
Next, we can use the Z-score formula to calculate the corresponding weight:
Z = (x - mean) / standard deviation
By rearranging the formula and substituting the values:
1.28 = (x - 6.8) / 1.7
Solving for x, the weight at the 90th percentile, we have:
1.28 * 1.7 = x - 6.8
2.176 = x - 6.8
x = 2.176 + 6.8
x ≈ 8.976 lbs
Therefore, a baby would need to weigh approximately 8.976 lbs at birth to be considered in the 90th percentile of birth weights.
Learn more about Standard deviation click here brainly.com/question/13708253
#SPJ11
Determine the quadratic function of the form f(x)= a(x - h)² + k whose graph is given on the
right.

Answers
The quadratic function will be f(x) = 2\(x^{2}\) + 4x + 15
General equation of quadratic is
f(x) = a\(x^{2}\) + bx + c
and Standard form is
f(x) =a \((x-h)^{2}\) + k
where h , k are coordinates of vertex
and x , y represent some point on the graph.
By replacing f(x) with y in standard equation we get
y = a\((x-h)^{2}\) + k
Put value of x , y , h , k from the graph.
h = -2
k = 7
x = 0
y = 9
9 = a (4) + 7
a = 2
Now put value of a in standard equation
f(x) = 2 \((x + 2)^{2}\) + 7
f(x) = 2\(x^{2}\) + 4x + 15
To know more about quadratic equation
https://brainly.com/question/27953127
#SPJ1
I really need help on 16 and 18 I'm super confused problem because I'm tired but I really need help

Answers
Answer:
Hello,
Step-by-step explanation:
16)
Area of the square= 5²=25 (unit of square)
17)
Volume of the cube =3^3 =27 (unit of volume)
18)
side of the cube =5 (unit of lenght)
Volume of the cube = (5 (unit of lenght)) ^3
=125 * (unit of lenght)^3 =125 (unit of volume)
Solve for y.
x + a=yb
O y=x+a-b
O y= (x+a)
b
O y= (x+a)
b

Answers
Answer:
The answer is the 2nd bullet point (B)
Factor –7x3 21x2 3x – 9 by grouping. what is the resulting expression?
Answers
The resulting expression on factorization by grouping method is (3-7x²)(x-3).
What is Factorization?Factorization is a method in which an Integer or an expression is written in terms of product of its fractions.
The expression given in the question is
–7x³ + 21x² + 3x – 9
This equation has to be factorized using grouping method.
group of two or more is formed and common term is taken out.
-7x² (x -3) +3(x-3)
( -7x²+3) (x-3)
(3-7x²)(x-3)
The resulting expression on factorization by grouping method is
(3-7x²)(x-3).
To know more about Factorization
https://brainly.com/question/24182713
#SPJ1
Which formula is not equivalent to the other two? (-1k-3 k +3 k+ 4 ks4 Choose the correct answer below. k+3 ke-2 k-3 ks4 (-が k +4 k -3
Answers
The correct answer is k+3 ke-2.
To determine which formula is not equivalent to the other two, we can compare each formula step-by-step. Let's analyze each formula:
1. (-1k-3 k +3 k+ 4 ks4
2. k+3 ke-2
3. k-3 ks4
Starting with formula 1, we can see that it consists of three terms: -1k-3, k+3, and k+4ks4. Each term is separated by a space.
Moving on to formula 2, we have k+3ke-2. This formula also consists of three terms: k+3, k, and e-2. In this case, we have a variable (k) combined with two different exponents (3 and -2).
Finally, formula 3 is k-3ks4. It consists of two terms: k-3 and ks4. Again, each term is separated by a space.
Comparing the three formulas, we can see that formula 1 has three terms, while formulas 2 and 3 have two terms each. Additionally, formula 1 includes the term k+4ks4, which is not present in formulas 2 and 3.
Therefore, the formula that is not equivalent to the other two is k+3 ke-2.
To know more about equivalent here:
brainly.com/question/25197597
#SPJ11
under the good samaritan law, you can not be held liable for trying to help someone at a traffic collision if you helped in good faith. state of true or false
a. true
b. false
Answers
Answer: true
Step-by-step explanation:
The good Samaritan law allows you to help people and not be liable for trying to do so.
find the value of given expression
\( \sqrt{300 \times 3} \)
Answers
Answer:
√(300×3)=√900=√30²=±30 is your answer
Aprobability experiment is conducted in which the sample space of the experiment is S-(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12), event F-(2, 3, 4, 5, 6), and event G(6, 7, 8, 9) Assume that each outcome
Answers
The probability of the P(F or G) is 0.667.
A probability experiment is conducted in which the sample space of the experiment is S={ 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}, event F={5, 6, 7, 8, 9}, and event G={9, 10, 11, 12}. Assume that each outcome is equally likely.
To list the outcomes in F or G, we need to combine both events F and G and eliminate any duplicates.
So, the outcomes in F or G are:
F or G = {5, 6, 7, 8, 9, 10, 11, 12}
Hence, A. F or G = { 5, 6, 7, 8, 9, 10, 11, 12}
Next, to find P(F or G) by counting the number of outcomes in F or G, we can use the formula:
P(F or G) = n(F or G) / n(S)
where, n(F or G) is the number of outcomes in F or G and n(S) is the number of outcomes in the sample space.
So, n(F or G) = 8 and n(S) = 12
Hence, P(F or G) = n(F or G) / n(S) = 8/12 = 0.667 (rounded to three decimal places)
Therefore, B. P(F or G) = 0.667
Finally, to determine P(F or G) using the general addition rule, we can use the formula:
P(F or G) = P(F) + P(G) - P(F and G)
where, P(F) and P(G) are the probabilities of events F and G, and P(F and G) is the probability of the intersection of events F and G.
To find P(F and G), we can use the formula:
P(F and G) = n(F and G) / n(S)
where, n(F and G) is the number of outcomes in both F and G.
So, n(F and G) = 1
Hence, P(F and G) = n(F and G) / n(S) = 1/12
Therefore, A. P(F or G) = (5/12) + (4/12) - (1/12) = 8/12 = 0.667 (rounded to three decimal places)
To learn more about probability refer here
https://brainly.com/question/32004014#
#SPJ11
5
Which of the following expressions are equivalent to
ܗ | ܚ
?
3
Choose all answers that apply:
-5
A
-3
B
color
None of the above
Answers
Answer:
a
Step-by-step explanation:
i did this in middle shoool
hehe
I’m a bit stuck right now
Answers
Given:
The speed of driver is 99 miles/hour.
The objective is to find the speed in kilometers/hour and kilometers/minute.
Explanation:
Conversion of miles/hour to kilometers/hour:
Since it is given that 1 mile = 1.61 kilometers.
\(\begin{gathered} 99\text{ miles/hour=99 miles/hour(}\frac{1.61\text{ kilometers}}{1\text{ miles}}\text{)} \\ =159.39\text{ kilometers/hour} \\ \approx159.4\text{ kilometers/hour} \end{gathered}\)Conversion of kilometers/hour to kilometers/minute:
Since, it is given that 1 hour = 60 minutes.
\(\begin{gathered} 99\text{ miles/hour=99miles/hour(}\frac{1.61\text{ kilometers}}{1\text{ miles}})(\frac{1\text{ hour}}{60\text{ minutes}}) \\ =2.6565\text{ kilometers/minute} \\ \approx2.7\text{ kilometers/minute} \end{gathered}\)Hence, speed is equivalent to 159.4 kilometers/hour or 2.7 kilometers/minute.
find the general solution of the given higher-order differential equation. d 4y dx4 − 2 d 2y dx2 − 8y = 0
Answers
he required solution is \(y=c_1e^{2x}+c_2e^{-2x}+c_3\sqrt2\cos(\sqrt2x)+c_4\sqrt2\sin(\sqrt2x)\)
where \(c_1,c_2,c_3\) and \(c_4\) are constants.
Let’s assume the general solution of the given differential equation is,
y=e^{mx}
By taking the derivative of this equation, we get
\(\frac{dy}{dx} = me^{mx}\\\frac{d^2y}{dx^2} = m^2e^{mx}\\\frac{d^3y}{dx^3} = m^3e^{mx}\\\frac{d^4y}{dx^4} = m^4e^{mx}\\\)
Now substitute these values in the given differential equation.
\(\frac{d^4y}{dx^4}-2\frac{d^2y}{dx^2}-8y\\=0m^4e^{mx}-2m^2e^{mx}-8e^{mx}\\=0e^{mx}(m^4-2m^2-8)=0\)
Therefore, \(m^4-2m^2-8=0\)
\((m^2-4)(m^2+2)=0\)
Therefore, the roots are, \(m = ±\sqrt{2} and m=±2\)
By applying the formula for the general solution of a differential equation, we get
General solution is, \(y=c_1e^{2x}+c_2e^{-2x}+c_3\sqrt2\cos(\sqrt2x)+c_4\sqrt2\sin(\sqrt2x)\)
Hence, the required solution is \(y=c_1e^{2x}+c_2e^{-2x}+c_3\sqrt2\cos(\sqrt2x)+c_4\sqrt2\sin(\sqrt2x)\)
where \(c_1,c_2,c_3\) and \(c_4\) are constants.
Know more about constants here:
https://brainly.com/question/27983400
#SPJ11
Prove that tanx sinx + cosx = secx
Answers
The proof that tan(x) sin(x) + cos(x) = sec(x) is represented by the trigonometric equation sec(x) = sec(x)
How to prove the trigonometric equationFrom the question, we have the following parameters that can be used in our computation:
tan(x) sin(x) + cos(x) = sec(x)
Express tan(x) as sin(x)/cos(x)
So, we have the following representation
sin(x)/cos(x) * sin(x) + cos(x) = sec(x)
Evaluate the products
So, we have the following representation
sin²(x)/cos(x) + cos(x) = sec(x)
Take the LCM
[sin²(x) + cos²(x)]/cos(x) = sec(x)
Express sin²(x) + cos²(x) as 1
So, we have
1/cos(x) = sec(x)
Evaluate
sec(x) = sec(x)
Hence, the equation has been proved
Read more about trigonometric equation at
https://brainly.com/question/24349828
#SPJ1