Answers
Therefore the equation of the line in function-form is f(x)=-2x-1
An equation of a line on the cartesian plane is given by y=mx+c. Here m denotes the slope of the line and c denotes the y-intercept.
Slope of a line is defined as the inclination of the line along the positive x- axis . Slope is calculated by the formula \(m=\frac{y_2-y_1}{x_2-x_1}.\) where \((x_1,y_1)\) and \((x_2,y_2)\) are two points on the line.
y-intercept is defined as the point where the line passes through the y-axis.
From the graph we can see that the line passes through (0,-1)and (-1,1)
therefore slope of the line is
\(m=\frac{y_2-y_1}{x_2-x_1}\\or, m=\frac{1-(-1)}{-1-0}\\or, m=-2\)
Now we know that the equation of a line passing through a point \((x_1,y_1)\) and with slope m is given by
\(y-y_1=m(x-x_1)\\\)
Substituting the values in the equation we get
y-(-1)=-2(x-0)
or, y=-1-2x
Therefore the equation of the line in function-form is f(x)=-2x-1 .Hence the second option is correct.
To learn more about the equation of the line visit:
https://brainly.com/question/21511618
#SPJ9
Related Questions
Y=2x-Pq make x the subject
Answers
Which point could not be part of a function that includes (3, -1), (4, 2), (5, 4), (-2, 0), and (8, -3)?
(6, -7)
(2,2)
(3, -2)
(7, 4)
Answers
Answer:
(3, -2) is the correct choice.
In a survey, people were asked whether they like baseball or whether they like hockey. Here are the results: Likes hockey Doesn’t like hockey Likes baseball 12 18 Doesn’t like baseball 14 6 What value is missing to convert the two-way table to a two-way relative frequency table? Likes hockey Doesn’t like hockey Likes baseball 0.24 0.36 Doesn’t like baseball 0.28
Answers
The missing value 'x' in the two-way relative frequency table is 0.36.
To convert the two-way table to a two-way relative frequency table, we need to calculate the relative frequencies for each category. Relative frequency is calculated by dividing the frequency of a particular category by the total count in that row or column.
Let's denote the missing value as 'x'. To find the value of 'x', we need to ensure that the sum of the relative frequencies in each row and each column adds up to 1.
First, let's calculate the relative frequencies for each category:
Likes hockey: The total count in this row is 12 + 18 = 30.
Relative frequency of "Likes hockey" = 12/30 = 0.4
Relative frequency of "Doesn't like hockey" = 18/30 = 0.6
Likes baseball: The total count in this column is 12 + 14 = 26.
Relative frequency of "Likes baseball" = 12/26 ≈ 0.4615
Relative frequency of "Doesn't like baseball" = 14/26 ≈ 0.5385
To ensure that the relative frequencies add up to 1, we can set up the following equations:
0.4 + x = 1 (sum of relative frequencies in the "Likes hockey" row)
0.4615 + 0.5385 + x = 1 (sum of relative frequencies in the "Likes baseball" column)
Simplifying the equations, we have:
x = 0.6 (1 - 0.4) = 0.6 * 0.6 = 0.36
For more such questions on relative frequency
https://brainly.com/question/27562468
#SPJ8
fast help me please and thank you

Answers
Answer:
c
Step-by-step explanation:
-3-- or just + -3 * -1 since xy are not separated by anything so its multiplication
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
Solve the system
0.2x+y=1.3
2(0.5x-y)=4.6
Answers
Answer:
x = 36/7 (or approximately 5.143); y = 19/70 (or approximately 0.271)
Step-by-step explanation:
First, we can distribute the 2 to have both equations look similar:
\(2(0.5x-y)=4.6\\x-2y=4.6\)
Now, we can eliminate the ys by multiplying the entire first equation by 2. This will allow us to solve for x.
\(2(0.2x+y=1.3)\\\\0.4x+2y=2.6\\x-2y=4.6\\\\1.4x=7.2\\x=\frac{36}{7}\\ x=5.142857143\)
Now, we can plug in 36/7 for x in any of the two equations:
\(0.2(\frac{36}{7})+y=1.3\\ \frac{36}{35}+y=1.3\\ y=\frac{19}{70}\\ y=0.2714285714\)
If you use the decimal answers, you can round as much as you need.
A 12 cm by 12 cm square piece of paper has 5 holes punched out of it. 4 of the holes are circles of radius 3 cm and 1 of the holes is a circle of radius 1 cm. The paper and punched holes can be visually interpreted as below. Determine the area of paper remaining after the holes have been punched out.

Answers
5 holes have been punched into a 12 cm by 12 cm square piece of paper. The area of remaining paper will be 27.714 cm².
Firstly, we will calculate the area of the square of paper in which the holes are punched.
Side of square = 12 cm
Area of square = side²
= (12) ²
= 144 cm²
Now, we will calculate the area of the bigger punch holes
Radius of big punch hole = 3 cm
Area of 1 big punch = π (radius) ²
= 22/7 × (3)²
22 / 7 × 9
= 198 / 7 cm²
Area of 4 punches = 4 × 198/7
= 792/7 cm²
Now, we will calculate the area of smaller punch whose radius is 1cm
Area = 22/7 × 1²
= 22/7 cm²
Now, we will calculate the total area covered by circles
Total area covered by circles = area of small punch + area of 4 big punch
= 22/7 + 792/7
= 814 /7 cm²
Remaining area = area of square - area of circles
= 144 - 814/7
= (1008 - 814) / 7
= 194 / 7
= 27.714 cm²
To know more about area:
https://brainly.com/question/27683633
#SPJ1
(−2k + 3kª + 2k³) − (−12k – k³ + 8)
Answers
The simplified expression of (−2k + 3kª + 2k³) − (−12k – k³ + 8) is 10k + 3kª + 3k³ - 8.
Let's simplify the expression step by step:
(−2k + 3kª + 2k³) − (−12k – k³ + 8)
First, let's distribute the negative sign to the terms inside the second parentheses:
−2k + 3kª + 2k³ + 12k + k³ - 8
Next, let's combine like terms:
(-2k + 12k) + (3kª + k³) + (2k³ - 8)
Simplifying further:
10k + 3kª + k³ + 2k³ - 8
Combining the terms with k³:
10k + 3kª + 3k³ - 8
So, the simplified expression is 10k + 3kª + 3k³ - 8.
For more such questions on expression , Visit:
https://brainly.com/question/1859113
#SPJ11
Expand the function.
f(x) = (3x-4)4
81x4 − 432x³ + [? ]x²
+
-
X +
PLS HELP
Answers
The expansion of the function \((3x - 4)^4\) simplifies to \(81x^4 - 432x^3 + 864x^2 - 768x + 256.\)
To expand the function \(f(x) = (3x - 4)^4\), we can use the binomial theorem. According to the binomial theorem, for any real numbers a and b and a positive integer n, the expansion of \((a + b)^n\) can be written as:
\((a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^{(n-1)} b^1 + C(n, 2)a^{(n-2)} b^2 + ... + C(n, n-1)a^1 b^{(n-1)} + C(n, n)a^0 b^n\)
where C(n, k) represents the binomial coefficient, which is given by C(n, k) = n! / (k!(n-k)!).
Applying this formula to our function \(f(x) = (3x - 4)^4\), we have:
\(f(x) = C(4, 0)(3x)^4 (-4)^0 + C(4, 1)(3x)^3 (-4)^1 + C(4, 2)(3x)^2 (-4)^2 + C(4, 3)(3x)^1 (-4)^3 + C(4, 4)(3x)^0 (-4)^4\)
Simplifying each term, we get:
\(f(x) = 81x^4 + (-432x^3) + 864x^2 + (-768x) + 256\)
Therefore, the expanded form of the function \(f(x) = (3x - 4)^4\) is \(81x^4 - 432x^3 + 864x^2 - 768x + 256\).
Note that the coefficient of \(x^3\) is -432, the coefficient of \(x^2\) is 864, the coefficient of x is -768, and the constant term is 256.
For more question on function visit:
https://brainly.com/question/11624077
#SPJ8
Note the complete question is
![Expand the function.f(x) = (3x-4)481x4 432x + [? ]x+-X + PLS HELP](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/GfWbZg9TGTD1FI7gZnK9lbVdLBpjkw5X.jpeg)
What is the slope of (4, -3) and (4, 2)
Answers
Answer:
Slope is undefined.
Step-by-step explanation:
-3-2
——
4-4
Anything with the x value as zero is undefined.
Answer:
unidentified slope of 0
Step-by-step explanation:
Use the slope formula: \(\frac{y2-y1}{x2-x1}\)
2 is y2, -3 is y1, 4 is x2, and 4 is x1.
\(\frac{2-(-3)}{4-4}\)
\(\frac{2+3}{0}\)
\(\frac{5}{0} =0\)
The slope is 0. That means the slope is unidentified. I hope this helps!
Review the information given based on a principal balance of $18,000 to answer the question:
FICO Score Simple Interest Rate Total # of Payments Total Amount Paid
800-850 12%
29
740-799 15%
33
670-739 18%
38
48
580-669 21%
300-579 28%
60
$20,160.00
$20,700.00
$21,240.00
$21,780.00
$23,040.00
Calculate the percent increase in the amount of interest paid between a household with a 740 credit score and one with a
730 credit score. Round the final answer to the nearest tenth. (4 points)
O 20.0%
O 17.3%
O 19.5%
O 18.4%

Answers
Answer:
To calculate the percent increase in the amount of interest paid between a household with a 740 credit score and one with a 730 credit score , we need to find the total amount paid for each score and then calculate the percent increase.
From the given table , we can see that the simple interest rate for a credit score of 740-799 is 15%, and the total number of payments is 33 . So, the total amount paid for a principal balance of $18,000 with a credit score of 740 is:
Principal + Total Interest = Total Amount Paid
$18,000 + ($18,000 * 15% * 33/12) = $20,700
Similarly, for a credit score of 730, we need to use the simple interest rate for a credit score of 670-739 , which is 18%, and the total number of payments is 38. So, the total amount paid for a principal balance of $18,000 with a credit score of 730 is:
Principal + Total Interest = Total Amount Paid
$18,000 + ($18,000 * 18% * 38/12) = $21,240
Now, to calculate the percent increase in the amount of interest paid , we can use the following formula:
Percent increase = |(New value - Old value) / Old value| * 100%
Plugging in the values, we get:
Percent increase = |($21,240 - $20,700) / $20,700| * 100%
Percent increase = 2.6%
Rounding to the nearest tenth, we get the final answer as:
Percent increase = 2.6% ≈ 2.5% (rounded to the nearest tenth)
Therefore, the answer is O 2.5%.
Step-by-step explanation:
y = 2x - 9
Determine the slope and the y-intercept (entered as an ordered pair) of the equation above. Reduce all fractions to lowest terms.
Slope:
y-intercept:
Answers
Members of a bowling league play thousands of combined games over the course of a season. Suppose that the scores of individual games have a known standard deviation of σ=30 pins. Isla plans on taking a random sample of n games from this population to make a 95% confidence interval for the mean score. She wants the margin of error to be no more than 10 pins. Which of these is the smallest approximate sample size required to obtain the desired margin of error?
9 games
30 games
35 games
43 games
55 games
Answers
Answer: 35
Step-by-step explanation:
Got it right on khan
Give the domain and range. On a coordinate plane, points are at (negative 2, negative 1), (0, 1), (2, 3). a. domain: {2, 0, 2}, range: {1, 1, 3} b. domain: {–1, 1, 3}, range: {–2, 0, 2} c. domain: {–2, 0, 2}, range: {–1, 1, 3} d. domain: {1, 1, 3}, range: {2, 0, 2} Please select the best answer from the choices provided A B C D
Answers
Answer:
c. domain: {-2, 0, 2}, range: {-1, 1, 3}
Step-by-step explanation:
From the given points (negative 2, negative 1), (0, 1), (2, 3), we can determine the domain and range.
The domain represents the set of all possible x-values of the points, and the range represents the set of all possible y-values of the points.
In this case, we can see that the x-values are -2, 0, and 2, and the corresponding y-values are -1, 1, and 3.
Therefore, the correct answer is:
c. domain: {-2, 0, 2}, range: {-1, 1, 3}
For the function in the graph, identify the values of f(0), f(2), and f(−3).
−2; 2; −5
2; 0; −4
−2; 0; −5
2; −2; −4

Answers
Option C: −2; 0; −5
This is about interpreting graph coordinates.
The point f(0) is simply the value of y when x = 0. This is the y - intercept.From the graph, this value is y = -2
The point f(2) is simply the value of y when x = 2. From the graph, when x = 2, we see that y = 0 because this is the x - coordinate. The point f(-3) is simply the value of y when x = -3. From the graph, when x = -3, we see that the corresponding value of y = -5.Thus;
f(0) = -2
f(2) = 0
f(-3) = -5
Read more at; brainly.com/question/4533534
Which expressions will help you find the surface area of this right triangular prism? Select all that apply.
38 × 45
1/2 × 36 × 45
45 × 36
1/2 × 36 × 38

Answers
How many significant figures are in the number
43.6? 43.6 has [?] significant figures.
Answers
Answer:
43.6 has 3 significant figures.
Which is equivalent to 80 Superscript one-fourth x? (StartFraction 80 Over 4 EndFraction) Superscript x RootIndex 4 StartRoot 80 EndRoot Superscript x RootIndex x StartRoot 80 EndRoot Superscript 4 (StartFraction 80 Over x EndFraction) Superscript 4
whoever can answer this gets brainliest
Answers
The expression that is equivalent to \(80^{(1/4}\) * x is \(80^{4/x}\)
How to calculate the valueTo determine the equivalent expression to \(80^{1/4}\) * x, let's analyze each option:
\(80/4^{x}\)
This expression simplifies to \(20^{x}\), but it is not equivalent to the original expression.
Applying the power of a power rule, this expression simplifies to \(80^{x/4}\) , which is not equivalent to the original expression.
\(80/x^{4}\)
This expression can be simplified as \(80^{4 x^{4} }\) , which is not equivalent to the original expression.
Therefore, the expression that is option d.
Learn more about expressions on
https://brainly.com/question/723406
#SPJ1
Point P is the incenter of triangle ABC,
PZ = 7 units, and PA = 12 units
Answers
The incircle centered at point P has a radius of 7 units.
What is the radius of incircle?Here given that,
PA = 12 units.
PZ = 7 units
We are told that point P is the incenter of the triangle and the center of the triangle's incircle. The incircle is the largest circle that can be formed in a triangle and is tangent to all three sides. The circle's radius will be a perpendicular line from point P to any side of the triangle. PZ = PY = PX in the triangle shown, and each value equals the radius of the circle.As a result, no additional calculations are required for this problem because we already know that PZ = 7 units, resulting in the radius, r = 7 units.The complete question is :
"Point P is the incenter of triangle ABC, PZ = 7 units, and PA = 12 units.
The radius of the incircle centered at point P is ? units."
To learn more about incenter radius refer to :
https://brainly.com/question/1511303
#SPJ1
In which direction does the parabola x=2y2+1 open?
A up
B down
C Right
D left
Answers
Answer and Step-by-step explanation:
First, we need to set this equation equal to y, which means we need to get y by itself, and all other terms equal to y.
x = \(2y^2 + 1\)
Subtract 1, then divide by 2 on both sides.
\(x - 1 = 2y^2\\\\\frac{x-1}{2} = y^2\)
Now, take the square root of both sides.
\(y=\sqrt{\frac{x-1}{2}}\)
We see that the value with the x (1) is positive, and that we have a square root function, which means the parabola would open to the right.
(If the x value was negative, the square root function's parabola would open to the left)
So, C (Right) is the correct answer.
#teamtrees #PAW (Plant And Water)
I hope this helps!
Prove that "If α is an ordinal and β ∈ α, then β is an ordinal" ?
Answers
If α is an ordinal and β ∈ α, then β satisfies all three properties of an ordinal. Therefore, β is also an ordinal.
To prove the statement "If α is an ordinal and β ∈ α, then β is an ordinal," we need to demonstrate that if α is an ordinal and β is an element of α, then β satisfies the three properties of an ordinal:
Well-Ordering: Every element of β is strictly well-ordered by the membership relation ∈. This property holds because α is an ordinal and satisfies the well-ordering property, and β being an element of α inherits this property.
Transitivity: For any two elements γ and δ in β, if γ ∈ δ and δ ∈ β, then γ ∈ β. Since β is an element of α and α is transitive, the transitivity property carries over to β.
Trichotomy: For any two elements γ and δ in β, either γ ∈ δ, δ ∈ γ, or γ = δ. Again, this property is inherited from α, as β is an element of α.
For more such questions on ordinal
https://brainly.com/question/30648205
#SPJ8
What is the next number 7,11,2,18,-7?
Answers
Answer:
57
Step-by-step explanation:
x - (-7) = 64
x + 7 = 64
x = 64 - 7
x = 57
Find the measures of the indicated angles.

Answers
Step-by-step explanation:
first, find the value of angle t
angles of a triangle add up to 180.
with this, we can set up the equation
180 = t + 62 + 56
t = 62
to find angle w, find the sum of the top angles
25 + 56 = 81
again, sum of angles in a triangle adds to 180.
since we have the bottom right angle and the top angle, we can find the bottom left angle
180 = 56 + 62 + w
w = 37
finally we can find angle v
180 = 25 + w + v
180 = 25 + 37 + v
v = 118
another approach would be to find angle v after finding angle t.
because the two angles are supplementary, they add up to 180
angle v + angle w = 180
Suppose that R is the finite region bounded by y=x,y=x+1,x=0, and x=3. Find the exact value of the volume of the object we obtain when rotating R about the x-axisV=
Answers

PLEASE HELP
I need this done is 13 minutes.
Polygon ABCD with vertices at A(1,-1) B(3,-1), C(3,-2) and D(1-2) is dilated to create polygon ABCD with vertices at A’(2,-2), B(6,-2), C’(6,-4) and D’(2,-4). Determine the scale factor used to create the image
A. 3
B. 2
C. 1/2
D. 1/3
Answers
The correct answer is B. 2, as the scale factor used to create the dilated polygon is 2.
To determine the scale factor used to create the image, we can compare the corresponding side lengths of the original polygon ABCD and the dilated polygon A'B'C'D'.
Let's calculate the lengths of the corresponding sides:
Side AB: The length of side AB is 3 - 1 = 2 units in the original polygon. In the dilated polygon, the length of side A'B' is 6 - 2 = 4 units.
Side BC: The length of side BC is -2 - (-1) = -1 units in the original polygon. In the dilated polygon, the length of side B'C' is -4 - (-2) = -2 units.
Side CD: The length of side CD is 1 - 3 = -2 units in the original polygon. In the dilated polygon, the length of side C'D' is 2 - 6 = -4 units.
Side DA: The length of side DA is -1 - (-2) = 1 unit in the original polygon. In the dilated polygon, the length of side D'A' is -2 - (-4) = 2 units.
Now, let's compare the corresponding side lengths:
AB: A'B' = 4 units / 2 units = 2
BC: B'C' = -2 units / -1 units = 2
CD: C'D' = -4 units / -2 units = 2
DA: D'A' = 2 units / 1 unit = 2
The scale factor used to create the image is the ratio of the corresponding side lengths.
In this case, all the corresponding side lengths have a ratio of 2.
For similar question on scale factor.
https://brainly.com/question/30581940
#SPJ8
HELP PLEASE I’m having troubles!!!
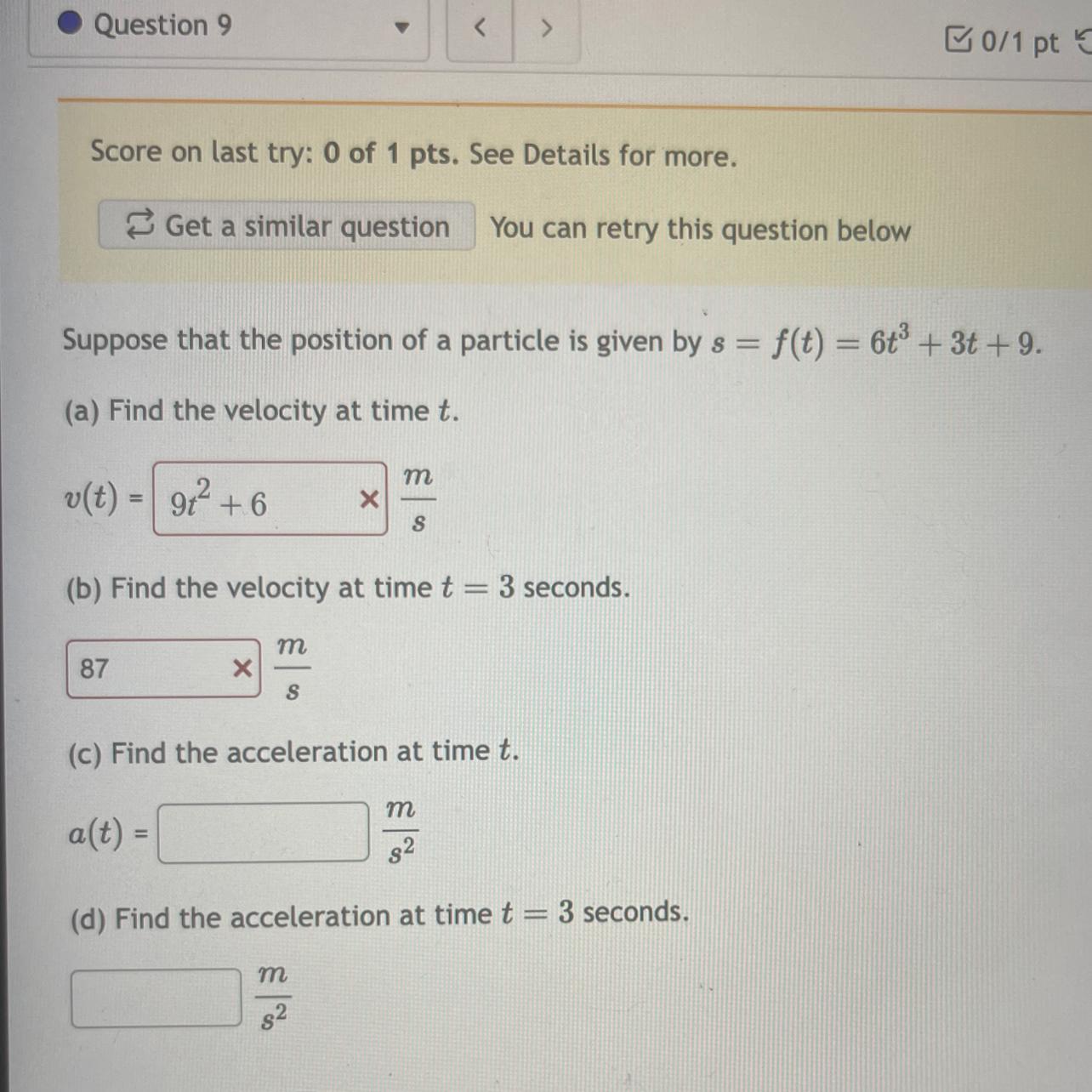
Answers
1. The velocity at time t , v(t) = (18t² + 3 ) m/s
2. The velocity at time t = 3 seconds = 165 m/s
3. The acceleration at time t, a(t) =( 36t )m/s²
4. The acceleration at time t = 3 seconds = 108 m/s²
What is instateanou velocity and acceleration?The quantity that tells us how fast an object is moving anywhere along its path is the instantaneous velocity.
Instantaneous acceleration is defined as the ratio of change in velocity during a given time interval such that the time interval goes to zero.
1. s(t) = 6t³ + 3t +9
to find the velocity at time t, we differentiate s(t)
= 18t² + 3
2. at t = 3s
= 18(3)² +3
= 165 m/s²
3. v(t) = 18t² + 3
to get the acceleration at time t, we differentiate v(t)
= 36t
4. when t = 3
a = 36 × 3
= 108 m/s²
learn more about instantaneous velocity and acceleration from
https://brainly.com/question/2234298
#SPJ1
I need help I can’t find the anwer please help

Answers
Answer:
You: 3, 6, 9, 12
Friend:4, 8, 12, 16
Step-by-step explanation:
You/Friend ratio is 3/4
Missing numbers:
8 / (4/3) = 612 * (4/3) = 16Numbers:
You 3, 6, 9, 12
Friend 4, 8, 12, 16
Find the value of x such that the line containing (1,2) and (5,3) is perpendicular to the line containing (x,4) and (3,0)
Answers
The value of x that makes the line containing (1,2) and (5,3) perpendicular to the line containing (x,4) and (3,0) is x = 2.
To determine the value of x such that the line containing (1,2) and (5,3) is perpendicular to the line containing (x,4) and (3,0), we need to find the slope of both lines and apply the concept of perpendicular lines.
The slope of a line can be found using the formula:
slope = (change in y) / (change in x)
For the line containing (1,2) and (5,3), the slope is:
slope1 = (3 - 2) / (5 - 1) = 1 / 4
To find the slope of the line containing (x,4) and (3,0), we use the same formula:
slope2 = (0 - 4) / (3 - x) = -4 / (3 - x)
Perpendicular lines have slopes that are negative reciprocals of each other. In other words, if the slope of one line is m, then the slope of a line perpendicular to it is -1/m.
So, we can set up the equation:
-1 / (1/4) = -4 / (3 - x)
Simplifying this equation:
-4 = -4 / (3 - x)
To remove the fraction, we can multiply both sides by (3 - x):
-4(3 - x) = -4
Expanding and simplifying:
-12 + 4x = -4
Adding 12 to both sides:
4x = 8
Dividing both sides by 4:
x = 2
For more such questions on line.
https://brainly.com/question/280216
#SPJ8
To apply Central Limit Theorem on sample proportions in One Sample Proportion test, the sample size and the population proportion under null hypothesis need to satisfy certain conditions. Which of the following scenarios meet the requirement?
A. The sample size is 50 and the population proportion under null hypothesis is 25%.
B. The sample size is 70 and the population proportion under null hypothesis is 90%.
C. The sample size is 50 and the population proportion under null hypothesis is 15%.
D. The sample size is 200 and the population proportion under null hypothesis is 4%.
Answers
Answer:
The sample size is 50 and population proportion under null hypothesis is 25% ( A ) meets the requirement
Step-by-step explanation:
when applying the central limit theorem on sample proportions in one sample proportion test .The conditions needed to be satisfied are np > 10, and n( 1-p ) > 10
A) sample size ( n ) = 50
population proportion = 25%
np = 50 * 0.25 = 12.5 which is > 10 ( 1st condition met )
n( 1 - p ) = 50( 1 - 0.25 ) = 37.5 which is > 10 ( second condition met )
B ) sample size (n) = 70
population proportion = 90%
np = 70*0.9 = 63 which is > 10 ( 1st condition met )
n(1-p) = 70 ( 1 - 0.9 ) = 7 which is < 10 ( second condition not met )
C) sample size ( n ) = 50
population proportion = 15% = 0.15
np = 50 * 0.15 = 7.5 which is < 10 ( 1st condition not met )
n ( 1 - p ) = 50 ( 1 - 0.15 ) = 50 * 0.85 = 42.5 which is > 10 ( second condition met )
D) sample size ( n ) = 200
population proportion = 4% = 0.04
np = 200 * 0.04 = 8 which is < 10 ( 1st condition not met )
n ( 1 - p ) = 200 ( 1 - 0.04 ) = 192 which is > 10 ( second condition met )
hence : The sample size of 50 with population proportion under null hypothesis of 25% meets the requirement
two positive intergers have a product of 50 one interger is twice the other . what are the intergers
Answers
Answer:
10 and 5.
Step-by-step explanation:
Let the integers be x and y.
xy = 50
x = 2y
Put x as 2y in the first equation.
(2y)y = 50
2y² = 50
y² = 50/2
y² = 25
y = √25
y = 5
Put y as 5 in the second equation.
x = 2(5)
x = 10
