!!WILL MARK BRAINLIEST!! Write in slope-intercept form an equation of the line that passes through the given points.

Answers
Answer:
y = 1/4x
Step-by-step explanation:
First find the slope
m = (y2-y1)/(x2-x1)
= (2-1)/(8-4)
= 1/4
The slope intercept form of a line is
y = mx+b
where m is the slope and b is the y intercept
y = 1/4x +b
Substitute a point into the equation
1 = 1/4(4) +b
1 = 1+b
b= 0
y = 1/4x
Related Questions
Find m/TRS if m/1 = 2x + 4 and
m/2= 3x - 3.
T
P
S
1
R

Answers
If the angles are ∠1 = 2x + 4 and ∠2 = 3x - 3, then m∠TRS = 36°.
What is an angle?
An angle is a figure in plane geometry that is created by two rays or lines that have a shared endpoint. The Latin word "angulus," which meaning "corner," is the source of the English term "angle." The shared terminus of two rays is known as the vertex, and the two rays are referred to as sides of an angle.
The measure of ∠1 = 2x + 4
The measure of ∠2 = 3x - 3
The measure of ∠TRS is -
∠TRS = ∠1 + ∠2
Since, PR is a bisector then ∠1 = ∠2.
The equation is -
2x + 4 = 3x - 3
2x - 3x = - 3 - 4
-x = -7
x = 7
Substitute the value of x in the angles -
∠1 = 2(7) + 4
∠1 = 14 + 4
∠1 = 18°
∠2 = 3(7) - 3
∠2 = 21 - 3
∠2 = 18°
So, the value of ∠TRS is -
∠1 + ∠2
18° + 18°
36°
Therefore, the measure of ∠TRS is 36°.
To learn more about angle from the given link
https://brainly.com/question/25716982
#SPJ1
Which expression is equivalent to 3(2x + 4)?
A) 5x + 7
B) 6x + 7
C) 6x + 12
D) 5x + 12
Answers
Answer:
C) 6x + 12
Step-by-step explanation:
3 × 2x = 6x
3 × 4 = 12
Aaron kept $12 000 in a bank account with an annual interest rate of 4%. After exactly 2 years, the bank chose Aaron as the winner for a prize money worth $5000. Aaron decided to invest all his savings and the prize money into a Trust Fund which offers a dividend of 4.5% per annum. When ( which year ) will all his investment value exceed $20 000?
Answers
Answer:
Initial amount P = $12000
Interest after 2 years I = 4%*2 = 8%
Investment into Trust fund:
$12000 + $5000 + 0.08*$12000 = $17960Interest amount to exceed $20000:
$20000 - $17960 = $2040Time required to get $2040:
17960*0.045x = 2040808.2x = 2040x = 2040/808.2x = 2.52 yearsThe investment will exceed $20000 in the second half of the third year
a line with slope 2 intersects a line with slope 6 at the point (40, 30). what is the distance between the x-intercepts of these two line
Answers
The distance between the x-intercepts of these two line is 10 units.
Given that,
These two lines' x-intercepts are separated by 10 units.
Equation of the line with slope 2 is
y-30/x-40 = 2
For x intercept put y = 0,
then
-30/x-40 =2
x =25
Equation of the line with slope 6 is
y-30/x-40 =6
For x intercept put y = 0,
then
-30/x-40 =6
x =35
Distance between x-intercepts of these two lines is difference of the two intercepts i.e,
D = 35-25 = 10.
Thus, the distance between the x-intercepts of these two line is 10 units.
To learn more about x-intercepts click here:
brainly.com/question/14180189
#SPJ4
please help :D I forgot how to do this, I need all the parts

Answers
Answer:
question 1 the answer would be 4/10
question 2 the answer would be tails 1/2 and green 1/10
question 3 the answer would be 3/9 or 1/3
question 4 the answer would be yellow 2/10 or 1/5 and blue would be 3/10
Step-by-step explanation:
solve 3x by 4 - 2x+5 by 3 = 5 by 2
Answers
Answer:
50
Step-by-step explanation:
The given equation is,
→ 3x/4 - (2x + 5)/3 = 5/2
→ 3x × 3 - 4(2x +5)/12 = 5/2
→ 9x - 8x -20/12 = 5/2
→ (x - 20)/12 = 5/2
→ x - 20 / 6 = 5
→ x - 20 = 30
→ x = 20 + 30
→ x = 50
• Hence the value of x is 50 .Answer:
x=50
Step-by-step explanation:
plsssssssssss help me

Answers
Answer: 40
Step-by-step explanation:
38+ 52=90
230-90=40
-5 = -y - 3x
Write the equation in slope-intercept form. Please help me. :)
Answers
Answer:
y = -3x + 5
Step-by-step explanation:
You want it in y = mx + b form
-5 = -y - 3x
Add y to both sides
-5 + y = -y + y - 3x
-5 + y = -3x
Add 5 to both sides
- 5 + 5 + y = -3x + 5
y = -3x + 5
Ms. Charles asked her students how many minutes they spent studying for a test the night before the test was given. She found that the time students spent studying and their test scores had a positive correlation. Which scatterplot below shows this relationship?

Answers
Answer:
Option A
Step-by-step explanation:
C and D are scattered showing no pattern, Therefore, it is either A or B. I say it's not B due the the fact more studying minutes made even less test grades. So A is the only option left.
Find the zeros for the following function:F(x) = x^2 − 9x − 36
Answers
The zero of the given function is x = 12 and. -3
Zeros of a functionGiven the function expressed below;
F(x) = x^2 − 9x − 36
The zero of the function is the. point where f(x) = 0
x^2 − 9x − 36 = 0
Factorize to have;
x^2-12x+3x-36=0
X(x-12)+3(x-12)=0
(x-12)(x+3)= 0
Determine the zeros
x = 12 and. -3
Hence the zero of the given function is x = 12 and. -3
Learn more on zero of a function here; https://brainly.com/question/65114
#SPJ1
divide t by s, then multiply 6 by the result
Answers
hello
to solve this question, we just have to follow thr instructions as it is
\(\frac{t}{s}\times6=\frac{6t}{s}\)the answer to this question is 6t/s
The rectangular waiting area for a popular amusement park ride is covered by a large sun canopy. The total area of the canopy, in square feet, is 100 square feet more than twice the area where guests wait.
Which equation could you use to find the area of the place where guests wait for the ride if the area of the canopy is 7,600 square feet?

Answers
The equation which can be used to find the area of the place where guests wait for the ride if the area of the canopy is 7600 square feet is:
2a+100=7600.
Given, The rectangular waiting area for a popular amusement park ride is covered by a large sun canopy.
The total area of the canopy, in square feet, is 100 square feet more than twice the area where guests wait.
let the area of the place where guests wait be represented by 'a'.
the canopy covers the area = 2a + 100
total area of the canopy = 7600
equation used to find the area of the place where guests wait for the ride if the area of the canopy is 7,600 square feet = ?
⇒ 2a + 100 = 7600
arrange the like terms.
⇒ 2a = 7600 - 100
calculate the difference.
⇒ 2a = 7500
⇒ a = 7500/2
⇒ a = 3750
Hence the area of the place where guests wait is 3750 square feet.
Learn more about Linear equations here:
brainly.com/question/26310043
#SPJ1
Determine if the following discrete-time systems are causal or non-causal, have memory or are memoryless, are linear or nonlinear, are time-invariant or time-varying. Justify your answers. a) y[n]=x[n]+2x[n+1] b) y[n]=u[n]x[n] c) y[n]=∣x[n]∣. d) y[n]=∑i=0n(0.5)nx[i] for n≥0
Answers
a) Causal, memoryless, linear, time-invariant.
b) Causal, memoryless, linear, time-invariant.
c) Causal, memoryless, nonlinear, time-invariant.
d) Causal, has memory, nonlinear, time-invariant.
a) The system described by y[n] = x[n] + 2x[n+1] is causal because the output value at any time index n only depends on the current and past input values. It is memoryless since the output at a given time index n does not depend on any past or future inputs. The system is linear because the output is a linear combination of the input values. It is also time-invariant because the system's behavior remains unchanged over time.
b) The system y[n] = u[n]x[n] is causal since the output at any time index n only depends on the current and past input values. It is memoryless because the output at a given time index n does not depend on any past or future inputs. The system is linear because the output is a product of the input signal and a constant. It is also time-invariant because the system's behavior remains unchanged over time.
c) The system y[n] = |x[n]| is causal since the output at any time index n only depends on the current and past input values. It is memoryless because the output at a given time index n does not depend on any past or future inputs. The system is nonlinear because the absolute value operation is a nonlinear operation. It is time-invariant because the system's behavior remains unchanged over time.
d) The system y[n] = ∑(0.5)^n x[i] for i=0 to n is causal since the output at any time index n only depends on the current and past input values. It has memory because the output at a given time index n depends on all past input values up to the current time index. The system is nonlinear because the output is a sum of terms raised to a power, which is a nonlinear operation. It is time-invariant because the system's behavior remains unchanged over time.
Learn more About time-invariant from the given link
https://brainly.com/question/13266890
#SPJ11
1.2192 rounded to the nearest hundred
Answers
Answer:
1.22
Step-by-step explanation:
Find two consecutive even integers whose sum is 26.
Answers
Answer:
4k+2 (when k=6)
5k+6 (when k=4)
Step-by-step explanation:
Answer:
14
12
Step-by-step explanation:
Just run through possible even numbers up till 26.
14 + 12 = 26 and they are two consecutive even numbers
is the displacement of an object during a specific unit of time.
Hey if you can answer this correct and you can do more answers i can keep on giving you more points do it fast because i on a unit test im doing home school thanks
Answers
Answer:
Velocity
Step-by-step explanation:
Velocity is the displacement of an object during a specific unit of time
Answer:
Velocity
Step-by-step explanation:
4+(-2) =
-5 + ( -5 ) =
Answers
-10 ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
Answer:
4+(-2) = 2
-5+(-5)=-10
Step-by-step explanation:
The triangles below are similar. Which similarity statement expresses the relationship between the two triangles?

Answers
Answer:
C. ΔFGH~ΔJKL
Step-by-step explanation:
Find the value of x.
O x = 2
O x = 3
Ox=33
O x = 52

Answers
Answer:
x=3
Step-by-step explanation:
i just know
if the original quantity is 8 and the new quantity is 4 what is the percent decrease
Answers
Answer:
50% decrease
Step-by-step explanation:
it would be a 50% decrease because half of 8 is 4 and 1/2 is 50 %.
please solve this question
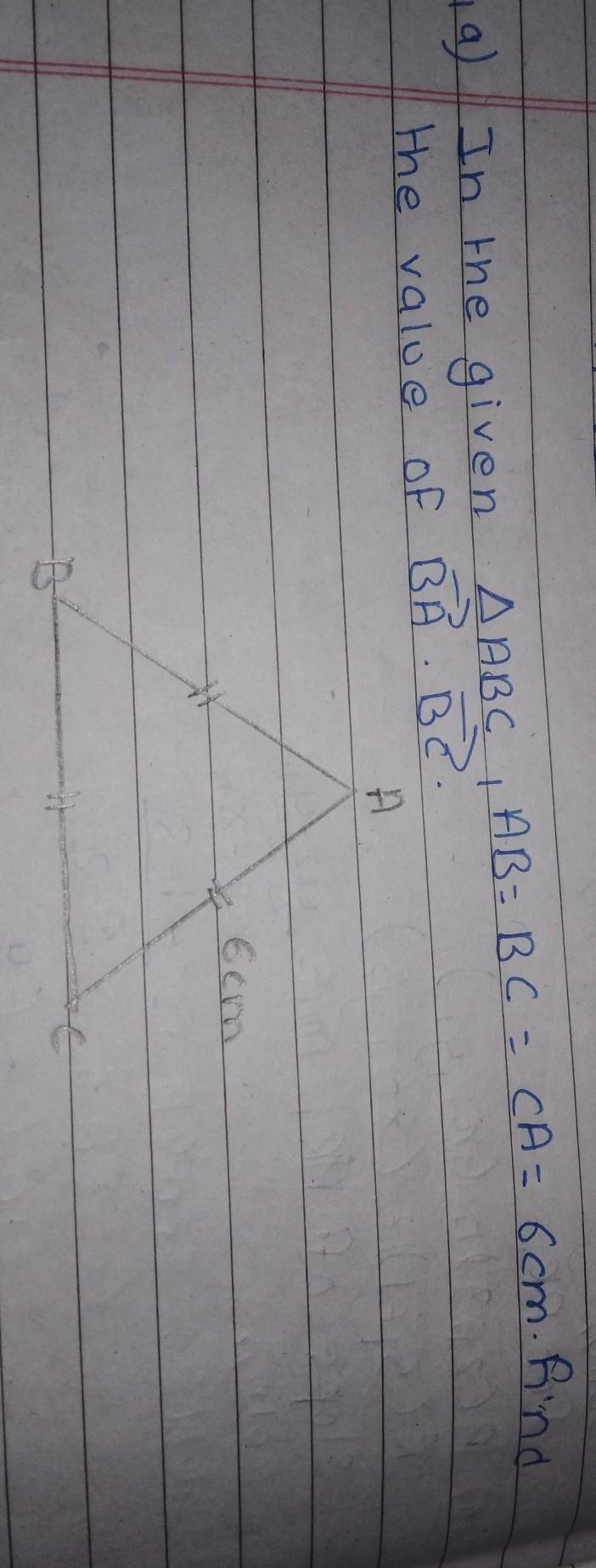
Answers
The value of BA.BC vector is 18 cm² as side lengths are 6 cm.
What is triangle?A triangle is a closed two-dimensional geometric figure with three sides, three angles, and three vertices. It is one of the basic shapes in geometry and is formed by connecting three non-collinear points with straight line segments. The sum of the interior angles of a triangle is always 180 degrees, and there are various types of triangles, such as equilateral, isosceles, scalene, right-angled, acute-angled, and obtuse-angled triangles. Triangles are used in a wide range of applications, from architecture and engineering to physics and computer graphics.
Here,
To find the area of the AABC, we can use Heron's formula:
s = (AB + BC + CA)/2 = (6 + 6 + 6)/2 = 9
Area = √(s(s-AB)(s-BC)(s-CA))
= √(9(9-6)(9-6)(9-6))
= 27/4 cm²
To find the height of the AABC corresponding to side AB, we can use the formula:
Area = 1/2 * AB * height
Rearranging, we get:
height = 2 * Area / AB = 2 * 27/4 / 6 = 9/4 cm
Therefore, the area of AABC is 27/4 cm², and the height corresponding to side AB is 9/4 cm.
For the second part of the question, we can use the Law of Cosines to find the angle between sides BA and BC:
cos(A) = (BA² + BC² - CA²) / (2 * BA * BC)
= (6² + 6² - 6²) / (2 * 6 * 6)
= 1/2
A = arccos(1/2) = 60 degrees
Using this angle, we can find the length of side BA . BC:
BA . BC = 2 * AB * BC * cos(A)
= 2 * 6 * 6 * cos(60)
= 18 cm²
Therefore, BA . BC = 18 cm²
To know more about triangle,
https://brainly.com/question/28600396
#SPJ1
-7x-8=-10x+4 pls help me
Answers
Answer:
X= 4
Step-by-step explanation:
Answer:
x=4
Step-by-step explanation:
-7x - 8 = -10x + 4
-7x - 8 + 10x = 4 ( add 10x to the left side and subtract 10x from the right)
3x - 8 = 4 ( add -7x and 10x to get 3x)
3x = 4 + 8 ( add 8 to the right and subtract 8 from the left)
3x = 12 ( add 4 and 8 to get 12 )
\(\frac{3x}{3}\) = \(\frac{12}{3}\) ( divide both sides by 3 )
x = 4
The answer is x =4
HOPE THIS HELPED
**Spam answers will not be tolerated**
Please evaluate the Derivative using the Limit Process. Show all workings.

Answers
Answer:
\(\displaystyle f'(x)=-\frac{2}{x^{{}^{3}\!/\!{}_{2}}}\)
Step-by-step explanation:
We have the function:
\(\displaystyle f(x)=\frac{4}{\sqrt x}\)
And we want to find the derivative using the limit process.
Recall that the definition of a derivative is:
\(\displaystyle \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\)
Therefore, by substitution:
\(\displaystyle \lim_{h \to 0}\frac{\dfrac{4}{\sqrt{x+h}}-\dfrac{4}{\sqrt x}}{h}\)
First and foremost, we can move the constant factor outside of the limit:
\(\displaystyle =\lim_{h \to 0}\frac{4\left(\dfrac{1}{\sqrt{x+h}}-\dfrac{1}{\sqrt x}\right)}{h}\\ \\=4\lim_{h \to 0}\frac{\dfrac{1}{\sqrt{x+h}}-\dfrac{1}{\sqrt x}}{h}\)
Next, we can multiply everything by (√(x + h)(√x) to eliminate the fractions in the denominator. Therefore:
\(\displaystyle =4\lim_{h \to 0}\frac{\dfrac{1}{\sqrt{x+h}}-\dfrac{1}{\sqrt x}}{h}\left(\frac{\sqrt{x+h}\sqrt x}{\sqrt{x+h}\sqrt x}\right)\)
Distribute:
\(\displaystyle =4\lim_{h \to 0}\frac{\left({\sqrt{x+h}\sqrt x}\right)\dfrac{1}{\sqrt{x+h}}-(\sqrt{x+h}\sqrt x)\dfrac{1}{\sqrt x}}{h({\sqrt{x+h}\sqrt x})}\)
Distribute and simplify:
\(\displaystyle =4 \lim_{h\to 0}\frac{\sqrt x-\sqrt{x+h}}{h(\sqrt{x+h}\sqrt{x}) }\)
Next, we can multiply both sides by the conjugate of the numerator. In other words, multiply by (√x + √(x + h)). Thus:
\(\displaystyle = 4\lim_{h\to 0}\frac{\sqrt x-\sqrt{x+h}}{h(\sqrt{x+h}\sqrt{x}) }\left(\frac{\sqrt x +\sqrt{x+h}}{\sqrt x +\sqrt{x+h}\right)}\)
Simplify:
\(\displaystyle =4 \lim_{h \to 0} \frac{x-(x+h)}{h(\sqrt{x+h}\sqrt x)(\sqrt x+\sqrt{x+h})}\\ \\ \\ =4 \lim_{h \to 0} \frac{x-x-h}{h(\sqrt{x+h}\sqrt x)(\sqrt x+\sqrt{x+h})} \\ \\ \\=4 \lim_{h \to 0} \frac{-h}{h(\sqrt{x+h}\sqrt x)(\sqrt x+\sqrt{x+h})}\)
Cancel like terms:
\(\displaystyle =4 \lim_{h \to 0} -\frac{1}{(\sqrt{x+h}\sqrt x)(\sqrt x+\sqrt{x+h})}\)
Now, we can use direct substitution. Hence:
\(\displaystyle \Rightarrow4 \left( -\frac{1}{(\sqrt{x+0}\sqrt x)(\sqrt x+\sqrt{x+0})}\right)\)
Simplify:
\(\displaystyle =4\left( -\frac{1}{(\sqrt{x}\sqrt x)(\sqrt x+\sqrt{x})}\right) \\ \\ \\ =4\left( -\frac{1}{(x)(2\sqrt{x})}\right)\)
Multiply:
\(\displaystyle =- \frac{4}{2x\sqrt{x}}\)
Reduce and rewrite:
\(\displaystyle =-\frac{2}{x(x^{{}^{1}\! / \! {}_{2} \!})}\)
Simplify:
\(\displaystyle =-\frac{2}{x^{{}^{3}\!/\!{}_{2}}}\)
Therefore:
\(\displaystyle f'(x)=-\frac{2}{x^{{}^{3}\!/\!{}_{2}}}\)
Please help I have been stuck for a while now

Answers
Un depósito de agua en forma de cono invertido tiene un altura de 12 pies y de diámetro 8 pies. Si al deposito le entra agua a razón de 6 m/min. Determinar a qué velocidad crece el nivel del agua cuando la profundidad de esta es de 6 metros.
Answers
The water level rises at a rate of 3/(2π) meters per minute when the depth is 6 meters.
How to solveTo find the rate at which the water level rises when the depth is 6 meters in an inverted conical reservoir, follow these steps:
Convert dimensions to meters: height H = 3.6576 m, radius R = 1.2192 m.
Express the radius of the water surface (r) in terms of water height (h): r = (1/3)h.
Write the volume formula (V) in terms of h: V = (1/27)πh³.
Differentiate with respect to time (t): dV/dt = (1/27)π(3h²)(dh/dt).
Plug in given values (dV/dt = 6 m³/min, h = 6 m): 6 = (1/27)π(108)(dh/dt).
Solve for dh/dt: dh/dt = 3/(2π) meters per minute.
The water level rises at a rate of 3/(2π) meters per minute when the depth is 6 meters.
Read more about water level here:
https://brainly.com/question/30015788
#SPJ1
The question in English
A reservoir in the shape of an inverted cone has a height of 12 feet and a diameter of 8 feet. If water enters the tank at a rate of 6 m/min. Determine how fast the water level rises when its depth is 6 meters.
the supplement of an angle is 6* less than it's complement . find the angle.
Answers
Step-by-step explanation:
you mean it is 6° less, right ?
supplement means together they have 180°.
complement means together they have 90°.
x is our angle.
180 - x is the supplement angle.
90 - x is the complement angle.
180 - x = 90 - x - 6
90 = -6
you see, that is not possible.
the difference between the supplementary angle and the complementary angle is always 90°.
e.g.
x = 30°
supplement = 180-30 = 150°
complement = 90-30 = 60°
the difference is : 150 - 60 = 90°
x = 80°
supplement = 180 - 80 = 100°
complement = 90-80 = 10°
the difference is : 100 - 10 = 90°
and so on.
so, again, there is no angle that satisfies that criteria.
either you made a mistake in the problem description, or your teacher tried to be tricky.
remember, as x has also a complementary angle, it must be smaller than 90°.
so, the supplementary angle of x must be larger than 90°, and therefore larger than the complementary angle.
there is no angle, for which the supplementary angle is smaller than the complementary angle.
The sun came out and the temperature quickly rose 18 degrees. the a thunderstorm hits and the temperature drops 6 degrees. the sun comes back out the temperature raises 12 degrees. the temperature is now 94 degrees. what was the starting temperature?
Answers
By solving a linear equation we will see that the initial temperature was 66 degrees.
What was the initial temperature?
Let's define T as the initial temperature.
First, it increases by 18 F, then it decreases 6 F, and finally, it increases another 12 F, such that the end temperature is 94F.
Then we can write:
T + 18F - 6F + 12F = 94F
Now we can solve that linear equation to find T.
T = 94F - 18F + 6F - 12 F = 66 F
In this way, we conclude that the initial temperature was 66 degrees.
If you want to learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
Tanisha left her house at time zero and drove to the store, which is 8 blocks away, at a speed of 4 blocks per minute. Then she stopped and went into the store for 3 minutes. From there, she drove in the same direction at a speed of 3 blocks per minute until she got to the bank, which is 12 blocks away from the store. She stopped at the bank for 7 minutes. Then she drove home at a speed of 5 blocks every 2 minutes. Make a graph of showing the number of blocks away from home that Tanisha is xx minutes after she leaves her house, until she gets back home.
Answers
This prompt is about being able to represent time and distance on a graph called Distance-Time Graph. See the graph attached.
What is a Distance-Time Graph and why is it important?
A Distance-Time Graph is a sort of graph that depicts the relationship between distance and time for a moving object.
It is a handy tool for studying an object's motion since it allows one to simply ascertain the object's speed and acceleration. It is also significant because it gives a visual depiction of an object or subject's motion, making the underlying physical ideas easier to grasp.
Learn more about Distance - Time Graph:
https://brainly.com/question/29747583
#SPJ1
Full Question:
Tanisha left her house at time zero and drove to the store, which is 8 blocks away, at a speed of 4 blocks per minute. Then she stopped and went into the store for 3 minutes. From there, she drove in the same direction at a speed of 3 blocks per minute until she got to the bank, which is 12 blocks away from the store. She stopped at the bank for 7 minutes. Then she drove home at a speed of 5 blocks every 2 minutes. Make a graph of showing the number of blocks away from home that Tanisha is xx minutes after she leaves her house, until she gets back home.
Make a graph of showing the number of blocks away from home that Tanisha is x minutes after she leaves her house, until she gets back home.

Find a formula for a geometric sequence that begins 81, 54, 36,...
Answers
The formula for the geometric sequence that begins with the terms 81, 54, 36, and so on is:
aₙ = 81 * (1/3)^(n-1)
To find a formula for a geometric sequence that begins with the terms 81, 54, 36, and so on, we need to determine the common ratio between consecutive terms.
By observing the sequence, we can see that each term is obtained by dividing the previous term by 3. Hence, the common ratio is 1/3.
Let's denote the first term as a₁ and the common ratio as r.
a₁ = 81 (the first term)
r = 1/3 (the common ratio)
The general formula for a geometric sequence is given by:
aₙ = a₁ * r^(n-1)
where aₙ represents the nth term of the sequence.
Substituting the values we have:
aₙ = 81 * (1/3)^(n-1)
The formula for the geometric sequence that begins with the terms 81, 54, 36, and so on is:
aₙ = 81 * (1/3)^(n-1)
Using this formula, you can find any term in the sequence by substituting the corresponding value of n.
For example, to find the 5th term of the sequence, you would substitute n = 5 into the formula:
a₅ = 81 * (1/3)^(5-1)
a₅ = 81 * (1/3)^4
a₅ = 81 * (1/81)
a₅ = 1
The 5th term of the sequence is 1.
For more questions on geometric sequence
https://brainly.com/question/24643676
#SPJ8
Xavier Knox's annual salary is $61,100. He is paid semimonthly. His personal exemptions total $4,000. How
much does his employer deduct from each of Knox's paychecks for state income tax of 3.5 percent?
a. $166.54
c.
b. $83.27
$83.13
d. $166.26
Answers
The amount that Xavier Knox's employer deducts from his paychecks for state income tax is b. $83.27
How to find the state income tax?First find his taxable income:
= Annual salary - Personal exemptions
= 61, 100 - 4, 000
= $57, 100
The state income tax per year is:
= 57, 100 x 3.5% state income tax rate
= $1, 998.50
The semimonthly state income tax deducted is:
= 1, 998.50 / (12 months x twice a month)
= $83.27
In conclusion, on a semimonthly basis, $83.27 is deducted for state income tax.
Find out more on state income tax at https://brainly.com/question/23687799
#SPJ1