Will and Ben win £1000 in a raffle
they give a fifth of it to charity and share what's left in the ratio 1:3.
How much is bens share
Answers
Answer:
600
Step-by-step explanation:
Answer:
£600
Step-by-step explanation:
1/5 of 1000= £200
that means £800 is left over
1:3= 200:600
ben gets £600, will gets £200
Related Questions
A company's profit increased linearly from $5 million at the end of year 2 to $17 million at the end of year 6.
(a) Use the two (year, profit) data points (2, 5) and (6, 17) to find the linear relationship y = mx + b between x = year and y = profit.
(b) Find the company's profit at the end of 3 years.
(c) Predict the company's profit at the end of 8 years.
Answers
Below, you will learn how to solve the problem.
(a) To find the linear relationship y = mx + b between x = year and y = profit, we first need to find the slope (m) and the y-intercept (b).
The slope (m) is the change in y (profit) divided by the change in x (year):
m = (17 - 5)/(6 - 2)
m = 12/4
m = 3
Next, we can use one of the data points (2, 5) and the slope (3) to find the y-intercept (b):
5 = 3(2) + b
b = 5 - 6
b = -1
So the linear relationship between x = year and y = profit is:
y = 3x - 1
(b) To find the company's profit at the end of 3 years, we can plug in x = 3 into the equation:
y = 3(3) - 1
y = 8
So the company's profit at the end of 3 years is $8 million.
(c) To predict the company's profit at the end of 8 years, we can plug in x = 8 into the equation:
y = 3(8) - 1 = 23
So the company's profit at the end of 8 years is predicted to be $23 million.
For more information about equation, visit:
https://brainly.com/question/22688504
#SPJ11
a particular student often oversleeps and misses his alarm - this happens on 65% of school days. when he misses his alarm, the probability that he will be late to school is 0.75. when he doesn't miss his alarm, the probability that he will be late to school is 0.41. round all answers to 2 decimal places; make sure to type a 0 before the decimal place. a) if the student misses his alarm, what is the probability that he is not late to school? b) what is the probability that the student is late to school? c) one day, the student shows up to school on time. what is the probability that he missed his alarm?
Answers
a) If the student misses his alarm, the probability that he is not late to school is 0.25.
b) The probability that the student is late to school is 0.65.
c) One day, the student shows up to school on time. The probability that he missed his alarm is 0.59.
For A,
Let A be the event that the student wakes up on time, and B be the event that the student is late to school. We want to find P(B).
By definition,
P(B) = 1 - P(A)
where A is the event that the student misses his alarm.
Therefore,
P(B) = 1 - P(A)
= 1 -0.75
We are given that P(A') = 0.75, so
P(B) =0.25
For B,
To calculate the probability that the student is late to school, we will use the following formula:
P(X = x) = n!/(x!(n-x)!) * p^x * (1-p)^(n-x)
where:
P(X = x) is the probability that the student is late to school
n is the number of trials
x is the number of events
p is the probability of an event occurring
For this problem, we will let n = 1 and x = 1.
Now that we have our formula, we can plug in our values to solve for P(X = x).
P(X = x) = 1!/(1!(1-1)!) * 0.65^1 * (1-0.65)^(1-1)
P(X = x) = 0.65
We can interpret this answer as follows: there is a 0.65 probability that the student is late to school.
For C,
We first need to find the probability that the student did not miss his alarm, which is 1 - 0.59 = 0.41. We then need to find the probability that the student showed up to school on time given that he did not miss his alarm, which is 1 - 0.41 = 0.59.
Learn more about probability at : https://brainly.com/question/11234923
#SPJ4
find x
answer choices
6
7
9
10
8

Answers
The answer should be 10
Kaylin wants to make fudge to sell at break time at school.she finds the following recipe online:125grams of butter 420grams of castor sugar 1tin (397) of condensed milk 15ml vinegar. She finds the prices for the products at her local supermarket 500g butter R42,50 500g castor sugar R15,50 1tin condensed milk R24,95 750ml vinegar R15,25 100ml vanilla essence R19,95 if she buys 500g of butter ,how many times will she be able to make this recipe
Answers
She will be able to make the recipe approximately 4 times with 500g of butter. Each recipe requires 125g of butter, so dividing 500g by 125g gives a result of 4.
Since the recipe requires 125g of butter and she buys 500g, dividing the total amount of butter (500g) by the required amount per recipe (125g) gives the number of times she can make the recipe (4).
Sure! To calculate the number of times Kaylin can make the recipe with 500g of butter, we need to divide the total amount of butter she has by the amount of butter required per recipe.
The recipe calls for 125 grams of butter. If Kaylin buys 500 grams of butter, we divide 500 by 125: 500g / 125g = 4.
So, she will be able to make the recipe approximately 4 times with 500g of butter. Each time she makes the recipe, she will use 125g of butter, and since she has 500g in total, she can repeat the process 4 times.
Learn more about requires here:
https://brainly.com/question/4130932
#SPJ11
the perimeter of the polygon above 8cm 8cm 8 cm 8 cm all sides brainly

Answers
The polygon has 10 sides.
Each side of the polygon has a measure of 8 cm.
Therefore, the required perimeter is given by:
\(8\times10=80\)Therefore, the required perimeter is 80 cm
If f(x) = -3x + 1, find f(1) - 1
Answers
Answer:
f(1) - 1 = -3
Step-by-step explanation:
Step 1: Find f(1)
f(1) = -3(1) + 1
f(1) = -3 + 1
f(1) = -2
Step 2: Find f(1) - 1
f(1) - 1 = -2 - 1
f(1) - 1 = -3
Nick recently started a landscaping company. He began with 33 clients. Thanks to word-of-mouth referrals, his clients double each month. How many clients will Nick have after one year
Answers
After one year, Nick will have approximately 135,168 clients.
To calculate the number of clients Nick will have after one year, we need to determine the number of months in one year and apply the doubling rate each month.
There are 12 months in one year.
Starting with 33 clients, we can calculate the number of clients after each month:
Month 1: 33 clients * 2 = 66 clients
Month 2: 66 clients * 2 = 132 clients
Month 3: 132 clients * 2 = 264 clients
...
Month 12: (previous month's clients) * 2 = final number of clients after one year
We can continue this pattern until reaching Month 12:
Month 4: 264 clients * 2 = 528 clients
Month 5: 528 clients * 2 = 1056 clients
Month 6: 1056 clients * 2 = 2112 clients
Month 7: 2112 clients * 2 = 4224 clients
Month 8: 4224 clients * 2 = 8448 clients
Month 9: 8448 clients * 2 = 16896 clients
Month 10: 16896 clients * 2 = 33792 clients
Month 11: 33792 clients * 2 = 67584 clients
Month 12: 67584 clients * 2 = 135,168 clients
Therefore, after one year, Nick will have approximately 135,168 clients.
Learn more about Doubling Rate at
brainly.com/question/32659562
#SPJ4
Translate this sentence into an equation. A number b divided by three is equal to six less than c.
Please help
Answers
Answer:
B / 3 = 6 < 3
hope I helped.
what initial value might you consider with that slope? write a linear equation representing your example.
Answers
The initial value that I might consider with that slope is the y-intercept. The y-intercept is the point where the line crosses the y-axis, and it is the value of y when x is 0. So, if the slope is 2, then the y-intercept might be 1. This would give us the following linear equation:
y = 2x + 1
This equation represents a line that has a slope of 2 and a y-intercept of 1.
(-4m-2)+(2y+5.5m)+(5+6.7y) combine like terms. Pls help assap
Answers
(-4m-2)+(2y+5.5m)+(5+6.7y)
-4m + 5.5m = 1.5m
-2+5 = 3
2y+6.7y = 8.7y
Answer : 1.5m + 3 + 8.7y
A 12-ounce bottle of shampoo lasts Enrique for 9 weeks. How many weeks would you expect a 20-ounce bottle of shampoo to last him?
Answers
Answer:
15 weeks
Step-by-step explanation:
Find the quotient. Use a model to help you divide
6
.
15
÷
5
=
A.
1.03
B.
1.23
C.
1.3
D.
1.2
Answers
Answer:
Step-by-step explanation:
6.15/5=1.23
The answer is B.
Which of the following correctly uses exponents to write "6 factors of 2"? 2 6 6 ∙ 2 12 6 2
Answers
Answer:
C (6*2)
Step-by-step explanation:
Answer:
6 times 2
Step-by-step explanation:
Im not completely confident though so check other answers
Prove that f(x)=(2x+9)/(x+2) and f^-1(x)=(2x-9)/(2-x) are inverse functions by algebraically showing that f(f^-1(x))=f^-1(f(x))=x

Answers
The functions f(x) and f^-1(x) are inverse functions
How to prove the inverse functionsThe functions are given as
f(x) = (2x + 9)/(x + 2) and f^-1(x) = (2x - 9)/(2 - x)
To determine that they are inverse functions, we make use of the following:
showing that f(f^-1(x)) = x by substituting f^-1(x) into f(x) and simplifying the expression, andshowing that f^-1(f(x)) = x by substituting f(x) into f^-1(x) and simplifying the expression.using the above as a guide, we have the following:
f(f^-1(x)) = f((2x - 9)/(2 - x)) = (2((2x - 9)/(2 - x)) + 9)/(((2x - 9)/(2 - x)) + 2) = x
and
f^-1(f(x)) = f^-1((2x + 9)/(x + 2)) = (2((2x + 9)/(x + 2)) - 9)/(2 - (2x + 9)/(x + 2)) = x
Hence, f(x) and f^-1(x) are inverse functions.
Read more about inverse functions at
https://brainly.com/question/3831584
#SPJ1
Simplify. (√5-1)(√5+4)
Answers
Any mathematical statement that includes numbers, variables, and an arithmetic operation between them is known as an expression or algebraic expression. After simplifying the expression the answer is 4.
In the phrase \(4m + 5\), for instance, the terms 4m and 5 are separated from the variable m by the arithmetic sign +.
simplify the expression \((√5-1)(√5+4)\), you can use the difference of squares formula, which states that \((a-b)(a+b)\) is equal to \(a^2 - b^2.\)
In this case, a is \(√5\) and b is 1.
Applying the formula, we get \((√5)^2 - (1)^2\), which simplifies to 5 - 1. Therefore, the answer is 4.
Know more about expression here:
https://brainly.com/question/1859113
#SPJ11
Any mathematical statement that includes numbers, variables, and an arithmetic operation between them is known as an expression or algebraic expression. The simplified form of (√5-1)(√5+4) is 4.
To simplify the expression (√5-1)(√5+4), we can use the difference of squares formula, which states that \(a^2 - b^2\) can be factored as (a+b)(a-b).
First, let's simplify the expression inside the parentheses:
√5 - 1 can be written as (√5 - 1)(√5 + 1) because (√5 + 1) is the conjugate of (√5 - 1).
Now, let's apply the difference of squares formula:
\((√5 - 1)(√5 + 1) = (√5)^2 - (1)^2 = 5 - 1 = 4\)
Next, we can simplify the expression (√5 + 4):
There are no like terms to combine, so (√5 + 4) cannot be further simplified.
Therefore, the simplified form of (√5-1)(√5+4) is 4.
In conclusion, the expression (√5-1)(√5+4) simplifies to 4.
Learn more about expression :
brainly.com/question/1859113
#SPJ11
limit x as it approaches 1, ( 4x3 +3x2 +2x -2)
Answers
To evaluate the limit of the function f(x) = 4x^3 + 3x^2 + 2x - 2 as x approaches 1, we can substitute x = 1 into the function and calculate the resulting value.
When we substitute x = 1 into the function, we get f(1) = 4(1)^3 + 3(1)^2 + 2(1) - 2 = 4 + 3 + 2 - 2 = 7. This means that as x approaches 1, the function f(x) approaches the value of 7. In other words, the limit of f(x) as x approaches 1 is equal to 7.
Geometrically, we can interpret this result as follows. The function f(x) is a polynomial function of degree 3, which means that it is a cubic function. When we plot the graph of f(x), we get a curve that has a specific shape.
As x approaches 1 from both sides, we can see that the curve gets closer and closer to the horizontal line y = 7. This indicates that the limit of f(x) as x approaches 1 is indeed equal to 7.
Learn more about approaches here:
https://brainly.com/question/13443204
#SPJ11
3- Find all values of Z such that e² = 2+i√3
Answers
The values of Z such that e² = 2 + i√3 are Z = ln(2 + i√3) + 2πik, where k is an integer.
To find the values of Z, we can start by expressing 2 + i√3 in polar form. Let's denote it as re^(iθ), where r is the modulus and θ is the argument.
Given: 2 + i√3
To find r, we can use the modulus formula:
r = sqrt(a^2 + b^2)
= sqrt(2^2 + (√3)^2)
= sqrt(4 + 3)
= sqrt(7)
To find θ, we can use the argument formula:
θ = arctan(b/a)
= arctan(√3/2)
= π/3
So, we can express 2 + i√3 as sqrt(7)e^(iπ/3).
Now, we can find the values of Z by taking the natural logarithm (ln) of sqrt(7)e^(iπ/3) and adding 2πik, where k is an integer. This is due to the periodicity of the logarithmic function.
ln(sqrt(7)e^(iπ/3)) = ln(sqrt(7)) + i(π/3) + 2πik
Therefore, the values of Z are:
Z = ln(2 + i√3) + 2πik, where k is an integer.
The values of Z such that e² = 2 + i√3 are Z = ln(2 + i√3) + 2πik, where k is an integer.
To know more about polar form visit
https://brainly.com/question/30824428
#SPJ11
What is the answer to 10 =7-m
Answers
Answer:
\(m=-3\)
Step-by-step explanation:
\(10=7-m\\\\7-m=10\\\\7-7-m=10-7\\\\-m=3\\\\\frac{-m=3}{-1}\\\\ \boxed{m=-3}\)
Hope this helps.
In rectangle pqrs, pq = 18, ps = 14, and pr = 22.8. diagonals and intersect at point t. what is the length of ? a. 7 b. 9 c. 11.4 d. 22.8
Answers
In rectangle pqrs, pq = 18, ps = 14, and pr = 22.8. diagonals and intersect at point t. The length of diagonal from the intersection point p is correct option is c. 22.8
We have given rectangle PQRS
Side PQ =18 .
Side PS = 14 .
Diagonal PR = 22.8 .
Properties of rectangle :
Opposite sides of the rectangle are equals.
Diagonals of the rectangle are equal .
Diagonals of rectangles bisect each other.
Then by second property :
Diagonal PR =QS
QS = 22.8
By the Third property
TQ = 1/2× QS
TQ = 1/2 × 22.8
TQ = 11.4
A similar lengths problem is given at
https://brainly.com/question/17048953
#SPJ4
Answer:
Step-by-step explanation:
c. 11.4
provide the quantum numbers and related information for the following orbital, 3d. what is the maximum number of electrons in the entire shell?
Answers
The maximum number of electrons in the 3d orbital, which is 10.
The quantum numbers for the 3d orbital are:
- Principal quantum number (n) = 3
- Angular momentum quantum number (l) = 2 (d orbital)
- Magnetic quantum number (m) = -2, -1, 0, 1, 2 (five possible values for the d orbital)
- Spin quantum number (s) = -1/2, 1/2 (two possible values for electrons)
The maximum number of electrons in the entire 3d shell is 10. This is because the d orbital can hold a maximum of 5 pairs of electrons (2 electrons per pair), and there are 5 possible values for the magnetic quantum number (m) in the d orbital.
In general, the maximum number of electrons in an entire shell is given by the formula 2n^2, where n is the principal quantum number. For the 3d orbital, the principal quantum number is 3, so the maximum number of electrons in the entire shell is 2(3^2) = 18. However, the question specifically asks for the maximum number of electrons in the 3d orbital, which is 10.
Learn more about Quantum numbers
brainly.com/question/16977590
#SPJ11
A researcher asked 36 tourists which Caribbean island was their favourite The results showed that 9 tourists said Tobago. The researcher wants to draw a pie chart to show this information What should the angle for the Tobago segment measure?
A. 9 degree
B. 14 degree
C.25 degree
D. 90 degree
Answers
Explanation= the fraction would be 9/36 people think Tobago if that fraction were to made out of 360 degrees like in a circle it would be 90:360
.
32. A father tells his son, "I was of your present age when you were born," If the father is 36 now, how old was the boy 5 years back? (a) 13 (b) 15 (c) 17 (d) 20
Answers
Then, x - y = y or x = 2y,
Now, x = 36. So, 2y = 36 or y = 18.
Therefore Son's present age = 18 years.
So, son's age 5 years ago = 13 years.
It is now five past six. What time will it be in 11 hours and 32 minutes?
Answers
As part of a class project, Sarah and Geoffrey conducted a survey asking their peers whether they planned on taking a music class the next year.
of the 90 students they surveyed, 43 responded favorably. Sarah and Geoffrey calculated the margin of error for different confidence intervals.
Their work is shown.
Sarah
Geoffrey
95% confidence:
90% confidence
0.48(1 - 0.48
ME = 1.96 V
90
(8) 1 - 3
ME = 1.65V
133
Which student incorrectly found the margin of error and why?
O A Geoffrey incorrectly found the margin of error because he used the wrong critical value.
OB. Geoffrey incorrectly found the margin of error because he used the wrong sample size.
OC. Sarah incorrectly found the margin of error because she used the wrong sample proportion.
OD. Sarah incorrectly found the margin of error because she used the wrong critical value.

Answers
Answer:
Geoffrey incorrectly found the margin of error because he used the wrong sample size.
Please give me brainliest, I really need it.

x 0 1 2 3 4 p(x) 0.05 0.25 0.35 0.25 0.10 for the probability distribution above, what is the probability of an x that is at least 2?
Answers
The probability of an x that is at least 2 is 0.70.
The probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%.
P(E) means the probability of an event to occur.
P(E) is that of at least 2 means P(E) is greater than equals to 2, so we will take value greater than and equal to 2 i.e., 2,3,4
P(E) = P (X \(\geq\) 2)
= P(X=2) + P(X=3) + P(X=4)
= 0.35 + 0.25 + 0.10
= 0.70
Therefore, the required probability is 0.70.
To know more about probability
https://brainly.com/question/30034780
#SPJ4
(—5t^3+4t^2—t)—(8t^2+t)

Answers
Answer:
Step-by-step explanation:
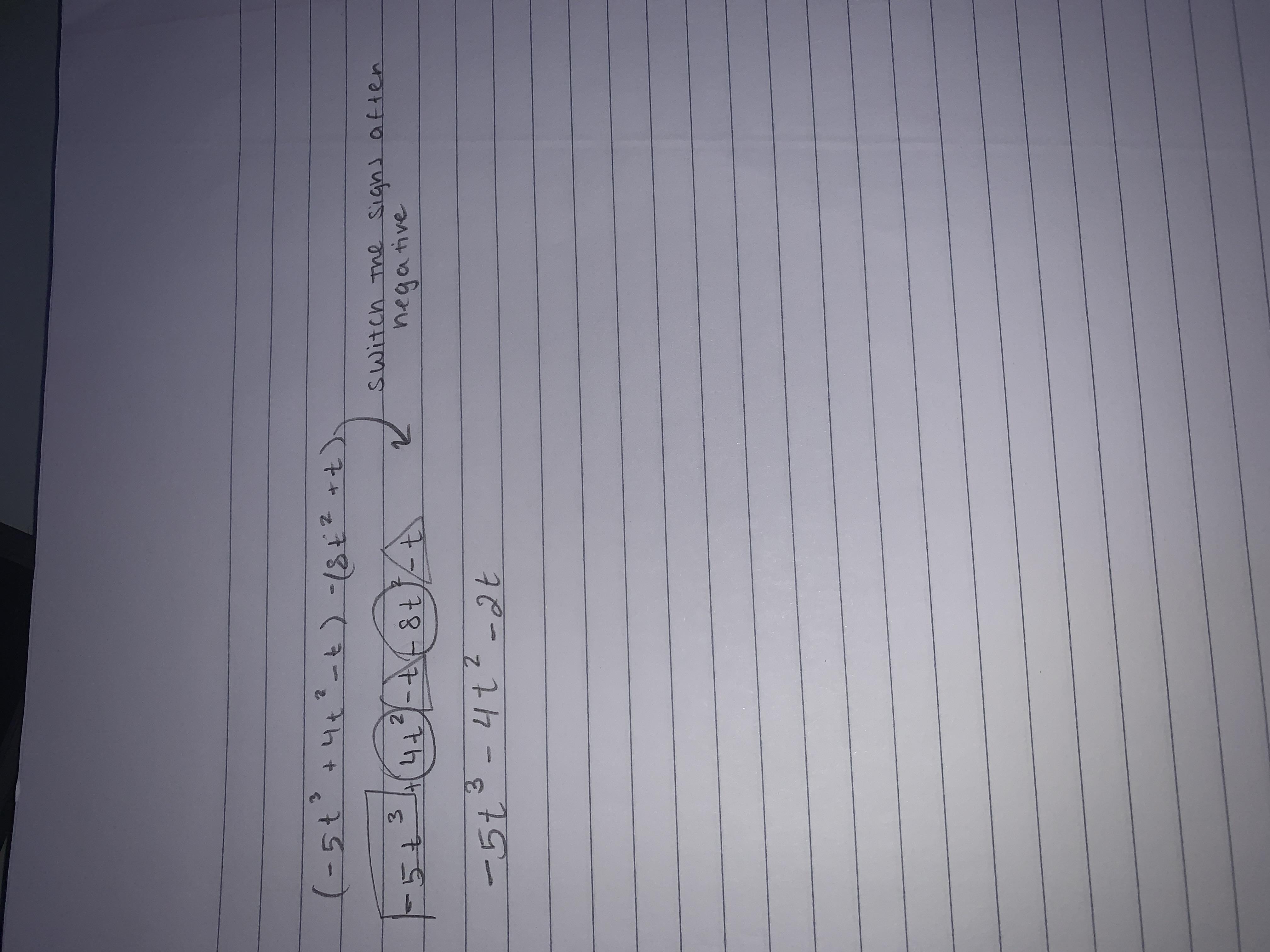
3b
Set up a triple integral that evaluates the volume below the plane \( 3 x+4 y+2 z=12 \). Then evaluate the integral.
Answers
The triple integral that evaluates the volume below the plane \(3x + 4y + 2z = 12\) is given by \(\iiint_V dV\), where \(V\) represents the region below the plane. The integral evaluates to a specific value based on the limits of integration.
To set up the triple integral, we need to determine the limits of integration for each variable. Since the region is defined by the plane \(3x + 4y + 2z = 12\), we can express \(z\) in terms of \(x\) and \(y\):
\[z = \frac{12 - 3x - 4y}{2}.\]
The limits for \(x\) and \(y\) can be determined by the intersection points of the plane with the coordinate axes. When \(x = 0\), we have \(y = 0\) and \(z = 6\). When \(y = 0\), we have \(x = 4\) and \(z = 6\). When \(z = 0\), we have \(3x + 4y = 12\), which yields \(x = 4\) and \(y = 3\).
Now we can set up the triple integral as follows:
\[\iiint_V dV = \int_{0}^{4} \int_{0}^{3} \int_{0}^{\frac{12 - 3x - 4y}{2}} dz\, dy\, dx.\]
To evaluate the triple integral \(\iiint_V dV\), we integrate with respect to \(z\), \(y\), and \(x\) using the limits determined earlier:
\[\int_{0}^{4} \int_{0}^{3} \int_{0}^{\frac{12 - 3x - 4y}{2}} dz\, dy\, dx.\]
First, we integrate with respect to \(z\):
\[\int_{0}^{4} \int_{0}^{3} \left[z\right]_{0}^{\frac{12 - 3x - 4y}{2}} dy\, dx.\]
Simplifying the expression, we get:
\[\int_{0}^{4} \int_{0}^{3} \frac{12 - 3x - 4y}{2} dy\, dx.\]
Next, we integrate with respect to \(y\):
\[\int_{0}^{4} \left[\frac{12y - 2xy - 2y^2}{2}\right]_{0}^{3} dx.\]
Simplifying further, we obtain:
\[\int_{0}^{4} (6 - 3x - 3x + 6) dx.\]
Now, integrating with respect to \(x\), we have:
\[\left[6x - \frac{3x^2}{2} + 6x\right]_{0}^{4}.\]
Evaluating this expression, we find:
\[\frac{72}{5}.\]
Therefore, the volume below the plane \(3x + 4y + 2z = 12\) is \(\frac{72}{5}\) cubic units.
To learn more about integral Click Here: brainly.com/question/31109342
#SPJ11
How do you find the slope and
y
-intercept of the line
−
7
x
−
9
y
=
27
?
Answers
The current, i, to the capacitor is given by i = -2e^(-2t)cos(t) Amps.
To find the current, we need to differentiate the charge function q with respect to time, t.
Given q = e^(2t)cos(t), we can use the product rule and chain rule to find the derivative.
Applying the product rule, we have:
dq/dt = d(e^(2t))/dt * cos(t) + e^(2t) * d(cos(t))/dt
Differentiating e^(2t) with respect to t gives:
d(e^(2t))/dt = 2e^(2t)
Differentiating cos(t) with respect to t gives:
d(cos(t))/dt = -sin(t)
Substituting these derivatives back into the equation, we have:
dq/dt = 2e^(2t) * cos(t) - e^(2t) * sin(t)
Simplifying further, we get:
dq/dt = -2e^(2t) * sin(t) + e^(2t) * cos(t)
Finally, rearranging the terms, we have:
i = -2e^(-2t) * sin(t) + e^(-2t) * cos(t)
Therefore, the current to the capacitor is given by i = -2e^(-2t) * sin(t) + e^(-2t) * cos(t) Amps.
Learn more about probability here
brainly.com/question/13604758
#SPJ11
A regular pentagon has an apothem measuring 20 cm and a perimeter of 145. 3 cm. A rectangular pentagon has an apothem measuring 20 centimeters and a perimeter of 145. 3 centimeters. What is the area of the pentagon? square centimeters.
Answers
The area of the pentagon is 1,453 squared centimeters.
Given information-
The length of the apothem of a regular pentagon is 20 cm.
The measure of the perimeter of a regular pentagon is 145.3 cm.
The length of the apothem of a rectangular pentagon is 20 cm.
The measure of the perimeter of a rectangular pentagon is 145.3 cm.
Pentagon-
Pentagon is the closed shaped polygon which has 5 sides. When these 5 sides are equal in length then the pentagon is called teh regular pentagon. When four of the sides of pentagon make a rectangle then the pentagon is called the rectangular pentagon.
Area of regular pentagon-Area of regular pentagon is half of the product of its apothem and perimeter. It can be given as,
\(A=\dfrac{1}{2} \times 20\times 145.3\\A=1453\)
Thus the area of the pentagon is 1,453 squared centimeters.
Learn more about the regular pentagon here;
https://brainly.com/question/858867
n one type of test before product launch, customers try a sample product and are then surveyed about whether they would buy/use the product again. this process is known asmultiple choicepremarket testing.alpha testing.prelaunch testing.concept testing.market testing.
Answers
Concept testing is the test done before product launch, clients try a sample product and are then surveyed about whether they would buy the product again. So, option D is correct.
In concept testing, the companies will give newly launched products or new ideas or prototype products to the potential customers, to take reactions from them. This feedback is collected and assisted and analyze the feedbacks in order to improve their products sale.
The main aim of this concept testing is to collect information, patron needs, and assertions and can take powerful good decisions. This can gauge the market price and sale of the products through advertising.
To learn more about Concept testing
https://brainly.com/question/3521552
#SPJ4
The complete question is:
type of test before product launch, customers try a sample product and are then surveyed about whether they would buy/use the product again. this process is known as:
a. premarket testing
b. alpha testing
c. prelaunch testing
d. concept testing
e. market testing.