what is the variable in the expression 3y+8
Answers
Answer:
y
Step-by-step explanation:
Variables are letters or symbols in an equation that represent a value we do not know.
In this equation, there is a y. y is not a number, but a letter, meaning this is the value we do not know, or the variable.
Answer:
y
Step-by-step explanation:
It is y because 8 will be constant and 3 will be a term I think and i know for y is variable
Related Questions
if you get right answer you get good review on here

Answers
(a) Use the Quotient Rule to differentiate the function f(x)=tan(x)-1/sec(x). f'(x)=
(b) Simplify the expression for f(x) by writing it in terms of sin(x) and cos(x), the find f'(x).
(c) Are your answers to part (a) and (b) equivalent?
For part (a) (which I got correct), I got f'(x)=-sin(x)tan(x)+sec(x)+sin(x)
I got part (b) wrong and I am certain it is a simple thing I am overlooking, but if someone could show me, I would appreciate it.
For part (c) I knew they were equivalent, and the answers is yes.
Answers
Answer:
(a) sin(x) + cos(x)
(b) sin(x) + cos(x)
(c) Both answers are equivalent
Step-by-step explanation:
(a) The given function is:
\(f(x) = \frac{tan(x)-1}{sec(x)}\)
According to the quotient rule:
\(f(x) = \frac{g(x)}{h(x)}\\f'(x)= \frac{g'(x)h(x)-g(x)h'(x)}{h(x)^2}\)
Applying the quotient rule:
\(f(x) = \frac{tan(x)-1}{sec(x)}\\f'(x)=\frac{sec^2(x)*sec(x)-(tan(x)-1)*sec(x)tan(x)}{sec(x)^2}\\f'(x)=\frac{sec^3(x)-sec(x)tan^2(x)+sec(x)tan(x)}{sec(x)^2}\\f'(x)=sec(x)+\frac{tan(x)-tan^2(x)}{sec(x)}\\ \frac{tan(x)}{sec(x)}=sin(x) \\f'(x)=sec(x)+sin(x)-sin(x)tan(x)\\\)
This can be simplified to:
\(f'(x)=sec(x)+sin(x)-sin(x)tan(x)\\f'(x) = \frac{1}{cos(x)}+sin(x)-\frac{sin^2(x)}{cos(x)}\\f'(x)=\frac{1+sin(x)cos(x)-sin^2(x)}{cos(x)}\\f'(x)=\frac{sin^2(x)+cos^2(x)+sin(x)cos(x)-sin^2(x)}{cos(x)}\\f'(x)=\frac{cos^2(x)+sin(x)cos(x)}{cos(x)}\\ f'(x)=sin(x) +cos(x)\)
(b) Simplifying in terms of sin(x) and cos(x):
\(f(x) = \frac{tan(x)-1}{sec(x)}\\f(x)=\frac{\frac{sin(x)}{cos(x)}-1 }{\frac{1}{cos(x)} } \\f(x)=sin(x)-cos(x)\\f'(x) = cos(x)+sin(x)\)
(c) As proven above, both answers are equivalent.
suppose section 1 has 30 students and section 2 has 20. find the sd of the scores of all the students in the class
Answers
The standard deviation of the scores of all the students in the class to be:
σ = √[(Σ(x - 80)2) / 50] = 11.18
The standard deviation of the scores of all the students in the class is calculated using the formula
σ = √[(Σ(x - μ)2) / N]
where μ is the mean of the scores and N is the total number of students in the class.
In this case, the total number of students in the class is 50 (30 from section 1 and 20 from section 2). Let's assume that the mean of the scores for all students is 80.
Therefore, the standard deviation of the scores of all the students in the class is calculated as follows:
σ = √[(Σ(x - 80)2) / 50]
In this equation, Σ(x - 80)2 is the sum of the squared differences between each student's score and the mean. We can calculate this sum by first finding the squared difference for each student and then adding them up.
For example, if the scores of the 30 students in section 1 are 86, 95, 78, etc., the squared differences will be (86 - 80)2 = 36, (95 - 80)2 = 225, (78 - 80)2 = 4, and so on. Adding all these squared differences will give us the sum of the squared differences for all the students in the class.
Finally, substituting this sum and the value of N (50) in the formula, we get the standard deviation of the scores of all the students in the class to be:
σ = √[(Σ(x - 80)2) / 50] = 11.18
Learn more about standard deviation here:
https://brainly.com/question/23907081
#SPJ4
Find the output, y, when the input, x, is -9.
y =

Answers
Answer:
when x=-9, y=1
Step-by-step explanation:
the graph shows when the x is at -9, the y is at 1

Please help on question asap if you are correct with answer I'll give brainlie st, a thanks and five stars.
When we have a trapezium and w e are finding out the area , would it be possible to have a radius\diameter in the trapezium or is that just for 3D shapes
Answers
Is not possible to define a radius nor a diameter in a trapezium.
Is it possible to have a radius/diameter in the trapezium?Radius and diameter are two measures defined for circles.
Radius is the distance between the center and any point in the circumference, and the diameter is the distance between two opposite points in the circumference (so it does not need to be 3D to have radius/diameter).
At the same time, a trapezium is not a circle, is a quadrilateral, so it can't have any of these.
To get the area use the formula:
Area = (base1 + base2)*height / 2
Learn more about trapeziums:
https://brainly.com/question/1410008
#SPJ1
The cost to rent a moving yan for a day is an initial cost of $29 plus $0.35 per mile driven, Find a function to model the cast of the moving van rental
based on the initial cost and miles driven
Answers
Hello!
miles driven = x
the initial cost = 29
f(x) = 29 + 0.35x
The length of a rectangle is 4 inches more than 4 times the width. The perimeter is 138 inches. Find the length and the width.
Answers
Find value of x in trapezoid

Answers
Answer:
x = 1
Step-by-step explanation:
You want to know the value of x in the trapezoid with adjacent angles (43x+2)° and 135°.
Supplementary anglesThe two marked angles can be considered "consecutive interior angles" where a transversal crosses parallel lines. As such, they are supplementary.
(43x +2)° +135° = 180°
43x = 43 . . . . . . . . . . . . . . divide by °, subtract 137
x = 1 . . . . . . . . . . . . . . . divide by 43
The value of x is 1.
__
Additional comment
Given that the figure is a trapezoid, we have to assume that the top and bottom horizontal lines are the parallel bases.
<95141404393>
Bernies cafe has regular coffee and decaffeinated coffee this morning the cafe served 80 coffees in all 48 of which were regular what percentage of the coffees were regular
Answers
We have to divide the number of regular ones by the total. Then multiply the result by 100.
48/80*100 = 60
Our answer is 60 % of the coffees were regular.
5. 5(x + 10) + x
A. 6x + 15
B.5x + 15
C.6x + 50
D.4x – 50
Answers
Answer: C
Step-by-step explanation:
first step is distributive prop. so times five by everything in parentheses
5x + 50 + x
then add common variables together
6x + 50
so your answer is C
(could you please mark this brainiest)
In September, 2,209 people visited the museum. In June, the number of visitors to the museum grew to 3,897.
Which of the following uses rounding to the nearest hundred to estimate the change in the number of visitors?
a) 4,000 – 2,000
b) 4,000 – 2,200
c) 3,900 – 2,200
d) 3,800 – 2,300
Answers
Answer:
3,900 – 2,200
Step-by-step explanation:
Given that,
In September, 2,209 people visited the museum.
In June, the number of visitors to the museum grew to 3,897.
2209 can be rounded off as 2200 to the nearest hundred place.
3,897 can be rounded off as 3900 to the nearest hundred place.
The required answer is :
3,900 – 2,200 = 1700
Hence, the correct option is (c).
How much would Carol have to invest today at 5.5% compounded annually to have $5300 for a vacation to China in three years?
Select one:
a.
$5023.70
b.
$4513.55
c.
$3179.08
d.
$4768.62
Answers
I Need Help Please This Will Only Take 1min…

Answers
The (C) solution of the equation is the value of the variable that causes an equation to be a true statement.
What are equations?A mathematical statement that has two expressions with equal values separated by the symbol "equal to" is called an equation. Consider the formula 3x + 5 = 15. Different types of equations exist, including linear, quadratic, cubic, and others.So, the Root or solution of the equation is the value of the variable that turns an equation into a true statement.
An equation that compares two mathematical expressions is a sentence or mathematical statement.The value of the variable that makes the equation true or satisfies it is referred to as the equation's root or solution.For instance,
"x + 2 = 0"The equation's solution in this case is x = - 2.
x² - 1 = 0Here, the equation's roots or solutions are x = 1 and -1.
Therefore, the (C) solution of the equation is the value of the variable that causes an equation to be a true statement.
Know more about equations here:
https://brainly.com/question/2972832
#SPJ13
The complete question is given below:
The value of the variable which makes an equation a true statement is called the ________ of the equation.
A. Coefficient
B. Equation
C. Solution
D. Algebraic expression
E. Constant
F. Variable

sphere edges vertices face ?
Answers
A sphere has no faces, no edges, and no vertices.
What are the faces, edges and vertices of a sphere ?A sphere is defined as the set of all points in three-dimensional space that are equidistant from a fixed point, called the center. The distance from the center to any point on the sphere is called the radius.
Spheres have a continuous, smooth, and curved surface, unlike polyhedra, which have flat faces, edges, and vertices. In contrast, a sphere does not have any flat faces, straight edges, or sharp corners. Its surface is entirely smooth and curved, with no distinct points where multiple edges meet.
Find out more on vertices at https://brainly.com/question/139603
#SPJ1
Use the number line below, where RS= 5y +5, ST = 4y + 8, and RT = 67.
a. What is the value of y?
b. Find RS and ST.
R
a. What is the value of y?
y = (Type an integer or a decimal.)
Answers
Answer:
y = 6RS = 35ST = 32Step-by-step explanation:
The segment sum theorem tells you the whole is the sum of the parts. That can be used to write an equation for y.
SetupRS +ST = RT
(5y +5) +(4y +8) = 67
SolutionSimplifying, we get ...
9y +13 = 67
9y = 54 . . . . . . . . subtract 13
y = 6 . . . . . . . . . divide by 9
RS = 5y +5 = 5·6 +5 = 35
ST = 4y +8 = 4·6 +8 = 32
The values of interest are ...
y = 6RS = 35ST = 321. Write down a pair of integers
(a) sum is -7
Answers
Answer:
-10, 3
Step-by-step explanation:
-10, 3 work since
-10 + 3 = -7
1) How many ink cartridges can you buy with 77 dollars if one cartridge costs 11 dollars ?
Answers
11x7=77
Please solve this with clear steps!!!!! 20 POINTS

Answers
The width of the river using the similar triangle is 43.3 metres.
How to find the width of the river?The surveyor wants to determine the width of the river . Let's use the pair of similar triangle to find the width of the river.
Therefore, two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion.
Hence, let's find the width of the river.
Therefore,
18.6 / 34.2 = AB / 79.6
cross multiply
18.6 × 79.6 = 34.2 AB
34.2 AB = 1480.56
divide both sides of the equation by 34.2
AB = 1480.56 / 34.2
AB = 43.2912280702
AB = 43.3 metres
learn more on similar triangle here: https://brainly.com/question/29191745
#SPJ1
4) Find the area of a
rectangular poster (in cm²)
that is 95 cm by 45 cm.
PLS HELPPPP
Answers
Answer:
I think it is 4275cm square.
Answer:
Area= 4275cm
Step-by-step explanation:
The area formula for a rectangle is length x width so if we plug in the numbers and multiply we get 4275 as our product.
Write as an algebraic expression and simplify if possible:
A number that is 20% greater than b
Answers
Answer:
1.2b
Step-by-step explanation:
When we say, "a number that is 20% greater than b," we're talking about a number that is ...
b + 20%×b
= b + 0.20b
= b(1 + 0.20)
= 1.2b
WILL GET BRAINLEST AND TONS OF POINTS
Answers
Answer:
Yamato's here!
Step-by-step explanation:
Oh well thank you! Have a nice and great holiday!!
(^ - ^ /)Xoxo, Yamato-
A slope field produces...
A. the graph of the general solution to the differential equation
B. the graph of the derivatives of the differential equation
Please explain. I am so confused on this.
Answers
It's A. B doesn't really make sense ("derivative of the differential equation" is somewhat nonsensical, "derivative of an equation" is not meaningful).
More to the point: Slope fields are used to visualize solutions to differential equations of the form
y' = f(x, y)
You take some point (x, y) and evaluate y' at the point. This gives the slope of the line tangent to the particular solution to the DE that passes through the point (x, y ).
Sample several points and evaluate y' at those points and you get several different slopes.
Simple example:
y' = x ² - y ² = (x + y ) (x - y )
Let's take the points (1, 1), (-1, 0), and (2, -2), at which we get slopes
y' = f (1, 1) = 0
y' = f (-1, 0) = 1
y' = f (2, -2) = 0
From here, you can get particular solutions that pass through a certain point by interpolating the slopes of the tangents to the solution. I've attached a slope field for the example here at the points listed above. (In the order red, green, black). Each light gray arrow in the background shows the slope of the tangent line.
If you're still unsure how the slope field is generated, I suggest looking up videos on the subject. The process is a bit difficult to describe without a dynamic visual aid.

How long will it take Kevin to complete all of his tasks?
Show your work.
Pls put in fraction form

Answers
Answer:
1/3 + 3/4 + 4/6 +1/2 =
Step-by-step explanation:
1/6 + 4/6 = 5/6
3/4 + 1/4 = 4/4
5/6 + 4/4 = 9/12
 Missed 10 days of Algebra 2. I think they did some Long Division stuff but i need help figuring out how to do this stuff...
I attached an image below of some example problems

Answers
"Find all real solutions of" basically means solve for x. You're looking for the real numbers x such that the given equation is satisfied. "Zeros" is synonymous with "solutions".
It looks like the first equation is
3x³ + x² - 38x + 24 = 0
It's not immediately obvious whether this can be factorized, so we first carry out the rational zero test to see if there are any rational solutions. *If* this equation has any rational solutions, then they must take the form of (divisor of 24)/(divisor of 3). That is, take any divisor of the constant coefficient and divide it by any divisor of the leading term's coefficient.
We have
• divisors of 24 : ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24
• divisors of 3 : ±1, ±3
Sadly, there are 64 possible roots to test, but we only need one to make the rest of the problem easier.
• Let x = +1 / +1 = 1. Then plugging x = 1 into the equation gives
3•1³ + 1² - 38•1 + 24 = -10 ≠ 0
so x = 1 is *not* a solution
• Let x = +2 / +1 = 2. If x = 2, then
3•2³ + 2² - 38•2 + 24 = -24 ≠ 0
so x = 2 is *not* a solution.
• Let x = +3 / +1 = 3. If x = 3, then
3•3³ + 3² - 38•3 + 24 = 0
so x = 3 is a solution.
By the remainder theorem, this means that x - 3 divides 3x³ + x² - 38x + 24. Using long or synthetic division,
(3x³ + x² - 38x + 24) / (x - 3) = 3x² + 10x - 8
so that
3x³ + x² - 38x + 24 = 0
is the same as
(x - 3) (3x² + 10x - 8) = 0
We factorize the remaining quadratic to get
3x² + 10x - 8 = (3x - 2) (x + 4)
and so the original equation is equivalent to
(x - 3) (3x - 2) (x + 4) = 0
Solve for x :
x - 3 = 0 or 3x - 2 = 0 or x + 4 = 0
x = 3 or x = 2/3 or x = -4
The other equations can be solved similarly, though some of the others you included are much simpler.
For the second problem (note that you left out an exponent), we solve the equation
x³ - 2x² - 23x + 60 = 0
Again, not immediately obvious how to factorize this. But using the rational root test, we have
• divisors of 60 : ±1, ±2, ±3, ±4, ±5, ±6, ±10, ±12, ±15, ±20, ±30, ±60
• divisors of 1 : ±1
If you follow the same steps as before, you'll find the first rational solution with x = 3. So x - 3 divides x³ - 2x² - 23x + 60, and long division gives
(x³ - 2x² - 23x + 60) / (x - 3) = x² + x - 20
and the resulting quadratic is easily factored,
x² + x - 20 = (x - 4) (x + 5)
So, we have
x³ - 2x² - 23x + 60 = (x - 3) (x - 4) (x + 5) = 0
which means
x - 3 = 0 or x - 4 = 0 or x + 5 = 0
x = 3 or x = 4 or x = -5
For the third problem, we can factor by grouping.
x³ - 4x² - x + 4 = 0
x² (x - 4) - (x - 4) = 0
(x² - 1) (x - 4) = 0
(x - 1) (x + 1) (x - 4) = 0
Then
x - 1 = 0 or x + 1 = 0 or x - 4 = 0
x = 1 or x = -1 or x = 4
For the fourth problem, we use the rational root test again, but twice this time.
x⁴ - 6x³ + 7x² + 6x - 8 = 0
• divisors of -8 : ±1, ±2, ±4, ±8
• divisors of 1 : ±1
We find that x = 1 and x = 2 are both rational roots, so both x - 1 and x - 2 divide x⁴ - 6x³ + 7x² + 6x - 8. By long division,
(x⁴ - 6x³ + 7x² + 6x - 8) / ((x - 1) (x - 2)) = x² - 3x - 4
and factoring this gives
x² - 3x - 4 = (x + 1) (x - 4)
So, we have
x⁴ - 6x³ + 7x² + 6x - 8 = (x - 1) (x - 2) (x + 1) (x - 4) = 0
which means
x - 1 = 0 or x - 2 = 0 or x + 1 = 0 or x - 4 = 0
x = 1 or x = 2 or x = -1 or x = 4
For the last problem,
x⁴ + 4x³ + 7x² + 16x + 12 = 0
we use the rational root test again.
• divisors of 12 : ±1, ±2, ±3, ±4, ±6, ±12
• divisors of 1 : ±1
We find that both x = -1 and x = -3 are rational solutions, and dividing gives
(x⁴ + 4x³ + 7x² + 16x + 12) / ((x + 1) (x + 3)) = x² + 4
which we cannot factorize further over the real numbers. So we end up with
x⁴ + 4x³ + 7x² + 16x + 12 = (x + 1) (x + 3) (x² + 4) = 0
so that
x + 1 = 0 or x + 3 = 0 or x² + 4 = 0
x = -1 or x = -3
(We omit the third equation here because it has no real solution since x² + 4 ≥ 4 for all real x.)
a builder has built 1/6 of the floors of a new skyscraper. If the builder has built 13 floors, how many floors will the skyscraper have when it is finished? Write and solve an equation to find the answer.
Answers
Answer: 78 floors total
Step-by-step explanation:
if 13=1/6
6 x 13=78
Answer:
13*6=78
Step-by-step explanation:
If one part of something is equal to 13, then 6 parts are equal to 13*6. Let us denote that "something" by x, and we get
\(x = 6 \times \frac{1}{6} x = 6 \times 13\)
Which is obviously an identity
ASAPP PLEAASSEE!!!
Nathan deposits $940 every 2 months into his daughter's RESP. If the account earns 3.99% / annual, compound quarterly, how much will be in the account after 25 years?
Answers
There will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
To calculate the amount in Nathan's daughter's RESP after 25 years, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = Final amount (amount in the account after 25 years)
P = Principal amount (amount deposited every 2 months)
r = Annual interest rate (in decimal form)
n = Number of times the interest is compounded per year
t = Number of years
In this case, Nathan deposits $940 every 2 months, so the principal amount (P) is $940. The annual interest rate (r) is 3.99% or 0.0399 in decimal form. Since the interest is compounded quarterly, the compounding frequency (n) is 4. The number of years (t) is 25.
Since Nathan deposits every 2 months, we need to calculate the total number of deposits made over 25 years. There are 12 months in a year, so in 25 years, there will be 25 * 12 = 300 months. However, since Nathan deposits every 2 months, the number of deposits (m) is 300 / 2 = 150.
Now, we can substitute these values into the formula:
A = 940(1 + 0.0399/4)^(4*25)
Calculating the exponent first:
(1 + 0.0399/4)^(4*25) ≈ 2.703236
Now, substituting the calculated exponent and the number of deposits into the formula:
A = 940 * 2.703236 * 150 ≈ $594,311.34
Therefore, there will be approximately $594,311.34 in Nathan's daughter's RESP after 25 years of depositing $940 every 2 months with a 3.99% annual interest rate compounded quarterly.
It's important to note that this calculation assumes Nathan makes the same $940 deposit every 2 months consistently over the 25-year period and does not make any withdrawals from the account during that time. Additionally, the actual amount may vary slightly due to rounding and any potential changes in interest rates over the years.
For more such questions on compounded visit:
https://brainly.com/question/24274034
#SPJ8
Which of the following numbers can be expressed as repeating decimals 4/7, 2/5, 7/8, 4/9. I will mark brainliest
Answers
Answer:
4/9
Step-by-step explanation:
Put it in a calculator and you get .4 but there's a lot of 4's. That's the repeating decimal.
Answer:4/9 and 4/7
Step-by-step explanation: Trust
What is the expression and value of “six less than nine times the sum of a number and eight” when n = 5? 9 (n + 8) minus 6; when n = 5, the value is 111. 6 minus 9 (n + 8); when n = 5, the value is 111. 9 (n) + 8 minus 6; when n = 5, the value is 47. 6 minus 9 (n) + 8; when n = 5, the value is 47.
Answers
Answer:
See below.
Step-by-step explanation:
9(n+8)-6
n=5
9(5+8)-6
9(13)-6
117-6
111
A sum is the answer to an addition expression or equation.
When one refers to "less than", they mean the number is "less than" the entirety of the expression or equation.
-hope it helps
evaluate -3 + (-4) * (-8)
Answers
Step-by-step explanation:
Was this answer helpful?
MARK ME AS A BRAINLIEST


I HOPE IT WILL HELP YOU.
Hope you have a great time.
Thanks
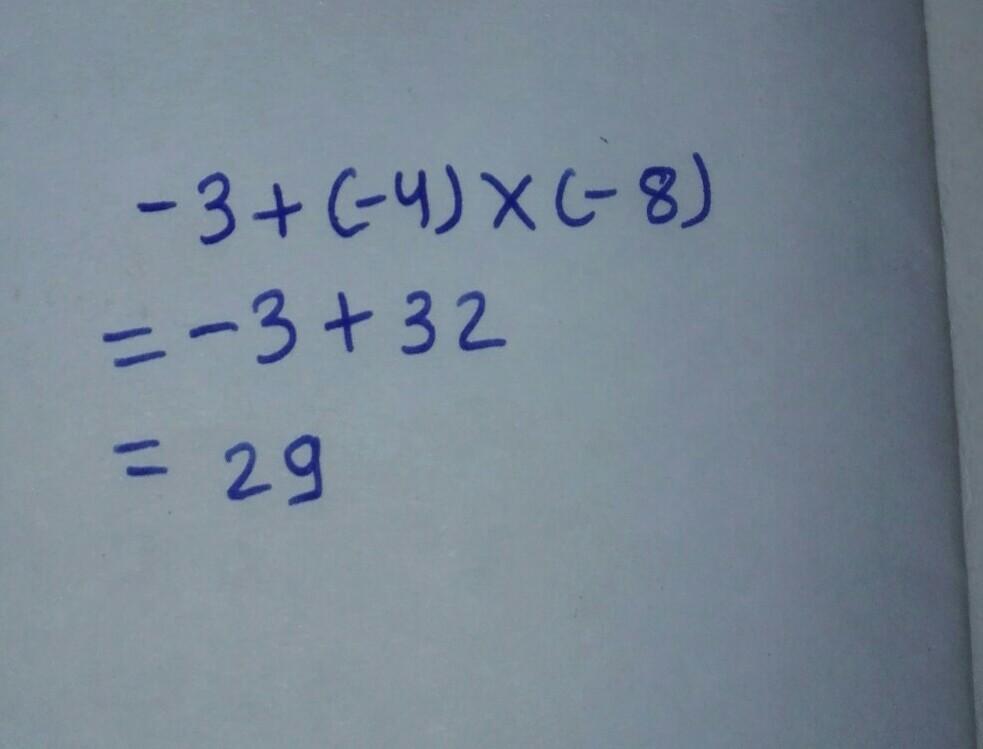
What is the solution to this inequality?
6x-5>-29
Ox>4
Ox>-4
Ox<-4
O x < 4

Answers
The solution to the given inequality would be \(x > -4\) (a.k.a. Option B)
Hope this helps!