what is one plus 59 plus 666662
Answers
Answer:
66,726
Step-by-step explanation:
Answer:
666,722
Step-by-step explanation:
1 + 59 + 666,662
= 60 + 666,662
= 666,722
i hope this helped
Related Questions
if the speed limt was 80 kilometers per hour, and elenas mom was driving 75 miles er hourm was sh speeding? by how much?
Answers
Answer: 40.7 kph is how much she was speeding
Step-by-step explanation:
You go shopping at the store
and find that 2 rolls of paper
towels cost $1.00, 3 rolls of
paper towels cost $1.50, and 4
rolls of paper towels cost
$2.00. It is proportional or not proportional
Answers
Answer:
yes it's proportional
Step-by-step explanation:
because you add 50 to every roll
What is 2/3 - 5 4/5
Answers
Answer:
The answer is 5 2/15.
Step-by-step explanation:
Well, you just do 4/5 - 2/3 then add 5 as the whole number.
The triangle below is a right triangle Find the length of the missing side provide in simplified radical form

Answers
Answer:
\(2\sqrt{10}\)
Step-by-step explanation:
Take \(a^{2} +b^{2} +c^{2}\), let x represent a, 9 represent b, and 11 represent c.
Now, plug your variables into the equation:
\(x^{2} +9^{2} =11^{2}\)
Simplify:
\(x^{2} +81=121\)
Subtract:
\(x^{2} =40\)
Take the square root of 40:
\(x=2\sqrt{10}\)
What is the measure of the unknown value
Y 77°
F measure

Answers
103 is y
here you go
If a pet grooming salon hires an additional groomer, that worker can groom 4 additional pets per day. the average grooming fee is $25. the most the salon would be willing to pay that groomer is
Answers
The most the salon would be willing to pay that groomer is $25×4 = $100.
What is unitary method?The unitary method is a technique that determines the worth of a single unit from value of multiple units, as well as the quality of multiple units from value of a single unit.
Some key features regarding the unitary method are-
It's a method which we use for the majority of math calculations. This method will come in handy when answering questions about ratio & proportion, algebra, geometry, and other subjects.We can determine the missing value using the unitary method. For example, if one carton of juice pays $5, how much would five such packets cost? We can then easily determine the price of 5 packets, which is $25.To know more about the unitary method, here
https://brainly.com/question/23423168
#SPJ4
18.8% converted to a decimal
Answers
Answer:
18.8% = 0.188 in decimal form. Percent means 'per 100'. So, 18.8% means 18.8 per 100 or simply 18.8/100. If you divide 18.8 by 100, you'll get 0.188 (a decimal number).
Step-by-step explanation:
Explanation: Just put a zero in front and a decimal before the 18.8
Find the values of a and b that make the following piecewise defined function both continuous and differentiable everywhere. f(x) = 3x + 4, X<-3
2x2 + ax + b. X>-3
Answers
The values of a and b that make the piecewise defined function f(x) = 3x + 4, for x < -3, and f(x) = 2x^2 + ax + b, for x > -3, both continuous and differentiable everywhere are a = 6 and b = 9.
To ensure that the piecewise defined function is continuous at the point where x = -3, we need the left-hand limit and right-hand limit to be equal. The left-hand limit is given by the expression 3x + 4 as x approaches -3, which evaluates to 3(-3) + 4 = -5.
On the right-hand side of the function, when x > -3, we have the expression 2x^2 + ax + b. To find the value of a, we need the derivative of this expression to be continuous at x = -3. Taking the derivative, we get 4x + a. Evaluating it at x = -3, we have 4(-3) + a = -12 + a. To make this expression continuous, a must be equal to 6.
Next, we find the value of b by considering the right-hand limit of the piecewise function as x approaches -3. Substituting x = -3 into the expression 2x^2 + ax + b, we get 2(-3)^2 + 6(-3) + b = 18 - 18 + b = b. To make the function continuous, b must equal 9.
Therefore, the values of a and b that make the piecewise defined function both continuous and differentiable everywhere are a = 6 and b = 9.
Learn more about piecewise
brainly.com/question/28225662
#SPJ11
PLEASE HELP DUE TODAY I'LL GIVE YOU 20 PTS AND POSSIBLY THE BRAINLIEST THING.
Which of the following demonstrates the Commutative Property of Multiplication?
5(2a − 3) = 10a − 15
10a − 15 = (2a − 3) ⋅ 5
5(2a − 3) = (2a − 3) ⋅ 5
(5 ⋅ 2a) − 3 = 5(2a − 3)
Answers
Answer:
C
Step-by-step explanation:
Because the Commutative Property means: Changing the order of factors does not change the product.
Therefore, the answer is C; 5(2a-3)=(2a-3)x5.
Hope this helps you!
Answer:
here you go so you mark that person the brainliest
Step-by-step explanation:
2,500 x 10
250,000/100
2,500/10
Which number is not equal to one of the following expressions
Answers
Answer:
b is not a part of that equation
pls answer this bc i need help with this

Answers
Answer:
A third degree or cubic polynomial with three terms. The constant term is -1/7, the leading term is -10x³ and the leading coefficient is -10
At presents a father's age is double his sons age. Five years ago,the product of their age was 1078 a) Find the Sons age at present b) fathers age at presents c)sons age five years ago
Answers
Based on the information, it is found that a) the son's age at present is 23, b) the father's age at present is 46, and c) the son's age five years ago was 18.
Let's first define the variables we will be using in this problem:
S = Son's age at present
F = Father's age at present
Now, we can write two equations based on the information provided in the question:
1) F = 2S (father's age is double the son's age at present)
2) (S - 5)(F - 5) = 1078 (the product of their ages five years ago was 1078)
We can substitute the first equation into the second equation to get:
(S - 5)(2S - 5) = 1078
2S2 - 15S - 1073 = 0
Using the quadratic formula, we can find the value of S:
S = (-(-15) ± √((-15)2 - 4(2)(-1073)) / (2(2))
S = (15 ± √10789) / 4
S = 23 or S = -23.25
Since age cannot be negative, we can conclude that the son's age at present is 23.
Now, we can use the first equation to find the father's age at present:
F = 2S
F = 2(23
F = 46
Finally, we can find the son's age five years ago by subtracting 5 from his current age:
S - 5 = 23 - 5 = 18
So, the son's age at present is 23, the father's age at present is 46, and the son's age five years ago was 18.
Here to learn more about the Quadratic Formula at the link https://brainly.com/question/8649555
#SPJ11
Given tan t = 2/3 and that pi <= t <= 3pi/2. Find exact value for each of the following:
a) sec t
b) cos t
c) sin t
d) csc t
e) cot t
Answers
well, first off let's notice something about angle "t", is between π and 3π/2, or namely the III Quadrant, where both "x" or adjacent side as well as "y" or opposite side are negative.
something else noteworthy is that, the hypotenuse is just a radius length and thus is never negative.
\(tan(t)=\cfrac{2}{3}\implies tan(t)=\cfrac{\stackrel{opposite}{-2}}{\underset{adjacent}{-3}}\qquad \textit{let's find the hypotenuse} \\\\\\ \textit{using the pythagorean theorem} \\\\ c^2=a^2+b^2\implies c =\sqrt{a^2+b^2} \qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ c=\sqrt{(-3)^2+(-2)^2}\implies c = \sqrt{9+4}\implies c = \sqrt{13}\)
\(\rule{34em}{0.25pt}\\\\ sec(t)=\cfrac{\stackrel{hypotenuse}{\sqrt{13}}}{\underset{adjacent}{-3}}~\hfill cos(t)=\cfrac{\stackrel{adjacent}{-3}}{\underset{hypotenuse}{\sqrt{13}}}\implies \cfrac{-3\cdot \sqrt{13}}{\sqrt{13}\cdot \sqrt{13}}\implies \cfrac{-3\sqrt{3}}{13}\)
\(sin(t)=\cfrac{\stackrel{opposite}{-2}}{\underset{hypotenuse}{\sqrt{13}}}\implies \cfrac{-2\cdot \sqrt{13}}{\sqrt{13}\cdot \sqrt{13}}\implies \cfrac{-2\sqrt{13}}{13} \\\\\\ csc(t)=\cfrac{\stackrel{hypotenuse}{\sqrt{13}}}{\underset{opposite}{-2}}~\hfill cot=\cfrac{\stackrel{adjacent}{-3}}{\underset{opposite}{-2}}\implies \cfrac{3}{2}\)
524800 in scientific notation?
Answers
Answer:
5.248 x 10^5
Step-by-step explanation:
there should be one digit and then however many decimals after. the exponent is positive because the original number is larger than one's digit.
it is assumed that a scuba diver will find it with probability 0.79, but it costs $ 700 to hire each diver. a)how many scuba divers should be hired in order to maximize the expected gain? answer: (round to nearest integer)
Answers
By using the probability we will find that we should hire 3 scuba divers to maximize the expected gain.
To find the number of scuba divers that should be hired to maximize the expected gain, we need to calculate the expected gain for each number of divers and choose the number with the highest expected gain.
Let X be the number of scuba divers hired, and let Y be the gain. Then the possible values of Y are $0 if the diver does not find the object, and $3000 if the diver finds the object. The probability of finding the object is 0.79, so the probability of not finding the object is 0.21.
The expected gain is then:
E(Y) = $3000 × 0.79 + $0 × 0.21 = $2370
The cost of hiring each diver is $700, so the net gain is:
Y - $700X
Therefore, the expected net gain is:
E(Y - $700X) = E(Y) - $700E(X)
= $2370 - $700X
To maximize the expected net gain, we take the derivative of this expression with respect to X and set it equal to zero:
d/dX (E(Y - $700X)) = - $700
Setting this equal to zero and solving for X gives:
$700X = $2370
X = 3.39
Rounding this to the nearest integer, we get 3.
Therefore, we should hire 3 scuba divers to maximize the expected gain.
To know more about Probability:
https://brainly.com/question/16722133
#SPJ4
A confectionery company mixes three types of toffees to form one kilogram " toffee packs. the pack is sold at rs. 17. the three types of toffees cost rs.20, rs. 10, rs. 5 per kg. resp. the mixture must contain atleast 300 gms of first type. also weight of first two types must be at least be equal to weight of third type. find the optimal mix for maximum profit.answer
Answers
The maximum profit is 6 and it is obtained when we mix 0.6 kg of type A, 0 kg of type B, and 0.4 kg of type C.
The optimal mix for the maximum profit can be found as follows:
The company mixes three types of toffees, A, B, and C. Let the weights of type A, B, and C be a, b, and c kg, respectively. Let us assume that we are making 1kg of toffee pack. Therefore, the weight of type C should be 1 - (a + b) kg. Also, the mixture must contain at least 300 gms of type A i.e a >= 0.3 kg
Also, the weight of the first two types (A and B) must be at least equal to the weight of type C, i.e a + b >= c. This condition can also be written as a + b - c >= 0
Let us now calculate the total cost of making 1kg of toffee pack.
Cost = 20a + 10b + 5c
If the pack is sold at Rs. 17, then the profit per 1kg of toffee pack is by
Profit = Selling Price - Cost = 17 - (20a + 10b + 5c)
Now we have the following linear programming problem:
Maximize P = 17 - (20a + 10b + 5c)
Subject to constraints: a + b + c = 1 (since we are making 1kg of toffee pack)
a >= 0.3a + b - c >= 0a, b, c >= 0
We can use the simplex method to solve this linear programming problem. However, to save time, we can solve it graphically. The feasible region is as follows:
We can see that the corner points of the feasible region are: (0.3, 0, 0.7), (0.6, 0, 0.4), (0, 0.5, 0.5), and (0, 1, 0).
Let us calculate the profit at each of these corner points. For example, at the point (0.3, 0, 0.7), we have a = 0.3, b = 0, and c = 0.7. Therefore, the profit is
P = 17 - (20(0.3) + 10(0) + 5(0.7)) = 3.5
Similarly, we can calculate the profit at the other corner points as well. The corner point (0.3, 0, 0.7) gives a profit of 3.5
Corner point (0.6, 0, 0.4) result in a profit of 6
Corner point (0, 0.5, 0.5) results in a profit of 5
Corner point (0, 1, 0) gives a profit of 3
You can learn more about optimal mix at: brainly.com/question/30629565
#SPJ11
Whenever he visits Belleville, Albert has to drive 6 miles due north from home. Whenever he visits Oxford, he has to drive 6 miles due east from home. How far apart are Belleville and Oxford, measured
Answers
The distance between Belleville and Oxford, measured is 6√13 miles.
To find the distance between Belleville and Oxford, we can use the Pythagorean theorem. We can imagine a right triangle with one leg measuring 6 miles (the distance Albert drives due north to reach Belleville) and the other leg measuring 6 miles (the distance Albert drives due east to reach Oxford).
Using the Pythagorean theorem, we can find the hypotenuse (the distance between Belleville and Oxford) by taking the square root of the sum of the squares of the other two sides:
√(6² + 6²) = √(36 + 36) = √72 = 6√2√2 = 6√4 = 6√(2²) = 6√4√2 = 6(2)√2 = 12√2
Therefore, the distance between Belleville and Oxford, measured is 6√13 miles.
Know more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
what is 600 hours in days?
Answers
Answer: 25 days
Step-by-step explanation:
Convert the unit for 600 hours
1 day = 24 hours
divide 600 hours with 24 hours as 24 hours = 1 day
600 ÷ 24 = 25
Is 3/2 the opposite of 6/4 on a number line? Please I’m so bad at this
Answers
Answer:
No, the opposite would be negative 6/4
Step-by-step explanation:
3/2 is just a simplified version of 6/4
Using the 68-95-99.7 Empirical Rule-of-Thumb, answer the following questions. No partial credit will be given for using any other method.
Students who had a low level of mathematical anxiety were taught using the traditional expository method. These students obtained a mean score of 450 with a standard deviation of 30 on a standardized test. The test scores follow a normal distribution.
a. What percentage of scores would you expect to be greater than 390? ( )%
b. What percentage of scores would you expect to be less than 480? ( )%
c. What percentage of scores would you expect to be between 420 and 540?( ) %
Answers
According to the 68-95-99.7 Empirical Rule-of-Thumb, we can make the following estimations for normally distributed data:
a. To find the percentage of scores greater than 390, we need to calculate the area under the normal curve to the right of 390. Since the mean is 450 and the standard deviation is 30, we can use the z-score formula:
z = (x - μ) / σ
where x is the value of interest, μ is the mean, and σ is the standard deviation. Plugging in the values, we have:
z = (390 - 450) / 30 = -2
Looking up the corresponding z-value in the z-table or using a calculator, we find that the area to the left of z = -2 is approximately 0.0228. Therefore, the percentage of scores expected to be greater than 390 is:
100% - 0.0228% = 97.72%
b. To find the percentage of scores less than 480, we use the same approach. Calculating the z-score:
z = (480 - 450) / 30 = 1
The area to the left of z = 1 is approximately 0.8413. Therefore, the percentage of scores expected to be less than 480 is:
0.8413 * 100% = 84.13%
c. To find the percentage of scores between 420 and 540, we calculate the z-scores for both values:
z1 = (420 - 450) / 30 = -1
z2 = (540 - 450) / 30 = 3
The area to the left of z = -1 is approximately 0.1587, and the area to the left of z = 3 is approximately 0.9987. Therefore, the percentage of scores expected to be between 420 and 540 is:
(0.9987 - 0.1587) * 100% = 84%
Please note that these calculations are based on the assumptions of a normal distribution and the 68-95-99.7 Empirical Rule-of-Thumb.
Learn more about arithmetic here
https://brainly.com/question/6561461
#SPJ11
I need help what’s the answers

Answers
Answer:
Quadratic
Step-by-step explanation:
The format for a quadratic function is: y= ax^2+bx+c.
This matches your equation.
An empty water tank is being filled at the rate of 20 liters per minute.
What will be the volume of water in the tank, in liters, after 11.5 minutes?
Please helppp :<
Answers
Answer:
230
Step-by-step explanation:
20x11=220
20x0.5=10
220+10=230
Your friends have locked themselves out of the house, and they need your help to get back in. They have a 20 foot long ladder, and there is an open window 16 feet above the ground. How far from the wall should you hold the base of the ladder while they climb back in?

Answers
Solution:
Given:
where;
\(\begin{gathered} l=20ft \\ h=16ft \end{gathered}\)A right triangle can be extracted from the image above,
Applying the Pythagoras theorem to the right triangle,
\(\begin{gathered} \text{hypotenuse}^2=\text{opposite}^2+\text{adjacent}^2 \\ \\ \text{Thus,} \\ l^2=h^2+w^2 \end{gathered}\)To find w, substitute the known values into the formula,
\(\begin{gathered} l^2=h^2+w^2 \\ 20^2=16^2+w^2 \\ 400=256+w^2 \\ 400-256=w^2 \\ 144=w^2 \\ w=\sqrt[]{144} \\ w=\pm12 \\ Si\text{nce the problem is on the distance to hold the base of the ladder, we pick the positive value only.} \\ \text{Thus,} \\ w=12ft \end{gathered}\)Therefore, the distance from the wall that the base of the ladder should be while they climb back in is 12 feet.
Hence, option D is the correct answer.


Dwayne buys 1 loaf of bread and 6 eggs for $4.45. Sheila buys 1 loaf of bread and 1 dozen eggs for $5.65. Let x be the cost, in dollars, of a loaf of bread. Let y be the cost, in dollars, of an egg.
Answers
Answer:
cost of bread = $3.25
Cost per egg = $0.2
Step-by-step explanation:
Given the following :
Cost of a loaf of bread and 6 eggs = $4.45 - - (1)
Cost of a loaf of bread and a dozen eggs ( 12 eggs) = $5.65 - - - (2)
Let x = cost of bread and y = cost of egg
x + 6y = 4.45
x + 12y = 5.65
Subtract 1 from 2
6y - 12y = 4.45 - 5.65
-6y = - 1.2
y = $0.2
Hence,
From x + 6y = $4.45
Where y = $0.2
x + 6($0.2) = $4.45
x + $1.2 = $4.45
x = $4.45 - $1.2
x = $3. 25
Hence, cost of bread = $3.25
Cost per egg = $0.2
pleeeeeeeeeeaaaaaassssseeee help
Answers
Answer:
with wut
Step-by-step explanation:
A rectangular book measures 4 x 7. What is the length of its
diagonal?
Answers
A rectangular book measures 4 x 7, the length of its diagonal is √65.
Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
In mathematical terms, if a and b represent the lengths of the two shorter sides (also known as legs) of a right triangle, and c represents the length of the hypotenuse, then the Pythagorean theorem can be expressed as:
a² + b² = c²
Given:
Base = 4
Length = 7.
To determine the length of diagonal by using Pythagorean theorem.
Diagonal² = Base² + Length²
Plugging the values in Pythagorean theorem.
Diagonal² = 4² + 7²
Diagonal = √(16 + 49) =√65.
Therefore, the length of diagonal of book is √65.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ2
helllllpppppppppp idk what it issssss
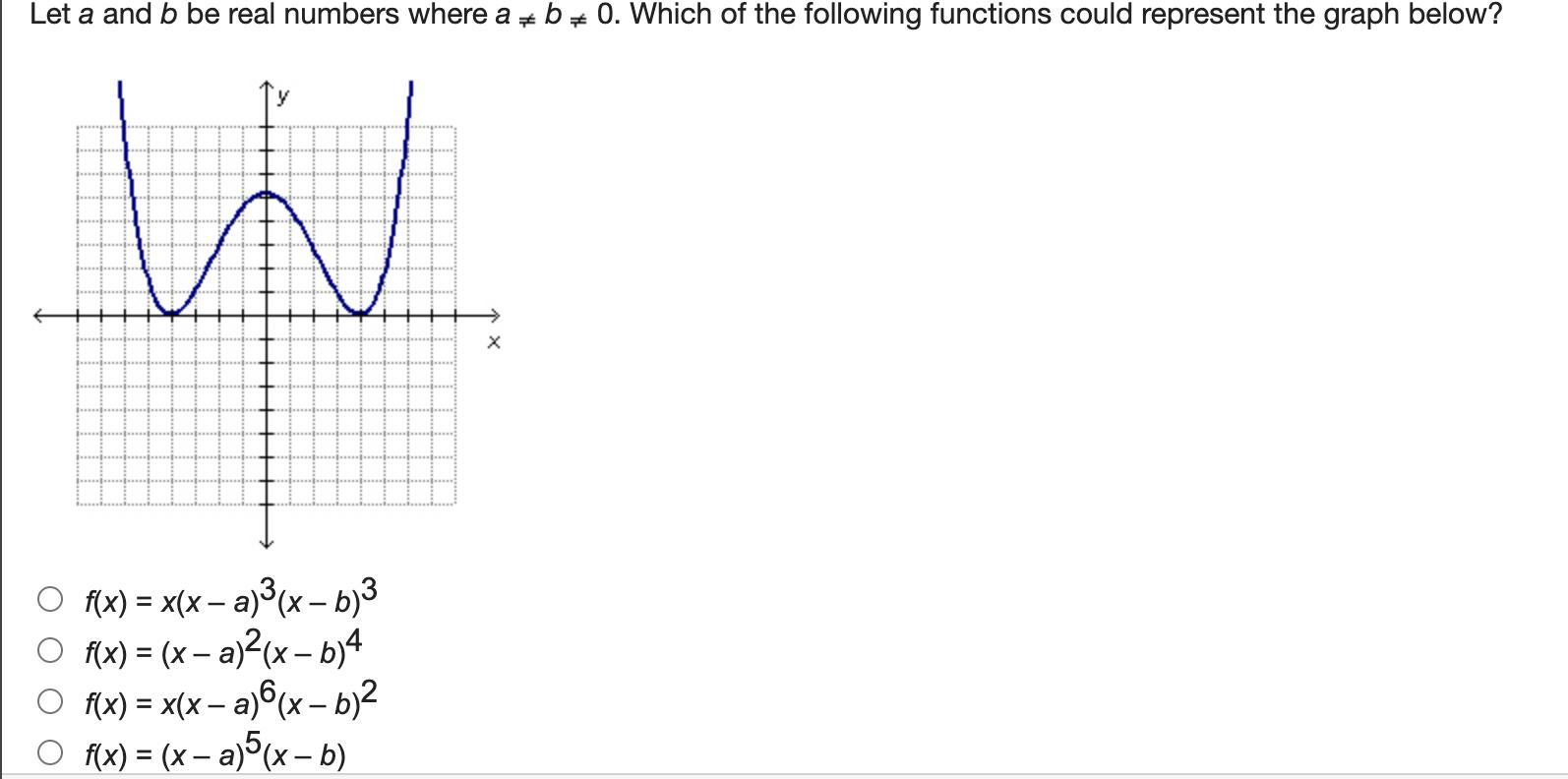
Answers
You need to compute the 99% confidence interval for the population mean. How large a sample should you draw to ensure that the sample mean does not deviate from the population mean by more than 1.3
Answers
To compute the 99% confidence interval for the population mean, you need to determine the appropriate sample size to ensure that the sample mean does not deviate from the population mean by more than 1.3. The key terms involved in this process are the confidence interval, sample size, population mean, and sample mean.
The confidence interval represents the range within which the population parameter (in this case, the population mean) is likely to fall, given a certain level of confidence. A 99% confidence interval means that you are 99% confident that the true population mean falls within the specified range.
To calculate the required sample size, you will need to use the formula for the margin of error (E), which is E = (Zα/2 * σ) / √n, where Zα/2 is the critical value associated with the desired level of confidence (99%), σ is the population standard deviation, and n is the sample size.
Since you want the sample mean to not deviate from the population mean by more than 1.3, you will need to set E = 1.3 and solve for n. After finding the critical value for a 99% confidence interval (which is approximately 2.576) and assuming you know the population standard deviation, you can plug these values into the formula and solve for n.
By doing this, you will be able to determine the appropriate sample size to ensure that the 99% confidence interval for the population mean is within 1.3 units of the sample mean.
To learn more about confidence interval click here
brainly.com/question/22851322
#SPJ11
Evaluate the expression:
3(a + b - 3) - 2(2a + b - 4) when a = -1 and b = 1
Answers
Answer:
1
Step-by-step explanation:
3x-2y=7
-x+3y=-7
What is the simultaneous answer?
Answers
Answer:
x = 5, Y = 4
Step-by-step explanation:
3x -2y = 7
-3x +9y = 21. (multiple the whole thing by 3 to get the xs to cancel)
7y = 28
y = 4
substitute y to find x
3x - 2(4) = 7
3x -8 = 7
3x = 15
x = 5