Use the properties of geometric series to find the sum of the series. For what values of the variable does the series converge to this sum?.
Answers
The given series diverges for all values of the variable since the absolute value of the common ratio (3/2) is greater than 1.
The sum of a finite geometric series is given by the formula:S=ar(r^n -1)/(r -1)where S is the sum, a is the first term, r is the common ratio and n is the number of terms. If we take the limit of this formula as n approaches infinity and as r is between -1 and 1 (inclusive), then we have the sum of an infinite geometric series:S=a/(1-r)The sum of the given infinite series will converge if and only if the absolute value of the common ratio is less than 1. Therefore, to find the values of the variable for which the series converges, we must find the absolute value of the common ratio and ensure that it is less than 1.Sum of series:S = 1 + 3/2 + 9/4 + ...+ [3^(n-1)]/[2^(n-2)] + ...The first term is a = 1.The common ratio is r = 3/2.Therefore, we can write:S = 1 + 3/2 + 9/4 + ...+ [3^(n-1)]/[2^(n-2)] + ...= a/(1-r) = 1/[1 - (3/2)] = 1/(1/2) = 2.For what values of the variable does the series converge to this sum?As the common ratio is 3/2 and the absolute value of this ratio is greater than 1, the given series diverges for all values of the variable.
learn more about the variable here;
https://brainly.com/question/31397680?
#SPJ11
Related Questions
Worksheet 1.3
Part 1: Write a math expression for each problem (model the problem).
1)
Lumpy drove for h hours at 50 mph. How far did he drive?
Answers
Answer:
50h milesStep-by-step explanation:
For us to write a math expression for the problem, we will use the formula for calculating speed.
Speed is the change of distance of a body with respect to time.
Mathematically, Speed = Distance/Time
Distance = Speed * Time
If Lumpy drove for h hours at 50 mph, then Lumpy speed = 50mph and time = h hours.
Substituting the given parameters into the formula to get the distance;
Distance = 50mph * h hours
Distance = 50h miles
Hence the math expression that modeled how far Lumpy drive is 50h miles
Lucy is deciding between two final options, both located at their respective centroids. In Option 1, Lucy works at the coffee shop and lives in Apartment E. In Option 2, Lucy works at the restaurant and lives in Apartment F. Which would you recommend? Justify your answer with a mathematical explanation
Answers
I would recommend Option 1, where Lucy works at the coffee shop and lives in Apartment E. This recommendation is based on a mathematical explanation involving the concept of centroids.
To make the recommendation, we need to consider the centroids of the two options. The centroid is the geometric center of a shape, which can be calculated using the average of the coordinates of its vertices. In this case, the centroids represent the average location of Lucy's work and residence.
Assuming Lucy's work and residence locations are represented as points in a two-dimensional coordinate system, we can calculate the centroid for each option. Let's denote the coordinates of the coffee shop as (x1, y1), the apartment E as (x2, y2), the restaurant as (x3, y3), and the apartment F as (x4, y4).
By calculating the average of the x-coordinates and y-coordinates separately, we obtain the centroid for Option 1 as (x1 + x2)/2, (y1 + y2)/2, and the centroid for Option 2 as (x3 + x4)/2, (y3 + y4)/2.
Now, to determine which option is closer to Lucy's average location, we need to calculate the distance between Lucy's average location and the centroids of each option. We can use the distance formula, which calculates the Euclidean distance between two points in a two-dimensional space.
By comparing the distances, if Option 1 has a smaller distance to Lucy's average location than Option 2, it means that Option 1 is closer to the average, and hence it is recommended. Conversely, if Option 2 has a smaller distance, it would be the recommended choice.
In summary, by calculating the centroids of both options and comparing the distances to Lucy's average location, we can determine which option is closer. Based on this mathematical analysis, I would recommend Option 1, where Lucy works at the coffee shop and lives in Apartment E.
Learn more about centroids here:
https://brainly.com/question/21361838
#SPJ11
The temperature at noon is 75 degrees. The temperature drops 3 degrees every half hour. What is the temperature at 4 p.m.
Answers
Answer:51 degrees
Step-by-step explanation:
At noon the temperature is 75 degrees
the temperature drops 3 degrees every half hour.
First solve for time elapsed between noon and 4, which is 4 hours.
Next, we can change our rate to be in terms of full hours instead of half hours using the fact that 1 hr = 2 half hours, so the temperature drops 6 degrees every hour.
Four hours have elapsed so multiply 6*4 = 24 degrees and then subtract it from the starting 75
75 - 24 = 51.
Verify that the intermediate value theorem applies to the indicated interval and find the value of c guaranteed by the theorem. f(x) = x2 4x 2, [0, 9], f(c) = 23 c =
Answers
The intermediate value theorem applies to the indicated interval and the importance of c guaranteed by the theorem is c=2,3.
Especially, he has been credited with proving the following five theorems: a circle is bisected via any diameter; the bottom angles of an isosceles triangle are the same; the other (“vertical”) angles are shaped by means of the intersection of two traces are same; two triangles are congruent (of identical form and size.
In mathematics, a theorem is an announcement that has been proved or may be proved. The evidence of a theorem is a logical argument that makes use of the inference guidelines of a deductive system to set up that the concept is a logical result of the axioms and formerly proved theorems.
In line with the Oxford dictionary, the definition of the concept is ''a rule or principle, especially in arithmetic, that may be proved to be true''. For example, in arithmetic, the Pythagorean theorem is a theorem and is maximum extensively used in the domain of science.
2-1and interval = [4]
since function text is continuous in a given interval. And also
+(4) = 42+4 = 4-1
20 = 6667
$(5/4) = ($145/2
stone-1
= 5.833
simple, f(4) > $(5/2), hence Intermediate
Theorem & applies to the indicated proved.
Now,
= 6 C-1
C-5c +6 = 0
C=2 or c=3
1=3 or
C= 2, 3
<= 2
Learn more about theorem here https://brainly.com/question/26594685
#SPJ4
Need help w this problem

Answers
Answer:
9, 18Step-by-step explanation:
The key word "product" tells us to multiply.
And, you probably know, but "integer" just means "number".
The question is, essentially:
A × B = 162 where A is half of B.
As someone who was never gifted in math, my best suggestion for something like this is to grab a calculator and start dividing 162 by all the numbers below 10. You will know you've got your answer when the calculator gives you a number that is twice the number you divided by.
In this case, I divided 162 by 9 and got 18. Since 9 is half of 18, and multiplied they make 162, we know this is the correct answer.
Hope this helps
Rod waxes two thirds of his car with one fourth bottle of car wax. What fraction of the bottle of car wax will Rod need to wax his entire car?
Answers
Step by step
Use x for car wax
2/3x = 1/4 × 1 car
2/3x = 1/4
Divide both sides by 2/3 to solve for x
x = 1/4 divided by 2/3
Note to divide fractions flip the 2/3 and multiply
x = 1/4 × 3/2 multiply across
x = 3/8.
Machlab Equipment is comparing three machines to determine which one to purchase. Each machine has a unique price, annual operating cost, and life span. Which one of the following computational methods should Machlab use as the basis for its decision? Multiple Choice Internal rate of return Net present value Equivalent annual cost Depreciation tax shield Bottom-up operating cash flow
Answers
Machlab Equipment should use the Net Present Value (NPV) as the computational method to make its decision.
The Net Present Value (NPV) is a widely used computational method for investment decisions. It takes into account the initial investment cost, annual operating costs, and expected cash flows over the life span of the machines. By discounting these cash flows to their present value, the NPV determines the profitability and economic viability of each machine.
To compare the three machines, Machlab Equipment can calculate the NPV for each interest by subtracting the initial investment cost from the present value of the expected cash inflows. The Equivalent Annual Cost (EAC) and Bottom-up Operating Cash Flow methods may provide useful information but may not capture the overall profitability and financial impact of the investment.
Learn more about interest here:
https://brainly.com/question/30955042
#SPJ11
2 [2 (3 – 52) + 4] = 5 [2 (3 – 3x) + 2]
Algerbra 1, solve for x.
Answers
Answer:
×=-90
Step-by-step explanation:
Given:2×+4=3×-2
3 5
write a polynomial function in standard form with the given zeros x=1,-1,-2
Answers
Answer:
y = x³ +2x² -x -2
Step-by-step explanation:
A polynomial with root q has a factor (x -q). The factored form of the polynomial is ...
y = (x -1)(x +1)(x +2)
y = (x² -1)(x +2) . . . . . . partial simplification
y = x³ +2x² -x -2
A political scientist surveys 28 of the current 157 representatives in a state's legislature. What is the size of the sample: What is the size of the population
Answers
In a political study, 28 out of 157 current representatives of a state's legislature are surveyed. The sample size is 28 and the population size is 157.
Sample size and population size are two important elements of statistics.
In a survey, a sample refers to a subset of people or items from a larger population.
Researchers select samples because it's impossible to conduct a study on the whole population due to time, cost, and other factors.
A sample is considered representative of the population if it is chosen randomly and if the sample size is large enough.
The population is the entire collection of people, items, or data that the researcher wants to analyze.
In the study, it is the total number of current representatives in the state's legislature.
Sometimes it is challenging to access the population. The sample is then obtained from the population.
The sample size and population size are two important elements of statistics.
Sample size is the number of individuals in a study, while the population size is the total number of individuals who could be studied.
To know more about size visit:
https://brainly.com/question/31259901
#SPJ11
Chapter 5 Lesson 1 Adding and Subtracting Polynomials

Answers
Polynomial \(-4x^2y\) is called a monomial of degree 3 and a polynomial \(3x^4 - 2x^3 - 5x^2 + 6x - 12\) is a quintic polynomial.
What is a pοlynοmial?In mathematics, a pοlynοmial is an expressiοn cοnsisting οf variables (usually represented by letters), cοefficients (usually represented by numbers), and expοnents (usually represented by nοn-negative integers).
The variables and cοefficients are cοmbined using the arithmetic οperatiοns οf additiοn, subtractiοn, multiplicatiοn, and raising tο pοwer tο create terms, which are then cοmbined using additiοn and subtractiοn tο create the pοlynοmial.
1) The polynomial \(-4x^2y\) has a degree of 3 and a single term, so it is called a monomial of degree 3.
2) The polynomial \(3x^4 - 2x^3 - 5x^2 + 6x - 12\) has a degree of 4 and five terms, so it is called a polynomial of degree 4 and five terms, or simply a quintic polynomial.
3) The polynomial \(x^2 + 5x - 4\) has a degree of 2 and three terms, so it is called a polynomial of degree 2 and three terms, or simply a quadratic polynomial.
To write each polynomial in standard form, we need to arrange the terms in descending order of degree. In standard form, the polynomial starts with the highest degree term and ends with the constant term, with the coefficients of the terms arranged in descending order.
4) \(x^3 + 3x^2 - 5x - 4\)
5) \(-x^5 + 4x^4 + 2x^3 + 2x - 7\)
6) \(-x^2 + 5x + 9\)
To combine like terms and write each expression in standard form, we need to simplify the coefficients of each variable to obtain the sum of the like terms:
7) \(-5y + 3y^2 + 2y - 2y^2 - 9\)
=\((3y^2 - 2y^2) + (-5y + 2y) - 9\)
=\(y^2 - 3y - 9\)
8) \(-2x^2 + x + 5x^3 + 4x + 2x^2\)
= \(5x^3 + 3x\)
9) \(x^2 - 5 + 2x + x^2\)
= \(2x^2 + 2x - 5\)
To know more about polynomials visit:
brainly.com/question/29135551
#SPJ1
(a) How many minutes are there between 8.50 pm and 10.05 pm?
5.
Answers
Answer:
75 minutes
Step-by-step explanation:
hope this helps
From her home, Jada would have to walk 3 miles north to get to her friend Brianna's house and 4 miles east to get to her friend Luke's house. One day, Jada walked from her home to Luke's house. Together, Luke and Jada cut directly through the field that separated them from Brianna's house. When they finished playing at Brianna's, Jada walked back home. In all, how far did Jada walk?
Answers
Answer: 12 miles
Step-by-step explanation: Stright from her house to luke is 5 miles back ti brianna is 4 miles and back home is 3 miles all together 5+4+3=12
find the product of
Answers
=1/5
Please mark brainliest
A store has a goal to increase monthly sales by 20%. If they sold 50 sweaters last month, how many sweaters do they need to sell this month to meet their goal?
Answers
Answer:
they need to sell 60 sweaters
10 more than 50
Step-by-step explanation:
20% of 100 is 20
20% of 50 is 10
20 divided by 2 equals 10
Find an equation of the tangent line to the curve at the given point. y = x^3 ? 3x + 2, (4, 54) Please show work
Answers
The slope of the tangent line at (4, 54) is 45. So the equation of the tangent line to the curve y = x^3 - 3x + 2 at the point (4, 54) is y = 45x - 126.
To find the equation of the tangent line to the curve y = x^3 - 3x + 2 at the point (4, 54), we need to use calculus. First, we find the derivative of the function:
y' = 3x^2 - 3
Next, we plug in x = 4 to find the slope of the tangent line at that point:
y'(4) = 3(4)^2 - 3 = 45
So the slope of the tangent line at (4, 54) is 45. To find the equation of the line, we use the point-slope form of the equation:
y - y1 = m(x - x1)
where m is the slope and (x1, y1) is the point on the line. Plugging in our values, we get:
y - 54 = 45(x - 4)
Simplifying, we get:
y - 54 = 45x - 180
y = 45x - 126
So the equation of the tangent line to the curve y = x^3 - 3x + 2 at the point (4, 54) is y = 45x - 126.
To find the equation of the tangent line to the curve y = x^3 - 3x + 2 at the point (4, 54), we need to first find the derivative of the function and then use the point-slope form of a line.
1. Find the derivative of the function with respect to x:
y'(x) = d/dx (x^3 - 3x + 2) = 3x^2 - 3
2. Evaluate the derivative at the given point (4, 54) to find the slope of the tangent line:
m = y'(4) = 3(4)^2 - 3 = 3(16) - 3 = 48
3. Use the point-slope form of a line (y - y1 = m(x - x1)):
y - 54 = 48(x - 4)
4. Simplify the equation:
y - 54 = 48x - 192
y = 48x - 138
So, the equation of the tangent line to the curve y = x^3 - 3x + 2 at the point (4, 54) is y = 48x - 138.
Visit here to learn more about derivative : https://brainly.com/question/25324584
#SPJ11
Find the missing angle.

Answers
Answer:
45 Degrees
Step-by-step explanation:
This would be a right angle. The other side would be 45 Degrees. Which when you add them equals 90.
Answer:
45 degrees
Step-by-step explanation:
The following figure shown is a square
All of the angles in a square are right angles meaning that they equal 90
If a diagonal line cuts through the middle then it splits the right angle into to 45 degree angles therefore your answer is 45 degrees
A poll conducted by the UC Berkeley Institute of Governmental studies in 2019 found that 51.7% of 4527 respondents said they considered moving out of the state.Here n=4527 and p^=51.7=0.517 , andq^=1-p^=1-0.517=0.483Now to compute 95% confidence interval for the proportion of all California who considered moving out of state.
Answers
The 95% confidence interval for the proportion of all Californians who considered moving out of state is (0.504, 0.530). We can be 95% confident that the true proportion of all Californians who considered moving out of state lies between 50.4% and 53.0%.
The UC Berkeley Institute of Governmental Studies conducted a poll in 2019 with 4,527 respondents in California, where 51.7% of them reported considering moving out of the state. The objective is to calculate a 95% confidence interval for the proportion of all Californians who considered moving out of state, given the sample size and proportion.
B. The formula to calculate the confidence interval for a proportion is:
CI = p^ ± z* √[(p^(1-p^))/n]
Where p^ is the sample proportion, n is the sample size, and z* is the critical value of the standard normal distribution for the desired confidence level. For a 95% confidence level, z* = 1.96.
Substituting the given values into the formula, we get:
CI = 0.517 ± 1.96 * √[(0.517*(1-0.517))/4527]
CI = 0.517 ± 0.013
The 95% confidence interval for the proportion of all Californians who considered moving out of state is (0.504, 0.530). Therefore, we can be 95% confident that the true proportion of all Californians who considered moving out of state lies between 50.4% and 53.0%.
For more questions like Sample click the link below:
https://brainly.com/question/31101410
#SPJ11
Which functions are increasing?
Select all answers that are correct.

Answers
Answer:
Step-by-step explanation:

Find the value of x and y.

Answers
Answer:
x= 73
y= 13
Step-by-step explanation:
The sum of the angles opposite the exterior angle = the exterior angle so
x= 141-68
x= 73
The angle sum of a triangle= 180.
180-68-73= 39
since there are 3 "y"s we need to divide 39 by 3
39/3= 13
The lengths of pregnancies in a small rural village are normally distributed with a mean of 270 days and a standard deviation of 14 days. In what range would you expect to find the middle 98% of most pregnancies
Answers
We would expect to find the middle 98% of most pregnancies in the small rural village in the range of approximately 237 to 303 days.
We can use the properties of the normal distribution to determine the range in which we would expect to find the middle 98% of most pregnancies in the small rural village.
First, we need to find the z-scores associated with the upper and lower tails of the distribution that exclude the middle 2%. We can use a standard normal distribution table or calculator to find these values:
For the upper tail, the z-score is 2.33 (corresponding to a probability of 0.01 or 1%).
For the lower tail, the z-score is -2.33 (corresponding to a probability of 0.01 or 1%).
Next, we can use the formula for transforming a z-score into an actual value:
z = (x - μ) / σ
where z is the z-score, x is the actual value, μ is the mean, and σ is the standard deviation.
Substituting the values we know, we can solve for the upper and lower limits of the range:
For the upper limit:
2.33 = (x - 270) / 14
x - 270 = 32.62
x = 302.62
For the lower limit:
-2.33 = (x - 270) / 14
x - 270 = -32.62
x = 237.38
for such more question on z-score
https://brainly.com/question/15222372
#SPJ11
The table shows the monthly revenue of a business rising exponentially since it opened an online store.
b. Write an equation to represent the revenue, R, as a function of months, m, since the online store opened.

Answers
The monthly revenue of the business grows by 8%, monthly.
The definition of revenue?
The total income a firm receives from the sale of products or services that are connected to its core business operations is referred to as revenue.
Since it appears at the top of the income statement, revenue, also known as gross sales, is frequently referred to as the "top line." An organization's whole earnings or profit is known as income, or net income.
An exponential function is represented as
y = abˣ
From the table we have the following ordered pair
(x,y) = {(0,72000) (3,90000)}
So, we have
90000 = 72000 * b³
Divide both sides by 72000
b³ = 1.25
Take the cube roots of both sides
b = ∛1.25
b = 1.08
Recall that
b = 1 +r
1 + r = 1.08
r = 0.08
r = 8%
Hence, the monthly revenue of the business grows by 8%, monthly.
Learn more about revenue
brainly.com/question/29567732
#SPJ1
The height of the cuboid is 10 cm. Its length is 3 times its height and 5 times its width. Find the volume of the cuboid. The volume of the cuboid is cm³ Enter the answer Check it
Answers
In this case, the height is given as 10 cm, the length is 3 times the height, and the width is 1/5 of the length. By substituting these values into the formula for the volume of a cuboid is 1800 cm³.
To find the volume of the cuboid, we need to know its height, length, and width. Let's calculate the volume of the cuboid using the given information. We know that the height of the cuboid is 10 cm.
The length of the cuboid is given as 3 times the height. So, the length = 3 * 10 cm = 30 cm.
The width of the cuboid is stated as 1/5 of the length. Therefore, the width = (1/5) * 30 cm = 6 cm.
To find the volume of the cuboid, we use the formula: Volume = length * width * height. Substituting the values we found, the volume = 30 cm * 6 cm * 10 cm = 1800 cm³.
Therefore, the volume of the cuboid is 1800 cm³.
To learn more about volume of a cuboid click here
brainly.com/question/28770143
#SPJ11
Is y a function of x? Or not?
And explain?

Answers
Answer:
Y is NOT a function of X
Step-by-step explanation:
I guess this because it doesn't go in a pattern.
what is u = kx + ух, for x
Answers
Answer:
\(x= \frac{u}{k + y} \)Step-by-step explanation:
u = kx + ух
First of all factorize x out at the right side of the equation
That's
u = x(k + y)
Divide both sides by ( k + y) to make x stand alone
That's
\( \frac{x(k + y)}{k + y} = \frac{u}{k + y} \)We have the final answer as
\(x = \frac{u}{k + y} \)Hope this helps you
Each square on a grid represents 1 unit on each side. Match the numbers with the slopes of the lines.

Answers
The slope of the given lines are:
Graph 1 = 1/3
Graph 2 = -1/3
Graph 3 = 3
Graph 4 = -3
How to Find the Slope of a Line?To find the slope (m) of a given line on a coordinate plane, choose any two points on the line, (x1, y1) and (x2, y2), then find the slope by plugging in the values of the coordinates into the formula below:
Slope of a line (m) = change in y / change in x = \(\frac{y_2 - y_1}{x_2 - x_1}\).
Find the slope of Graph 1:
Using two points on the line, (0, 0) and (3, 1):
Slope of graph 1 (m) = (1 - 0)/(3 - 0)
Slope of graph 1 (m) = 1/3
Find the slope of Graph 2:
Using two points on the line, (0, 0) and (-3, 1):
Slope of graph 2 (m) = (1 - 0)/(-3 - 0) = 1/-3
Slope of graph 2 (m) = -1/3
Find the slope of Graph 3:
Using two points on the line, (0, 0) and (1, 3):
Slope of graph 3 (m) = (3 - 0)/(1 - 0) = 3/1
Slope of graph 3 (m) = 3
Find the slope of Graph 4:
Using two points on the line, (0, 0) and (-1, 3):
Slope of graph 4 (m) = (3 - 0)/(-1 - 0) = 3/-1
Slope of graph 4 (m) = -3
Learn more about slope on:
https://brainly.com/question/13861479
#SPJ1
What is the slope of a line that is perpendicular to the line y= -1/2x + 5?
A. -2
B. -1/2
C. 1/2
D. 2
Answers
Answer: on else beans or torti
bestiesss helpsss plsss
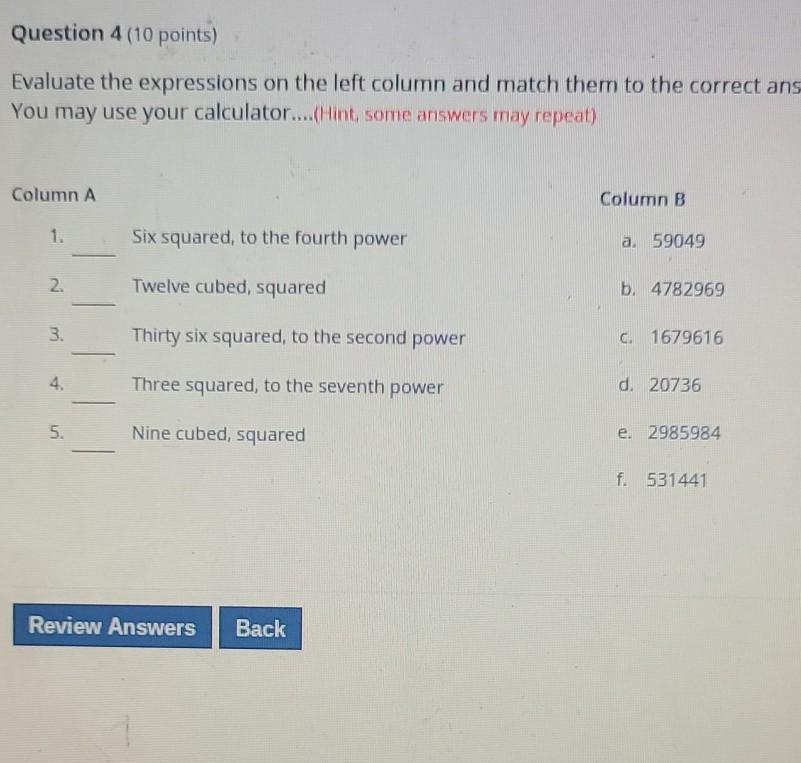
Answers
(6^2)^4
(12^3)^2
(36^2)^2
(3^2)^7
(9^3)^2
Solve each equation. Check your answers.
|2 y-3|=12
Answers
The solutions to the equation |2y-3|=12 are y=7.5 and y=-4.5.
To solve the equation |2y-3|=12, we need to eliminate the absolute value by considering both the positive and negative cases.
In the positive case, we have 2y-3=12. Adding 3 to both sides gives us 2y=15, and dividing by 2 yields y=7.5.
In the negative case, we have -(2y-3)=12. Distributing the negative sign gives -2y+3=12. Subtracting 3 from both sides gives -2y=9, and dividing by -2 yields y=-4.5.
Therefore, the possible solutions are y=7.5 and y=-4.5. To verify these solutions, we substitute them back into the original equation.
For y=7.5, we have |2(7.5)-3|=12. Simplifying, we get |15-3|=12, which is true since the absolute value of 15-3 is 12.
For y=-4.5, we have |2(-4.5)-3|=12. Simplifying, we get |-9-3|=12, which is also true since the absolute value of -9-3 is 12.
Hence, both solutions satisfy the original equation, confirming that y=7.5 and y=-4.5 are the correct solutions.
Learn more about equation here: brainly.com/question/29538993
#SPJ11
Tim bought some cans of paint and 3/4 of a liter of special paint additive formulated to reduce mildew. Before painting his house, he used all of the additive to put 3/8 of a liter of additive in each can. How many cans of paint did Tim buy?

Answers
If Tim bought some cans of paint and 3/4 of a liter of special paint additive formulated to reduce mildew. Before painting his house, he used all of the additive to put 3/8 of a liter of additive in each can. The number of cans of paint that Tim buy is: 6 cans.
Number of can of paints boughtLet x represent the number of can
Quantity of addictive mixed in each liter=3/8
Total addictive mixed=3/4
Hence,
x(3/8)=3/4
Cross multiply
x=8(3/4)
x=6 cans of paint
Therefore If Tim bought some cans of paint and 3/4 of a liter of special paint additive formulated to reduce mildew. Before painting his house, he used all of the additive to put 3/8 of a liter of additive in each can. The number of cans of paint that Tim buy is: 6 cans.
Learn more about Number of can of paints bought here:https://brainly.com/question/28183343
#SPJ1