To complete the container label, Gordon needs to know the lateral surface area of the container. The lateral surface area is found using , where is the radius of the container’s base, and is the slant height. What is the lateral surface area of the container? Round to the nearest hundredth, if necessary. Show your work.
Answers
Based on the radius of the container's base, and the slant height, the lateral surface area would be 21.23 in².
How can the lateral surface area be found?= π x radius x slant height
The slant height is:
Cos BAC = BA / Slant height or AC
Cos 72° = 2 / AC
AC = 2 / Cos 72°
= 6.47 inch
The lateral surface is:
= 22/7 x 2 x 6.47
= 40.67 inch²
First part of question:
Gordon works for a graphic design firm and is creating a label for a food truck vendor. The vendor specializes in finger food and wants to sell food in right conical containers so they're easy for people to hold. To complete his label, Gordon needs to collect several different measurements to ensure that the label he designs will fit the surface of the container. Gordon has been given a model of the container and told that the diameter is 4 inches and the measure of angle BAC in the model is 72°.
Find out more on lateral surface area at https://brainly.com/question/15476307.
#SPJ1
Related Questions
Given that at least one card is a king, what is the conditional probability that at least one card is a diamond? (a) 0.250 (b) 0.333 (c) 0.389 (d) 0.443
Answers
To calculate the conditional probability that at least one card is a diamond given that at least one card is a king, we can use the formula P(A|B) = P(A ∩ B) / P(B), where A is the event "at least one card is a diamond" and B is the event "at least one card is a king".
P(A ∩ B) is the probability of both events occurring, meaning there is at least one King of Diamonds. Since there is only one King of Diamonds in a deck of 52 cards, P(A ∩ B) = 1/52.
P(B) is the probability that at least one card is a king. There are 4 kings in a deck of 52 cards, so P(at least one king) = 1 - P(no kings). There are 48 non-king cards, so P(no kings) = (48/52)*(47/51) = 0.8235. Therefore, P(B) = 1 - 0.8235 = 0.1765.
Now, we can find the conditional probability P(A|B): P(A|B) = P(A ∩ B) / P(B) = (1/52) / 0.1765 = 0.333.
So, the answer is (b) 0.333.
To know more about conditional probability refer here
https://brainly.com/question/10567654#
#SPJ11
A supplier regularly ships spare bulbs in bulk to the theater and promises a 95% reliability (lasting at least 100 hours). The theater inspects each incoming shipment of bulbs by lighting 20 bulbs for 100 hours. If two or more bulbs go out during the test, the batch shipment is returned to the supplier. If the bulbs indeed have a 95% reliability, what is the likelihood that a shipment passes the test?
Serial and parallel systems reliability concept
Answers
The likelihood that a shipment passes the test is 1
To determine the likelihood that a shipment passes the test, we can approach this problem using the concept of reliability in parallel systems.
In this case, the theater is testing a batch shipment of bulbs, and if two or more bulbs go out during the test, the shipment is returned. We can consider each bulb's reliability as an independent event.
The reliability of a single bulb is given as 95%, which means the probability that a bulb lasts at least 100 hours is 0.95. Therefore, the probability that a single bulb fails during the test (lasting less than 100 hours) is 1 - 0.95 = 0.05.
Since the theater tests 20 bulbs in parallel, we can consider it as a parallel system. In a parallel system, the overall system fails if and only if all the components fail. So, for the shipment to fail the test, all 20 bulbs must fail.
The probability that a single bulb fails during the test is 0.05. Since the bulbs are independent, we can multiply the probabilities:
Probability that all 20 bulbs fail = (0.05) * (0.05) * ... * (0.05) (20 times)
= 0.05^20
≈ 9.537 × 10^(-27)
Therefore, the likelihood that a shipment passes the test is the complement of the probability that all 20 bulbs fail:
Probability that a shipment passes the test = 1 - Probability that all 20 bulbs fail
= 1 - 9.537 × 10^(-27)
≈ 1
In practical terms, the likelihood that a shipment passes the test is essentially 1 (or 100%). This means that if the bulbs indeed have a 95% reliability, it is highly unlikely that two or more bulbs would go out during the test, and the shipment would almost always pass the test.
Learn more about the probability visit:
brainly.com/question/13604758
#SPJ11
What is the length of CD in this diagram, ABC - EDC,

Answers
Answer:
4Option A is the right option.
solution,
∆ABC~∆EDC
\( \frac{bc}{cd} = \frac{ac}{ec} \\ \: \)
putting the values,
\( \frac{20 - x}{x} = \frac{20}{5} \\ or \: 5(20 - x) = 20x(cross \: multiplication) \\ or \: 100 - 5x = 20x \\ or \: - 5x - 20x = - 100 \\ or \: \: - 25x = - 100 \\ \: or \: x = \frac{ - 100}{ - 25} \\ x = 4\)
Hope this helps..
Good luck on your assignment..
Please help I would really appreciate it

Answers
Answer:
50°
Step-by-step explanation:
Sum of interior angle is equal to the sum of exterior angle
Two whole number, three over five of the pupils in a school are boys. If there are 96 girls and the school,how many pupils are there in the school?
Answers
Answer:
106 students
Step-by-step explanation:
If you take the 2 3/5 and covert it into a whole number by: 2×3+5 = 10
and then you have 96 girls so you add the whole number you got that is 10 and the 96 girls
=96+10= 106 students
⋆ ˚。⋆୨୧˚hope this helped˚୨୧⋆。˚ ⋆
In the U.S., shoe sizes are defined differently for men and women, but in Europe, both sexes use the same shoe size scale. The accompanying histogram shows the European shoe sizes of 269 male and female college students, converted from their reported U.S. shoe sizes. What might be the problem with either the mean or the median as a measure of center?
Answers
To accurately represent the shoe sizes for men and women separately, it would be better to compute the mean or median shoe size for each group separately and compare them.
The problem with either the mean or the median as a measure of center in this case is that the data is not separated by gender, and the shoe size distributions for men and women are likely to be different. Therefore, computing the mean or median shoe size across all students may not accurately represent the typical shoe size for men or women separately.
For example, if the men in the sample have, on average, larger shoe sizes than the women, then the mean shoe size across all students may be biased towards the larger sizes, even though the majority of the students are women. On the other hand, if there are a few male students with very large shoe sizes, then the median shoe size across all students may be biased towards the larger sizes as well, even if most of the students are women with smaller shoe sizes.
To accurately represent the shoe sizes for men and women separately, it would be better to compute the mean or median shoe size for each group separately and compare them. Alternatively, a better measure of center might be to report the mode, which represents the most common shoe size in the data.
Learn more about median here https://brainly.com/question/28060453
#SPJ4
Alyssa surveys her freshman math class to determine their favorite tv show
Answers
The number of students who watch between 1 - 2 hours is 9.
We have,
From the table,
Number of students who watch tv for 1 hour = 5
Number of students who watch tv for 1.5 hours = 3
Number of students who watch tv for 2 hours = 1
Now,
The number of students who watch between 1 - 2 hours.
= Number of students who watch tv for 1 hour + 1.5 hours + 2 hours
= 5 + 3 + 1
= 9
Thus,
The number of students who watch between 1 - 2 hours is 9.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ4

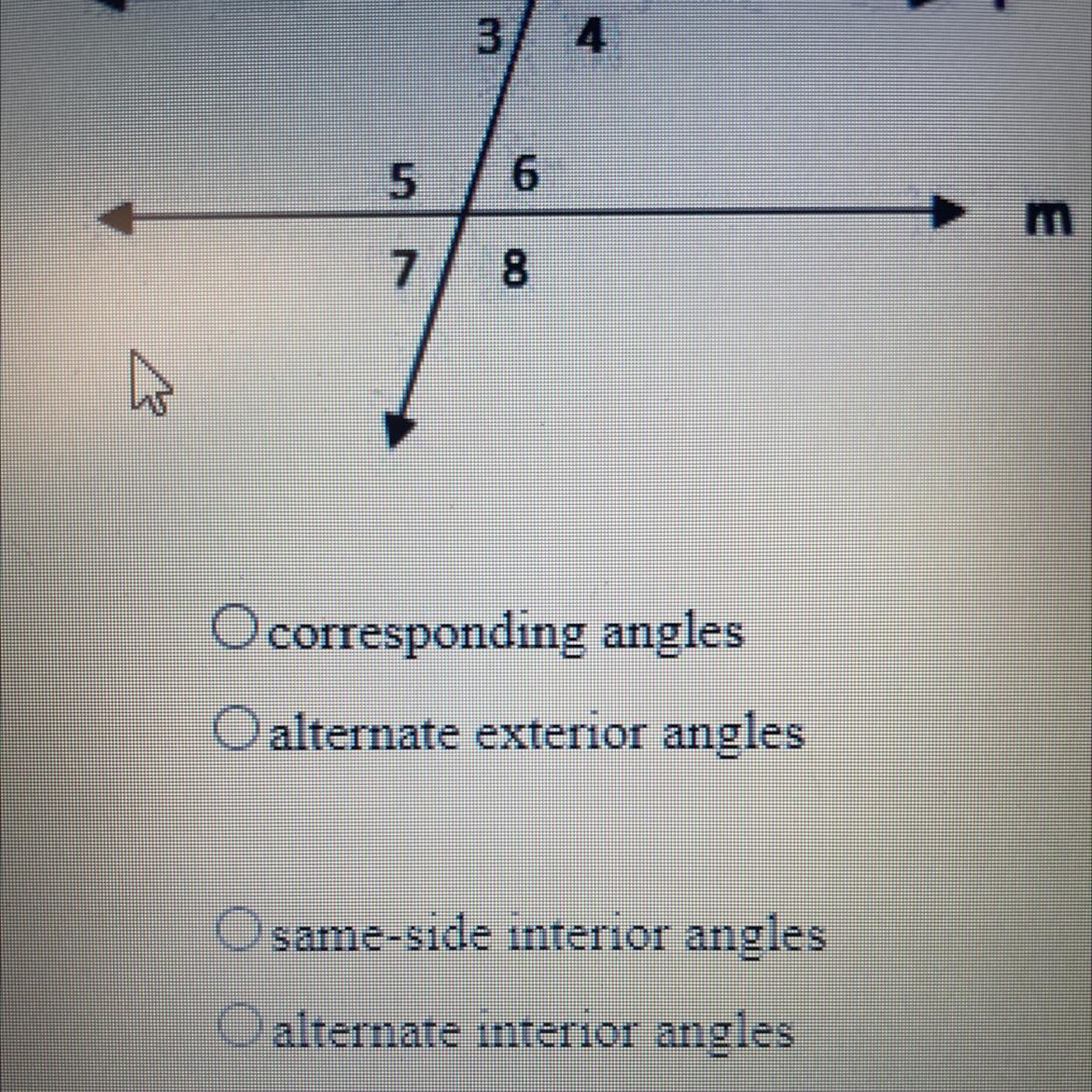
please help me with these questions
Problem 1: Find the measure of each marked angle. 2. (7x+19) (2x-1)º "V Vest (-3x+5)° (-8x+30) 5. 6. (32-2x)" (10x-10) (2x+18) (8x+14) (12x+40) (20x + 10) mand n are parallel. Problem 2: Identify th
Answers
In Problem 1, the measure of each marked angle is as follows:292º, -112º, -282º, -46º, 380º, 96º, 326º, 508º, and 790º.In Problem 2, the angles indicated by the letters in the given figure are as follows:c = 65º, d = 95º, e = 65º, f = 95º, g = 85º, and h = 85º.
Problem 1:The measures of the marked angles are as follows:(7x + 19)º and (-3x + 5)º are supplementary angles since they are the interior angles on the same side of the transversal "V Vest".
Therefore, we can say: (7x + 19)º + (-3x + 5)º = 180º Simplifying, 7x + 19 - 3x + 5 = 180
Combine like terms and solve for x: 4x + 24 = 180 4x = 180 - 24 4x = 156 x = 39 Now substitute x = 39 in the given expressions and find the value of each angle.
(7x + 19)º = (7 × 39 + 19)º = 292º(-3x + 5)º
= (-3 × 39 + 5)º = -112º(-8x + 30)º = (-8 × 39 + 30)º
= -282º(32 - 2x)º = (32 - 2 × 39)º = -46º(10x - 10)º
= (10 × 39 - 10)º = 380º(2x + 18)º = (2 × 39 + 18)º = 96º(8x + 14)º
= (8 × 39 + 14)º = 326º(12x + 40)º = (12 × 39 + 40)º
= 508º(20x + 10)º = (20 × 39 + 10)º = 790º
Therefore, the measures of the marked angles are:292º, -112º, -282º, -46º, 380º, 96º, 326º, 508º, and 790º.Problem 2:The angles indicated by the letters in the given figure are as follows: Angle c: Corresponding angles with respect to the parallel lines n and m are equal. Therefore, we can say: c = 65º.Angle d: Vertically opposite angles are equal. Therefore, we can say: d = 95º.
Angle e: Alternate interior angles with respect to the parallel lines n and m are equal. Therefore, we can say: e = 65º.Angle f: Corresponding angles with respect to the parallel lines n and m are equal. Therefore, we can say: f = 95º.Angle g: Interior angles on the same side of the transversal are supplementary. Therefore, we can say: g = 180º - 95º = 85º.Angle h: Vertically opposite angles are equal. Therefore, we can say: h = 85º.
To know more about angle visit:-
https://brainly.com/question/31818999
#SPJ11
Solve for a. 5+14a=9a-4
Answers
Answer:
Isolate the variable by dividing each side by factors that don't contain the variable.
Step-by-step explanation:
Exact Form:
a=−9/5
Decimal Form:
a=−1.8
Mixed Number Form:
a=−1 4/5
if 1 cm represents 35 miles what is 1.25 cm in miles?
Answers
Answer:
43.75 miles
Step-by-step explanation:
You divide the 35 by 4 and then just add it to the original distance of 35 miles. 35/4=8.75
8.75+35=43.75
i will give u brainliest

Answers
Answer:
The reciprocal of 2 is 1/2
The reciprocal of 6/11 is 11/6
help fast i need this

Answers
Answer:
74
Step-by-step explanation:
answer: 74
explanation: hope it helped
Solve
10/r > 1; r = 5
Answers
Answer:
10/5 = 2
so its 2>1
Step-by-step explanation:
How do you solve 10 - x = 25?
Answers
Answer:
Work the problem backward
Step-by-step explanation:
instead of 10-x=25 do 25-10 = x So yeah that should give you the variable X
Answer:
-15
Step-by-step explanation:
10-x=25
take away 10 from both sides of the equation.
-x = 15
divide by - (-1) to get x
x = -15
Describe the transformation of y=f(x) for the new function f(x)=2/3|x-7|

Answers
Answer:
Stretch of 2/3, right by 7
Suppose the heights of the members of a population follow a normal distribution. If the mean height of the population is 72 inches and the standard deviation is 3 inches, 68% of the population will have a height within which range? A. 59 inches to 71 inches B. 53 inches to 77 inches C. 62 inches to 68 inches D. 56 inches to 74 inches
Answers
68% of the population will have a height within the range of 69 inches to 75 inches. None of the provided options match this range.
Calculating Range using Mean and Standard DeviationIn a normal distribution, approximately 68% of the values fall within one standard deviation of the mean.
Given:
mean height = 72 inches
standard deviation = 3 inches,
We can determine the range within which 68% of the population's heights will fall.
To calculate this range, we subtract and add one standard deviation from the mean:
Lower bound: Mean - Standard Deviation
= 72 - 3
= 69 inches
Upper bound: Mean + Standard Deviation
= 72 + 3
= 75 inches
Therefore, 68% of the population will have a height within the range of 69 inches to 75 inches.
Learn more about standard deviation here:
https://brainly.com/question/24298037
#SPJ1
help a girl out pleaseeeeeeeeeeeeee

Answers
Answer:
\(k=-\frac{2}{5}\)
Step-by-step explanation:
\(k=-\frac{8}{20}=-\frac{4(2)}{4(5)}=-\frac{2}{5}\)
Answer: y = -32 and -(2/5)
Step-by-step explanation:
Let z equal to the difference,
x - z = -4
20 - z = -4
20 + 4 = z
z = 24
y - z
= -8 - 24
= -32
Therefore y = -32
For the second part of the question
-8 = k(20)
-8 = k * 20
-8/20 = k <-- Divide both sides by 20
Therefore k = -(8/20) = -(2/5)
A shirt you like has a list price of $40.00. Today only, it is on sale at 35% off.
What is the sale price?
Answers
math help quickly and pls no links lol

Answers
6. Devon draws one marble from
a bag containing 5 red, 3 green,
and 4 yellow marbles. What is the
probability that Devon draws a
green marble?
Answers
Answer: Probability: 3/12 or 1/4
Step-by-step explanation:
The base of a triangular pyramid is an equilateral triangle. Each side of the base measures 12 in. The area of the base is 62.4 in². The slant height of the pyramid is 6 in.
What is the surface area of the pyramid?
Enter your answer in the box.

Answers
The surface area of the pyramid is given by the equation A = 170.4 inches²
What is the surface area of the pyramid?The total surface area is the summation of the areas of the base and the three other sides. A = B + ( 1/2 ) ( P x h ), where B is the area of the base of the pyramid, P is the perimeter of the base, and h is the slant height of the pyramid
Surface Area of Pyramid = B + ( 1/2 ) ( P x h )
Given data ,
Let the surface area of the pyramid be represented as A
Now , the equation will be
The slant height of the pyramid h = 6 inches
The side of the equilateral triangle = 12 inches
So , the perimeter of the triangle = 3 x side length
Substituting the values in the equation , we get
The perimeter of the triangle = 36 inches
The area of the base = 62.4 inches²
So , Surface Area of Pyramid = B + ( 1/2 ) ( P x h )
Substituting the values in the equation , we get
Surface Area of Pyramid = 62.4 + ( 1/2 ) ( 36 x 6 )
On simplifying the equation , we get
Surface Area of Pyramid = 62.4 + ( 108 )
Surface Area of Pyramid = 170.4 inches²
Hence , the surface area of pyramid is 170.4 inches²
To learn more about surface area of pyramid click :
https://brainly.com/question/15050758
#SPJ1
Imagine some DEQ: y'=f(x,y), which is not given in this exercise.
Use Euler integration to determine the next values of x and y, given the current values: x=2, y=8 and y'=9. The step size is delta_X= 5. 2 answers
Refer to the LT table. f(t)=6. Determine tNum,a,b and n. 4 answers
Answers
Using Euler integration, the next values of x and y can be determined as follows:
x_next = x_current + delta_X
y_next = y_current + delta_X * y'
What are the updated values of x and y using Euler integration?Euler integration is a numerical method used to approximate solutions to differential equations. It is based on the concept of dividing the interval into small steps and using the derivative at each step to calculate the next value. In this case, we are given the current values of x=2, y=8, and y'=9, with a step size of delta_X=5.
To determine the next values of x and y, we use the following formulas:
x_next = x_current + delta_X
y_next = y_current + delta_X * y'
Substituting the given values into the formulas, we have:
x_next = 2 + 5 = 7
y_next = 8 + 5 * 9 = 53
Therefore, the updated values of x and y using Euler integration are x=7 and y=53.
It's important to note that Euler integration provides an approximate solution and the accuracy depends on the chosen step size. Smaller step sizes generally lead to more accurate results. Other numerical methods, such as Runge-Kutta methods, may provide more accurate approximations.
Learn more about integration
brainly.com/question/30900582
#SPJ11
I need answers for this question

Answers
The inequality 3 ≤ x - 2 simplifies to x ≥ 5. This means x can take any value greater than or equal to 5. Therefore, option (E) with a number line from positive 5 to positive 10 is correct.
Given: 3 \(\leq\) x - 2
We need to work out which number line below shows the values that x can take. In order to solve the inequality, we will add 2 to both sides. 3+2 \(\leq\) x - 2+2 5 \(\leq\) x
Now the inequality is in form x \(\geq\) 5. This means that x can take any value greater than or equal to 5. So, the number line going from positive 5 to positive 10 shows the values that x can take.
Therefore, the correct option is (E) A number line going from positive 5 to positive 10. We added 2 to both sides of the given inequality, which gives us 5 \(\leq\) x. It shows that x can take any value greater than or equal to 5.
Hence, option E is correct.
For more questions on inequality
https://brainly.com/question/30238989
#SPJ8
Leslie took 60 wooden blocks and arranged them in 10 even stacks. How many blocks are in each stack?
Answers
Leslie arranged 6 blocks in each of the 10 stacks.
a large solid piece of hard material, especially rock, stone, or wood,
typically with flat surfaces on each side.Full Definition of block (Entry 1 of
3) 1 : a compact usually solid piece of substantial material especially
when worked or altered to serve a particular purpose a block of ice
blocks of cheese : such as a : the piece of wood on which the neck of a
person condemned to be beheaded is laid for execution put her neck on
the block.
Leslie took 60 wooden blocks and arranged them in 10 even stacks.
A good answer would be:
Leslie took 60 wooden blocks and arranged them in 10 even stacks.
To find out how many blocks are in each stack,
we can divide the total number of blocks (60) by the number of stacks (10).
60 blocks ÷ 10 stacks = 6 blocks per stack
Therefore, Leslie arranged 6 blocks in each of the 10 stacks.
for such more question on blocks
https://brainly.com/question/14065401
#SPJ11
What is the right translation of these expressions and equations? (with solution)
1. 7 - 2m
2. 3( m + 2) = 15
3. 5m - m(2 - m)
Answers
Answer:
7 - 2m can be translated to "7 minus two times m" or "the difference between 7 and twice m".
3(m + 2) = 15 can be translated to "three times the sum of m and 2 is equal to 15" or "the product of 3 and the sum of m and 2 is 15".
To solve the equation, we can start by distributing the 3 on the left side:
3(m + 2) = 15
3m + 6 = 15
Then, we can subtract 6 from both sides:
3m + 6 - 6 = 15 - 6
3m = 9
Finally, we can divide both sides by 3:
3m/3 = 9/3
m = 3
Therefore, the solution to the equation 3(m + 2) = 15 is m = 3.
5m - m(2 - m) can be translated to "5m minus the product of m and the difference between 2 and m" or "the difference between 5m and m times the quantity 2 minus m".
To simplify the expression, we can use the distributive property to expand the second term:
5m - m(2 - m) = 5m - 2m + m^2 = m^2 + 3m
Therefore, the simplified expression is m^2 + 3m.
What is the relationship between 23 and 26?
Answers
3. Consider the following system: →0.85→0.85→ Determine the probability that the system will operate under each of these conditions: a. The system as shown. (Do not round your intermediate calculations. Round your final answer to 4 decimal places.) b. Each system component has a backup with a probability of .85 and a switch that is 100 percent reliable. (Do not round your intermediate calculations. Round your final answer to 4 decimal places. c. Each system component has a backup with a probability of .85 and a switch that is 90 percent reliable. (Do not round your intermediate calculations. Round your final answer to 4 decimal places.)
Answers
a. The probability that the system will operate as shown is approximately 0.6141.
b. Probability ≈ 0.6141The probability remains the same as in the previous case, which is approximately 0.6141.
c. The probability that the system will operate with each component having a backup with a probability of 0.85 and a switch that is 90% reliable is approximately 0.6485.
a. To find the probability that the system will operate as shown, we multiply the probabilities of each component. Since the system is shown to have three components with a probability of 0.85 each, we can calculate:
Probability = 0.85 × 0.85 × 0.85
Probability ≈ 0.6141
The probability that the system will operate as shown is approximately 0.6141.
b. In this case, each system component has a backup with a probability of 0.85 and a switch that is 100% reliable. Since the backup has a probability of 0.85, and the switch is 100% reliable (probability = 1), we can calculate the probability as:
Probability = 0.85 × 0.85 × 0.85
Probability ≈ 0.6141The probability remains the same as in the previous case, which is approximately 0.6141.
c. In this scenario, each system component has a backup with a probability of 0.85, but the switch is 90% reliable (probability = 0.90). We can calculate the probability as:
Probability = 0.85 × 0.90 × 0.85
Probability ≈ 0.6485
The probability that the system will operate with each component having a backup with a probability of 0.85 and a switch that is 90% reliable is approximately 0.6485.
For more such questions on Probability
https://brainly.com/question/30390037
#SPJ8
Find the product and simplify. (3c-5) ^2
Answers
Answer:
9c² -30c + 25
Step-by-step explanation:
Perfect square trinomial: (a - b)² = a² - 2ab + b²
(3c - 5)²
(3c)² -2(3c * 5) + 5²
9c² -2(15c) + 5²
9c² -30c + 25
Final answer: 9c² -30c + 25
Hope this helps!
Hi!
Given:
\((3c-5)^2\)
As this is squared, we are simply multiplying the given expression by itself, like so:
\((3c-5)(3c-5)\)
Now, we can use the Distributive Property to solve, using the FOIL Method:
\((3c-5)(3c-5)\)
\(9c^2-15c-15c+25\)
Combine like terms:
\(9c^2-30c+25\)
For a similar problem, see:
https://brainly.com/question/15639394

A line passes through the points (−4, −18) and (0, 2). Which is an equation of the line?
Answers
Answer:
y=5x+2
Step-by-step explanation:
First of all, remember what the equation of a line is:
y = mx+b
Where:
m is the slope, and
b is the y-intercept
First, let's find what m is, the slope of the line...
The slope of a line is a measure of how fast the line "goes up" or "goes down". A large slope means the line goes up or down really fast (a very steep line). Small slopes means the line isn't very steep. A slope of zero means the line has no steepness at all; it is perfectly horizontal.
For lines like these, the slope is always defined as "the change in y over the change in x" or, in equation form:
So what we need now are the two points you gave that the line passes through. Let's call the first point you gave, (-4,-18), point #1, so the x and y numbers given will be called x1 and y1. Or, x1=-4 and y1=-18.
Also, let's call the second point you gave, (0,2), point #2, so the x and y numbers here will be called x2 and y2. Or, x2=0 and y2=2.
Now, just plug the numbers into the formula for m above, like this:
m= (2 - -18)
------------
(0 - -4)
or...
m= 20
-------
4
or...
m=5
So, we have the first piece to finding the equation of this line, and we can fill it into y=mx+b like this:
y=5x+b
Now, what about b, the y-intercept?
To find b, think about what your (x,y) points mean:
(-4,-18). When x of the line is -4, y of the line must be -18.
(0,2). When x of the line is 0, y of the line must be 2.
Because you said the line passes through each one of these two points, right?
Now, look at our line's equation so far: y=5x+b. b is what we want, the 5 is already set and x and y are just two "free variables" sitting there. We can plug anything we want in for x and y here, but we want the equation for the line that specfically passes through the two points (-4,-18) and (0,2).
So, why not plug in for x and y from one of our (x,y) points that we know the line passes through? This will allow us to solve for b for the particular line that passes through the two points you gave!.
You can use either (x,y) point you want..the answer will be the same:
(-4,-18). y=mx+b or -18=5 × -4+b, or solving for b: b=-18-(5)(-4). b=2.
(0,2). y=mx+b or 2=5 × 0+b, or solving for b: b=2-(5)(0). b=2.
See! In both cases we got the same value for b. And this completes our problem.
The equation of the line that passes through the points
(-4,-18) and (0,2)
is
y=5x+2
write a linear function f with the values f ( - 2 ) = 3 and f ( 5 ) = 7
Answers
You write f (-2) = 3 as (-2, 3) and f (5) = 7 as (5, 7).
The answer for the graph is \(\mathbf{\frac{4}{3}}\textbf{\textit{x}}\mathbf{+\frac{1}{3}}\).