this is my last question for the night please answer !!!!! yes 49 points you earn if u answer

Answers
Steps:
4.75X = 21-3
4.75X = 19
19 / 4.75
X=4
Related Questions
Marissa is ordering Negative one-sixth, negative one-third, 1.4, 0.2, two-thirds from least to greatest. Here are her steps: (1) Write each decimal as a fraction. (2) Write every fraction with a common denominator of 18. (3) Plot the numbers on the number line. (4) List the numbers from left to right as they are plotted on the number line. Identify any and all errors that Marissa made in her steps. Marissa should have only plotted the fractions on the number line. Marissa should have used 30 as the common denominator. Marissa should have listed the numbers from right to left after she plotted them on the number line. Marissa should have used a common denominator of 30 and should have listed the numbers from right to left after she plotted them on the number line.
Answers
Answer:
Marissa should have used 30 as the common denominator.
Step-by-step explanation:
Looking at the numbers to be listed:
–1/6
–1/3
1.4 = 14/10 = 7/5
0.2 = 2/10 = 1/5
2/3
Looking for the LCM of 6, 3, 7/5, 1/5 and 3 we get 30.
Since the numbers are to be listed from least to greatest, then ordering from left to right is the correct form of listing since the numbers on the number line increase going from left to right.
This implies that the only mistake she made was she should've used 30 as the common denominator.
Answer:
BStep-by-step explanation:
HOPE IT HELPS!
ind the acute angle between the lines. round your answer to the nearest degree. 2x − y = 3, 7x y = 9
Answers
The acute angle between the two lines is approximately 36.87°
The question asks to find the acute angle between two lines given by the equations 2x - y = 3 and 7x + y = 9.
To find the acute angle between two lines, we can use the formula:
angle = arctan(|m1 - m2| / 1 + m1 × m2)
where m1 and m2 are the slopes of the two lines.
First, we need to convert the given equations into slope-intercept form (y = mx + b).
2x - y = 3 => y = 2x - 3 (slope = 2)
7x + y = 9 => y = -7x + 9 (slope = -7)
Now we can substitute the slopes into the formula and simplify:
angle = arctan(|2 - (-7)| / 1 + (2 × -7))
= arctan(9 / -12)
= arctan(-0.75)
≈ -36.87°
Note that the arctan function gives an angle in radians, so we converted it to degrees using the fact that 180°/π radians ≈ 57.2958°/rad.
Therefore, the acute angle between the two lines is approximately 36.87°
To learn more about acute angle here:
brainly.com/question/4022946#
#SPJ11
A teacher places 10 marbles in a bag.
- 2 blue marbles
- 3 red marbles
- 5 yellow marbles
A student draws one marble from the bag, does not replace it, then draws another marble from the bag. What is the probability that the first marble will be yellow and the second marble will be red?
Answers
Step-by-step explanation:
Since they do not replace it the total amount of marbles are the same
The function f(x)f(x) is graphed below. Determine whether the degree of the function is even or odd and whether the function itself is even or odd.

Answers
Answer:
The degree is even and the function is even.
Step-by-step explanation:
The graph is a parabola, indicating that the degree is even.
The defintion of an even function is that f(x)=f(-x), and by observing the graph of the function, we will be able to verify that f(x)=f(-x). It is therefore an even function.
The degree of the function is even and the function will be even.
What is a function?A statement, principle, or policy that creates the link between two variables is known as a function. Functions are found all across mathematics and are required for the creation of complex relationships.
The function f(x) is graphed below.
The graph of the function is parabolic whose vertex is at (0, -30). And the curve is passing through the x-axis.
Then the equation of the curve will be
f(x) = ax² - 30
Where a is the leading coefficient.
Then the degree of the function is even and the function will be even.
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ2
Which is the graph of y= 3/4 x - 3?

Answers
Answer:
Graph A.
Step-by-step explanation:
I graphed it out and my graph is below this text.
Have a great day! :D

Evaluate. (Be sure to check by differentiating!) ∫ 8+2x
2
dx,x
=−4 ∫ 8+2x
2
dx= (Type an exact answer. Use parentheses to clearly denote the argument of each function.)
Answers
The answer to the given problem is -32/3.The integral of 8 + 2x^2 with respect to x is equal to 8x + (2/3)x^3 + C. We can determine this by differentiating the antiderivative to obtain the integrand. Setting the antiderivative equal to the given value, we obtain -32/3 as the constant of integration.
We need to evaluate the integral ∫(8+2x^2)dx with the limit x = -4.
We have to find the value of integral using differentiation.
The formula used is as follows ∫(8+2x^2)dx=8x+(2/3)x^3+C (C is the constant of integration)Differentiating the antiderivative of the given function we get; d/dx (8x + (2/3)x^3 + C) = 8 + 2x^2, which is the integrand we started with.
Substituting the given value of -4 in the antiderivative we get,8(-4) + (2/3)(-4)^3 + C = -32/3 + C, where C is a constant that can take on any value.Thus the final answer is -32/3.
Integration is the reverse of differentiation. Differentiation finds the rate of change of a function at any point on its domain while integration finds the accumulated change from the rate of change of the function over a range of its domain.
Integrals come in many forms and are used for solving various problems in mathematics, physics, and engineering. Some common techniques used for finding integrals include substitution, integration by parts, partial fraction decomposition, and trigonometric substitution.
In the given problem, we are to evaluate the integral of the function 8 + 2x^2 with respect to x and find its value at the limit x = -4. Using the formula for finding the antiderivative of this function, we obtain 8x + (2/3)x^3 + C, where C is a constant of integration.
To check our answer, we differentiate this expression to obtain the original integrand. Upon substituting the given value of x, we get -32/3 + C, where C is the constant that can take on any value.
Thus, the answer to the given problem is -32/3.
To learn more about antiderivative
https://brainly.com/question/33243567
#SPJ11
ABC is an isosceles triangle where AB = BC
Find the length marked q on the diagram
give your answer correct to 1 decimal place

Answers
The value of the side q is 2.2
How to determine the valueTo determine the value, we need to take note of the properties of an isosceles triangle. They include;
It has two equal sidesIt has two equal angles, three edges and vertices The sum of interior angles of a triangle equal to 180 degreesUsing the Pythagorean theorem stating that the square of the longest sides of the triangle is equivalent to the sum of the square of the opposite sides as well as the square of the adjacent side.
From the information given, we have;
q² = 2² + 1²
Find the squares
q² = 4 + 1
Add the values, we get;
q² = 5
Find the square root of both sides, we have;
q = 2.2 cm
Learn more about isosceles triangles at: https://brainly.com/question/1475130
#SPJ1
write a function in terms of $t$ that represents the situation. your starting annual salary of $35,000 increases by 4% each year.
Answers
In this problem, the starting annual salary is $35,000 and increases by 4% each year. The task is to write a function in terms of t that represents this situation.
Modeling salary growth over time is a common task in finance and economics.
Let's call the salary after t years s(t).
Then, the salary after t years can be represented by the following function: s(t) = 35,000 * (1 + 0.04t).
This function says that the starting salary of $35,000 is multiplied by (1 + 0.04t) to find the salary after t years.
The constant 0.04 represents the 4% increase each year.
For example, if t = 1, then the salary after 1 year would be $35,000 * (1 + 0.04 * 1) = $36,400, and if t = 2, then the salary after 2 years would be $35,000 * (1 + 0.04 * 2) = $37,888.
Learn more about function here brainly.com/question/12431044
#SPJ4
67+38 (mod5)
pls can someone help me with this question
Answers
Answer:
67 + 38(mod5)
= 67 + 38 =105÷5 (mod5)
= 21 reminder 0 ( mod 5)
Since while handling modes or finites the reminder is always considered therefore;
67 + 38 = 0 ( mod 5)
ST=
Help me please thank u

Answers
Step-by-step explanation:
RS + ST = 8
(RS + ST)×RS = (4 + 2)×4
8 × RS = (4 + 2) × 4 = 6 × 4 = 24
RS = 24/8 = 3
RS + ST = 8
3 + ST = 8
ST = 5
both methods requires two initial guesses x1 and x2, and it is necessary that f(x1)*f(x2) < 0
Answers
The requirement f(x1) * f(x2) < 0 for choosing initial guesses x1 and x2 with opposite signs ensures the validity and convergence of certain numerical root-finding methods such as the bisection method or the regula falsi method.
The statement you provided is true for certain numerical methods used to find roots of equations, such as the bisection method or the regula falsi method. These methods are iterative and require an initial interval or range where the root is expected to be found. To ensure convergence and a valid solution, it is necessary to choose initial guesses x1 and x2 such that the function f(x) evaluated at those points have opposite signs, i.e., f(x1) * f(x2) < 0.
The rationale behind this requirement is based on the Intermediate Value Theorem, which states that if a continuous function f(x) changes sign over an interval [x1, x2], then there exists at least one root within that interval. By ensuring that f(x1) and f(x2) have opposite signs, we guarantee the existence of a root within the interval [x1, x2].
The bisection method works by repeatedly bisecting the interval and selecting a new subinterval that contains the root. At each iteration, the method narrows down the interval by halving it, based on the sign change observed in the function evaluations.
Similarly, the regula falsi (or false position) method also operates by iteratively refining the interval based on the linear interpolation between the function values at the endpoints. The method adjusts the interval based on the sign change of the function, converging to the root.
Both methods rely on the property of opposite signs to guarantee convergence and avoid getting stuck in a non-converging or incorrect solution. If the initial guesses do not satisfy the condition f(x1) * f(x2) < 0, it is possible that the method fails to converge or converges to a different root or solution.
Learn more about bisection method at: brainly.com/question/30320227
#SPJ11
The _____ is used to test the significance of the population coefficient of determination.
A. chi-square distrubution
B. normal distribution
C. Student's t-distribution
D. F-distribution
Answers
The F-distribution is used to test the significance of the population coefficient of determination (option D).
The coefficient of determination, denoted as R², measures the proportion of the variance in the dependent variable that is explained by the independent variables in a regression model. It ranges from 0 to 1, where 0 indicates no relationship and 1 indicates a perfect relationship.
To determine the significance of R², the F-distribution is used. The F-test compares the variation explained by the regression model (numerator) to the unexplained or residual variation (denominator). It calculates the F-statistic, which is the ratio of the two variances.
The F-distribution provides critical values that allow us to determine whether the observed F-statistic is statistically significant or not. By comparing the calculated F-value with the critical value from the F-distribution, we can assess whether the coefficient of determination is significantly different from zero, indicating the presence of a meaningful relationship between the variables. The correct option is d.
To know more about F-distribution:
https://brainly.com/question/14613023
#SPJ4
please someone help me
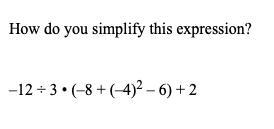
Answers
Answer:
\(( - 12 \div 3) \times ( - 8 + ({ - 4})^{2} - 6) + 2\)
\( = ( - 4) \times ( - 8 + 16 - 6) + 2\)
\( = ( - 4) \times (2) + 2\)
\( = - 8 + 2\)
\( = - 6\)
Step-by-step explanation:
\(( - 12 \div 3) \times ( - 8 + {( - 4)}^{2} + 2 \\ = - 4 \times ( - 8 + 16 - 6) + 2 \\ = - 4 \times ( - 8 + 10) + 2 \\ = - 4 \times 2 + 2 \\ = - 8 + 2 \\ = - 6 \\ thank \: you\)
How do you graph 120=2x+4y?
Answers
you divide everything by 4y which would give you y= 1/2x+ 30
then with a graph you would number your graph and then plot 30 do rise over run and go up one and right two but if there is not space you would go down one and left two
Find the area of the right triangle. If necessary, round to the nearest tenth. A right triangle with side 24 feet and hypotenuse 30 feet. a. 18 square feet b. 216 square feet c. 324 square feet d. 72 square feet
Answers
Answer: 18 square feet im pretty sure
Step-by-step explanation:
Answer: B) 216
Step-by-step explanation:
please please jhelp me....
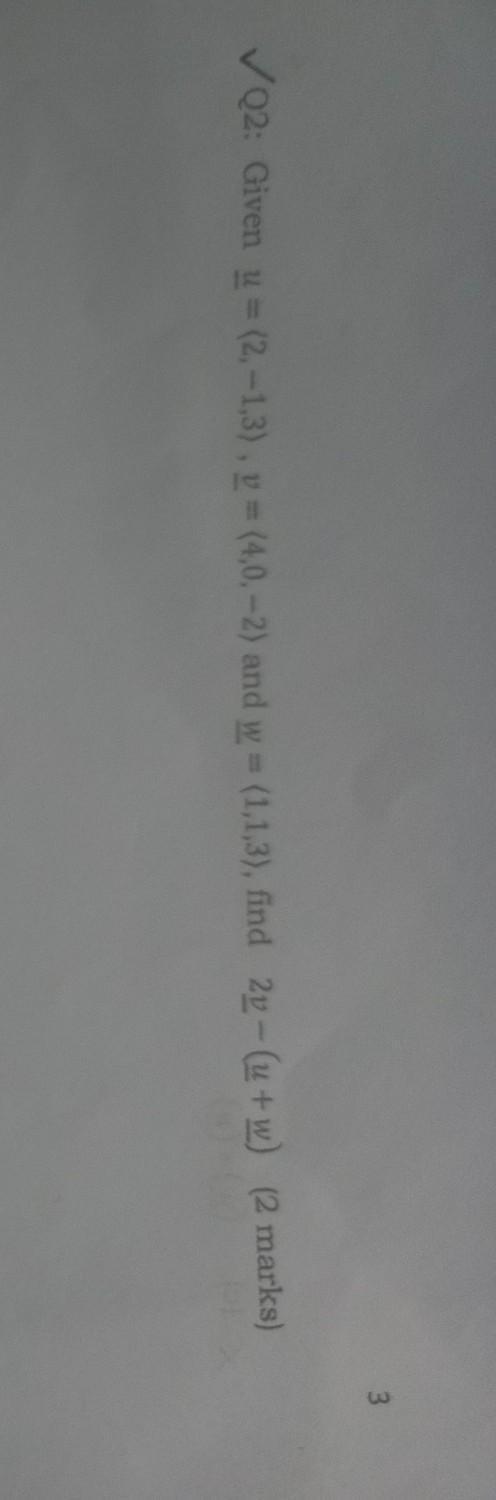
Answers
Answer:
2·v - (u + w) = (5, 0, -10)
Step-by-step explanation:
The given values of the vectors are;
u = (2, -1, 3), v = (4, 0, -2), and w = (1, 1, 3)
The required vector is 2·v - (u + w)
2 × v = 2 × (4, 0, -2) = (8, 0, -4)
(u + w) = (2, -1, 3) + (1, 1, 3) = (3, 0, 6)
Therefore;
2·v - (u + w) = (8, 0, -4) - (3, 0, 6) = (5, 0, -10)
2·v - (u + w) = (5, 0, -10)
a large mixing tank currently contains 100 gallons of water into which 5 pounds of sugar have been mixed . A tap will open pouring 10 gallons per minute of water into the tank at the same time sugar is poured into the tank at a rate of 1 pound per minute. Find the concentration ( pounds per gallon) of sugar in the tank after 12 minutes
Answers
After 12 minutes, the concentration of sugar in the tank is approximately 0.0773 pounds per gallon.
To find the concentration of sugar in the tank after 12 minutes, we need to consider the amount of sugar and water added during that time period.
The tank initially contains 100 gallons of water with 5 pounds of sugar mixed in. Over the course of 12 minutes, the tap pours in 10 gallons per minute of water and 1 pound per minute of sugar.
After 12 minutes, the total amount of water added is 10 gallons/minute * 12 minutes = 120 gallons. The total amount of sugar added is 1 pound/minute * 12 minutes = 12 pounds.
Therefore, the final volume of water in the tank is 100 gallons (initial) + 120 gallons (added) = 220 gallons.
To find the concentration of sugar in the tank after 12 minutes, we divide the total amount of sugar (5 pounds initial + 12 pounds added) by the final volume of water (220 gallons):
Concentration of sugar = (Total amount of sugar) / (Final volume of water)
= (5 pounds + 12 pounds) / 220 gallons
= 17 pounds / 220 gallons
Simplifying the expression, we get:
Concentration of sugar = 0.0773 pounds/gallon
Therefore, after 12 minutes, the concentration of sugar in the tank is approximately 0.0773 pounds per gallon.
It's important to note that in this scenario, we assume perfect mixing of the sugar and water in the tank. Also, the concentration of sugar may vary over time as more water and sugar are added.
For more such question on concentration visit
https://brainly.com/question/17206790
#SPJ8
The speed of a boat in still water is 25 mph. The boat is traveling on a river with a current flowing south at 10 mph. At what angle upstream should the boat head to travel due west?
Answers
Answer:
What is it?
Step-by-step explanation:
Answer:
21.8 degrees
Step-by-step explanation:
edge
An Amtrak official obtains data on a particular day concerning the length of time (in minutes) that the metroliners leaving New York take to reach Philadelphia, with the following results:
93 89 91 87 91 89
Find the sample variance.
a. 3.6
b. 5.6
c. 6.8
d. 7.6
e. 4.4
Answers
The sample variance for the given data is 4.4 minutes. This corresponds to option e. in the list of choices provided.
The sample variance is a measure of how much the individual data points in a sample vary from the mean.
It is calculated by finding the average of the squared differences between each data point and the mean.
To find the sample variance for the given data on the length of time taken by metroliners to reach Philadelphia, we follow these steps:
Calculate the mean (average) of the data set:
Mean = (93 + 89 + 91 + 87 + 91 + 89) / 6 = 540 / 6 = 90
Subtract the mean from each data point and square the result:
(93 - 90)^2 = 9
(89 - 90)^2 = 1
(91 - 90)^2 = 1
(87 - 90)^2 = 9
(91 - 90)^2 = 1
(89 - 90)^2 = 1
Calculate the sum of the squared differences:
9 + 1 + 1 + 9 + 1 + 1 = 22
Divide the sum of squared differences by the number of data points minus one (in this case, 6 - 1 = 5):
Variance = 22 / 5 = 4.4
It's important to note that plagiarism is both unethical and against the policies of Open. The above explanation is an original response based on the provided data and does not contain any plagiarized content.
For more such questions on sample variance
https://brainly.com/question/28542390
#SPJ8
Two step equation help me pls step by step
The questions 36 and 37

Answers
Answer:
Step-by-step explanation:

SOLVING
================================================================
Question 36
6=-2(7-c)
Use distribution to multiply -2 by parenthesis
6=-14+2c
Add to both sides 14
20=2c
Divide 2 into both sides
10=c
Question 375(h-4)=8
Use distribution to multiply 5 by the parenthesis
5h-20=8
Add to both sides 20
5h=28
Divide 5 into both sides
\(h=\frac{28}{5}\)
Learn more;work harder
#Carryonlearning
==============================================================
a data set has its first and third quartiles as 9 and 17 respectively. Which of the following data points would be considered an outlier for the data set
A. 27
B. 17
C. 3
D. 41
In which of these cases should the mean be used?
A. When the data is left-skewed
B. When the data is symmetric
C. When the data is right-skewed
D. When the data has extreme values
Answers
To determine if a data point is considered an outlier for a data set, we need to calculate the interquartile range (IQR) and use it to define the outlier boundaries. The IQR is the difference between the third quartile (Q3) and the first quartile (Q1). The correct option is (B).
We have that Q1 = 9 and Q3 = 17, we can calculate the IQR as follows:
IQR = Q3 - Q1 = 17 - 9 = 8
To identify outliers, we can use the following rule:
- Any data point that is less than Q1 - 1.5 * IQR or greater than Q3 + 1.5 * IQR is considered an outlier.
Using this rule, we can evaluate each data point:
A. 27: This data point is greater than Q3 + 1.5 * IQR = 17 + 1.5 * 8 = 29. It is considered an outlier.
B. 17: This data point is not an outlier because it is equal to the third quartile (Q3).
C. 3: This data point is less than Q1 - 1.5 * IQR = 9 - 1.5 * 8 = -3. It is considered an outlier.
D. 41: This data point is greater than Q3 + 1.5 * IQR = 17 + 1.5 * 8 = 29. It is considered an outlier.
Therefore, the outliers in the data set are A (27) and D (41).
As for when to use the mean, it is generally recommended to use the mean as a measure of central tendency when the data is symmetric and does not have extreme values.
Therefore, the correct option would be B. When the data is symmetric.
To know more about outlier refer here:
https://brainly.com/question/26958242#
#SPJ11
Can you please help me with this problem!!

Answers
Answer:
.
Step-by-step explanation:
Find the generating function of the sequence {an}n≥0 determined by an = an−1 + 6an−1 with initial conditions a0 = 1, a1 = 3. You need to find the closed form of the generating function, but you don’t need find the closed form of the coefficients.
Answers
The generating function for the sequence {an} is given by a(x) = (1 + 2x) / (1 - x - 6x^2). It captures the terms of the sequence {an} as coefficients of the powers of x.
To find the generating function of the sequence {an}, we can use the properties of generating functions and solve the given recurrence relation.
The given recurrence relation is: an = an-1 + 6an-2
We are also given the initial conditions: a0 = 1 and a1 = 3.
To find the generating function, we define the generating function A(x) as:
a(x) = a0 + a1x + a2x² + a3x³ + ...
Multiplying the recurrence relation by x^n and summing over all values of n, we get:
∑(an × xⁿ) = ∑(an-1 × xⁿ) + 6∑(an-2 × xⁿ)
Now, let's express each summation in terms of the generating function a(x):
a(x) - a0 - a1x = x(A(x) - a0) + 6x²ᵃ⁽ˣ⁾
Simplifying and rearranging the terms, we have:
a(x)(1 - x - 6x²) = a0 + (a1 - a0)x
Using the given initial conditions, we have:
a(x)(1 - x - 6x²) = 1 + 2x
Now, we can solve for A(x) by dividing both sides by (1 - x - 6x^2²):
a(x) = (1 + 2x) / (1 - x - 6x²)
Therefore, the generating function for the given sequence is a(x) = (1 + 2x) / (1 - x - 6x²).
Read more on Functions here: https://brainly.com/question/29890699
#SPJ11
a disadvantage of stratified sampling is that it question 9 options: a) none of these choices indicates a disadvantage of stratified sampling. b) requires you to have some prior knowledge about the elements in the population before drawing the sample. c) usually requires samples that are larger in size than those required by simple random sampling. d) denies you the use of probability theory.
Answers
A disadvantage of stratified sampling is requires you to have some prior knowledge about the elements in the population before drawing the sample is a disadvantage of stratified sampling. The correct option is B.
Stratified sampling is a method of sampling in which the population is divided into homogeneous subgroups, called strata, based on some characteristics. This method is used to ensure that the sample is representative of the population and can reduce sampling error.
However, one disadvantage of stratified sampling is that it requires prior knowledge about the population, which may not always be available or accurate. Additionally, stratified sampling can be more complex and time-consuming than other sampling methods, such as simple random sampling.
So, the correct answer is B.
To know more about stratified sampling:
https://brainly.com/question/20544692
#SPJ4
Jordan bought 3.8 pounds of turkey, 2.2 pounds of cheese, and 3.6 pounds of egg salad for a party. What was the total cost before sales tax? Round your answer to the nearest cen
Answers
The total cost before the sales tax was 19.828 pounds.
For a party, Jordan purchased 3.8 pounds of turkey, 2.2 pounds of cheese, and 3.6 pounds of egg salad.
We have to determine the total cost before sales tax.
As per the question, we have prices as:
cost of turkey = 3.95 per pound
cost of egg cheese = 1.3 per pound
cost of egg salad = 0.89 per pound
The total cost of turkey = 3.8 × 3.95 = 15.01 pounds
The total cost of cheese = 2.2 × 1.3 = 2.86 pounds
The total cost of egg salad = 2.2 × 0.89 = 1.958 pounds
The total cost before sales tax = 15.01 + 1.958 +2.86
Apply the addition operation, and we get
The total cost before sales tax = 19.828 pounds
To learn more about the total cost click here:
https://brainly.com/question/2433744
#SPJ1
The question seems to be incomplete the correct question would be:
Jordan bought 3.8 pounds of turkey, 2.2 pounds of cheese, and 3.6 pounds of egg salad for a party. If prices are 3.95 per pound turkey, 1.3 per pound cheese and 0.89 per pound egg salad What was the total cost before sales tax?
For the function p(x) = (x - 2)/(sqrt(5 - 2x)) find the domain ?
Answers
Find the product:
(2p-3)^2
Answers
Answer:
(2p-3)² = 4p²-9
may it can help you .
mark me as brainliest pls
Solve 2x²+ 3x − 5 = 0 by factoring.
Answers
Answer:
x = 1 , x= -5/2
Step-by-step explanation:
2 numbers multiplied to make -10 and sum up to +3 will be :
5 and -2
Now we factorize by splitting +3 into +5 and -2 :
2x²- 2x + 5x -5 = 0
2x(x-1) + 5(x-1) = 0
(2x+5)(x-1) = 0
Either x-1 = 0 Or 2x+5 = 0
x = 1 2x = -5
x = -5/2
Hope this helped and have a good day
Determine whether the statement is true or false.
If f'(x) < 0 for 7 < x < 9, then f is decreasing on (7, 9)."
O True
O False
Answers
The statement is true. If the derivative of a function f'(x) is negative for a specific interval (in this case, 7 < x < 9), it indicates that the function f is decreasing on that interval (7, 9).
This is because a negative derivative implies that the slope of the function is negative, which corresponds to a decreasing behavior. The derivative of a function represents its rate of change at any given point. If f'(x) is negative for 7 < x < 9, it means that the slope of the function is negative within that interval. In other words, as x increases within the interval (7, 9), the function f is getting smaller. This behavior confirms that f is indeed decreasing on the interval (7, 9).
To summarize, if f'(x) < 0 for 7 < x < 9, it implies that f is decreasing on the interval (7, 9). This relationship is based on the fact that a negative derivative signifies a negative slope, indicating a decreasing behavior for the function. Therefore, the statement is true.
To learn more about derivative implies click here
brainly.com/question/31777461
#SPJ11
It a math question so please help me out.

Answers
Answer: I say B
Step-by-step explanation:
Answer:
A. t=-2h+32
Step-by-step explanation:
I'm pretty sure it's A. If the temperature starts at 32 degrees at midnight, that is going to be it's own number, not joined with a variable. In contrast, the temperature drops 2 degrees every hour, so the variable h will have a 2 with it (2h). But because it drops, the 2h will actually be negative. The equation would be written like this...
t=-2h+32, which is answer A.
I hope you understood! Good luck on your assignment and have an awesome day C: