Solve for x.
-4x+60 < 72
OR 14z +11 <-31
Answers
The value of x is 3 and -3 respectively.
How to solve the inequalityGiven that;
4x+60 < 72 (1)14x +11 <-31 (2)From equation (1)
4x+60 < 72
First, collect like terms
4x < 72 - 60
subtract like terms
4x < 12
Make 'x' the subject
x < 12/ 4
x < 3
For equation (2)
14x +11 <-31
collect like terms
14x < -31 - 11
14x < -42
Make 'x' the subject
x < -42/ 14
x < -3
Thus. the value of x is 3 and -3 respectively.
Learn more about inequalities here:
https://brainly.com/question/25275758
#SPJ1
Related Questions
WILL MARK BRAINLY FOR WHO EVER ANSWERS THIS RIGHT

Answers
Answer:
B
Step-by-step explanation:
Hope this helps!
Standard Scores
Use both the Student ID and Distance to Work variables.
List the Student ID at TESU in ascending order of Distance to Work.
Calculate the z-scores associated with each student (use the sample standard deviation for this calculation).
Identify potential outliers and explain your reasoning.
Confidence Intervals/Samples
Take a sample of the first four data points for the variable Distance to Work (unsorted - use the original order in the dataset).
Determine the 95% and 99% confidence intervals using the same size of 4.
Describe and compare the two intervals.
Take a sample of the first seven data points for the variable Distance to Work (unsorted - use the original order in the dataset).
Determine the 95% confidence interval. Use the same mean and SD, but change the sample size to 20 and determine the 95% confidence interval.
Describe and compare the two intervals.
STUDENT DATA TABLE
ID School Enrolled Months enrolled Birthday month Distance to Work Height Foot Size Hand Size Sleep Homework
1 Arts and Sciences 12 January 0 60 8 5 360 30
2 Applied Science and Technology 6 February 0 62 7 6 400 45
3 Business and Management 8 April 5 66 10 7 420 60
4 Nursing 10 June 10 68 12 8 440 15
5 Public Service 48 July 15 68 14 8 540 75
6 Arts and Sciences 48 June 30 70 12 9 480 120
7 Applied Science and Technology 36 October 32 72 12 8 320 80
8 Applied Science and Technology 32 November 36 75 14 7 440 60
9 Nursing 6 July 8 63 9 7 300 90
10 Arts and Sciences 22 May 22 80 14 9 420 30
11 Business and Management 15 February 10 65 8 6 500 60
12 Public Service 20 April 4 71 10 8 400 20
13 Applied Science and Technology 11 March 15 66 9 7 440 60
14 Arts and Sciences 18 November 28 64 9 7 300 30
15 Arts and Sciences 29 January 12 72 10 8 360 80
16 Nursing 13 December 6 63 8 6 480 100
17 Business and Management 49 August 0 79 13 9 410 25
18 Applied Science and Technology 16 April 10 74 12 8 430 15
19 Business and Management 24 September 30 66 10 6 330 60
20 Arts and Sciences 8 May 0 65 9 7 480 30
Answers
For the sample size of 20, the 95% confidence interval is (-4.87, 27.16), which is narrower than the previous interval due to the larger sample size.
What is mean?In statistics, mean is a measure of central tendency that represents the average value of a set of numbers. It is calculated by summing up all the numbers in the set and dividing the sum by the total number of values in the set. Mean is also commonly referred to as the arithmetic mean. It is a commonly used statistical measure in many fields including finance, economics, social sciences, and more.
Here,
To calculate the z-scores associated with each student, we first need to calculate the sample mean and standard deviation for the Distance to Work variable:
Sample mean: (0+0+5+10+15+30+32)/7 = 10.71
Sample standard deviation: √(((0-10.71)² + (0-10.71)² + (5-10.71)² + (10-10.71)² + (15-10.71)² + (30-10.71)² + (32-10.71)²)/6) = 10.72
Now we can calculate the z-scores for each student:
Student 1: (0 - 10.71) / 10.72 = -0.94
Student 2: (0 - 10.71) / 10.72 = -0.94
Student 3: (5 - 10.71) / 10.72 = -0.53
Student 4: (10 - 10.71) / 10.72 = -0.07
Student 5: (15 - 10.71) / 10.72 = 0.40
Student 6: (30 - 10.71) / 10.72 = 1.80
Student 7: (32 - 10.71) / 10.72 = 1.98
Student 8: (8 - 10.71) / 10.72 = -0.25
Student 9: (36 - 10.71) / 10.72 = 2.37
Student 10: (9 - 10.71) / 10.72 = -0.16
Student 11: (22 - 10.71) / 10.72 = 1.05
Student 12: (10 - 10.71) / 10.72 = -0.07
Student 13: (15 - 10.71) / 10.72 = 0.40
Student 14: (28 - 10.71) / 10.72 = 1.54
Student 15: (12 - 10.71) / 10.72 = 0.12
Student 16: (6 - 10.71) / 10.72 = -0.44
Student 17: (0 - 10.71) / 10.72 = -0.94
Student 18: (10 - 10.71) / 10.72 = -0.07
Student 19: (30 - 10.71) / 10.72 = 1.80
Student 20: (0 - 10.71) / 10.72 = -0.94
To identify potential outliers, we can look for z-scores that are more than 2 standard deviations away from the mean (i.e., greater than 2 or less than -2). From the list above, we can see that Students 6, 7, 9, and 19 have z-scores greater than 2, indicating that they may be potential outliers.
For the second sample of seven data points (0, 0, 5, 10, 15, 30, 32), the mean is 11.14 and the standard deviation is 12.05. Using a t-distribution with 6 degrees of freedom (n-1), the 95% confidence interval is (-7.54, 29.82).
To know more about mean,
https://brainly.com/question/3116920
#SPJ1
The volume of a cylinder is 637 cm³. If the radius is 3 cm, what is the height
of the cylinder?

Answers
If the radius is 3 cm, the height of the cylinder is approximately 7.06 cm, which is closest to option B, 7 cm. The correct option is B.
The formula for the volume of a cylinder is V = πr²h, where V is the volume, r is the radius, and h is the height.
We are given that the volume of the cylinder is 637 cm³ and the radius is 3 cm. Substituting these values into the formula, we get:
637 = π(3²)h
Simplifying:
637 = 9πh
h = 637 / (9π)
h ≈ 7.06
Thus, the height of the cylinder is approximately 7.06 cm, which is closest to option B, 7 cm.
For more details regarding volume, visit:
https://brainly.com/question/1578538
#SPJ1
4. The length of your rectangular vegetable garden
is 15 times its width. You used 160 ft of fencing to
surround the garden. How much area do you have
for planting?
A. 150 ft2
B. 800 ft2
C. 375 ft2
D. 1600 ft2
Answers
The area of a garden is the amount of space the garden occupies
The area of the garden is (c) 375 ft^2
The given parameters are:
\(L = 15 \times W\) --- Length equals 15 times width
\(Perimeter=160\)
The perimeter of a rectangle is:
\(Perimeter= 2(L + W)\)
Substitute known values
\(160= 2(15 \times W + W)\)
Divide through by 2
\(80= 15 \times W + W\)
\(80= 15W + W\)
\(80= 16W\)
Divide through by 16
\(5= W\)
Rewrite as:
\(W =5\)
The area of a rectangle is:
\(Area = L \times W\)
Substitute \(L = 15 \times W\)
\(Area = 15 \times W \times W\)
Substitute \(W =5\)
\(Area = 15 \times 5 \times 5\)
\(Area = 375\)
Hence, the area of the garden is (c) 375 ft^2
Read more about areas at:
https://brainly.com/question/2077866
Determine the number of zeros of the polynomial function.h(t) = (t − 6)2 − (t + 6)2
Answers
Answer:
Step-by-step explanation:
(t - 6)^2 = t^2 - 12t + 36
(t + 6)^2 = t^2 + 12t +36
(t - 6)^2 - (t + 6) = t^2 - 12t + 36 - (t^2 + 12t + 36)
(t - 6)^2 - (t + 6) = t^2 - 12t + 36 - t^2 - 12t - 36
(t - 6)^2 - (t + 6) = -24t The other 4 terms cancel out.
-24t = 0 Divide by - 24
t = 0
There is one root.
Given a mean of 34 and a standard deviation of 5. Find the following z-scores.
Answers
The z-score for the raw score of 39 is 1.The z-score for the raw score of 30 is -0.8.Z-scores measure the number of standard deviations a raw score is from the mean. A positive z-score indicates a raw score above the mean, while a negative z-score indicates a raw score below the mean.
To find the z-scores, we need to use the formula:
z = (x - μ) / σ
where:
z is the z-score,x is the raw score,μ is the mean, andσ is the standard deviation.
Let's calculate the z-scores for the given mean of 34 and standard deviation of 5.For a raw score of 39:
z = (39 - 34) / 5
z = 5 / 5
z = 1
So, the z-score for the raw score of 39 is 1.For a raw score of 30:
z = (30 - 34) / 5
z = -4 / 5
z = -0.8
The z-score for the raw score of 30 is -0.8.
For such more questions on Standard deviations:
https://brainly.com/question/24298037
#SPJ11
work out the question
23 - 81 =

Answers
The mathematical expression 23 - √81 has a value of 14 when evaluated, mathematically
How to evaluate the expressionGiven the following expression
23 - √81
The expression 23 - √81 involves finding the difference between the number 23 and the square root of 81.
We know that the square root of 81 is 9, so we can simplify the expression to:
23 - √81 = 23 - 9
Evaluate the difference
23 - √81 = 14
Therefore, the value of the expression is 14.
In evaluating expressions like these, it is important to be familiar with basic arithmetic operations and the rules of exponents and radicals.
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
21x² - 2x + 1/2 =0
find the following quadratic equation by factorization method
PLESE SOMEONE HELP
Answers
Step-by-step explanation:
21x²-2x +1/2 = 0
x² - 2x ×21 + 1/2× 21 = 0
Find the vertex of the quadratic function.
ƒ(x) = 2(x−1)² +3
a. (1,3)
b. (2, -1)
c. (-1,3)
d. (2,3)
Answers
hi,
the function is given with it's canonic form.
canonic form is : f(x) = a ( x-α)² + β
α and β are the value of the coordonnates of the vertex.
so here we have : ƒ(x) = 2(x−1)² +3
with α = 1 and β = 3
so vertex is V (1;3)
So yes, answer is A.
T=PV/k, determined P when T=80, V=20 and K= 0.5
Answers
We have the following equation:
\(T=\frac{PV}{k}\)since we need P, we must move k and V to the left hand side as
\(P=\frac{k\cdot T}{V}\)By substituting the given values, we get
\(\begin{gathered} P=\frac{(0.5)(80)}{20} \\ P=\frac{40}{20} \\ P=2 \end{gathered}\)that is, P is equal to 2.
plzz help its so confusing

Answers
espero que sea de tu agrado la tarea que te estoy enviando
soy de peru
brillith2022
You deposit $500 into a savings account that is compounded annually. The function g(x) = 500(1.02)^x can be used to find the amount of money in the savings account after x years.
What is the constant percent rate of change?
O 102%
O 98%
O 1.02%
O 2%
Answers
Answer:
2%
Step-by-step explanation:
The constant percent rate of change for the function g(x) is option (D) 2% is the correct answer.
What is compound interest?Compound interest is the interest you earn on interest. Compound interest is the interest calculated on the principle and the interest accumulated over the previous period.
For the given situation,
The function \(g(x) = 500(1.02)^x -------- (1)\)
Principle = $500
Number of years, T = x
The formula of amount in compound interest is
\(A=p(1+\frac{r}{n} )^{nT}\)
Interest is compounded annually, so n=1
⇒ \(A=p(1+r)^{T} ------ (2)\)
On comparing equation 1 and 2,
⇒ \(1.02=1+r\)
⇒ \(r=1.02-1\)
⇒ \(r=0.02\)
Rate of interest should be in percentage,
⇒ \(0.02(100\%)\)
⇒ \(2\%\)
Hence we can conclude that the constant percent rate of change for the function g(x) is option (D) 2% is the correct answer.
Learn more about compound interest here
https://brainly.com/question/13155407
#SPJ2
Suppose y varies directly with x. When x is 5, y is 15. What is y when x is 12?
Answers
Answer:
y = 36
Step-by-step explanation:
given y varies directly with x then the equation relating them is
y = kx ← k is the constant of variation
to find k use the condition when x = 5 , y = 15
15 = 5k ( divide both sides by 5 )
3 = k
y = 3x ← equation of variation
when x = 12 , then
y = 3 × 12 = 36
a minus b minus a square plus b square
Answers
Answer:
what is the question about which topic
ABCD is a rectangle. Rectangle A B C D is shown. All angles are right angles. The length of A D is 5 and the length of D C is 12. Use the diagram to answer the questions. The length of AB is 12 . The length of BC is 5 . The length of AC is .
Answers
Answer: 13
Step-by-step explanation:
I used Pythagorean theorem to solve this problem. As DC and AD is 12 and 5, you would do 12²+5²= c². 12²= 144 and 5²= 25. 144+25= 169. It doesn't end there. Do the square root of 169 ---> √169=13.
Given that ABCD is a rectangle, if a diagonal line cuts from A to C make a two equal right angled triangles, the hypotenuse which is the length of AC is 13.
What is a rectangle?A rectangle is a 2-dimensional shape with parallel opposite sides equal to each other and four angles are right angles.
What is Pythagorean theorem?Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c = √( a² + b² )
Given the data in the question;
Length AB and DC = 12Length AD and BC = 5Let line AC be the hypotenuse as it cuts the rectangle into two equal right angled triangle.
From Pythagorean theorem.
c = √( a² + b² )
AC = √( AB² + BC² )
AC = √( 12² + 5² )
AC = √( 144 + 15 )
AC = √169
AC = 13
Therefore, given that ABCD is a rectangle, if a diagonal line cuts from A to C make a two equal right angled triangles, the hypotenuse which is the length of AC is 13.
Learn more about Pythagorean theorem here: https://brainly.com/question/343682
#SPJ2

It is January 2020. 3 IL in January 2020. SIB ine, a small manufacturer unhappy with its performance, (i) hires an independent qunt (and therefore, the agent's sales force). and (ii) gets rid of its own salary only sales force. All other contenting the same, how will these changes affect is in 2020 veres 20192 -will increase unit variable cost, and, (ii) will decrease total fixed cost both -will increase unit variable cost both -will decrease total fixed cost -No change in any of the conta -(i) will decrease unit variable cost, and, (ii) will increase total fixed cont
Answers
If SBI hires an independent agent and the agent's sales force after some unhappy performances, it will help him to increase the unit variable cost for the change deployed.
Also, At the same time, he gets rid of its own ' salary own ' sales force will decrease its total fixed cost.
Hence, will increase the unit variable cost and will decrease the total fix cost.
To read more about sales, visit https://brainly.com/question/15375944
#SPJ4
Consider the function f whose graph is shown below
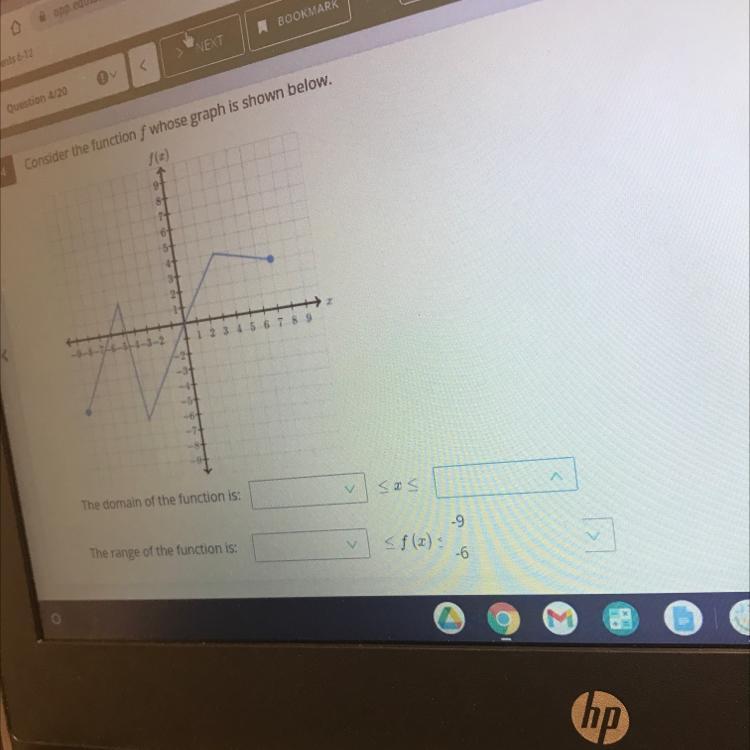
Answers
Answer:
domain - -9 <x < 7
range - -6 < y < 4
Step-by-step explanation:
Find the value of X.

Answers
Answer:
x = 36
Step-by-step explanation:
Given a tangent segment of length 24, and a secant segment from the same point with an external length of 12 and a total length of (12+x), you want to find the value of x.
RelationThe product of lengths from the common point to the two intersections with the circle are the same for both segments. In the case of the tangent, the two intersections with the circle are the same point, so the square of the length is used.
24² = 12(12 +x)
2·24 = 12 +x . . . . . . . divide by 12
36 = x . . . . . . . . . subtract 12
<95141404393>
Mr. Chand is one of the landlords of his town. He buys a land for his daughter spanning over a
area of 480m². He fences the dimensions of the land measuring (x+12) mx (x+16) m. Now he
plans to erect a house with a beautiful garden in the ratio 5:3 respectively. A total of Rs. 5,00,000 is estimated as the budget for the expenses.
1)Give the area of the land purchased in linear polynomial form using algebraic expression
2)Mr. Chand's daughter is ready to share 3/5" of the expenses by her earnings. Express the
fraction in amount.
3)Can you solve the linear equation/polynomial of the area into different factors?
Answers
The required answers are 1) \($$A = x^2 + 28x + 192$$\) 2) 300000 3) \($$x^2 + 28x + 192 = (x + 14 - 2\sqrt{19})(x + 14 + 2\sqrt{19})$$\).
How to deal with area and fractions?area of the land purchased is given as 480m², and the dimensions of the land are (x+12)mx(x+16)m. Therefore, the area of the land can be expressed as:
\($$A = (x+12)(x+16)$$\)
Expanding this expression, we get:
\($$A = x^2 + 28x + 192$$\)
Hence, the area of the land purchased is given by the polynomial expression \($x^2 + 28x + 192$\).
The total budget for the expenses is Rs. 5,00,000. If Mr. Chand's daughter is ready to share 3/5 of the expenses, then the fraction of the expenses she will pay is:
\($\frac{3}{5}=\frac{x}{500000}$$\)
Simplifying this expression, we get:
\($x = \frac{3}{5}\times 500000 = 300000$$\)
Therefore, Mr. Chand's daughter will pay Rs. 3,00,000 towards the expenses.
We can solve the polynomial \($x^2 + 28x + 192$\) into different factors by using the quadratic formula:
\($x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$\)
Here, the coefficients of the polynomial are:
\($$a = 1, \quad b = 28, \quad c = 192$$\)
Substituting these values in the quadratic formula, we get:
\($x = \frac{-28 \pm \sqrt{28^2 - 4\times 1 \times 192}}{2\times 1}$$\)
Simplifying this expression, we get:
\($$x = -14 \pm 2\sqrt{19}$$\)
Therefore, the polynomial \($x^2 + 28x + 192$\) can be factored as:
\($$x^2 + 28x + 192 = (x - (-14 + 2\sqrt{19}))(x - (-14 - 2\sqrt{19}))$$\)
or
\($$x^2 + 28x + 192 = (x + 14 - 2\sqrt{19})(x + 14 + 2\sqrt{19})$$\)
So, we have factored the polynomial into two factors.
To know more about Area visit;
brainly.com/question/22469440
#SPJ1
Which of these has the same value as 45/8? Which of these has the same value as 45/8?
6 5/8
8 5/8
5 5/8
7 5/8
Answers
Answer: 5 5/8
Step-by-step explanation:
6 5/8= 6*8= 48 48+5=53 53/8
8 5/8= 8*8=64 64+5=69 69/8
5 5/8= 5*8=40 40+5=45 45/8
7 5/8= 7*8=56 56+5=61 61/8
The ratio of the number of model cars that Jim owns to the number of model cars Terrence owns is 8 : 6. Terrence owns 36 models cars. How many model cars does Jim own?
Answers
The number of Jim's model car is 48
How to determine the number of JIm's carFrom the question, we have the following parameters that can be used in our computation:
Ratio of the number of model cars that Jim owns to the number of model cars Terrence owns is 8 : 6
This means that
Jim : Terrence = 8 : 6
Also from the question, we have
Terrence owns 36 models cars
This means that
Terrence = 36
Substitute the known values in the above equation, so, we have the following representation
Jim : 36 = 8 : 6
Multiply by 6
Jim : 36 = 48 : 36
So, we have
Jim = 48
Hence, the number of car is 48
Read more about ratio at
https://brainly.com/question/1781657
#SPJ1
The graph of f(x)=2^x is shown in black (k). Match each transformation of this function with a graph below.

Answers
Answer:
Step-by-step explanation:
From the graph attached,
Black curve represents a function f(x) = 2ˣ
When this curve is reflected over the x-axis image of the function will be,
g(x) = -\(2^{x}\) [Red curve]
Similarly, curve represented by h(x) = \(2^{-x}\) is the blue curve [image of f(x) reflected over y-axis]
When this curve is reflected over the x-axis, image of the function will be,
h'(x) = \(-2^{-x}\) [green curve]
\(-2^{x}\) → Red
\(-2^{-x}\) → Green
\(2^{-x}\) → Blue
Point E is drawn on the graph so that line EF is parallel to line CD.
On a coordinate plane, line C D goes through (negative 10, negative 2) and (10, 6). Point F is at (6, negative 4).
If the coordinates of point E are (, y), what is the value of y?
−8
−4
0
8
Answers
The value of y is given as follows:
y = -8.
How to obtain the value of y?When two lines are parallel, we have that they have the same slope.
Given two points, the slope is calculated as the change in y divided by the change in x.
The slope of line CD is given as follows:
m = (6 - (-2))/(10 - (-10))
m = 8/20
m = 0.4.
The slope of line EF is given as follows:
m = (y + 4)/(-4 - 6)
m = -0.1(y + 4).
As the two lines are parallel, the value of y is obtained as follows:
-0.1(y + 4) = 0.4
y + 4 = -4.
y = -8.
Missing InformationThe x-coordinate of E is of -4.
More can be learned about lines at https://brainly.com/question/24808124
#SPJ1
Square PQRS is rotated 180° counterclockwise around the origin.
Which side in the new square corresponds to side SR?

Answers
The side that is equivalent to side SR is side AB.
How to carry out Rotational Transformation?
When rotating a point 180 degrees counterclockwise about the origin, our point A(x, y) becomes A'(-x, -y). Thus, all we do is make both x and y negative.
The coordinates of the original square are;
P(2, 4); Q(5, 5); R(5, 1); S(2, 1)
Now, applying the transformation rule above gives us;
P(-2, -4); Q(-5, -5); R(-5, -1); S(-2, -1)
The side that is therefore equivalent to side SR is side AB.
Read more about Rotational Transformation at; https://brainly.com/question/26249005
#SPJ1
Please i need to find the era bounded by the following curves

Answers
Answer:
10 2/3 or 32/ 3
Step-by-step explanation:
5 - x^2 - (2 - 2x) =
= -x^2 + 2x + 3
Integral of (-x^2 + 2x + 3)dx from -1 to 3 =
= -x^3/3 + 2x^2/2 + 3x from -1 to 3
= -x^3/3 + x^2 + 3x from -1 to 3
= -27/3 + 9 + 9 - (1/3 + 1 - 3)
= -9 + 9 + 9 - 1/3 - 1 + 3
= 11 - 1/3
= 10 2/3 = 32/3
Answer:
32/3
Step-by-step explanation:
Check the pdf :)
if the scale on a map is inches/ miles equal 1/50 find the following actual distance of 2.5 inches and 4.75 inches
Answers
The scale is given inches/ miles equal 1/50. This means that 1 inch is equal to 50 miles.
We can use the rule of three to find the real value.
Then
1 inch --------------------------- 50miles
2.5 inches x
Where x=(2.5inch*50miles)/1 inch
x = 125 miles
For 4.75 inches
1 inch --------------------------- 50miles
4.75 inches--------------------- x
Where x =(4.75 inch*50miles)/1inch
x = 237.5 miles
Which is the largest ratio?
5/36, 2:9, 3 to 18, 1:3
Answers
The largest ratio, among the following ratios: 5/36, 2:9, 3 to 18, 1:3 is 1:3.
How the largest ratio is determined:The ratio refers to the relative size of one quantity compared to another.
The ratio, which is the quotient of two quantities or values, can be expressed as a decimal, percentage, or fraction. We can also express the ratio in its standard form (:).
Given Sum of Equivalent
Ratio Ratios Ratios
5/36 36 13.89% or 0.1389
2:9 11 18.18% or 0.1818
3 to 18 21 14.28% or 0.14.28
1:3 4 25% or 0.25
Thus, we can conclude that 1:3 is the largest ratio amont the others.
Learn more about ratios at https://brainly.com/question/2328454.
#SPJ1
Given the polynomial 9x2y6 − 25x4y8, rewrite as a product of polynomials.
(9xy3 − 25x2y4)(xy3 + x2y4)
(9xy3 − 25x2y4)(xy3 − x2y4)
(3xy3 − 5x2y4)(3xy3 + 5x2y4)
(3xy3 − 5x2y4)(3xy3 − 5x2y4)
Answers
Answer:
Option 3
(3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
Step-by-step explanation:
Factorize polynomials:
Use exponent law:
\(\boxed{\bf a^{m*n}=(a^m)^n} \ & \\\\\boxed{\bf a^m * b^m = (a*b)^m}\)
9x²y⁶ = 3²* x² * y³*² = 3² * x² * (y³)² = (3xy³)²
25x⁴y⁸ = 5² * x²*² * y⁴*² = 5² * (x²)² * (y⁴)² = (5x²y⁴)²
Now use the identity: a² - b² = (a +b) (a -b)
Here, a = 3xy³ & b = 5x²y⁴
9x²y⁶ - 25x⁴y⁸ = 3²x²(y³)² - 5²(x²)² (y⁴)²
= (3xy³)² - (5x²y⁴)²
= (3xy³ + 5x²y⁴) (3xy³ - 5x²y⁴)
What is the surface area of a cone having a slant height equal to 7.25 cm and radius equal to 3.5 cm?
Answers
Answer:
A≈118.2
Step-by-step explanation:
r= Radius= 3.5
l= Slant height= 7.25
A= πrl+πr2= π·3.5·7.25+π·3.52≈118.20242
I have added a screenshot.

Answers
The probability of getting someone who is a woman or a heavy drinker is,
0.546 to three decimal places.
None of the above is the correct option.
What is the probability?The Probability in mathematics is possibility of an event in time. In simple words how many times that incident is happening in any given time interval.
Given:
The table lists the drinking habits of a group of college students.
If a student is chosen at random,
then the probability of getting someone who is a woman or a heavy drinker,
=P(woman) + P(heavy drinker) - P(woman and heavy drinker)
= 216/405 + 13/405 - 8/405
= 221/405
= 0.546 to three decimal places.
Therefore, the probability is 0.546.
To learn more about the probability;
brainly.com/question/11234923
#SPJ1