Answers
Answer:
x > 5
Step-by-step explanation:
there you go! :)

Related Questions
Green's Theorem. For given region R and vector field F;
F =< −3y^2, x^3 + x>; R is the triangle with vertices (0, 0), (1, 0), and (0, 2).
a. Compute the two-dimensional curl of the vector field.
b. Is the vector field conservative?
c. Evaluate both integrals in Green's Theorem and check for consistency.
Answers
a. The two-dimensional curl of the vector field F =\(< -3y^2, x^3 + x >\) is given by curl(F) = \(3x^2 + 1 + 6y\).
b. The vector field F is not conservative because its curl is non-zero.
c. The line integral evaluates to 0, and the double integral evaluates to 7/2. These results are inconsistent, violating Green's Theorem.
a. To compute the two-dimensional curl of the vector field F = <\(-3y^2, x^3 + x >\), we need to find the partial derivatives of the components of F with respect to x and y and take their difference.
Let's start by finding the partial derivative of the first component, -3\(y^2\), with respect to y:
∂(-3\(y^2\))/∂y = -6y.
Now, let's find the partial derivative of the second component, \(x^3\) + x, with respect to x:
∂(\(x^3\)+ x)/∂x = \(3x^2\) + 1.
The two-dimensional curl of the vector field F is given by:
curl(F) = ∂F₂/∂x - ∂F₁/∂y
= \((3x^2 + 1) - (-6y)\)
=\(3x^2 + 1 + 6y.\)
b. To determine if the vector field F is conservative, we need to check if the curl of F is zero (∇ × F = 0). If the curl is zero, then F is conservative; otherwise, it is not conservative.
In this case, the curl of F is:
curl(F) = \(3x^2 + 1 + 6y\).
Since the curl is not zero (it contains both x and y terms), the vector field F is not conservative.
c. Green's Theorem relates the line integral of a vector field around a simple closed curve C to the double integral of the curl of the vector field over the region R enclosed by C.
Green's Theorem can be stated as:
∮C F · dr = ∬R curl(F) · dA,
where ∮C denotes the line integral around the curve C, F is the vector field, dr is the differential vector along the curve C, ∬R denotes the double integral over the region R, curl(F) is the curl of the vector field, and dA is the differential area element in the xy-plane.
For the given vector field F = \(< -3y^2, x^3 + x >\) and the triangle R with vertices (0, 0), (1, 0), and (0, 2), let's compute both integrals in Green's Theorem.
First, let's compute the line integral ∮C F · dr. The curve C is the boundary of the triangle R, consisting of three line segments: (0, 0) to (1, 0), (1, 0) to (0, 2), and (0, 2) to (0, 0).
Line segment 1: (0, 0) to (1, 0):
We parameterize this line segment as r(t) = <t, 0>, where t ranges from 0 to 1.
dr = r'(t) dt = <1, 0> dt,
\(F(r(t)) = F( < t, 0 > ) = < -3(0)^2, t^3 + t > = < 0, t^3 + t > .\)
\(F(r(t)) dr = < 0, t^3 + t > < 1, 0 > dt = 0 dt = 0.\)
Line segment 2: (1, 0) to (0, 2):
We parameterize this line segment as r(t) = <1 - t, 2t>, where t ranges from 0 to 1.
dr = r'(t) dt = <-1, 2> dt,
\(F(r(t)) = F( < 1 - t, 2t > ) = < -3(2t)^2, (1 - t)^3 + (1 - t) > = < -12t^2, (1 - t)^3 + (1 - t) > .\)
\(F(r(t)) dr = < -12t^2, (1 - t)^3 + (1 - t) > < -1, 2 > dt = 14t^2 - 2(1 - t)^3 - 2(1 - t) dt.\)
Line segment 3: (0, 2) to (0, 0):
We parameterize this line segment as r(t) = <0, 2 - 2t>, where t ranges from 0 to 1.
dr = r'(t) dt = <0, -2> dt,
F(r(t)) = \(F( < 0, 2 - 2t > ) = < -3(2 - 2t)^2, 0^3 + 0 > = < -12(2 - 2t)^2, 0 >\).
\(F(r(t)) · dr = < -12(2 - 2t)^2, 0 > < 0, -2 > dt = 0 dt = 0.\)
Now, let's evaluate the double integral ∬R curl(F) · dA. The region R is the triangle with vertices (0, 0), (1, 0), and (0, 2).
To set up the double integral, we need to determine the limits of integration. The triangle R can be defined by the inequalities: 0 ≤ x ≤ 1 and 0 ≤ y ≤ 2 - x.
∬R curl(F) · dA
= ∫[0,1] ∫[0,2-x] (\(3x^2\) + 1 + 6y) dy dx.
Integrating with respect to y first, we have:
∫[0,1] (\(3x^2\) + 1 + 6(2 - x)) dx
= ∫[0,1] (\(3x^2\) + 13 - 6x) dx
=\(x^3 + 13x - 3x^{2/2} - 3x^{2/2 }+ 6x^{2/2\) evaluated from x = 0 to x = 1
= 1 + 13 - 3/2 - 3/2 + 6/2 - 0 - 0 - 0
= 14 - 3 - 3/2
= 7/2.
The line integral ∮C F · dr evaluated to 0, and the double integral ∬R curl(F) · dA evaluated to 7/2. Since both integrals do not match (0 ≠ 7/2), they are inconsistent.
Therefore, Green's Theorem is not satisfied for the given vector field F and the triangle region R.
for such more question on integral
https://brainly.com/question/12231722
#SPJ8
An anthill has a volume of 8792 mm3 of dirt. Its radius is 20 mm. How far does an ant have to crawl to get from the base of the cone to the top of the hill? (This is the
slant height, s, of the cone.) Answer the questions to find out.

Answers
Answer:
The slope is 29 mm.
Step-by-step explanation:
What we know:
The radius of this cone is 20 mm, and the height is 21mm
s = √r^2 + h^2
s = √20^2 + 21^2
s = √400 + 441
s = √841
s = 29 mm
The slant height of the cone is required,
The ant would have to crawl \(29\ \text{mm}\)
Volume of coneV = Volume of cone = \(8792\ \text{mm}^3\)
r = Radius of cone = 20 mm
h = Height
s = Slant height.
Volume of a cone is given by
\(V=\dfrac{1}{3}\pi r^2h\\\Rightarrow h=\dfrac{3V}{\pi r^2}\\\Rightarrow h=\dfrac{3\times 8792}{3.14\times 20^2}\\\Rightarrow h=21\ \text{mm}\)
From Pythagoras theorem we have
\(s=\sqrt{r^2+h^2}\\\Rightarrow s=\sqrt{20^2+21^2}\\\Rightarrow s=29\ \text{mm}\)
Learn more about slant height:
https://brainly.com/question/6613758
Consider the function g(x)=−(x−1)^3−2. Which ordered pair lies on the inverse of the function?
(62,−3)
(−4, 123)
(3, 1)
(3,−6)
Answers
The ordered pair lie on the inverse of the function is (62,−3).
Option A is the correct answer.
What is a function?A function is a relationship between inputs where each input is related to exactly one output.
Example:
f(x) = 2x + 1
f(1) = 2 + 1 = 3
f(2) = 2 x 2 + 1 = 4 + 1 = 5
The outputs of the functions are 3 and 5
The inputs of the function are 1 and 2.
We have,
f(x) = -(x - 1)³ - 2
The inverse of f(x).
y = -(x - 1)³ - 2
interchange x and y and solve for y.
x = -(y - 1)3 - 2
(y - 1)³ = -2 - x
(y - 1)³ = -(2 + x)
Cuberoot on both sides.
y - 1 = ∛-(2 + x)
y = ∛-(2 + x) + 1
Now,
Substitute in the inverse of g(x).
(62, -3) = (x, y)
(−4, 123) = (x, y)
(3, 1) = (x, y)
(3,−6) = (x, y)
So,
y = ∛-(2 + x) + 1
y = ∛-(2 + 62) + 1
∛-1 = -1
y = -1∛64 + 1
y = -1 x 4 + 1
y = -4 + 1
y = -3
So,
(62, -3) ______(1)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 - 4) + 1
∛-1 = -1
y = ∛(-2 + 4) + 1
y = ∛2 + 1
y = 1.26 + 1
y = 2.26
So,
(-4, 2.26) _______(2)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 + 3) + 1
∛-1 = -1
y = -1∛5 + 1
y = -1 x 1.71 + 1
y = -1.71 + 1
y = -0.71
So,
(3, -0.71) _______(3)
And,
y = ∛-(2 + x) + 1
y = ∛-(2 + 3) + 1
∛-1 = -1
y = -1∛5 + 1
y = -1 x 1.71 + 1
y = -1.71 + 1
y = -0.71
So,
(3, -0.71) ______(4)
Thus,
From (1), (2), (3), (4) we see that,
(62, -3) is the solution to the inverse of g(x).
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
Simplify x^2(y^3)^4 / xy^5 = x^a times y^b
Answers
Answer:
xy^7 - x^a y^b = 0
7723 as a fraction what is the answer
Answers
Answer:
7723 as a fraction is 7723/1
Step-by-step explanation:
Please help me with this "Test of Genius" A-78. Need all of the answers...

Answers
Answer:
D
Step-by-step explanation:
PLEASE HELP. Appreciate it
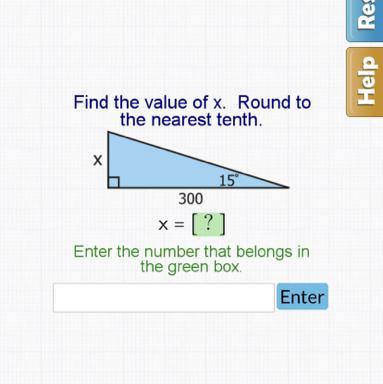
Answers
We can name the sides of a right triangle by finding their location given one of the angles.
The "hypotenuse" is the longest side of a right triangle. It is opposite the right angle.The "opposite" is the side that the angle does not touch.The "adjacent" is the side that the angle does touch, that is not the hypotenuse.The sine, cosine, and tangent ratios are the three basic trigonometric ratios:
The sine ratio: \(\sin\theta=\dfrac{opposite}{hypotenuse}\)The cosine ratio: \(\cos\theta=\dfrac{adjacent}{hypotenuse}\)The tangent ratio: \(\tan\theta=\dfrac{opposite}{adjacent}\)Solving the QuestionThe given angle in this case (\(\theta\)) is the angle that measures 15°.
We're also given the side adjacent to it (that is not the hypotenuse), which measures 300 units.
And finally, we're asked to solve for the side opposite the given angle.
The ratio that involves solving using the opposite and the adjacent sides is the tangent ratio. Plug in all the given values:
\(\tan\theta =\dfrac{opposite}{adjacent}\\\\\tan(15^\circ)=\dfrac{x}{300}\)
Isolate x by multiplying both sides by 300:
\(300\tan(15^\circ)=x\\\\300\tan(15^\circ)=80.4\)
Therefore, x = 80.4 when rounded to the nearest tenth.
Answerx = 80.4
Ava makes $12 per hour plus a
weekly bonus of $10. If her pay this
week was $442, how many hours did
she work? Write and solve the equation.
Answers
12x = 432
x = 36
Ava worked 36 hours this week.
calvin is purchasing dinner for his family. He brought a pizza for $20 and then a salad for each person. The salads cost $4 each. The total bill came to $44. Write and solve an equation that can be used to find s, the number of slads calvin brought.
Answers
The equation would be :
ANSWER:
44=4s+20
The amount of salads he purchased would be:
ANSWER:
6 Salads

the ratio of 36 apples to 18 children
Answers
Answer: 2:1
Step-by-step explanation:
36 to 18 children expressed as a ratio is: 36:18
That can be further reduced by dividing both sides by 18
Which turns into 2:1
7 of 9 The graph shows the speed (m/s) of a car for 40 seconds. By using a single appropriate trapezium, estimate the distance travelled by the car in those 40 seconds. 20 T Speed (m/s) 15 10 LO 5 0 0 5 10 15 20 Time (seconds) 30 35 40 +25
Answers
Therefore , the solution of the given problem of speed comes out to be the average distance travelled is 225 meters.
What exactly is speed?We can determine how fast that anything is traveling by looking at it from a distance. The amount of distance an object can go in a given length of time depends on its speed. Velocity is calculated using the formula velocity = distance/time. The three most used units of speed are meters per second (m/s), kilometers per hour (km/h), and miles per hour (mph) (mph).
Here,
Given :
Time = 40 seconds.
To find the distance:
We use speed and time formula
=> distance = speed * time
=> distance = 15 * 30
=> distance = 225 meters.
Therefore , the solution of the given problem of speed comes out to be the average distance travelled is 225 meters.
To know more about speed , visit
brainly.com/question/2004627
#SPJ1
use the method of variation of parameters to solve the initial value problem x' = ax f(t), x(a) = xa using the following values. 4 -2 16t2 0 1 2t - 40 a= f(t) = x(0) = 2 - 1 4t t 1-2t x(t) =
Answers
The process involves finding the complementary solution x_c(t) by solving the homogeneous equation, determining the particular solution x_p(t) using the method of variation of parameters, and combining them to obtain the general solution x(t).
1. The method of variation of parameters can be used to solve the initial value problem x' = axf(t), x(a) = xa, where a and f(t) are given functions. In this case, we have the values a = 4 - 2t and f(t) = 16t^2. We need to find the solution x(t) using the initial condition x(0) = 2.
2. To solve the initial value problem using the method of variation of parameters, we first find the complementary solution x_c(t) by solving the homogeneous equation x' = ax.
3. For the given a = 4 - 2t, the homogeneous equation becomes x' = (4 - 2t)x. By separation of variables and integration, we find the complementary solution x_c(t) = Ce^(2t - t^2).
4. Next, we find the particular solution x_p(t) by assuming a particular solution of the form x_p(t) = u(t)e^(2t - t^2), where u(t) is a function to be determined.
5. Differentiating x_p(t) and substituting it into the original differential equation, we can solve for u'(t) and determine the form of u(t). After finding u(t), we substitute it back into x_p(t).
6. Finally, the general solution is given by x(t) = x_c(t) + x_p(t). By substituting the values and integrating, we can obtain the specific solution x(t) for the given initial condition.
Learn more about homogeneous equation here: brainly.com/question/12884496
#SPJ11
Fill in the blank. When a data value is converted to a standardized scale representing the number of standard deviations the data value lies from the mean, we call the new value a _____ . When a data value is converted to a standardized scale representing the number of standard deviations the data value lies from the mean, we call the new value a ____.
Answers
When a data value is converted to a standardized scale representing the number of standard deviations the data value lies from the mean, we call the new value a Z-Score.
In statistics, each mathematical formula and each element has an internationally recognised name. This is to ensure that everyone in the world understands what every researcher has to say in every letter. A statistic that tells the number of standard deviations a data value is above or below the mean is called a z-score. And its formula is, Z = (X − μ)/σ
where, μ--> population mean,
σ --> population standard deviation and
x --> the raw-score.
Hence, when a data value is converted to a standardized scale, new value, Z-Score is representing the number of standard deviations the data value lies from the mean.
To learn more about Z-Score, refer:
https://brainly.com/question/25638875
#SPJ4
Please help I will give Brainly

Answers
Answer:
I think it will be B because it is in a linear type
A researcher is interested in the effects of room color (yellow, blue) and room temperature (20, 24, 28 degrees Celsius) on happiness. A total of 120 university students participated in this study, with 20 students randomly assigned to each condition. After sitting for 30 mins. in a room that was painted either yellow or blue, and that was either 20, 24, or 28 degrees, students were asked to rate how happy they felt on a scale of 1 to 15, where 15 represented the most happiness.
The results are as follows:
temperature room color happiness
20 yellow 12
24 yellow 10
28 yellow 6
20 blue 4
24 blue 4
28 blue 4
B) What is the name given to this type of design?
Answers
The name given to this type of design is a factorial design. A factorial design is a design in which researchers investigate the effects of two or more independent variables on a dependent variable.
In this study, two independent variables were used: room color (yellow, blue) and room temperature (20, 24, 28 degrees Celsius), while the dependent variable was happiness.
Each level of each independent variable was tested in conjunction with each level of the other independent variable. There are a total of six experimental conditions (two colors × three temperatures = six conditions), and twenty students were randomly assigned to each of the six conditions.
The researcher then examined how each independent variable and how the interaction of the two independent variables affected the dependent variable (happiness). Therefore, this study is an example of a 2 x 3 factorial design.
To learn more about design: https://brainly.com/question/29829268
#SPJ11
the diamond method product in top and sum on the bottom

Answers
First, list the factors of -36.
-1 , 36
1, -36
-2, 18
2,-18
-3, 12
3,-12
-4,9
4,-9
-6,6
now, find the 2 numbers that added equal -5
-1 + 36 = 35
1 - 36 = -35
-2 + 18 = 16
2+ (-8) = -16
-3 + 12 = 9
3 + (-12) = -9
-4+9 = 5
4+ (-9) = -5
4 and -9
for the function y=-1+6 cos(2 pi/7(x-5)) what is the maximum value
Answers
the maximum value of the function is y = -1 + 6cos(2π/7(26.75-5)) = 5.
The function y = -1 + 6cos(2π/7(x-5)) is a periodic function with a period of 7. The maximum value of the function occurs when the cosine function reaches its maximum value of 1.
So, we need to find the value of x that makes the argument of the cosine function equal to an odd multiple of π/2, which is when the cosine function is equal to 1.
2π/7(x-5) = (2n + 1)π/2, where n is an integer
Simplifying this equation, we get:
x - 5 = (7/4)(2n + 1)
x = 5 + (7/4)(2n + 1)
Since the function has a period of 7, we can restrict our attention to the interval [5, 12].
For n = 0, we get x = 5 + 7/4 = 23/4
For n = 1, we get x = 5 + (7/4)(3) = 26.75
For n = 2, we get x = 5 + (7/4)(5) = 33.25
For n = -1, we get x = 5 + (7/4)(-1) = 1.75
For n = -2, we get x = 5 + (7/4)(-3) = -4.75
Out of these values of x, the only one that lies in the interval [5, 12] is x = 26.75.
To know more about function visit:
brainly.com/question/30721594
#SPJ11
9. Every school day, Mr. Beal asks a randomly selected student to complete a homework problem on the board. If the selected student received a "B" or higher on the last test, the student may use a "pass," and a different student will be selected instead.
Suppose that on one particular day, the following is true of Mr. Beal’s students:
18 of 43 students have completed the homework assignment;
9 students have a pass they can use; and
7 students have a pass and have completed the assignment.
What is the probability that the first student Mr. Beal selects has a pass or has completed the homework assignment? Write your answer in percent.
a. 47% b. 42% c. 52% d. 74%
Answers
The probability that the first student Mr. Beal selects has a pass or has completed the homework assignment is approximately 52%. c.
To find the probability that the first student Mr. Beal selects has a pass or has completed the homework assignment, we need to calculate the probability based on the given information.
Let's define the following events:
A: The selected student has a pass.
B: The selected student has completed the homework assignment.
Given information:
P(A) = 9/43 (probability that a student has a pass)
P(B) = 18/43 (probability that a student has completed the homework assignment)
P(A and B) = 7/43 (probability that a student has a pass and has completed the homework assignment)
We can use the principle of inclusion-exclusion to find the probability of the union of events A and B.
P(A or B) = P(A) + P(B) - P(A and B)
Plugging in the values, we get:
P(A or B) = (9/43) + (18/43) - (7/43)
= 27/43
To express the probability as a percentage, we multiply by 100:
P(A or B) = (27/43) × 100
≈ 62.79
For similar questions on probability
https://brainly.com/question/23417919
#SPJ8
someone please help 5 points.

Answers
Answer:
7.1 I am pretty sure okay cya
Answer:
7.81
Step-by-step explanation:
using distance formula d√(x1 - x2)^2 + (y2 - y1)^2
√(9 - 3)^2 + (7 - 2)^2
√36 + 25
√61 = 7.810
A bakery offers a sale price of $2.85 for 6 muffins. What is the price per dozen?
The price per dozen muffins is $
.
Answers
Have a good day
(Q2) The set of line segments _____ meet the requirements to form a triangle.8 cm4 cm3 cm
Answers
To form a triangle, the set of line segments must satisfy the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. Therefore, we need to check if the given line segments 8 cm, 4 cm, and 3 cm meet this requirement.
We can start by checking if the sum of the two smaller sides (3 cm and 4 cm) is greater than the largest side (8 cm). 3 cm + 4 cm = 7 cm, which is less than 8 cm. Therefore, these three line segments cannot form a triangle.
In general, for a set of line segments to form a triangle, the largest side must be smaller than the sum of the other two sides. In this case, the line segment of 8 cm is too long compared to the other two sides, which makes it impossible to form a triangle.
In conclusion, there are no line segments that meet the requirements to form a triangle with lengths of 8 cm, 4 cm, and 3 cm.
learn more about the inequality theorem here: brainly.com/question/1163433
#SPJ11
what is the procedure for subtracting polynomials: multiply the second expression by 1 and subtract the two expressions. multiply the second expression by -1 and subtract the two expressions. multiply the second expression by -1 and add the two expressions together. multiply the second expression by 1 and add the two expressions together.
Answers
multiply the second expression by 1 and subtract the two expressions. Add the two expressions together after multiplying the second expression by -1.
Subtracting polynomials involves two steps. First, multiply the second expression by 1 and subtract the two expressions. This will cancel out any common terms and leave the difference between the two. Second, multiply the second expression by -1 and add the two expressions together. This will also cancel out any common terms, but will also add any unique terms that were not present in the other expression. Adding the two expressions together leaves the difference between the two polynomials. By following these two steps, one can easily subtract polynomials.
This will also cancel out any common terms, but will also add any unique terms that were not present in the other expression. Adding the two expressions together will result in the difference between the two polynomials, which is the final answer. By following these two steps, one can easily subtract polynomials and arrive at the correct answer.
Learn more about expression here
https://brainly.com/question/14083225
#SPJ4
consider the following vector field f(x, y) = mi nj. f(x, y) = x2i yj (a) show that f is conservative.
Answers
A scalar potential function f(x,y), the vector field f(x,y) = x^2 i + y j is conservative.
To show that the vector field f(x,y) = x^2 i + y j is conservative, we need to find a scalar potential function f(x,y) such that grad f(x,y) = f(x,y).
So, let's first calculate the gradient of a potential function f(x,y):
grad f(x,y) = (∂f/∂x) i + (∂f/∂y) j
Assuming that f(x,y) exists, then f(x,y) = ∫∫ f(x,y) dA, where dA = dx dy, the double integral is taken over some region in the xy-plane, and the order of integration does not matter.
Now, we need to find f(x,y) such that the partial derivatives of f(x,y) with respect to x and y match the components of the vector field:
∂f/∂x = x^2
∂f/∂y = y
Integrating the first equation with respect to x gives:
f(x,y) = (1/3)x^3 + g(y)
where g(y) is a constant of integration that depends only on y.
Taking the partial derivative of f(x,y) with respect to y and comparing it to the y-component of the vector field, we get:
∂f/∂y = g'(y) = y
Integrating this equation with respect to y gives:
g(y) = (1/2)y^2 + C
where C is a constant of integration.
Therefore, the scalar potential function is:
f(x,y) = (1/3)x^3 + (1/2)y^2 + C
where C is an arbitrary constant.
Since we have found a scalar potential function f(x,y), the vector field
f(x,y) = x^2 i + y j is conservative.
Learn more about potential function here
https://brainly.com/question/28156550
#SPJ11
0 Question 32 1 pts Caroline has 6.8 L of lemonade to serve 20 people. How many milliliters can she pour into each glass if she divides the lemonade up evenly among her guests? Question 33 1 pts Provi
Answers
If Caroline has 6.8 L of lemonade to serve 20 people. Caroline can pour 340 milliliters of lemonade into each glass.
To find out how many milliliters of lemonade Caroline can pour into each glass, we need to convert the volume of lemonade from liters to milliliters and then divide it equally among the 20 guests.
1 liter is equal to 1000 milliliters. So, Caroline has 6.8 L * 1000 mL/L = 6800 mL of lemonade.
To divide it equally among 20 guests, we divide the total volume of lemonade by the number of guests:
6800 mL / 20 = 340 mL.
Therefore, Caroline can pour 340 milliliters of lemonade into each glass.
Learn more about volume at https://brainly.com/question/11854151
#SPJ11
What is the Surface Area of the prism, in square centimeters?

Answers
Answer:
\(2( \frac{1}{2} \times 4 \times 6 ) + 2( 5 \times 10 ) + ( 6 \times 10 )\)
\(= {184cm}^{2}\)
fill in the missing value in the given equivalent ratios 5:6=____:42
Answers
Given:
\(5\colon6=x\colon42\)Solve for x,
\(\begin{gathered} \frac{5}{6}=\frac{x}{42} \\ 5\times42=x\times6 \\ 210=6x \\ x=\frac{210}{6} \\ x=35 \end{gathered}\)Answer: x = 35.
Answer: 5:6 = 35:42
Step-by-step explanation:
\(\displaystyle\\5:6=\\\\\frac{5}{6} =\\\\\frac{5(7)}{6(7)}=\\\\\frac{35}{42} =\\\\35:42\)
Determine whether the series is convergent or divergent. 1 1 2 2 1 3 3 1 4 4 1 5 5 ⋯
Answers
Step-by-step explanation:
clearly divergent.
the elements of the series are getting bigger and bigger intercepted by some constant "1" (but they don't help here - after every intercepting "1" are 2 numbers that are larger by 1 than the 2 numbers before the intercepting "1", and that continues into infinity, so, the numbers will go to infinity, and that shows that the series is divergent).
In a hat, you have index cards with the numbers 1 through 10 written on them. Find how many of the 10 possible numbers you can pick match the described event, then drag and drop each of the numbers into the correct box to order the events from least likely to happen (1) to most likely to happen (8) when you pick one card at random.A. You pick a number greater than 0.B. You pick an even number.C. You pick a number that is at least 2.D. You pick a number that is at most 0.E. You pick a number divisible by 3.F. You pick a number divisible by 5.G. You pick a prime number.H. You pick a number less than the greatest prime number among the numbers 1 through 10.
Answers
The order of events from least likely to most likely are as follows:
D. You pick a number that is at most 0A. You pick a number greater than 0C. You pick a number that is at least 2B. You pick an even numberE. You pick a number divisible by 3F. You pick a number divisible by 5G. You pick a prime numberH. You pick a number less than the greatest prime number among the numbers 1 through 10The reason for this order is because of the chances of each event occurring. Event D has the least chance of occurring because no numbers in the set have a value less than or equal to 0. Event A is the next least likely because only one number in the set is greater than 0, which is the number 1. Event C is the next least likely because only two numbers in the set are at least 2 (2 and 3). Event B is the next least likely, as there are only five even numbers in the set (2, 4, 6, 8, and 10). Events E, F, G, and H are the most likely to occur, because of the number of numbers that are divisible by 3, and 5, and are prime numbers.
To learn more about "Least likely events": brainly.com/question/30311304
#SPJ11
Samantha won a trip to Europe in a contest she had entered. Rather than take the trip, she opted to take the cash value of the prize and put it in
savings account she uses as a college fund. She plans to keep this money in the college fund and let it earn interest for 8 years. At the end of
8 years, she'll use the total balance to help pay for tuition at law school

Answers
Answer:
Domain : 0 ≤ x ≤ 8
Range : 5450 ≤ f(x) ≤ 6588.65
Step-by-step explanation:
Expression representing the money Samantha collected after x years is,
f(x) = \(5450(1.024)^{x}\)
Time 'x' duration for the investment starts from t = 0 and ends at 8 years, so the domain of the given function will be,
Range : 0 ≤ x ≤ 8
Money collected in the fund from 0 to 8 years is,
f(0) = \(5450(1.024)^{0}\)
= $5450
f(8) = \(5450(1.024)^{8}\)
= $6588.6
Therefore, range of the graphed function will be,
Range : 5450 ≤ f(x) ≤ 6588.65
The first triangle is dilated to form the second triangle.
What is the scale factor?
4.4 and 1.1
Answers
That can be done by you only as you have attached no diagrams so I have provided the steps below
Dilated means triangles are similarNow take any two sides of triangle (Looking similar)Find ratio of bigger to smaller .Turn into decimalWell done you got the scale factor
