Light travels 9. 45 \cdot 10^{15}9. 45⋅10 15
9, point, 45, dot, 10, start superscript, 15, end superscript meters in a year. There are about 3. 15 \cdot 10^73. 15⋅10 7
3, point, 15, dot, 10, start superscript, 7, end superscript seconds in a year. How far does light travel per second?
Write your answer in scientific notation.
Answers
Light travels at a constant speed of approximately 3 x 10⁸ meters per second in a vacuum, which is also known as the speed of light.
How to find speed of light?The speed of light is a fundamental constant in physics and is denoted by the symbol "c". In a vacuum, such as outer space, light travels at a constant speed of approximately 299,792,458 meters per second, which is equivalent to 3 x 10⁸ meters per second (to three significant figures).
In the question, we were given the distance that light travels in one year (9.45 x 10¹⁵ meters) and the number of seconds in one year (3.15 x 10⁷ seconds). To find how far light travels per second, we simply divided the distance per year by the time per year.
To find how far light travels per second, we need to divide the distance it travels in a year by the number of seconds in a year:
Distance per second = Distance per year / Time per year
Distance per second = 9.45 x 10¹⁵ meters / 3.15 x 10⁷ seconds
Distance per second = 3 x 10⁸ meters per second (approx.)
Therefore, light travels approximately 3 x 10⁸ meters per second, which is also known as the speed of light.
It is worth noting that the speed of light is an extremely important quantity in physics and has many implications for our understanding of the universe. For example, the fact that the speed of light is constant in all reference frames is a key component of Einstein's theory of relativity. Additionally, the speed of light plays a crucial role in astronomy and cosmology, as it allows us to measure the distances between celestial objects and study the behavior of light over vast distances.
Learn more about Speed of light
brainly.com/question/12910903
#SPJ11
Related Questions
3. Look at the averages for all individuals in your group. Was
the hypothesis you stated in the previous question supported by the
"average data"? Explain your answer!!!
Answers
The improper integral ∫ 1/x dx from 0 to ∞ is divergent. The improper integral ∫ 1/x dx from 0 to ∞ represents the integral of the function 1/x with respect to x over the interval from 0 to positive infinity.
To determine whether this integral is convergent or divergent, we need to evaluate it.
Let's split the integral into two parts: from 0 to 1 and from 1 to ∞.
∫(0 to 1) 1/x dx
This part of the integral is a finite integral, and it can be evaluated as:
∫(0 to 1) 1/x dx = [ln|x|] (0 to 1) = ln(1) - ln(0)
However, ln(0) is undefined, so this part of the integral does not converge.
Now let's evaluate the second part of the integral:
∫(1 to ∞) 1/x dx
This integral represents the area under the curve of the function 1/x from 1 to ∞. This is a well-known integral and is known to diverge. As x approaches infinity, the value of 1/x approaches 0, but it never reaches 0. Therefore, the area under the curve keeps increasing indefinitely, and the integral diverges.
Since either part of the integral diverges, the overall integral ∫ 1/x dx from 0 to ∞ is divergent.
Learn more about integral here: https://brainly.com/question/31059545
#SPJ11
3. Given: BAM is a right angle. If mBAM=4x+2, then solve for the value of x.

Answers
Answer:
3. x = 17
4. a. m<NMP = 48°
b. m<NMP = 60°
Step-by-step explanation:
3. Given that <BAM = right angle, and
m<BAM = 4x + 22, set 90° equal to 4x + 22 to find x.
4x + 22 = 90
Subtract 22 from both sides
4x + 22 - 22 = 90 - 22
4x = 68
Divide both sides by 4
4x/4 = 68/4
x = 17
4. a. m<NMQ = right angle (given)
m<PMQ = 42° (given)
m<PMQ + m<NMP = m<NMQ (angle addition postulate)
42 + m<NMP = 90 (substitution)
m<NMP = 90 - 42 (subtracting 42 from each side)
m<NMP = 48°
b. m<NMQ = right angle (given)
m<NMP = 2*m<PMQ
Let m<PMQ = x
m<NMP = 2*x = 2x
2x + x = 90° (Angle addition postulate)
3x = 90
x = 30 (dividing both sides by 3)
m<PMQ = x = 30°
m<NMP = 2*m<PMQ = 2*30
m<NMP = 60°
a + b + c= What when a=8,b=11,c=-13
Answers
Answer:
6
Step-by-step explanation:
brainlyiest
Answer:
six
Step-by-step explanation:
8 plus 11 subyract 13
If a firm's profit is modeled by the following function: Z = - 3x2 +12x + 25, Then the maximum profit is ________ .
Answers
To find the maximum profit, we can look for the vertex of the parabolic function representing the profit.
The given profit function is:
\(Z = -3x^2 + 12x + 25\)
We can see that the coefficient of the \(x^2\) term is negative, which means the parabola opens downwards. This indicates that the vertex of the parabola represents the maximum point.
The x-coordinate of the vertex can be found using the formula:
\(x = \frac{-b}{2a}\)
In our case, a = -3 and b = 12. Plugging these values into the formula, we get:
\(x = \frac{-12}{2 \cdot (-3)}\\\\x = \frac{-12}{-6}\\\\x = 2\)
To find the maximum profit, we substitute the x-coordinate of the vertex into the profit function:
\(Z = -3(2)^2 + 12(2) + 25\\\\Z = -12 + 24 + 25\\\\Z = 37\)
Therefore, the maximum profit is 37.
To know more about Coefficient visit-
brainly.com/question/13431100
#SPJ11
A painter charges a flat fee of $100 and $35 per hour (for up to 8 hours), h, that he spends painting. This relationship can be represented by the function f(h)=100+35h where f(h) represents the total amount the painter charges.

Answers
Answer:
I don't know
Step-by-step explanation:
But the question you asked i think you have add and stuff
. what is the probability of being dealt a. a full-house in standard poker? b. a flush? c. one pair? d. two pair? e. a triple? f. four of a kind?
Answers
The probability of being dealt a. a full-house in standard poker
a. \($P(\text{Full House}) = \frac{13 \cdot 12 \cdot 24}{{52 \choose 5}}$\)
b. \($P(\text{Flush}) = \frac{4 \cdot 13P5}{{52 \choose 5}}$\)
c. \($P(\text{One Pair}) = \frac{13 \cdot 12P3 \cdot 4C2 \cdot 4C1 \cdot 4C1}{{52 \choose 5}}$\)
d. \($P(\text{Two Pair}) = \frac{13P2 \cdot 4C2 \cdot 4C2}{{52 \choose 5}}$\)
e. \($P(\text{Triple}) = \frac{13 \cdot 12P2 \cdot 4C3 \cdot 4C1 \cdot 4C1}{{52 \choose 5}}$\)
f. \($P(\text{Four of a Kind}) = \frac{13 \cdot 12 \cdot 4C4 \cdot 4C1}{{52 \choose 5}}$\)
What is probability?
Probability is a measure of the likelihood or chance that a specific event will occur. It quantifies the uncertainty associated with an event or outcome.
a. To calculate the probability of being dealt a full house in standard poker, we need to determine the number of possible full house hands and divide it by the total number of possible hands.
Number of possible full house hands = (number of ways to choose the rank for the three-of-a-kind) * (number of ways to choose the rank for the pair) * (number of ways to arrange the suits)
Number of ways to choose the rank for the three-of-a-kind = 13
Number of ways to choose the rank for the pair = 12
Number of ways to arrange the suits = \(4C3 * 4C2 = 4 * 6 = 24\)
(choose 3 suits out of 4 for the three-of-a-kind and 2 suits out of 4 for the pair)
Total number of possible hands = \(52C5\)
Probability of being dealt a full house = \(\frac{(number\ of\ possible\ full\ house\ hands)} {(total\ number\ of\ possible\ hands) }\)
= \(\frac {(13 * 12 * 24)} {(52C5)}\)
b. The probability of being dealt a flush can be calculated similarly.
Number of possible flush hands = (number of ways to choose 5 cards of the same suit) * (number of ways to arrange the ranks)
Number of ways to choose 5 cards of the same suit = \(4C1\)
Number of ways to arrange the ranks = \(13P5\)
Probability of being dealt a flush = \(\frac{(number\ of\ possible\ flush\ hands)} {(total\ number\ of\ possible\ hands)}\)
= \(\frac{(4 * 13P5)}{(52C5)}\)
c. The probability of being dealt one pair:
Number of possible one pair hands = (number of ways to choose the rank for the pair) * (number of ways to choose the ranks for the remaining 3 cards) * (number of ways to arrange the suits)
Number of ways to arrange the suits = \(4C2 * 4C1 * 4C1\) (choose 2 suits for the pair and 1 suit each for the remaining cards)
Probability of being dealt one pair = \(\frac{(number\ of\ possible\ one\ pair\ hands)} {(total\ number\ of\ possible\ hands)}\)
\(= \frac{(13 * 12P3 * 4C2 * 4C1 * 4C1)} {(52C5)}\)
d. The probability of being dealt two pair:
Number of ways to choose the ranks for the two pairs = \(13P2\)(permutations of 2 ranks out of 13 ranks)
Number of ways to arrange the suits = \(4C2 * 4C2\) (choose 2 suits for each pair)
Probability of being dealt two pair = \(\frac{(number\ of\ possible\ two\ pair\ hands)}{(total\ number\ of\ possible\ hands)}\)
\(= \frac{(13P2 * 4C2 * 4C2)}{(52C5)}\)
e. The probability of being dealt a triple:
Number of possible triple hands = (number of ways to choose the rank for the triple) * (number of ways to choose the ranks for the remaining 2 cards) * (number of ways to arrange the suits)
Number of ways to arrange the suits = \(4C3 * 4C1 * 4C1\) (choose 3 suits for the triple and 1 suit each for the remaining cards)
Probability of being dealt a triple = \(\frac{(number\ of\ possible\ triple\ hands)} {(total\ number\ of\ possible\ hands)}\)
\(= \frac{(13 * 12P2 * 4C3 * 4C1 * 4C1)} {(52C5)}\)
f. The probability of being dealt four of a kind:
Number of possible four of a kind hands = (number of ways to choose the rank for the four of a kind) * (number of ways to choose the rank for the remaining card) * (number of ways to arrange the suits)
Number of ways to arrange the suits = \(4C4 * 4C1\) (choose all 4 suits for the four of a kind and 1 suit for the remaining card)
Probability of being dealt four of a kind = \(\frac{ (number\ of\ possible\ four\ of\ a\ kind\ hands)} {(total\ number\ of\ possible\ hands)}\)
\(=\frac {(13 * 12 * 4C4 * 4C1)} {(52C5)}\)
You can represent these probabilities in LaTeX format using the following equations:
a. \($P(\text{Full House}) = \frac{13 \cdot 12 \cdot 24}{{52 \choose 5}}$\)
b. \($P(\text{Flush}) = \frac{4 \cdot 13P5}{{52 \choose 5}}$\)
c. \($P(\text{One Pair}) = \frac{13 \cdot 12P3 \cdot 4C2 \cdot 4C1 \cdot 4C1}{{52 \choose 5}}$\)
d. \($P(\text{Two Pair}) = \frac{13P2 \cdot 4C2 \cdot 4C2}{{52 \choose 5}}$\)
e. \($P(\text{Triple}) = \frac{13 \cdot 12P2 \cdot 4C3 \cdot 4C1 \cdot 4C1}{{52 \choose 5}}$\)
f. \($P(\text{Four of a Kind}) = \frac{13 \cdot 12 \cdot 4C4 \cdot 4C1}{{52 \choose 5}}$\)
To learn more about probability visit:
https://brainly.com/question/25839839
#SPJ4
A florist uses 5 red roses for every 2 white roses in her bouquets write the ratio of red roses to the total number of flowers in three different ways.
Answers
Answer: 5:7, 5 to 7, 5/7
Step-by-step explanation:
Since the ratio is the number of red roses to total, you must add 5 and 2 to get the total. The ratio is 5 to 7.
These are three ways to write a ratio:
1. Using the colon symbol
5:7
2. Using the word to
5 to 7
3. As a fraction
5/7
Prove each of the following statements using mathematical induction. (a) Prove that for any positive integer n, sigma_j=1^m j^3 = (n(n+1/2)^2 (b) Prove that for any positive integer n, sigma_j=1^n j moddot 2^j = (n - 1)2^n+1 + 2 (c) Prove that for any positive integer n, sigma_j=1^n j (j - 1) = n(n^2 - 1)/3
Answers
(a) Using mathematical induction, we can prove that for any positive integer n, the sum of the cubes of the first n positive integers is equal to (n(n+1)/2)^2.(b) Similarly, by mathematical induction, we can prove that for any positive integer n, the sum of j*(2^j) for j = 1 to n is equal to (n - 1)2^n+1 + 2.(c) By applying mathematical induction, it can be shown that for any positive integer n, the sum of j*(j - 1) for j = 1 to n is equal to n(n^2 - 1)/3.
(a) To prove the statement using mathematical induction, we start by establishing the base case.
For n = 1, the left-hand side (LHS) is 1^3 = 1, and the right-hand side (RHS) is \((1(1+1)/2)^2 = (1/2)^2 = 1/4\). Since LHS = RHS, the statement holds true for n = 1.
Next, we assume that the statement is true for some positive integer k, i.e., \(sigma_j=1^k j^3 = k(k+1)/2^2\). We need to show that it holds for n = k + 1.
Using the assumption, \(sigma_j=1^k j^3 = k(k+1)/2^2\). Adding \((k+1)^3\) to both sides gives \(sigma_j=1^{(k+1)} j^3 = k(k+1)/2^2 + (k+1)^3\). Simplifying the RHS, we get \((k^3 + 3k^2 + 2k + 2) / 4\).
Rearranging the terms and factoring, the RHS becomes\(((k+1)(k+2)/2)^2\). Therefore, we have established that the statement holds for n = k + 1.
By mathematical induction, we conclude that the statement \(sigma_j=1^m j^3 = (n(n+1)/2)^2\)holds for any positive integer n.
The proofs for parts (b) and (c) are similar and can be done by following the same steps of base case verification and the induction assumption, and then deriving the result for n = k + 1.
To know more about mathematical induction refer here:
https://brainly.com/question/30577446#
#SPJ11
An item has a listed price of $95. If the sales tax rate is 3% ,how much is the sales tax (in dollars )
Answers
Answer:
2.85
you multiply the price by the rate translated to a decimal
so
95*.03
=
2.85
Plz Help .............

Answers
\(363.9ft^{2}\)
Step-by-step explanation:
\(Area =\pi r^{2} -\frac{1}{3}\pi r^{2} +\frac{1}{2}r^{2}sin\alpha \\\\\\ = \frac{2}{3}\pi 12^{2} +\frac{1}{2}12^{2}sin120 =363.9ft^{2}\)
Answer:
363.9 ft²
Step-by-step explanation:
The required area is the area of the circle - shaded area
area of circle = πr² = π × 12² = 144π ft²
shaded area = area of sector - area of Δ NBW
area of sector = πr² × \(\frac{120}{360}\) = 144π × \(\frac{1}{3}\) = 48π
area of Δ = \(\frac{1}{2}\) × 12 × 12 × sin120° = 72 × sin120° ≈ 62.35 ft²
Then
shaded area = 48π - 62.35 ≈ 88.45 ft²
area not shaded = 144π - 88.45 ≈ 363.9 ft²
Estimate the intercepts of the graph of the function.

Answers
The y-intercept of the graph is -4 and the x-intercept is (4,-1).
What is an intercept?A y-intercept, also known as a vertical intercept, is the location where the graph of a function or relation intersects the coordinate system's y-axis.
This is done in analytic geometry using the common convention that the horizontal axis represents the variable x and the vertical axis the variable y.
The given equation is y = x² - 3x - 4. The y-intercept is calculated by putting x= 0 in the equation and the x-intercept by putting y = 0.
y-intercept:-
y = x² - 3x - 4
y = 0 - 0 - 4
y = -4
x-intercept:-
y = x² - 3x - 4
x² - 3x - 4 = 0
x² - 4x + x - 4 = 0
x ( x - 4 ) + 1 ( x - 4 ) = 0
( x - 4 ) ( x + 1) = 0
x = 4, -1
Therefore, the y-intercept of the graph is -4 and the x-intercept is (4,-1).
To know more about an intercept follow
https://brainly.com/question/24990033
#SPJ1
an agent gets a commission of Rs 500 on the sales which amount to Rs 5000 how much will the businessman get from the sales
Answers
Step-by-step explanation:
Since commission the commission and is already given then the total sales the businessman gets;Total sales
Rs 5000- Rs 500= Rs 4500
The required amount received by the businessmen is 4500, from the sale.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Let the money businessman get be x,
According to the question,
x + commission of the agent = 5000
x + 500 = 5000
x = 4500
Thus, the required amount received by the businessmen is 4500.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ2
What are the coordinates of point P on the directed line segment from A to B such that P is One-fourth the length of the line segment from A to B?
Answers
Answer:
The answer is explained below
Step-by-step explanation:
The location of point A = (-5, -1) and point B = (4, 1).
To find the coordinate of the point that divides a line segment PQ with point P at \((x_1,y_1)\) and point Q at \((x_2,y_2)\) in the proportion a:b, we use the formula for the x and y coordinates:
\(x-coordinate:\\\frac{a}{a+b}(x_2-x_1)+x_1 \\\\While \ for\ y-coordinate:\\\frac{a}{a+b}(y_2-y_1)+y_1\)
P is One-fourth the length of the line segment from A to B, Therefore AB is divided in the ratio 1:4. The location of point A = (-5, -1) and point B = (4, 1).Therefore:
\(x-coordinate:\\\frac{1}{1+3}(4-(-5))+(-5)=\frac{1}{4}(9)-5=-\frac{11}{4} \\\\While \ for\ y-coordinate:\\\frac{1}{1+3}(1-(-1))+(-1)=\frac{1}{4}(2)-1=\frac{-1}{2}\)
Therefore the coordinate of P is (-11/4, -1/2)
Answer:
the coordinate of P is (-11/4, -1/2)
x= -11/4
y= -1/2
c on edu
Step-by-step explanation:
edu 2021
Help ASAP pls giving brainliest

Answers
Q1: 12.5
Q3: 16
IQR ( Q3-Q1) : 3.5
(100 Points) Given f of x is equal to 10 divided by the quantity x squared minus 7x minus 30, which of the following is true?
f(x) is negative for all x < –3
f(x) is negative for all x > –3
f(x) is positive for all x < 10
f(x) is positive for all x > 10
Answers
Answer:
f(x) is positive for all x > 10
Step-by-step explanation:
Given function:
\(f(x)=\dfrac{10}{x^2-7x-30}\)
Asymptote
Asymptote: a line which the curve gets infinitely close to, but never touches.
Factor the denominator of the function to find the vertical asymptotes:
\(\implies x^2-7x-30\)
\(\implies x^2-10x+3x-30\)
\(\implies x(x-10)+3(x-10)\)
\(\implies (x+3)(x-10)\)
Therefore:
\(f(x)=\dfrac{10}{(x+3)(x-10)}\)
The function is undefined when the denominator is equal to zero.
Therefore, there are vertical asymptotes at x = -3 and x = 10
and a horizontal asymptote at y = 0
f(x) is positive for (10, ∞)
f(x) is negative for (-3, 10)
f(x) is positive for (-∞, -3)

\(\\ \rm\Rrightarrow y=\dfrac{10}{x^2-7x-10}\)
If we factor
\(\\ \rm\Rrightarrow y=\dfrac{10}{(x+3)(x-10)}\)
Horizontal Asymptotes
y=0 as there is no variable in numbersVertical asymptotes
solve the denominator for 0
x=-3x=10Henec option D is correct
For each of the following families of sets, construct the associated bipartite graph. If possible, find a system of distinct representatives. If there is no such system, explain why. (i) A₁ = {1,2,3}, A2 = {2, 3, 4}, A3 = {1}. (ii) A₁ = {1, 2, 3, 4, 5}, A₂ = {1,3}, A3 = {1,3}, A₁ = {1, 2, 3, 4, 5}, A5 = {1,3}.
Answers
(i) The bipartite graph for A₁ = {1,2,3}, A₂ = {2, 3, 4}, A₃ = {1} has a system of distinct representatives.
(ii) The bipartite graph for A₁ = {1, 2, 3, 4, 5}, A₂ = {1,3}, A₃ = {1,3}, A₄ = {1, 2, 3, 4, 5}, A₅ = {1,3} does not have a system of distinct representatives.
To construct the associated bipartite graph for each family of sets, we can represent the sets as vertices and draw edges between them based on their intersection.
(i) Family of sets: A₁ = {1,2,3}, A₂ = {2, 3, 4}, A₃ = {1}
The bipartite graph for this family of sets would have two sets of vertices, one representing the sets A₁, A₂, A₃ and the other representing the elements 1, 2, 3, 4.
The vertices for sets A₁, A₂, A₃ would be connected to the vertices representing the elements that are contained in those sets. The edges would be drawn based on the intersection of the sets.
To find a system of distinct representatives, we need to find a matching where each vertex on the left side (sets) is connected to a unique vertex on the right side (elements). In this case, a system of distinct representatives exists since every set has at least one unique element.
(ii) Family of sets: A₁ = {1, 2, 3, 4, 5}, A₂ = {1,3}, A₃ = {1,3}, A₄ = {1, 2, 3, 4, 5}, A₅ = {1,3}
The bipartite graph for this family of sets would have two sets of vertices, one representing the sets A₁, A₂, A₃, A₄, A₅ and the other representing the elements 1, 2, 3, 4, 5.
The vertices for sets A₁, A₂, A₃, A₄, A₅ would be connected to the vertices representing the elements that are contained in those sets.
To find a system of distinct representatives, we need to find a matching where each vertex on the left side (sets) is connected to a unique vertex on the right side (elements). In this case, a system of distinct representatives does not exist because element 1 is shared by all the sets A₁, A₂, A₃, A₄, A₅, violating the requirement of distinctness.
Learn more about bipartite graphs at
https://brainly.com/question/28062985
#SPJ4

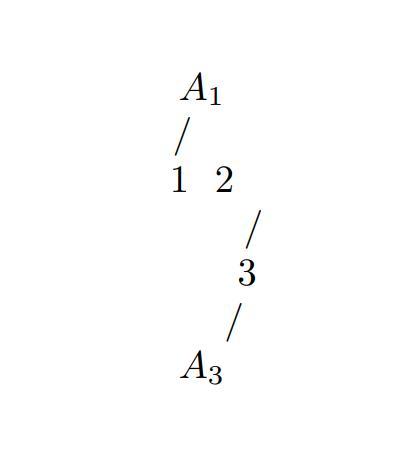
According to a survey conducted by the Texas Free Press, 125 out of 500 people do not have internet access at their homes. What percent of the people surveyed do have internet access at their homes?
Answers
500-125 is 375
375/500 gives 3/4 which is .75
move the decimal over to the right twice to get 75%
125 do not
375 have
500 is the total
500-125 =375
375/500
500 divided by 375 = 0.75
75%
Who does Plato for money ?
Answers
Answer:
what are you talking about the picture is not there
Step-by-step explanation:
Answer:
i ate plato for money if thats what your asking
Step-by-step explanation:
a light year is defined as 5.88 times 10^12 miles: the distance that light travels in 1 year. How far will light travel in 3 years?
Answers
The distance that light will travel in 3 years, given the speed it travels in one year is
How to find the speed travelled ?The notion of a Light Year allows us to quantity the distance that light travels in an entire year. This has allowed scientists to quantify with more ease, the distance to other galaxies and planets.
The distance that light travels in a year is 5. 88 x 10¹² miles.
In 3 years therefore, the distance would be:
= 3 x ( 5.88 x 10 ¹²)
= 17.64 x 10 ¹² miles
Find out more on light years at https://brainly.com/question/23579861
#SPJ1
help me don't worry about the work

Answers
The surface area of the sphere of radius of 7cm is 616 square centimeters.
How to find the approximate surface area?We know that the surface area of a sphere of radius r is given by the formula:
S = 4*(22/7)*r²
Here we want to find the surface area of a sphere whose radius is r = 7 cm.
Replacing it in the formula above, we will get:
S = 4*(22/7)*7²
S = 4*22*7
S = 616
And the units are square centimeters, so the correct option is C.
Learn more about surface area at.
https://brainly.com/question/16519513
#SPJ1
What is 2 4/7 of 10 1/9
Answers
Answer:
from the calculator i got 25.59375
Step-by-step explanation:
solve for x Express your answer as an integers or in simplest radical form 1-x^3=9
Answers
Answer:
\(\large\boxed{\tt x = 2}\)
Step-by-step explanation:
\(\textsf{We are asked to solve for x in the given equation.}\)
\(\textsf{We should know that x is cubed, meaning that it's multiplied by itself 3 times.}\)
\(\textsf{We should isolate x on the left side of the equation, then find x by cubic rooting}\)
\(\textsf{both sides of the equation.}\)
\(\large\underline{\textsf{How is this possible?}}\)
\(\textsf{To isolate variables, we use Properties of Equality to prove that expressions}\)
\(\textsf{are still equal once a constant has changed both sides of the equation. A Cubic}\)
\(\textsf{Root is exactly like a square root, but it's square rooting the term twice instead}\)
\(\textsf{of once.}\)
\(\large\underline{\textsf{For our problem;}}\)
\(\textsf{We should use the Subtraction Property of Equality to isolate x, then cubic root}\)
\(\textsf{both sides of the equation.}\)
\(\large\underline{\textsf{Solving;}}\)
\(\textsf{Subtract 1 from both sides of the equation keeping in mind the Subtraction}\)
\(\textsf{Property of Equality;}/tex]
\(\tt \not{1} - \not{1} - x^{3} = 9 - 1\)
\(\tt - x^{3} = 8\)
\(\textsf{Because x}^{3} \ \textsf{is negative, we should exponentiate both sides of the equation by}\)
\(\textsf{the reciprocal of 3, which is} \ \tt \frac{1}{3} .\)
\(\tt (- x^{3})^{\frac{1}{3}} = 8^{\frac{1}{3}}\)
\(\underline{\textsf{Evaluate;}}\)
\(\tt (- x^{3})^{\frac{1}{3}} \rightarrow -x^{3 \times \frac{1}{3} } \rightarrow \boxed{\tt -x}\)
\(\textsf{*Note;}\)
\(\boxed{\tt A^{\frac{1}{C}} = \sqrt[\tt C]{\tt A}}\)
\(\tt 8^{\frac{1}{3}} \rightarrow \sqrt[3]{8} \rightarrow 2^{1} \rightarrow \boxed{\tt 2}\)
\(\underline{\textsf{We should have;}}\)
\(\tt -x=2\)
\(\textsf{Use the Division Property of Equality to divide each side of the equation by -1;}\)
\(\large\boxed{\tt x = 2}\)
3 friends ordered 2 pizzas of 6 slices each and ate equal amounts, how many slices did each person eat?
A 1
B 2
C 3
D 4
Answers
Answer:
Option D, 4
Step-by-step explanation:
2 pizzas x 6 slices per pizza = 12 slices of pizza
12 slices of pizza divided by 3 friends eating equal slices = 4 slices per friend
Option D, 4, is your answer
A theater has 1,464 seats. The seats are arranged into 62 equal-sized "regular" sections plus one "premium" front-row section. How many seats are in a regular section? How many seats are in the premium front-row section? Explain.
Answers
In the theater, that have 1,464 seats.
1426 seats are in "regular" sections
38 seats are "premium" front-row section
How to find the number of seats in the "regular" sectionsThe seat arrangement is solved by division. In this case the 62 equal spaced is the divisor while the number of seats is the in each row is the quotient
The division is as follows
1464 / 62
= 23 19/31
The number of seats in the regular section is 23 * 62 = 1426
The remainder will be arranged in premium front row
using equivalent fractions
19 / 31 = 38 / 62
the remainder is 38 and this is the seat for the premium front row section
OR 1464 - 1426 = 38 seats
Learn more about division here:
https://brainly.com/question/29401139
#SPJ1
What is 164.362 rounded to 4, 3 and 1 significant figures
Answers
Answer:
4 sigfig is 164.4
3 sigfig is 164.
1 sigfig is 200
hope that answers your question
comment for more explanation
Nico earns $12.50 as a math tutor. Write an equation of this proportional relationship. Your answer should be in the form of y=kx
Answers
Answer:
y=12.50x
Step by step explantion:
Please help me pleasee answer this correctly

Answers
Answer:
(a) center = (0, 0)
(b) vertices = (0, ±3)
(c) co-vertices = (±2, 0)
(d) foci = (0, ±√5)
(e) major axis = 6 units
(f) minor axis = 4 units
(g) LR = 8/3 units
Step-by-step explanation:
\(\boxed{\begin{minipage}{6 cm}\underline{General equation of an ellipse}\\\\$\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center\\\end{minipage}}\)
Given equation:
\(9x^2+4y^2=36\)
Divide both sides of the equation by 36 to rewrite the given equation in the general equation of an ellipse (so that the right side of the equation is 1):
\(\implies \dfrac{9x^2}{36}+\dfrac{4y^2}{36}=\dfrac{36}{36}\)
\(\implies \dfrac{\diagup\!\!\!\!9x^2}{4 \cdot \diagup\!\!\!\!9}+\dfrac{\diagup\!\!\!\!4y^2}{\diagup\!\!\!\!4 \cdot 9}=1\)
\(\implies \dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)
Comparing the equation with the general equation, we can say that:
h = 0k = 0a² = 4 ⇒ a = 2b² = 9 ⇒ b = 3Therefore, the center (h, k) of the ellipse is (0, 0).
As b > a, the ellipse is vertical. Therefore:
b is the major radius and 2b is the major axis.a is the minor radius and 2a is the minor axis.Vertices = (h, k±b)Co-vertices = (h±a, k)Foci = (k, h±c) where c² = b² - a²To find the vertices, substitute the value of b into the formula for the vertices:
\(\begin{aligned} \implies (h, k \pm b)&=(0, 0\pm 3)\\&=(0, \pm3)\end{aligned}\)
Therefore, the vertices are (0, ±3).
To find the co-vertices, substitute the value of a into the formula for the co-vertices:
\(\begin{aligned} \implies (h \pm a, k)&=(0 \pm 2, 0)\\&=(\pm 2,0)\end{aligned}\)
Therefore, the co-vertices are (±2, 0).
To find the value of c, substitute the found values of a and b into c² = b² - a²:
\(\begin{aligned}\implies c^2&=b^2-a^2\\c^2&=3^2-2^2\\c^2&=9-4\\c^2&=5\\c&=\sqrt{5}\end{aligned}\)
To find the foci, substitute the value of c into the formula for the foci:
\(\begin{aligned} \implies (k, h \pm c)&=(0, 0\pm \sqrt{5})\\&=(0, \pm \sqrt{5})\end{aligned}\)
Therefore, the foci are (0, ±√5).
The major axis is 2b:
\(\implies 2b=2(3)=6\;\sf units\)
The minor axis is 2a:
\(\implies 2a=2(2)=4\;\sf units\)
The latus rectum (LR) of an ellipse is a line drawn perpendicular to the its major axis that passes through the foci.
The formula for the endpoints of the latus rectum of a vertical ellipse is:
\(\left(h\pm\dfrac{a^2}{b}, k\pm c \right)\)
Therefore, substituting the values of h, k, a, b and c into the formula, the coordinates of the latera recta are:
\(\implies \left(0\pm\dfrac{2^2}{3}, 0\pm \sqrt{5}\right)\)
\(\implies \left(\pm\dfrac{4}{3}, \pm \sqrt{5}\right)\)
To calculate the length of the latus rectum, subtract the negative x-value from the positive x-value of the endpoints:
\(\implies \dfrac{4}{3}-\left(-\dfrac{4}{3}\right)=\dfrac{8}{3}\; \sf units\)
Therefore, the length of the latus rectum is 8/3 units.

Determine whether each ordered pair is a solution or not a solution to this system of inequalities.
y< −x
2x+y>2
Answers
The ordered pair that is the solution of the given system of inequalities is (2, -2)
What is inequality?A relationship between two expressions or values that are not equal to each other is called inequality.
Given is a system of inequalities, y < -x and 2x+y > 2, we need to determine solution set of the given system of inequalities,
The inequalities are,
y < -x....(i)
2x+y > 2
y < 2-2x...(ii)
To find the ordered pair, put y = -x in equation Eq(ii) and replace < by =
-x = 2 - 2x
x = 2
y = -2
Therefore, the ordered pair, is (2, -2) {look at the graph attached}
Hence, the ordered pair that is the solution of the given system of inequalities is (2, -2)
Learn more about inequalities, click;
https://brainly.com/question/30228778
#SPJ1

The point (3, 5) is reflected across the y-axis.
What are the coordinates of the image of the point?
and 2.
The point (2, -7) is reflected across the x-axis.
What are the coordinates of the image of the point?
Answers
Find an equation of the tangent plane to the given parametric surface at the specified point.r(u, v) = u2 i 8u sin(v) j u cos(v) k; u = 1, v = 0
Answers
The equation of tangent plane is -x + 2x - 1 = 0
Given,
r = < u² , 8usinv , ucosv >
Here,
r = < u² , 8usinv , ucosv >
Differentiate partially with respect to u and v,
\(r_{u}\) = < 2u , 8sinv , cosv >
\(r_{v}\) = < 0, 8ucosv , -4sinv >
Substitute u = 1 and v = 0
\(r_{u}\) = < 2, 0 , 0 >
\(r_{v}\) = < 0 , 8 , 0 >
Now,
N = \(r_{u}\) × \(r_{v}\)
N = \(\left[\begin{array}{ccc}i&j&k\\2&0&1\\0&8&0\end{array}\right]\)
N = -8i -j(0) +16k
N = < -8 , 0 , 16 >
Tangent plane
-8x + 16z + d = 0
Coordinates of tangent plane : <1, 0 ,1>
Substitute the values in the equation,
-8(1) + 16 (1) + d = 0
d = -8
Substitute in the tangent plane equation,
-8x + 16z - 8 = 0
-x + 2x - 1 = 0
Thus equation of tangent plane: -x + 2x - 1 = 0
Know more about tangent plane,
https://brainly.com/question/33705648
#SPJ4