Answers
Answer:
The most logical answer would be C.
Step-by-step explanation:
Related Questions
A plastic pool gets filled up with 10L of water per hour.
a) After 2 hours how much water is in the pool? Write an equation.
b) After how many hours will the pool be 80L?
c) Is part b) linear or nonlinear?
Answers
a) The amount of water in the pool after 2 hours can be calculated using the equation.
Water in pool = 10L/hour × 2 hours = 20L.
b) The pool will be 80L when the equation is satisfied: 80L = 10L/hour × Time.
Solving for Time, we find Time = 8 hours.
c) Part b) is linear.
a) To calculate the amount of water in the pool after 2 hours, we can use the equation:
Water in pool = Water filling rate × Time
Since the pool gets filled up with 10L of water per hour, we can substitute the values:
Water in pool = 10 L/hour × 2 hours = 20L
Therefore, after 2 hours, there will be 20 liters of water in the pool.
b) To determine the number of hours it takes for the pool to reach 80 liters, we can set up the equation:
Water in pool = Water filling rate × Time
We want the water in the pool to be 80 liters, so the equation becomes:
80L = 10 L/hour × Time
Dividing both sides by 10 L/hour, we get:
Time = 80L / 10 L/hour = 8 hours
Therefore, it will take 8 hours for the pool to contain 80 liters of water.
c) Part b) is linear.
The equation Water in pool = Water filling rate × Time represents a linear relationship because the amount of water in the pool increases linearly with respect to time.
Each hour, the pool fills up with a constant rate of 10 liters, leading to a proportional increase in the total volume of water in the pool.
For similar question on amount.
https://brainly.com/question/25720319
#SPJ8
Simplify this problem. |3r−15| if r<5
Answers
Answer:
We have the problem:
|3r−15| if r<5
First we see the equality, if r = 5 we have:
I3r - 15I = I3*5 - 15I = I0I = 0.
Then the only restriction that we have is:
I3r - 15I > 0.
now, we could simplify it a bit further:
if r < 5, then the thing inside the absolute value will always be negative:
Then we can write:
I3*r - 15I = -(3*r -15) > 0
multiplying by -1 in both sides
(3r - 15) < 0.
if we keep simplifying this, we will get our initial restriction:
3r - 15 < 0
3r < 15
r < 15/3 = 5
r < 5
help me out? thank you so much whoever does :))

Answers
Answer:
\(86\)
Step-by-step explanation:
The remaining part forms 360. so
\(233 + 41 + x = 360\)
\(274 + x = 360\)
\(x = 86\)
Answer:
if you’re looking for b,
B = 86
sorry if wrong
waiting times to receive food after placing an order at the local subway follow an exponential distribution with a mean of 60 seconds. what is the probability a customer waits less than 30 seconds?
Answers
It is discovered that there is a 0.3934, or 39.34%. likelihood that a customer waits fewer than 30 seconds using the exponential distribution.
Define the term exponential distribution?The exponential distribution is a mathematical distribution used in test statistic that frequently addresses the amount of time until a given event occurs. Events occur continually, independently, and at a steady average pace during this process.The following equation describes an exponential probability distribution with mean m:
f(x) = μe∧(- μe)
The decay parameter is in the following:
μ = 1/m
When x is less than or equal to a, the probability is given by:
P(X ≤ x) = ∫ f(x) dx (limits 0 → a)\
which can be resolved as follows:
P(X ≤ x) = 1 - e∧(- μe)
Since 60 seconds is the mean in this problem, then decay parameter is:
μ = 1/60
The likelihood that a customer will wait under 39 seconds is:
P(X ≤ 30) = 1 - e∧(- 30/60)
P(X ≤ 30) = 0.3934
Thus, the probability that a consumer will wait less than 30 seconds is 0.3934, or 39.34%.
To know more about the exponential distribution, here
https://brainly.com/question/22692312
#SPJ4
Al released his balloon from the 10-yard line, and it landed at the 16-yard line. If the ball reached a height of 27 yards, what equation represents the path of his toss?
Answers
The equation of the path of the parabola is y = a(x - 13)² + 27
Given data ,
To represent the path of Al's toss, we can assume that the path is a parabolic trajectory.
The equation of a parabola in vertex form is given by:
y = a(x - h)² + k
where (h, k) represents the vertex of the parabola
Now , the balloon was released from the 10-yard line and landed at the 16-yard line, we can determine the x-values for the vertex of the parabola.
The x-coordinate of the vertex is the average of the two x-values (10 and 16) where the balloon was released and landed:
h = (10 + 16) / 2 = 13
Since the height of the balloon reached 27 yards, we have the vertex point (13, 27)
Now, let's substitute the vertex coordinates (h, k) into the general equation:
y = a(x - 13)² + k
Substituting the vertex coordinates (13, 27)
y = a(x - 13)² + 27
To determine the value of 'a', we need another point on the parabolic path. Let's assume that the highest point reached by the balloon is the vertex (13, 27).
This means that the highest point (13, 27) lies on the parabola
Substituting the vertex coordinates (13, 27) into the equation
27 = a(13 - 13)² + 27
27 = a(0) + 27
27 = 27
Hence , the equation representing the path of Al's toss is y = a(x - 13)² + 27, where 'a' can be any real number
To learn more about parabola click :
https://brainly.com/question/24042022
#SPJ1
A statewide survey is to be made. First, the state is subdivided into counties. Seven counties are selected at random and further sampling is conventrated on these seven counties. What type of sampling is this?
a. Simple Random
b. Non-Proportional
c. Cluster
d. Stratified
Answers
The type of sampling described in the scenario is c. Cluster sampling.
Cluster sampling involves dividing the population into clusters or groups and randomly selecting some of these clusters. In this case, the state is subdivided into counties, which act as the clusters. Seven counties are selected at random, and further sampling is concentrated on these seven counties.
Cluster sampling is commonly used when it is not feasible or practical to directly sample individuals from the entire population. Instead, clusters or groups are randomly selected, and then a sample is taken from each of these clusters. This approach can be more efficient and cost-effective compared to other sampling methods, especially when the clusters are internally heterogeneous.
In this scenario, the initial random selection of the seven counties represents the cluster sampling, as subsequent sampling is focused on these specific clusters.
Learn more about Cluster sampling here:
https://brainly.com/question/30639218
#SPJ11
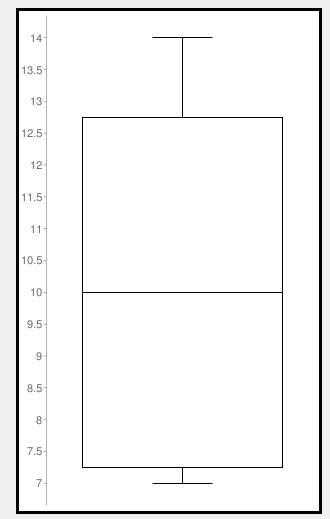
help awnser quick i need it

Answers
The statistical measures for the given set of data are:
Population size: 8
Median: 10
Minimum: 7
Maximum: 14
First quartile: 7.25
Third quartile: 12.75
Interquartile Range: 5.5
Outliers: none
The statistical measures for the given set of data are:
Mean: (7+7+8+9+11+12+13+14)/8 = 10.125
Median: 10
Mode: 7 (since it appears twice)
Range: 14-7 = 7
Variance: 6.625
Standard deviation: √(6.625) = 2.6
To create a box and whiskers plot, we first need to order the data set from smallest to largest:
7, 7, 8, 9, 11, 12, 13, 14
To find the quartiles, we need to find the median (which we already know is 10), and then find the median of the lower half and upper half of the data set separately:
Lower half: 7, 7, 8, 9
Upper half: 11, 12, 13, 14
The median of the lower half is (7+8)/2 = 7.5, and the median of the upper half is (12+13)/2 = 12.5.
Therefore, the quartiles are:
Q1 = 7.25
Q2 (median) = 10
Q3 = 12.75
To find the range of values within 1.5 times the IQR, we first calculate the IQR:
IQR = Q3 - Q1 = 12.5 - 7.5 = 5
Then, we calculate the lower and upper bounds:
Lower bound = Q1 - 1.5IQR = 7.5 - 1.55 = 0
Upper bound = Q3 + 1.5IQR = 12.5 + 1.55 = 20
Since all of the observations fall within the bounds, there are no outliers in this data set.
Using this information, we can create a box and whiskers plot as follows:
To learn more about the box-and-whisker plot ;
https://brainly.com/question/2742784
#SPJ1
Write the equation of the line, with the given properties, in slope intercept form slope = -2, through(-4,7)
Answers
Answer:
y= -2x + 7
Step-by-step explanation:
So in slope intercept y will always equal something so you start with
y= mx + b
m = slope and b = y-intercept
so in this case it would first be
y = -2x + b
and then since we have the point it passes through (-4,7) we know that the line passes through the y axis at 7 hence the y value is 7.
so you finally get
y=-2x+7
The equation of line passes through the point (-4, 7) will be;
⇒ y = - 2x - 1
What is Equation of line?The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
The point on the line are (-4, 7).
And, The slope of the line is,
⇒ m = - 2
Now,
Since, The equation of line passes through the point (- 4, 7).
And, Slope of the line is,
m = - 2
Thus, The equation of line with slope - 2 is,
⇒ y - 7 = - 2 (x - (-4))
⇒ y - 7 = - 2 (x + 4)
⇒ y - 7 = - 2x - 8
⇒ y = - 2x - 8 + 7
⇒ y = - 2x - 1
Therefore, The equation of line passes through the point (-4, 7) will be;
⇒ y = - 2x - 1
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ2
The table of values represents a quadratic function f(x).
x f(x)
−8 13
−7 6
−6 1
−5 −2
−4 −3
−3 −2
−2 1
−1 6
0 13
What is the equation of f(x)?
f(x) = (x + 5)2 − 2
f(x) = (x + 4)2 − 3
f(x) = (x − 4)2 − 3
f(x) = (x − 5)2 − 2
.
Answers
The table of values represents a quadratic function f(x), the equation of f(x) is f(x) = (x + 4)² - 3.
To determine the equation of the quadratic function f(x) based on the table of values, we can look for a pattern in the x and f(x) values.
By observing the table, we can see that the f(x) values correspond to the square of the x values with some additional constant term.
Comparing the given table with the options provided, we can see that the equation that fits the given data is:
f(x) = (x + 4)² - 3
This equation matches the f(x) values in the table for each corresponding x value.
Therefore, the equation of f(x) is f(x) = (x + 4)² - 3.
For more details regarding quadratic function, visit:
https://brainly.com/question/18958913
#SPJ1
Can someone help please

Answers
Answer:
Step-by-step explanation:

Ada' hitory teacher wrote a tet for the cla. The tet i 26 quetion long and i worth 123 point. Ada wrote two equation, where m repreent the number of multiple choice quetion on the tet, and repreent the number of eay quetion on the tet. M=26
3m8=123
Answers
There are 9 questions on the test.
Let, the number of multiple-choice questions on the test = m
the number of essay questions on the test = s
m + s = 26 .......(1)
So, We are also told that multiple choice is worth 3 points each, so the total number of points for m questions will be 3m.
As essays are worth 8 points each, so the total number of points for s questions will be 8s.
3m + 8s = 123 .......(2)
Now we will use the substitution method to solve a system of linear equations.
From equation (1) we will get,
m = 26 -s
Substituting this value in equation (2) we will get,
3 * (26- s) + 8s =123
78 - 3s + 8s = 123
5s = 123 -78
5s = 45
s = 45/5 = 9
So, there are 9 questions on the test.
Read more about the substitution method:
https://brainly.com/question/22340165
#SPJ4
The complete question is:
Ada’s history teacher wrote a test for the class.
The test is 26 questions long and is worth 123 points.
Ada wrote two equations, where m represents the
number of multiple choice questions on the test, and
s represents the number of essay questions on the test.
m+s= 26
3m + 8s = 123
How many essay questions are on the test?
help please................

Answers
Answer:
1620 cm²
Step-by-step explanation:
Area of trapezium=½(a+b)×height
Area of teapezium=½(6+18)(9)= 108 cm²
Volume of trapezoidal prism= 108×15= 1620 cm³
Answer:
1620cm^2
Step-by-step explanation:
bounded by the paraboloid z = 4 + 2x2 + 2y2 and the plane z = 10 in the first octant
Answers
As a result, the solid's volume in the first octant, which is restricted by the paraboloid z = 4 + 2 x + 2 y, is 9.
We must determine the limits of integration for x, y, and z in order to determine the volume of the solid in the first octant bounded by the paraboloid z = 4 + 2x + 2y + 2 and the plane z = 10.
At z = 10, where the paraboloid and plane overlap, we put the two equations equal and find z:
4 + 2x^2 + 2y^2 = 10
2x^2 + 2y^2 = 6
x^2 + y^2 = 3
This is the equation for a circle in the xy plane with a radius of 3, centred at the origin. We just need to take into account the area of the circle where x and y are both positive as we are only interested in the first octant.
Integrating over the circle in the xy-plane, we may determine the limits of integration for x and y:
∫∫[x^2 + y^2 ≤ 3] dx dy
Switching to polar coordinates, we have:
∫[0,π/2]∫[0,√3] r dr dθ
Integrating with respect to r first gives:
∫[0,π/2] [(1/2)(√3)^2] dθ
= (3/2)π
So the volume of the solid is:
V = ∫∫[4 + 2x^2 + 2y^2 ≤ 10] dV
= (3/2)π(10-4)
= 9π
To know more about paraboloid,
https://brainly.com/question/22665814
#SPJ11
Write in the form in a+bi

Answers
Answer:
\(4+6i-6i^2+3i^3-4i^4=6+3i\)
Step-by-step explanation:
Given the expression
\(4+6i-6i^2+3i^3-4i^4\)
as
\(i^2=-1\\\)
so
\(=4+6i-\left(-6\right)-3i-4i^4\)
Group like terms
\(=-4i^4+6i-3i+4+6\)
Add similar items
\(=-4i^4+3i+4+6\)
Add the numbers
\(=-4i^4+3i+10\)
\(=6+3i\)
Thus,
\(4+6i-6i^2+3i^3-4i^4=6+3i\)
For a normal distribution, the probability of a value being between a positive z-value and its population mean is the same as that of a value being between a negative z-value and its population mean.
Answers
For a normal distribution, the probability of a value being between a positive z-value and its population mean is indeed the same as that of a value being between a negative z-value and its population mean.
This is due to the symmetric nature of the normal distribution curve, where probabilities are mirrored around the mean.
The normal distribution is characterized by its bell-shaped curve, which is symmetric around the mean. The mean is also the midpoint of the curve, and the curve approaches but never touches the horizontal axis. The standard deviation of the distribution controls the spread of the curve.
In a normal distribution, the probability of a value being between a positive z-value and its population mean is indeed the same as that of a value being between a negative z-value and its population mean.
This is due to the symmetric nature of the normal distribution curve, where probabilities are mirrored around the mean.
This means that if we have a normal distribution with a mean of μ and a standard deviation of σ, the probability of a value falling between μ+zσ and μ is the same as the probability of a value falling between μ-zσ and μ.
This property of the normal distribution makes it easy to compute probabilities for any range of values, by transforming them into standard units using the z-score formula.
To learn more about probability, refer below:
https://brainly.com/question/30034780
#SPJ11
associative property under whole numbers and integers. with an example
Answers
Answer:
When we multiply three or more whole numbers, the value of the product remains the same when they are grouped in any manner. ... Thus, if 'a', 'b', and 'c' are three whole numbers, then a × (b × c) = (a × b) × c = (a × c) × b. For example, 6 × (7 × 2) = (6 × 7) × 2 = (6 × 2) × 7 = 84.
This property of the whole numbers tells that the order of addition does not change the value of the sum. Let a and b are two whole numbers, then a + b = b + a. Suppose a = 10 and b = 18 ⇒ 10 + 18 = 28 = 18 + 10.
Associative Property
When we add three or more whole numbers, the value of the sum remains the same. The order of addition of numbers is not important. Or, in other words, the numbers can be grouped in any manner. The sum remains the same. This is the associative property of addition.
If a, b, and c are three whole numbers, then a + (b + c) = (a + b) + c = (a + c) + b. For example, 10 + (5 + 12) = (10 + 5) + 12 = (10 + 12) + 5 = 27
Additive Identity
This is the property of zero by which the value of the whole number remains the same when added to any whole number. Zero is the additive identity of whole numbers. If w is a whole number, then w + 0 = w = 0 + w. For example, 0 + 7 = 7 = 7 + 0.
Properties of Subtraction
Closure Property
When one whole number is subtracted from another, the difference is not always a whole number. This means that the whole numbers are not closed under subtraction. If a and b are two whole numbers and a − b = c, then c is not always a whole number. Take a = 7 and b = 5, a − b = 7 − 5 = 2 and b − a = 5 − 7 = −2 (not a whole number).
Commutative Property
Subtraction of two whole numbers is not commutative. This means we cannot subtract two whole numbers in any order and get the same result. Let a and b be two whole numbers, then a − b ≠ b − a. Take a = 7 and b = 5, 7 − 5 = 2 ≠ 5 − 7 = −2.
Associative Property
An associative property does not hold for the subtraction of whole numbers. This means that we cannot group any two whole numbers and subtract them first. Order of subtraction is an important factor. If ‘a’, ‘b’, and ‘c’ are the three whole numbers then, a − (b − c) ≠ (a − b) − c. Consider the case when a = 8, b = 5 and c = 2, 8 − (5 − 2) = 5 ≠ (8 − 5) − 2 = 1.
Subtractive Property of Zero
When we subtract zero from a whole number, the value of the whole number remains the same. Take an example, a = 98, a − 0 = 98 − 0 = 98.
\(Properties of Multiplication
Closure Property
Multiplication of two whole numbers will result in a whole number. Suppose, a and b are the two whole numbers and a × b = c, then c is also a whole number. Let a = 10, b = 5, 10 × 5 = 50 (whole number). The whole number is closed under multiplication\)
.
What is (7.8×10^3) times (1.0x10^4)
PlZzzzzz help me I’m putting 20 points and give me the exact answer!
PLZZZZZZZ
Answers
Answer:
78000000
Step-by-step explanation:
Find the measures of two angles, one positive and one negative, that are coterminal with pi/6
Answers
The coterminal angle of π/6 are 390°, 750°, -330°, -690°.
What is an angle?An angle is a geometry in plane geometry that is created by 2 rays or lines that have an identical terminus.
The identical endpoint of the two rays—known as the vertex—is referenced as an angle's sides.
The angle is the measurement of the angular distance for example for linear motion we have a meter inch but for angular rotation, we don't have the measurement so the angle is useful to measure the angular rotation.
In order to find the coterminal angle of an angle, we need to add or subtract the multiple of 360°
So,
coterminal of π/6 = 30°
30 + 360 = 390°
30 - 360 = -330°
30 + 720 = 750°
30 - 720 = -690°
Hence "The coterminal angle of π/6 are 390°, 750°, -330°, -690°".
For more about the angle,
brainly.com/question/13954458
#SPJ1
A mountain grows by 2 centimeters every year. At this rate in how many years will the mountain grow by 1.3 meters?
Answers
well, let's keep in mind that a meter has 100 centimeters, thus 1.3 meters will be 1.3 * 100 cm, namely 130 cm.
\(\begin{array}{ccll} cm&year\\ \cline{1-2} 2 & 1\\ 130& x \end{array} \implies \cfrac{2}{130}~~=~~\cfrac{1}{x}\implies \cfrac{1}{65}=\cfrac{1}{x}\implies x=65\)
Studied: 87 100 94 79 92 100 95 83 89 99 100 91 89 95 100 93 96 83
Did not study: 82 72 45 91 58 83 65 87 90 77 73 89.
What is the mean of the group that did not study
Answers
Answer: 76
Step-by-step explanation: you add all the numbers than divide by the amount of numbers there is there
Answer:
76
Step-by-step explanation:
because the mean is also known as the average so according to my calculations the average of the ones that didn't study=76
on your desk, there is a very special die with a prime number p of faces, and you throw this die once. show that no two events a and b can be independent unless either a or b is the whole sample space or the empty set.
Answers
We have proven that no two events a and b can be independent unless either a or b is the whole sample space or the empty set below.
A sample space can be defined as the set of all possible outcomes of any experiment.
We are already aware that the outcomes of this die are going to be (1,2,3,..p). If we have a pair of proper events A, B which are independent, this would mean that = A∩B={∅} (i)
This is a contradiction. So, now we suppose that = A∩B=C, for some proper event C (ii)
Using the values of (i) and (ii), we get -
= |C|p=P(A∩B)=P(A)P(B)=|A||B|p2.
= p|C|=|A||B|.
From this, we understand that neither A nor B are going to be full spaces and hence, no two events a and b are independent and 0<|A|<p and 0<|B|<p. Since |C| is also going to be less than 0 and p is prime, p divides either |A| or |B|. if p was not prime (say, p=4), then you would only need the factors of p to divide either |A|,|B|, so, it becomes necessary for p to be a prime number. Hence, proved.
Learn more about sample space on
https://brainly.com/question/28043513?referrer=searchResults
#SPJ4
Please help me!! Find the value of each variable.

Answers
Answer:
Step-by-step explanation:
c = 180 - 60
= 120
a + b = 60
what expression is equivalent to 2x + 4
Answers
Answer:
4x + 8 is equivalent to the expression.
what is the area of the kite ? PLEASE HELP BEING TIMED

Answers
Answer:
7 * 4 / 2 = 28/2 = 14
Step-by-step explanation:
You are timed. I will just give you the formula where its multiplying the Diagonals and dividing by 2.
x= -4 w= 1 z= -3 y= 5
This is the answer!
HELPPPPPPPPPPPPPPPPPPP

Answers
what is the area of this triangle

Answers
Answer:
18
Step-by-step explanation:
you need to multiply the base by the height then divide it by 2
Solve for m.
m/2 = m+5/4
Answers
Answer:
m = -5/2 or -2.5
Pls choose me as brainliest!
Eleanor is working her way through school. She works two part-time jobs for a total of25 hours a week. Job A pays$6.00 per hour, and Job B pays$6.80 per hour. How many hours did she work at each job the week that she made$159.60
Answers
ANSWER
She worked 13 hours in Job A and 12 hours in Job B.
EXPLANATION
Eleanor works two part-time jobs.
Both jobs take a total of 25 hours a week.
Let the number of hours worked in Job A be x.
Let the number of hours worked in Job B be y.
This means that:
x + y = 25 _____(1)
Job A pays $6.00 per hour and Job B pays $6.80 per hour.
The total she made that week was $159.60.
This means that:
6 ^ x + 6.8 * y = 159.60
=> 6x + 6.8y = 159.6 _____ (2)
We have two simultaneous equations:
x + y = 25 _____ (1)
6x + 6.8y = 159.6 ___(2)
From (1), we have that:
x = 25 - y
Put that in (2):
6(25 - y) + 6.8y = 159.6
150 - 6y + 6.8y = 159.6
150 + 0.8y = 159.6
Collect like terms:
0.8y = 159.6 - 150 = 9.6
y = 9.6 / 0.8
y = 12 hours
Recall that:
x = 25 - y
=> x = 25 - 12
x = 13 hours
Therefore, she worked 13 hours in Job A and 12 hours in Job B.
If a sample has a small standard deviation, we can say the scores in the sample are.
Answers
If a sample has a small standard deviation, we can say the scores in the sample are consistent.
Standard deviation is a measure of dispersion. It measures the variation of the scores from the central value of the distribution.
A data is said to be consistent when this variation is less. Such data are easy to handle for studies.
When it is difficult to study the very large population, we choose samples from the population randomly. Each of these samples also have its own standard deviation. When this standard deviation is small, then the data is more consistent. That is, the scores in the sample goes well with those in the population.
Learn more about standard deviation at https://brainly.com/question/475676
#SPJ4
I need both an answer an explaination

Answers
Cos (C) is 24/25 because 24 is adjacent and 25 is the hypotenuse
Tan (C) is 7/24 because 7 is opposite and 24 is adjacent
