express: 4d divided by c + 3 ; when c=3 and d=6
Answers
the equation is:
\(\frac{4d}{c+3}\)and we replace c=3 and d=6 so:
\(\frac{4\cdot6}{3+3}=\frac{24}{6}=4\)Related Questions
If points x,y are chosen randomly from the intervals [0,2] and [0,1], respectively , then the probability That y≤x2 is
Answers
When points x,y are chosen randomly from the intervals [0,2] and [0,1], respectively, the probability that y is less than or equal to x squared, i.e., y ≤ x², is 1/3.
To solve this problem, we need to determine the area of the region where y is less than or equal to x squared. We can visualize this region by graphing the equation y = x², which is a parabola that opens upward and passes through the points (0, 0) and (1, 1).
Next, we need to find the area of the rectangle formed by the intervals [0, 2] and [0, 1], which has an area of 2.
To find the probability that y ≤ x², we need to divide the area of the region where y is less than or equal to x squared by the area of the rectangle.
To do this, we can integrate the equation y = x² with respect to x from 0 to 1, which gives us the area under the curve between x = 0 and x = 1. This integral is equal to 1/3.
Therefore, the probability that y ≤ x² is 1/3.
To know more about probability here
https://brainly.com/question/30034780
#SPJ4
2. The population of a town was 7,250 in 2014
and 7,375 in 2015. What was the percent
increase from 2014 to 2015 to the nearest
tenth of a percent?
A) 1.5%
B) 1.6%
C) 1.7%
D) 1.8%
E) 2.0%
E
Answers
The percentage change of the population is P = 1.7 %
Given data ,
To calculate the percent increase from 2014 to 2015, we need to find the difference between the two population values, divide it by the initial value, and then multiply by 100 to get the percentage.
Population increase = 7,375 - 7,250 = 125
Percent increase = (Population increase / Initial population) * 100
Percent increase = (125 / 7,250) * 100 ≈ 1.7241
Rounding to the nearest tenth of a percent, the percent increase is approximately 1.7%.
Hence , the percentage change is P = 1.7 %
To learn more about percentage click :
https://brainly.com/question/12861068
#SPJ1
five eighths of x is 2 1/2. what is x?
Answers
4
Step-by-step explanation:
8/5(put 8 as numerator becuz we need to find all x from 5/8) x 2 1/2=4
Write a function rule for the relationship between the amount of plant food remaining, f(x), and the number of days that have passed, x. Type the correct answer in the box.
Answers
Answer:
f(x) = 72-12x
Step-by-step explanation:
this might be too late but it could be useful for future people
Answer:
f(x) = 72-12x
took a while to solve.......
Angel has a deck that measures 20 feet by 25 feet. He wants to increase each dimension by equal lengths so that its area is increased by 50%. By how much should he increase each dimension?
Answers
The dimensions of the deck should be increased by 5 feet each
How to determine by how much the lengths should be increasedFrom the question, we have the following parameters that can be used in our computation:
Length = 20 feet
Width = 25 feet
So, the area is
Area = 20 * 25
Evaluate
Area = 500
When increased by 50%, we have
(20 + x) *(25 + x) = 500 * 1.50
Evaluate
(20 + x) * (25 + x) = 750
Express 750 as 25 * 30
So, we have
(20 + x) * (25 + x) = 25 * 30
This means that
20 + x = 25
25 + x = 30
Solve for x
x = 5 and x = 5
This means that
Increment = 5
Hence, the lengths should be increased by 5 feet
Read more about area at
https://brainly.com/question/24487155
#SPJ1
PHOTO ATTACHED CAN SOMEONE PLZ FR HELP LIKE NOT LIKE A LINK OR A ANSWER FOR THE POINTS I NEED SOME HELP!!!!!!!! thank you :)

Answers
Answer:
80a²b³c
Step-by-step explanation:
As with numbers, the LCM is the product of the highest-powered factors.
16ab³ = 2⁴×a×b³
5a²b² = 5×a²×b²
20ac = 2²×5×a×c
The highest power of the factor 2 is 2⁴.
The highest power of the factor 5 is 5.
The highest power of the factor a is a².
The highest power of the factor b is b³.
The highest power of the factor c is c.
The LCM is 2⁴×5×a²×b³×c = 80a²b³c
Jose’s school has 426 students. His principal has promised the Student Council that their idea will be carried out if they can get at least 25% of the student population to sign a petition. So far, 82 students have signed the petition. Jose used the following steps to write an inequality that can be used to determine the number of student signatures still needed: Step 1. Declare the variable: Let x = the number of student signatures still needed. Step 2. Create a ratio equivalent to StartFraction total number of signatures needed over total number of students in the school EndFraction : StartFraction x + 82 over 426 EndFraction. Step 3. Convert 25% to a decimal: 25% = 0.25. Step 4. Write the inequality: StartFraction x + 82 over 426 EndFraction less-than-or-equal-to 0.25. What is Jose’s error? In Step 1, x should be equal to the total number of students in the school. In Step 2, the ratio should be StartFraction x over 426 EndFraction. In Step 3, the decimal should be 0.025. In Step 4, the inequality should be StartFraction x + 82 over 426 EndFraction greater-than-or-equal-to 0.25.
Answers
Answer:
Step 4
Step-by-step explanation:
Jose's Steps are:
Step 1: Declare the variable:
Let x = the number of student signatures still needed.
Step 2: Create a ratio equivalent to:
\(\dfrac{\text{Total number of signatures needed}}{\text{Total number of students in the school}} =\dfrac{x + 82}{426}.\)
Step 3: Convert 25% to a decimal:
25% = 0.25.
Step 4: Write the inequality:
\(\dfrac{x + 82}{426}\leq 0.25\)
Since they need at least 25% of the student population to sign a petition, In Step 4, the inequality should be:
\(\dfrac{x + 82}{426}\geq 0.25\)
Answer:
(D).Step 4
Step-by-step explanation:
I got it right on edge
Where are the minimum and maximum values for f(x) = sin x + 1 on the interval [0, 2π]?A. min:z =OB. min:x=OC. min:z =max:x= = 0, 2πOD. min:z = 0, π, 2π max: z =Reset Selectionmax: 1 =2 2max:z = 0, π, 2π
![Where are the minimum and maximum values for f(x) = sin x + 1 on the interval [0, 2]?A. min:z =OB. min:x=OC.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/8AY2glp1vXAqLpWBiJHh5bKFtTI3QRyi.jpeg)
Answers
Given the function:
\(f(x)=sinx+1\)Let's find the minimum and maximum values over the interval [0, 2π].
Let's first find the derivative of the function:
\(f^{\prime}(x)=cosx\)Now set the derivative to 0 and solve for x:
\(\begin{gathered} cosx=0 \\ \\ \text{ Take the inverse cosine of both sides:} \\ x=cos^{-1}(0) \\ \\ x=\frac{\pi}{2} \end{gathered}\)The cosine function is positive in quadrants I and IV, to find the reference angle(minimum), subtract the first solution from 2π:
\(\begin{gathered} x=2\pi-\frac{\pi}{2} \\ \\ x=\frac{2(2\pi)-\pi}{2} \\ \\ x=\frac{4\pi-\pi}{2} \\ \\ x=\frac{3\pi}{2} \end{gathered}\)Plug in the values in the function to determine the minimum and maximum:
\(\begin{gathered} f(\frac{\pi}{2})=sin(\frac{\pi}{2})+1=1+1=2 \\ \\ \\ f(\frac{3\pi}{2})=sin(\frac{3\pi}{2})+1=-1+1=0 \end{gathered}\)Therefore, we have the following:
Minimum occurs at: x = 3π/2
Maximum occurs at: x = π/2
ANSWER:
\(\)Which expression is equivalent to
45x+115?
A. 15(4x+1)
B. 25(2x+3)
C. 45(x+2)
D. 54(x+1)
Answers
Answer:
5(9x+23)
Step-by-step explanation:
45x+115
5(9x+23)
Write an equation of the line that passes through (0, -1) and is perpendicular to the line y = 1/9x + 2
An equation of the perpendicular line is y =
Answers
The equation of the perpendicular line passing through (0, -1) is y = -9x - 1.
To find the equation of a line that is perpendicular to the given line y = (1/9)x + 2 and passes through the point (0, -1), we can use the fact that perpendicular lines have slopes that are negative reciprocals of each other.
The given line has a slope of 1/9. To find the slope of the perpendicular line, we take the negative reciprocal of 1/9, which is -9.
Using the slope-intercept form of a linear equation, y = mx + b, where m represents the slope and b represents the y-intercept, we can substitute the slope and the coordinates of the given point (0, -1) into the equation.
y = -9x + b
Since the line passes through the point (0, -1), we can substitute the x-coordinate as 0 and the y-coordinate as -1 into the equation:
-1 = -9(0) + b
-1 = b
Therefore, the y-intercept (b) of the perpendicular line is -1.
Putting it all together, the equation of the line that passes through (0, -1) and is perpendicular to y = (1/9)x + 2 is:
y = -9x - 1
for such more question on perpendicular
https://brainly.com/question/18991632
#SPJ11
TIME REMAINING
44:54
The table below shows the number of cars sold each month for 5 months at two dealerships.
Cars Sold
Month
Admiral Autos
Countywide Cars
Jan
4
9
Feb
19
17
Mar
15
14
Apr
10
10
May
17
15
Which statements are supported by the data in the table? Check all that apply.
The mean number of cars sold in a month is the same at both dealerships.
The median number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The range of the number of cars sold is the same for both dealerships.
The data for Admiral Autos shows greater variability.
Answers
The statements supported by the data in the table are:
The mean number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The data for Admiral Autos shows greater variability.
To determine which statements are supported by the data in the table, let's analyze the given information:
The mean number of cars sold in a month is the same at both dealerships.
To calculate the mean, we need to find the average number of cars sold each month at each dealership.
For Admiral Autos:
(4 + 19 + 15 + 10 + 17) / 5 = 65 / 5 = 13
For Countywide Cars:
(9 + 17 + 14 + 10 + 15) / 5 = 65 / 5 = 13
Since both dealerships have an average of 13 cars sold per month, the statement is supported.
The median number of cars sold in a month is the same at both dealerships.
To find the median, we arrange the numbers in ascending order and select the middle value.
For Admiral Autos: 4, 10, 15, 17, 19
Median = 15
For Countywide Cars: 9, 10, 14, 15, 17
Median = 14
Since the medians are different (15 for Admiral Autos and 14 for Countywide Cars), the statement is not supported.
The total number of cars sold is the same at both dealerships.
To find the total number of cars sold, we sum up the values for each dealership.
For Admiral Autos: 4 + 19 + 15 + 10 + 17 = 65
For Countywide Cars: 9 + 17 + 14 + 10 + 15 = 65
Since both dealerships sold a total of 65 cars, the statement is supported.
The range of the number of cars sold is the same for both dealerships.
The range is determined by subtracting the lowest value from the highest value.
For Admiral Autos: 19 - 4 = 15
For Countywide Cars: 17 - 9 = 8
Since the ranges are different (15 for Admiral Autos and 8 for Countywide Cars), the statement is not supported.
The data for Admiral Autos shows greater variability.
To determine the variability, we can look at the range or consider the differences between each data point and the mean.
As we saw earlier, the range for Admiral Autos is 15, while for Countywide Cars, it is 8. Additionally, the data points for Admiral Autos are more spread out, with larger differences from the mean compared to Countywide Cars. Therefore, the statement is supported.
Based on the analysis, the statements supported by the data are:
The mean number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The data for Admiral Autos shows greater variability.
for such more question on mean
https://brainly.com/question/14532771
#SPJ8
On a number line, which fraction would be to the right of 1/2?
A) 2/12
B) 1/3
C) 10/20
D) 16/25
Answers
Answer:
C. I hope this helps! Have a great day.
Helpppppp pleaseeeeeee I’ll give brainliest

Answers
Answer:
CCC
Step-by-step explanation:
Answer:
c
Step-by-step explanation:
Attached as an image. Please help.

Answers
The general solution of the logistic equation is y = 14 / [1 - C · tⁿ], where a = - 14² / 3 and C is an integration constant. The particular solution for y(0) = 10 is y = 14 / [1 - (4 / 10) · tⁿ], where n = - 14² / 3.
How to find the solution of an ordinary differential equation with separable variablesHerein we have a kind of ordinary differential equation with separable variables, that is, that variables t and y can be separated at each side of the expression prior solving the expression:
dy / dt = 3 · y · (1 - y / 14)
dy / [3 · y · (1 - y / 14)] = dt
dy / [- (3 / 14) · y · (y - 14)] = dt
By partial fractions we find the following expression:
- (1 / 14) ∫ dy / y + (1 / 14) ∫ dy / (y - 14) = - (14 / 3) ∫ dt
- (1 / 14) · ln |y| + (1 / 14) · ln |y - 14| = - (14 / 3) · ln |t| + C, where C is the integration constant.
y = 14 / [1 - C · tⁿ], where n = - 14² / 3.
If y(0) = 10, then the particular solution is:
y = 14 / [1 - (4 / 10) · tⁿ], where n = - 14² / 3.
To learn more on differential equations: https://brainly.com/question/14620493
#SPJ1
The lateral surface area of a triangular prism is 120 in?. If the perimeter of the base is
20 inches, what is the height?
Answers
Answer:
6
Step-by-step explanation:
A function f is defined by f(x) = 1 + 6x + x2 + 6x3 + x4 + ⋯ that is, its coefficients are c2n = 1 and c2n + 1 = 6 for all n ≥ 0. Find the interval of convergence of the series. Find an explicit formula for f(x).
Answers
From the odd-degree terms, take out one copy and rewrite the series as
\(1+6x+x^2+6x^3+\cdots=(1+x+x^2+x^3+\cdots)+5x+5x^3+\cdots\)
\(1+6x+x^2+6x^3+\cdots=(1+x+x^2+x^3+\cdots)+5x(1+x^2+\cdots)\)
Then if |x| < 1, we can condense this to
\(\displaystyle\sum_{n=0}^\infty x^n+5x\sum_{n=0}^\infty x^{2n}=\frac1{1-x}+\frac{5x}{1-x^2}=\frac{1+6x}{1-x^2}\)
Since the series we invoked here converge on -1 < x < 1, so does this one.
The explicit formula of the function f(x) is \(f(x) = \frac{1 + x + 5x}{1-x^2}\)
How to determine the explicit formula?The function definition is given as:
\(f(x) = 1 + 6x + x^2 + 6x^3 + x^4 + ...\)
Expand the terms of the expression
\(f(x) = 1 + 5x + x + x^2 + 5x^3 + x^3 + x^4 + ...\)
Split
\(f(x) = (1 + x + x^2 +x^3 + .....) + 5x + 5x^3 + .. ...\)
Factor out 5x
\(f(x) = (1 + x + x^2 +x^3 + .....) + 5x(1 + x^2) + .. ...\)
Express 1 as x^0
\(f(x) = (x^0 + x + x^2 +x^3 + .....) + 5x(1 + x^2) + .. ...\)
Express x as x^1
\(f(x) = (x^0 + x^1 + x^2 +x^3 + .....) + 5x(1 + x^2) + .. ...\)
Also, we have:
\(f(x) = (x^0 + x^1 + x^2 +x^3 + .....) + 5x(x^0 + x^2) + .. ...\)
Rewrite the series using the summation symbol
\(f(x) = \sum\limits^{\infty}_{n=0}x^n+ 5x\sum\limits^{\infty}_{n=0}x^{2n}\)
The sum to infinity of a geometric progression is:
\(S_{\infty} = \frac{a}{1- r}\)
Where:
a represents the first term, and r represents the common ratio
Using the above formula, we have:
\(\sum\limits^{\infty}_{n=0}x^n = \frac{1}{1 - x}\)
\(5x\sum\limits^{\infty}_{n=0}x^{2n} = 5x * \frac{1}{1 - x^2} = \frac{5x}{1-x^2}\)
So, we have:
\(f(x) = \frac{1}{1-x}+ \frac{5x}{1-x^2}\)
Take the LCM
\(f(x) = \frac{1 + x + 5x}{1-x^2}\)
Evaluate the like terms
\(f(x) = \frac{1 + 6x}{1-x^2}\)
Hence, the explicit formula of the function f(x) is \(f(x) = \frac{1 + x + 5x}{1-x^2}\)
Read more about geometric series at:
https://brainly.com/question/12563588
Name the property illustrated If g = 3h and 3h = 16, then g = 16
3
Answers
The property illustrated ca be classified as the transitive property of equality
Transitive property of equalityEquation are expressions separated by an equal sign. For transitive property, if two system of equation are equal, and the first is equal to the second, then they 2nd is equal to the third, they are transitive.
According to the transitive property of equality, two quantities that are equal to the same thing are equal to each other. For instance If x = 10 and 10 = y, then x = y.
Given that g = 3h and 3h = 16, then g = 16, then the property illustrated ca be classified as the transitive property of equality
Learn more on transitive property here: https://brainly.com/question/4083674
#SPJ1
ALGEBRA Ben Shield's credit card uses the unpaid-balance method to compute the finance charge at a monthly periodic rate of 1.875%. During the monthly billing cycle, Ben charged $238.75, made a payment of $300.00, and had a finance charge of $7.99. Find his unpaid balance, previous balance, and new balance.
Answers
The new balance is a credit of $ 48.78.
Since Ben Shield's credit card uses the unpaid-balance method to compute the finance charge at a monthly periodic rate of 1.875%, and during the monthly billing cycle, Ben charged $ 238.75, made a payment of $ 300.00, and had a finance charge of $ 7.99, to find his new balance, the following calculations must be performed:
Finance charge + new purchases + previous balance - payments = X 238.75 x 1.01875 + 7.99 - 300 = X 243.22 + 7.99 - 300 = X 251.21 - 300 = X -48.78 = X
Therefore, the new balance is a credit of $ 48.78.
Learn more about maths in https://brainly.com/question/3554632
Two identical gardens are to be weeded, each by a two-person team. Team A includes one gardener who could weed the garden in 2 h and another who could weed the garden in 4 h. Team B includes two gardeners, either of whom could weed the garden in 3 h. Which team will finish first? Explain.
Answers
Step-by-step explanation:
Team A time is 1 garden / ( 1 garden/ 2 hr + 1 garden/4 hr) = 1 1/3 hr
Team B = 1 / ( 1/3 + 1/3) = 1 1/2 hr
Team A wins !
Solve the equation: (a + 2)^4- 20(a + 2)^2+ 64 = 0
Answers
Answer:
Answer is 7.
Step-by-step explanation:
(a + 2)^4- 20(a + 2)^2+ 64 = 0
2a^4- 20(2a)^2+ 64 = 0
16a-20(4a)+64=0
-4a -64 -4a -64
12a-84=0
+84 +84
12a=84
84/12=7
If needed to be solved to show proof text me
What value of x makes the following equation true?
15+3x=3(2−2x)
Answers
Answer:
\(\boxed {x = -1}\)
Step-by-step explanation:
Solve for the value of \(x\):
\(15 + 3x = 3(2 - 2x)\)
-Use Distributive Property:
\(15 + 3x = 3(2 - 2x)\)
\(15 + 3x = 6 - 6x\)
-Take \(6x\) and add it to \(3x\):
\(15 + 3x + 6x = 6 + 6x - 6x\)
\(15 + 9x = 6\)
-Subtract both sides by \(15\):
\(15 - 15 + 9x = 6 - 15\)
\(9x = -9\)
-Divide both sides by \(9\):
\(\frac{9x}{9} = \frac{-9}{9}\)
\(\boxed {x = -1}\)
Therefore, the value of \(x\) is \(-1\).
Which has the greatest factor 6 and 9 or 30 and 42 or 18 and 54
Answers
Answer
18 and 54
Step-by-step explanation:
please simplify this
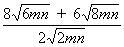
Answers
Answer:
The answer is 4√3 - 6
Steps
(8√6mn + 6√8mn ) / 2√2mn
Factor out 2√mn from the expression
That's
2√mn × ( 4√6 - 3√8) / 2√2mn
Next reduce the fraction with 2
We have
√mn × ( 4√6 - 3√8) / √2mn
Factor √2 from the denominator
√mn × ( 4√6 - 3√8) / √2(√mn)
√mn will cancel each other
we get
( 4√6 - 3√8) / √2
Simplify the radical expression
That's
( 4√6 - 3× 2√2) / √2
= ( 4√6 - 6√2) / √2
Rationalize the surd
We get
( 4√6 - 6√2) / √2 × (√2 / √2)
= ( 4√6 - 6√2) (√2) / (√2)²
= 4√12 - 12 / 2
= (8 √3 - 12) / 2
Factor out 2 from the numerator
That's
2( 4 √ 3 - 6 ) /2
2 will cancel each other
so the final answer will be
4√3 - 6
Hope this helps you
2 Write 386 in expanded form
Answers
Answer:
300+ 80+6
Step-by-step explanation:
i think i not sure
If AB is 150 then P equals?

Answers
Answer:
Wouldn't P be something less or equal to an acute angle? Try 75°.
Answer:
its 300∘ I got it right
A sub shop ordered 40 7/8 pounds of tomatoes. If they will be distributed evenly in 12 tubs. How many pounds will be in each tub
Answers
Answer:
what is it
Step-by-step explanation:
what is it?
Answer:
Step-by-step explanation:
100000$
Pleaseeeee need this quickly
50 points!

Answers
its CL i think im very sorry if im wrong
which expression is equivalent to n+n-0.18n
a. 1.18n
b. 1.82n
c. n- 0.18
d. 2n - 0.82
Answers
Answer:
Simplifying the expression `n + n - 0.18n`, we get:
n + n - 0.18n = 2n - 0.18n
Therefore, the expression `n + n - 0.18n` is equivalent to `2n - 0.18n`.
Looking at the answer choices:
a. 1.18n
b. 1.82n
c. n- 0.18
d. 2n - 0.82
We can see that choice d is equivalent to the simplified expression `2n - 0.18n`.
Therefore, the answer is d. 2n - 0.82.
Step-by-step explanation:
It’s a test so if you don’t know for sure don’t say anything

Answers
Answer:
A. |12| > √80
B. √53 > |-5.3|
Step-by-step explanation:
A. |12| > √80
The absolute value of 12 is 12, and the square root of 80 is 8.9442. This means the number sentence is true because it states that the absolute value of 12 is greater than the square root of 8.
B. √53 > |-5.3|
The square root of 53 is 7.2801 and the absolute value of -5.3 is 5.3. This means the number sentence is true because is states that the square root of 53 is greater than the absolute value of -5.3
have a nice day!
A 12 cm by 12 cm square piece of paper has 5 holes punched out of it. 4 of the holes are circles of radius 3 cm and 1 of the holes is a circle of radius 1 cm. The paper and punched holes can be visually interpreted as below. Determine the area of paper remaining after the holes have been punched out.

Answers
5 holes have been punched into a 12 cm by 12 cm square piece of paper. The area of remaining paper will be 27.714 cm².
Firstly, we will calculate the area of the square of paper in which the holes are punched.
Side of square = 12 cm
Area of square = side²
= (12) ²
= 144 cm²
Now, we will calculate the area of the bigger punch holes
Radius of big punch hole = 3 cm
Area of 1 big punch = π (radius) ²
= 22/7 × (3)²
22 / 7 × 9
= 198 / 7 cm²
Area of 4 punches = 4 × 198/7
= 792/7 cm²
Now, we will calculate the area of smaller punch whose radius is 1cm
Area = 22/7 × 1²
= 22/7 cm²
Now, we will calculate the total area covered by circles
Total area covered by circles = area of small punch + area of 4 big punch
= 22/7 + 792/7
= 814 /7 cm²
Remaining area = area of square - area of circles
= 144 - 814/7
= (1008 - 814) / 7
= 194 / 7
= 27.714 cm²
To know more about area:
https://brainly.com/question/27683633
#SPJ1