Evaluate the expression: |5-6|
Answers
Answer:
1
Step-by-step explanation:
|5 - 6|
|-1| (absolute value changes a negative number to positive)
1
Best of Luck!
Answer:
|5-6| = 1
Step-by-step explanation:
Answer inside the absolute value and you get -1. The aboslute value of -1 is 1.
Related Questions
How is 14,398 written in scientific notation?
Answers
The given number written in scientific notation is 1.4398 × 10⁴
From the question, we are to write the given number in scientific notation.
The given number is 14,398.
A number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10.
Thus,
To write the numbers in scientific notation, we will express the number as the multiplication of a number between 1 and 10 and a power of 10.
A number between 1 and 10 that can easily be formed from the number is 1.4398
Then, we can write that
14,398 = 1.4398 × 10⁴
Hence, the given number written in scientific notation is 1.4398 × 10⁴
Learn more on Scientific notation here: https://brainly.com/question/27862246
#SPJ1
What is 4x^3 multiplied by 8x^6?
Answers
Answer:
32X^9
Step-by-step explanation:
Let the vector
�
v have an initial point at
(
7
,
−
6
)
(7,−6) and a terminal point at
(
6
,
−
3
)
(6,−3). Determine the components of vector
�. V
Answers
The components of the vector with initial point (7,−6) and a terminal point at (6,−3) are:
(6, -6) to (3, -6)(7, -6) to (6, -6)How to find the components of the vectorThe components of a vector are the vectors that makes up the resultant as described in the problem to have starting point (7,−6) and terminal point (6,−3).
This can be gotten by plotting these points and getting the coordinates of the points that makes the initial point and the terminal point the hypotenuse of the triangle
From the graph, the coordinates are:
component 1: (6, -6) to (3, -6)
component 2: (7, -6) to (6, -6)
Learn more about vectors at
https://brainly.com/question/25705666
#SPJ1

Math.... Can you help

Answers
Answer: -42 7/8
Step-by-step explanation: Hope this help:D

What is the answer??

Answers
Answer:
31.4 in^2 i think
Step-by-step explanation:
Use the quadratic formula to solve for x.
2x² + 4x=1
Round your answer to the nearest hundredth.
If there is more than one solution, separate them with commas.
Answers
The solution of the equation 2x² + 4x=1 using quadratic formula is x = 0.22, -2.22
How to solve a quadratic equation using quadratic formula?A quadratic formula is a formula that provides the solution(s) to a quadratic equation.
Given a quadratic equation of the form ax²+bx+c=0, where a, b, and c are coefficients. Then, we can put the coefficients in the quadratic formula:
x = (-b±√(b²-4ac))/(2a)
Given: 2x² + 4x=1, we can rewrite it as:
2x² + 4x - 1 = 0
a = 2, b = 4 and c = -1 . Put these values in the quadratic formula:
x = (-b±√(b²-4ac))/(2a)
x = (-4±√(4²-4×2×-1))/(2×2)
x = (-4±√(16+8))/(4)
x = (-4±√24)/(4)
x = (-4±√24)/(4)
x = (-4±4.899)/4
x = (-4+4.899)/4, (-4-4.899)/4
x = 0.22, -2.22
Therefore, the solution of 2x² + 4x=1 is x = 0.22, -2.22
Learn more about quadratic formula on:
https://brainly.com/question/1214333
#SPJ1
1. Un examen de Matemáticas ha sido aprobado por 6/9 de los estudiantes. Al resto de los estudiantes le toca repetir el examen. Si el grupo está compuesto por 45 estudiantes, ¿cuántos estudiantes deben repetir dicho examen?
ayudenme mañana tengo q hacer el exameeeeeeeeen
Answers
Answer:
15 students
Step-by-step explanation:
The fraction of students who will repeat the exam is:
\(1-\frac{6}{9}\)
=\(\frac{9}{9} -\frac{6}{9} =\frac{3}{9}\)
simplified is:
\(\frac{1}{3}\)
Extract this fraction of 45:
\(45(\frac{1}{3} )=\frac{45}{3} =15\)
Hope this helps
State if these 3 numbers can be the measures of the sides of a triangle.
21, 6 , 12
Need help - Thank you!!!!
Answers
Answer:
No,because it does not go with pythagoras thorem
From a table of integrals, we know that for ,≠0a,b≠0,
∫cos()=⋅cos()+sin()2+2+.∫eatcos(bt)dt=eat⋅acos(bt)+bsin(bt)a2+b2+C.
Use this antiderivative to compute the following improper integral:
∫[infinity]01cos(3)− = limT→[infinity]∫0[infinity]e1tcos(3t)e−stdt = limT→[infinity] if ≠1s≠1
or
∫[infinity]01cos(3)− = limT→[infinity]∫0[infinity]e1tcos(3t)e−stdt = limT→[infinity] if =1.s=1. help (formulas)
For which values of s do the limits above exist? In other words, what is the domain of the Laplace transform of 1cos(3)e1tcos(3t)?
help (inequalities)
Evaluate the existing limit to compute the Laplace transform of 1cos(3)e1tcos(3t) on the domain you determined in the previous part:
()=L{e^1t cos(3)}=
Answers
"From a table of integrals, we know that for \(\(a \neq 0\)\) and \(\(b \neq 0\):\)
\(\[\int \cos(at) \, dt = \frac{1}{a} \cdot \cos(at) + \frac{1}{b} \cdot \sin(bt) + C\]\)
and
\(\[\int e^a t \cos(bt) \, dt = \frac{e^{at}}{a} \cdot \cos(bt) + \frac{b}{a^2 + b^2} \cdot \sin(bt) + C\]\)
Use this antiderivative to compute the following improper integral:
\(\[\int_{-\infty}^{0} \cos(3t) \, dt = \lim_{{T \to \infty}} \int_{0}^{T} e^t \cos(3t) \, e^{-st} \, dt = \lim_{{T \to \infty}} \text{ if } s \neq 1, \, \text{ or } \lim_{{T \to \infty}} \text{ if } s = 1.\]\)
For which values of \(\(s\)\) do the limits above exist? In other words, what is the domain of the Laplace transform of \(\(\frac{1}{\cos(3)} \cdot e^t \cos(3t)\)\)?
Evaluate the existing limit to compute the Laplace transform of on the domain you determined in the previous part:
\(\[L\{e^t \cos(3t)\\).
To know more about antiderivative visit-
brainly.com/question/9700015
#SPJ11
Answer this question please.

Answers
Answer:
what question all of them if you want to answer all of them go to a new tab and look up calculator hope i help a little
Step-by-step explanation:
Find sin J, cos J, and tan J as
a fraction in simplest form.
Find the missing side.
Round to the nearest tenth.


Answers
Answer:
sin J = \(\frac{15}{29}\)
cos J = \(\frac{21}{29}\)
tan J = \(\frac{5}{7}\)
x = 14.6
Step-by-step explanation:
1st pic:
1st, find the missing side lenght:
\(a^{2} = c^{2} - b^{2}\)
\(a^{2} = 58^{2} - 42^{2}\)
\(a^{2} = 3364 - 1764\)
\(\sqrt{a^{2}} = \sqrt{1600}\)
a = 40
sin = \(\frac{opposite}{hypothenuse}\) ⇒ \(sin J = \frac{30}{58} = \frac{15}{29}\)
cos = \(\frac{adjacent}{hypothenuse}\) ⇒ \(cosJ = \frac{42}{58} = \frac{21}{29}\)
tan = \(\frac{opposite}{adjacent}\) ⇒\(tanJ = \frac{30}{42} = \frac{5}{7}\)
2nd pic:
use sine:
sin = \(\frac{opposite}{hypothenuse}\)
sine 59 = \(\frac{x}{17}\)
sine of 59 is 0.857:
0.857 = \(\frac{x}{17}\)
multiply 17 on both sides:
0.857 x 17 = \(\frac{x}{17}\) x 17
14.569 = x
round to the nearest tenth:
14.569 = 14.6
please helpppp
also just click the image for it to be bigger

Answers
Please help I’ll give brainiest

Answers
the product of two numbers is 48. when the greater number is divided by the lesser number, the quotient is 3. write and explain how to find the two numbers
Answers
The large number is x
The small number is y
xy = 48
y/x = 3
y = 3x
4x = 48
y = 12
x = 4
a helium filled balloon has a volume of 50.0 l at 25 and 1.08 atm what volume will it have at .855 atm and 10.0 c
Answers
The volume of the helium-filled balloon at 0.855 atm and 10.0 °C will be approximately 42.81 L, calculated using the ideal gas law equation.
To compute this problem, we can use the ideal gas law, which states that PV = nRT, where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the temperature in Kelvin.
First, we need to convert the initial temperature of 25 °C to Kelvin:
T1 = 25 + 273.15 = 298.15 K
Next, we can rearrange the ideal gas law equation to solve for V2:
V2 = (P1 * V1 * T2) / (P2 * T1)
We have:
P1 = 1.08 atm (initial pressure)
V1 = 50.0 L (initial volume)
P2 = 0.855 atm (final pressure)
T2 = 10.0 °C (final temperature)
Converting the final temperature to Kelvin:
T2 = 10 + 273.15 = 283.15 K
Substituting the values into the equation:
V2 = (1.08 * 50.0 * 283.15) / (0.855 * 298.15)
V2 ≈ 42.81 L
Therefore, the volume of the helium-filled balloon at 0.855 atm and 10.0 °C will be approximately 42.81 L.
To know more about ideal gas law refer here:
https://brainly.com/question/30458409#
#SPJ11
find the velocity and acceleration vectors in terms of and . r= 2cost and theta = 9t
Answers
So the velocity vector is v = (-2sin(t)) i + (2cos(t)) j, and the acceleration vector is a = (-2cos(t)) i + (-2sin(t)) j, both in terms of t.
Given
r= 2cost and theta = 9t
To Find
the velocity and acceleration vector
Solution
We can start by expressing the position vector r in terms of the Cartesian coordinates x and y:
x = r cos(theta) = 2cos(t)
y = r sin(theta) = 2sin(t)
To find the velocity vector, we can take the time derivative of the position vector:
v = (dx/dt) i + (dy/dt) j
where i and j are the unit vectors in the x and y directions, respectively.
Taking the derivatives:
dx/dt = -2sin(t)
dy/dt = 2cos(t)
Substituting these back into the velocity vector equation:
v = (-2sin(t)) i + (2cos(t)) j
To find the acceleration vector, we can take the time derivative of the velocity vector:
a = (d^2x/dt^2) i + (d^2y/dt^2) j
Taking the derivatives:
d^2x/dt^2 = -2cos(t)
d^2y/dt^2 = -2sin(t)
Substituting these back into the acceleration vector equation:
a = (-2cos(t)) i + (-2sin(t)) j
So the velocity vector is v = (-2sin(t)) i + (2cos(t)) j, and the acceleration vector is a = (-2cos(t)) i + (-2sin(t)) j, both in terms of t.
https://brainly.com/question/31467231
Find the area of the shaded sector
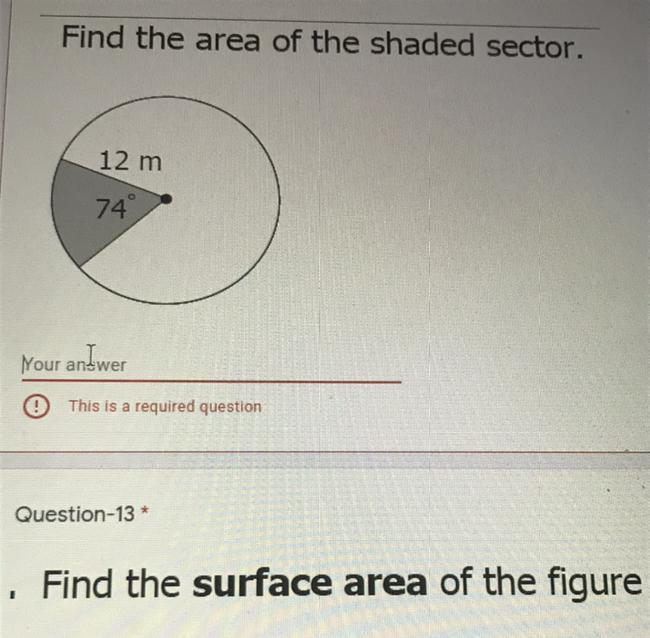
Answers
Answer:
888
Step-by-step explanation:
Im pretty sure this is the answer, if helpful please mark me as brainiest :>
A small box in the shape of a cube for packaging has a volume of 64 cubic inches.
For a medium box, the length, width, and height are all doubled. What is the ratio of the sides, area of the bases, and volumes of the boxes? Show your work.
What is the volume of a medium box? Show your work.
Ratios
Sides:
Area:
Volume:
Answers
What are the ratio of the small box to the medium box?
The first step is to determine the side lengths of the small box.
Side length = ∛64 = 4 in
Side lengths of the medium boxes = 4 x 2 = 8 inches
Volume of the medium box = 8³ = 256 cubic inches
The ratio of the sides of the small box to the medium box = 4 : 8 = 1:2.
The ratio of the area of the small box to the medium box= (4 x 4) : (8 x 8) = 1:4.
The ratio of the volume of the small box to the medium box = 4³ : 8³ = 1 : 8.
To learn more about the volume of a cuboid, please check: https://brainly.com/question/26406747
Given a and ß are the roots of the quadratic equation
-2x² - 5x + 6 = 0. Form the quadratic equation which has the roots 3x + ß and 3ß + a
Answers
The quadratic equation that has (3·x + β) ans (3·x + a) as the roots can be presented as follows;
9·x² - 7.5·x - 3 = 0
What is a quadratic equation?A quadratic equation is an equation that can be expressed in the form; y = a·x² + b·x + c, where, a ≠ 0, and a, b, and c are numbers.
The quadratic equation -2·x² - 5·x + 6 = 0, divided by a factor of -1 indicates that we get;
2·x² + 5·x - 6 = 0
The quadratic formula indicates that we get;
x = (-5 ± √(5² - 4 × 2 × (-6))/(2 × 2) = (-5 ± √(73))/4
Let a = (-5 + √(73))/4 and let β = (-5 - √(73))/4)
(3·x + ((-5 + √(73))/4)) × (3·x + (-5 - √(73))/4) = 9·x² + 3·x·(-5 - √(73))/4) + 3·x·(-5 + √(73))/4) + ((-5 + √(73))/4)) × (-5 - √(73))/4)
9·x² + 3·x·(-5 - √(73))/4) + 3·x·(-5 + √(73))/4) + ((-5 + √(73))/4)) × (-5 - √(73))/4) = 9·x² - 15·x/2 - 3 = 0
Therefore, the equation that has (3·x + β) ans (3·x + a) as roots is the equation
9·x² - 15·x/2 - 3 = 9·x² - 7.5·x - 3 = 0
Learn more on quadratic equations here; https://brainly.com/question/29179994
#SPJ1
There were 3,905 more hits on the school’s website in January than February. February had 9,854 hits. How many hits did the school’s website have during both months? a. About how many hits did the website have during January and February?
Answers
Answer:
In Jan - 13,759
In Feb - 9,854
In both - 23,613
Step-by-step explanation:
hope it helps
Help please Im giving brianless and 100 points to the person who answer and show their work thank you very much

Answers
Answer:
what's the question at the bottom
\(\\ \rm\Rrightarrow tan16.5=\dfrac{H}{13.5}\)
\(\\ \rm\Rrightarrow H=13.5tan16.5\)
\(\\ \rm\Rrightarrow H=13.5(0.296)\)
\(\\ \rm\Rrightarrow H=3.996ft\)
What is the standard equation of a circle with center (3,2) and passes through (1,2) ?
Answers
The standard equation of a circle with center (3, 2) and passes through (1, 2) is (x - 3)² + (y - 2)² = 4.
The standard equation of a circle with center (3, 2) and passes through (1, 2) can be determined as follows:
Formula: The standard equation of a circle with center (a, b) and radius r is
(x - a)² + (y - b)² = r²
Where,
The given center is (3, 2) and the given point on the circle is (1, 2).
The radius of the circle can be calculated as the distance between the center and the given point on the circle.
D = distance between (3, 2) and (1, 2)
D = √[(1 - 3)² + (2 - 2)²]
D = √4D = 2
Therefore, the radius of the circle is 2.
Substitute the values in the formula for the standard equation of a circle with center (a, b) and radius r:
(x - a)² + (y - b)² = r²(x - 3)² + (y - 2)²
= 2²(x - 3)² + (y - 2)²
= 4
To know more about the equation, visit:
https://brainly.com/question/649785
#SPJ11
Help
please answer the question

Answers
Answer:
it's D because
6/2=3
So you then divide 15/3=5
Find the general solution to y^(4) + 2y"+y = 3 + cos2t
o y = c_1cost + c_2sint + t^2 (c_3cost + c_4sint) + 3 + 1/9sin2t
o y = c_1cos2t + c_2in2t+t(c_3cos2t + c_4sin2t) + 3 +1/9 cos2t
o y = c_1cost + c_2sint + t(c_3cos2t + c_4sin2t) + 3 +9sin2t
o y = c_1cos2t + c_2sin2t + t(c_3cos2t + c_4sin2t) + 3 + 1/9cost
o y = c_1cost + c_2sint + t(c_3cost + c_4sint) + 3 + 1/9cos2t
Answers
Answer:
Step-by-step explanation:
To find the general solution to the given differential equation y^(4) + 2y" + y = 3 + cos(2t), we can follow these steps.Therefore, the correct option is:
o y = c_1cost + c_2sint + t(c_3cost + c_4sint) + 3 + (1/9)sin(2t)
1. Start by finding the complementary function by assuming y = e^(rt), where r is a constant:
Substitute this assumption into the differential equation:
r^4e^(rt) + 2r^2e^(rt) + e^(rt) = 0
Simplify the equation:
e^(rt)(r^4 + 2r^2 + 1) = 0
2. Solve the equation r^4 + 2r^2 + 1 = 0 to find the roots:
Let's substitute u = r^2:
u^2 + 2u + 1 = 0
(u + 1)^2 = 0
u + 1 = 0
u = -1
Substitute back u = r^2:
r^2 = -1
r = ±i
Therefore, the roots of the equation are r = ±i.
3. Based on the roots, the complementary function is:
y_c = c_1cos(t) + c_2sin(t) + c_3cos(t) + c_4sin(t)
= (c_1 + c_3)cos(t) + (c_2 + c_4)sin(t)
4. To find a particular solution, guess a form that matches the non-homogeneous term:
y_p = At^2 + B + Ccos(2t) + Dsin(2t)
5. Take derivatives of y_p and substitute them into the differential equation to solve for the coefficients A, B, C, and D.
6. Substituting the values of A, B, C, and D back into the particular solution y_p, we get:
y_p = t^2 + 3 + (1/9)cos(2t) + (1/9)sin(2t)
7. The general solution is the sum of the complementary function and the particular solution:
y = y_c + y_p
= (c_1 + c_3)cos(t) + (c_2 + c_4)sin(t) + t^2 + 3 + (1/9)cos(2t) + (1/9)sin(2t)
Therefore, the correct option is:
o y = c_1cost + c_2sint + t(c_3cost + c_4sint) + 3 + (1/9)sin(2t)
To know more about differential equation, visit:
https://brainly.com/question/25731911
#SPJ11
aya has 14 2/5 feet of chain. She wants to make pieces foot long math. How many can she make? b Solve the problem using decimals
Answers
Aya can make 14 mats of 1 foot long.
What is division?Division is one of the fundamental arithmetic operation, which is performed to get equal parts of any number given, or finding how many equal parts can be made. It is represented by the symbol "÷" or sometimes "/"
Given that, Aya has 14\(\frac{2}{5}\) feet of chain. She wants to make pieces foot long mat.
Let can make x mats out of the given chain, since each mat is 1 foot long, so,
1×x = 14\(\frac{2}{5}\)
x = 72/5
x = 14.4
x ≈ 14
Hence, She can make 14 mats out of the given chain.
For more references on division, click;
https://brainly.com/question/21416852
#SPJ1
From the age of a person if two fifth of his age is subtracted, the result becomes 24 years. Find the age of the person .
Answers
Answer:
40 years old.
Step-by-step explanation:
\(x - \frac{2}{5} x = 24 \\ \frac{3}{5} x = 24 \\ x = 24 \div \frac{3}{5} = 40\)
The following is an example of Partial Initialization of an array. int num]= (88, 92, 75, 95, 82): True False Moving to another question will save this response. hp
Answers
Partial initialization allows us to initialize only some elements of an array, leaving the rest with default values.
The statement you provided, `int num]= (88, 92, 75, 95, 82)`, contains syntax errors and is not a valid example of partial initialization of an array in C or C++.
To understand partial initialization of an array, let's consider a correct example. Suppose we have an integer array named `num` with a size of 10. We want to initialize the first five elements of the array with specific values, and the remaining elements should be set to 0. Here's how partial initialization would look like:
int num[10] = {88, 92, 75, 95, 82};
In this example, we declare an integer array `num` with a size of 10. We provide an initializer list inside curly braces `{}` to initialize the elements of the array. The first five elements are explicitly initialized with values `88`, `92`, `75`, `95`, and `82`. The remaining elements are automatically set to 0 because we haven't provided explicit values for them.
Partial initialization allows us to initialize only some elements of an array, leaving the rest with default values. It's particularly useful when we want to set certain values while keeping others as defaults, such as zero in the case of integers.
Learn more about integers here:
https://brainly.com/question/29766862
#SPJ11
solve by completing the square

Answers
Answer:
(6 ± √72i) / 6
Hope this helps.
Answer:
Step-by-step explanation:
3\(x^{2}\)-6x+9=0
3\(x^{2}\) +3x-9x+9=0 (splitting -6x as +3x & -9x)
3x(x+1)-9(x+1)=0
(x+1)(3x-9)=0
x=-1,3
PLEASE HELP!!
Given f(x) = x^2 - 7x + 13 and g(x) = x - 2
Solve f(x) = g(x) using the substitution method. Show your work

Answers
The value of the function f(x) = g(x) is \(x^2 -8x + 15 = 0\)
Data;
f(x) = x^2 - 7x + 13g(x) = x - 2FunctionsSolving the function above by substitution method, we just need to substitute the values where required and solve.
\(f(x) = g(x)\)
Substituting the value,
\(x^2 - 7x + 13 = x - 2\\x^2 -7x - x + 13 + 2 = 0\\x^2 -8x + 15 = 0\)
The value of the function f(x) = g(x) is \(x^2 -8x + 15 = 0\)
Learn more on functions here;
https://brainly.com/question/15602982
i will give 100 points For this activity, you will need two different coins. First, you will determine the theoretical probability of events. Then, you will flip the coins 100 times and determine the experimental probability of the events.
Flip two different coins 100 times, and record the results of each coin toss in a table like the one below:
Result Frequency
Two heads
Two tails
One head, one tail
Answer the following questions based on the data you gathered. You must show your work to receive credit.
What is the theoretical probability that a coin toss results in two heads showing?
What is the experimental probability that a coin toss results in two heads showing?
What is the theoretical probability that a coin toss results in two tails showing?
What is the experimental probability that a coin toss results in two tails showing?
What is the theoretical probability that a coin toss results in one head and one tail showing?
What is the experimental probability that a coin toss results in one head and one tail showing?
Compare the theoretical probabilities to your experimental probabilities. Why might there be a difference?
Answers
The probabilities of HH, TT, and HT or TH are 0.25, 0.25, and 0.50.
What is probability?Probability means the occurrence of a random event. The value of probability can only be from 0 to 1.
The sample space will be
Sample = 4 {HH, HT, TH, TT}
The probability of getting Head on both coins will be
P(HH) = 0.25
The probability of getting Tail on both coins will be
P(TT) = 0.25
The probability of getting one Head and one Tail will be
P(HT, TH) = 0.5
Learn more about the probability on:
brainly.com/question/795909
#SPJ1