Convert 0.128 to a percent.
Answers
Answer:
12.8% is the answer
Step-by-step explanation:
0.128 x 100
Hey there!
\(\bold{\dfrac{0.128}{1}\times \dfrac{100}{100}}\\\\\bold{Cross\ multiply\downarrow}\\\bold{0.128(100)=12.8}\\\bold{1(100)=100}\\\\\bold{\dfrac{12.8}{100}}}}\\\\\bold{Or\ you\ can\ say\downarrow}\\\\\bold{0.128\times100= \%}\\\\\bold{0.128\times100=12.8\%}}\\\\\\\boxed{\boxed{\bold{Answer: 12.8\%}}}\huge\checkmark\)
Good luck on your assignment and enjoy your day!
~\(\frak{Amphitrite1040:)}\)
Related Questions
15. A plane took off and rose at an angle of 8º with the horizontal ground. As the plane flies over a water tower, it has covered a distance from the take off point of 2000 feet. How far apart are the take off point and the water tower?

Answers
I wrote it all down so you can understand it better

The required distance between the take-off point and the water tower is 1980.1 feet.
Given that,
A plane took off and rose at an angle of 8º with the horizontal ground. As the plane flies over a water tower, it has covered a distance from the take-off point of 2000 feet.
To determine how far apart are the take-off point and the water tower.
These are the equation that contains trigonometric operators such as sin, cos.. etc.. In algebraic operation.
Here,
Now,
The distance flying over inclination is 2000 feet at an angle of 8° with horizontal.
Now,
Required horizontal distance = 2000 * cos 8°
= 1980.1 feet.
Thus, the required distance between the take-off point and the water tower is 1980.1 feet.
Learn more about trigonometry equations here:
brainly.com/question/22624805
#SPJ2
Steve read in the school newspaper that 34. 6% of students plan to attend college after graduation. Steve thinks that more than 34. 6% of students at his large school plan to go to college. To investigate, he selects a random sample of =250 students from his school to test the hypotheses
H0:pH:p=0. 346≠0. 346
where p is the proportion of students that plan to attend college after graduation.
In Steve's sample, 93 students said that they plan to go to college.
What is the value of the standardized z test statistic and P-value of the test of the given hypotheses?
Give your answer for the test statistic precise to two decimal places and give the P-value precise to four decimal places.
What decision should Steve make at the α = 0. 01 level?
Answers
Since it's a two-tailed test, P-value = 2 * 0.1271 ≈ 0.2542.
With α = 0.01, the P-value (0.2542) is greater than α, so Steve should fail to reject the null hypothesis.
How to solveSteve's hypotheses should be:
H₀: p = 0.346
H₁: p ≠ 0.346
Using the sample, we find the sample proportion (p_hat) is 93/250 = 0.372.
To calculate the z-test statistic:
z = (p_hat - p) / sqrt((p * (1 - p)) / n)
z = (0.372 - 0.346) / sqrt((0.346 * 0.654) / 250)
z ≈ 1.14
To find the P-value, use a two-tailed test and a z-table to determine the area right of z. ≈ 0.1271. Since it's a two-tailed test, P-value = 2 * 0.1271 ≈ 0.2542.
With α = 0.01, the P-value (0.2542) is greater than α, so Steve should fail to reject the null hypothesis.
The evidence is not strong enough to suggest that the proportion of students planning to attend college differs from 34.6%.
Read more about p-value here:
https://brainly.com/question/13786078
#SPJ1
unit 5 analytical applications of differentiation
Answers
Students will apply their understanding of differentiation and analytical techniques to solve real-world problems.
Unit 5 in analytical applications of differentiation typically covers topics such as finding maximum and minimum values, optimization problems, related rates, and curve sketching using differentiation techniques. These topics require an understanding of differentiation, which is the process of finding the rate at which a function changes at a specific point or interval. Analytical techniques involve using algebraic methods to solve problems, which is necessary for solving complex optimization and related rates problems.
To learn more about differentiation click here
brainly.com/question/24898810
#SPJ11
Help pleaseeee. I really need help.

Answers
Answer:
10
Step-by-step explanation:
Perform the said operations
Answer:
10
Step-by-step explanation:
16*2 = 32
32/8 = 4
4*15 = 60
60/6 = 10
10
find the dimensions of the closed rectangular box with square base and volume 8000 cubic centimeters that can be constructed with the least amount of material.
Answers
The dimensions of the closed rectangular box with a square base and volume of 8000 cubic centimeters that can be constructed with the least amount of material are 20 cm.
Let the length and width of the rectangular box with a square base be x.
and the height is y.
The volume, V = 8000 = \(x^{2} y\) --------(1)
The surface area, S = 2\(x^{2}\) + 4xy . -------(2)
S = 2\(x^{2}\) + 4xy and 8000/ \(x^{2}\) =y -------( from 1 and 2)
so, S= 2\(x^{2}\) + 4x(8000/ \(x^{2}\))
S= 2\(x^{2}\) + 32000/x
to find the least amount of material to be used, we will differentiate the surface area w.r.t x.
ds/dx= 0 = 4x - 32000/\(x^{2}\)
therefore, we have, 4x = 32000/\(x^{2}\)
4\(x^{3}\) =32000
\(x^{3}\) =8000
x=20
Hence, The dimensions of the closed rectangular box with a square base and volume of 8000 cubic centimeters that can be constructed with the least amount of material are 20 cm.
Read more about Differentiation:
brainly.com/question/29545777
#SPJ4
x+5y-10=2x solve for y
Answers
Answer:
x + 5y -10 = 2x
or, 5y = 2x - x + 10
or, 5y = x + 10
or, y = (x + 10)/5
in a class of 39 student , 25 offer Fante and 19 offer Twi. five student do not offer any of the two languages.
(I) illustrate the above information on the Venn diagram
(ii) how many students offer only Twi
Answers
The Venn diagram is given below. Then the number of students who offer only Twi will be 9.
What are Sets?Sets are groups of clearly specified components. The number of items in a finite set is denoted by a curly bracket.
In a class of 39 students, 25 offer Fante and 19 offer Twi.
Five students do not offer any of the two languages.
The Venn diagram is given below.
The number of students who offer both Fante and Twi will be
⇒ 25 + 19 - (39 - 5)
⇒ 44 - 34
⇒ 10
Then the number of students who offer only Twi will be
⇒ 19 - 10
⇒ 9
More about the sets link is given below.
https://brainly.com/question/8053622
#SPJ1

Given: AB tangent at D, AD = OD = 4 Find: Area of the shaded region

Answers
Answer:
1.72
Step-by-step explanation:
AB tangent at D, AD = OD = 4
so triangle OAD is right angle with side of 4 and 4.
area of OAD = 1/2 * 4 * 4 = 8
Angle AOD = DAO = 45 deg.
so circular sector OCD area = area of circle O * 45/360
= pi * 4 * 4 * 45/360
= 2pi
Shade area ACD = trigangle OAD - circular sector OCD
= 8 - 2pi
= 1.72
Amy said 4/9 of her teammates got hits during a recent softball game. Which decimal represents this same amount?
A 0.49
B. O 0.444
c. O 0.49
D. 0.444
Answers
Answer:
.....Your answer is D
...
.
The London Eye is a large Ferris wheel that has diameter 135 meters and revolves continuously. Passengers enter the cabins at the bottom of the wheel and complete one revolution in about 27 minutes. One minute into the ride a passenger is rising at 0.06 meters per second. How fast is the horizontal motion of the passenger at that moment?
Answers
Answer:
0.253 m/s
Step-by-step explanation:
You want to know the horizontal component of motion of a passenger riding a Ferris wheel when they are 1/27 of the way around the circle and their rate of rise is 0.06 m/s.
Angle of elevationThe wheel makes one revolution in 27 minutes, so the angular displacement is changing at the rate of (360°)/(27 min) = 13 1/3°/min.
After 1 minute, the passenger is following a path that has an angle of elevation of 13 1/3°.
Horizontal componentThe ratio of vertical speed to horizontal speed will be the tangent of the angle of elevation:
Vv/Vh = tan(13 1/3°)
Then the horizontal speed will be ...
Vh = Vv/tan(13 1/3°) = (0.06 m/s)/0.237004
Vh ≈ 0.253 m/s
The passenger's horizontal motion is about 0.253 m/s.
The rate at which an assembly line workers efficiency E (expressed as a percent) changes with respect to time t is given by E'(t)= 50-4t, where t is the number of hours since the workers shift began. Assuming that E(1)=96 find E(t).
Answers
The efficiency E (expressed as a percent) of the assembly line worker at time t hours since the worker's shift began is given by E(t) = 50t - 2t^2 + 48.
To find E(t), we need to integrate the rate function E'(t) with respect to time t:
∫E'(t) dt = ∫(50 - 4t) dt
E(t) = 50t - 2t^2 + C
where C is a constant of integration. We can determine the value of C by using the initial condition E(1) = 96:
E(1) = 50(1) - 2(1)^2 + C = 96
Simplifying this equation, we get:
C = 48
Now we can substitute C into our equation for E(t):
E(t) = 50t - 2t^2 + 48
Therefore, the efficiency E (expressed as a percent) of the assembly line worker at time t hours since the worker's shift began is given by E(t) = 50t - 2t^2 + 48.
Learn more about assembly here
https://brainly.com/question/1285060
#SPJ11
-6x – 2x = 16
The Answer is - 2
Answers
Answer:
yes the answer is x = -2
Step-by-step explanation:
Factor: 0.25x^2 - 0.16y^4
Answers
0.25x^2 - 0.16y^4
Both terms are perfect squares so use the difference of squares formula
A^2 - b^2 = (a+b)(a-b) where a = 5x and b = 4y^2
Answer is 0.01(5x + 4y^2)(5x-4y^2)
Answer:
Solution given:
0.25x^2 - 0.16y^4
[0.5x]²-[0.4y²]²
[Note: Using formula: x²-y²=(x+y)(x-y)]
(0.5x+0.4y²)(0.5x-0.4y²) is a required answer.
Find the coordinates of the vertex of the following parabola algebraically. Write your answer as an (x,y) point.
y=-x^2-6x-16
Answers
\(\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{-1}x^2\stackrel{\stackrel{b}{\downarrow }}{-6}x\stackrel{\stackrel{c}{\downarrow }}{-16} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left(-\cfrac{ -6}{2(-1)}~~~~ ,~~~~ -16-\cfrac{ (-6)^2}{4(-1)}\right) \implies \left( - \cfrac{ -6 }{ -2 }~~,~~-16 - \cfrac{ 36 }{ -4 } \right) \\\\\\ (-3~~,~~-16+9)\implies (-3~~,~~-7)\)
Are these congrent? Based, on the picture.
A. BE≅DE
B. ∠BEC≅∠DEC
C. △AEB≅△AED
D. BE≅CE
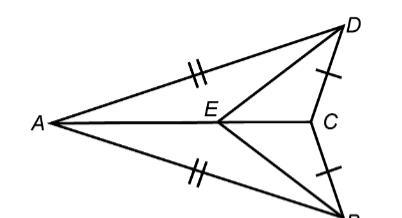
Answers
Answer:
Step-by-step explanation:
The answer is B I think
Use the distributive property to evaluate the expression
4(9 + 1)
Answers
4(9 + 1)
36 + 4
40
hope this helped
The first term in an arithmetic sequence is 5. The fourth term in the sequence is −4. The tenth term
is −22.
Which function can be used to find the nth term of the arithmetic sequence?
Answers
Answer:
aₙ = -3n + 8Step-by-step explanation:
The nth term of an arithmetic sequence: aₙ = a₁ + d(n - 1)
{d = common difference}
a₁ = 5
a₄ = 5 + d(4 - 1)
-4 = 5 + 3d
-4 - 5 = 3d
3d = -9
d = -3
Therefore;
aₙ = 5 + (-3)(n - 1)
aₙ = -3n + 8
Check: a₁₀ = 5 + (-3)(10 - 1) = 5 - 27 = - 22
The nth term of the sequence is Tn = 8 - 3n
How to determine the function of the nth term?The given parameters are:
a = 5, first term
T4 = -4 --- the 4th term
T10 = -22 --- the 10th term
The nth term of an arithmetic sequence is:
Tn = a + (n - 1) * d
So, we have:
T4 = a + (4 - 1) * d
Substitute known values
-4 = 5 +(4 -1) * d
This gives
-4 = 5 + 3d
Subtract 5 from both sides
3d = -9
Divide by 3
d = -3
Recall that:
Tn = a + (n - 1) * d
So, we have:
Tn = 5 + (n - 1) * -3
Expand
Tn = 5 + 3 - 3n
Solve
Tn = 8 - 3n
Hence, the nth term of the sequence is Tn = 8 - 3n
Read more about arithmetic sequence at:
https://brainly.com/question/6561461
Leo had $91, which is 7 times as much money as Alison had. How muchmoney did Alison have?Select the correct solution method below, where x represents Alison's money.A. 7x = 91. Divide both sides by 7. Alison had $13.B. X- 7 = 91. Add 7 to both sides. Alison had $98.C. = 91. Multiply both sides by 7. Alison had $637.D. x+ 7 = 91. Subtract 7 from both sides. Alison had $846OLDNAT
Answers
Given:
Leo had $91, which is 7 times as much money as Alison had.
Let x represents Alison's money.
So, the expression for Leo's money is,
\(7x=91\)Divide both sides of the above equation by 7.
\(\begin{gathered} \frac{7x}{7}=\frac{91}{7} \\ x=13 \end{gathered}\)So, Alison had $13.
Therefore, the correct solution method is
A) 7x = 91. Divide both sides by 7. Alison had $13.
find how long it took the sloth to travel a distance of 16 km. if it is moving at 0.24 km per hour in a westerly direction
Answers
How do you find the third side of an inequality of a triangle?
Answers
To find the third side of an inequality of a triangle, you must first use the Triangle Inequality Theorem.
This theorem states that for any triangle, the sum of any two sides of the triangle must be greater than the third side. This means that in order to find the length of the third side, you must subtract the sum of the two known sides from the smaller of the two sides, then the length of the third side will be equal to the difference between these two numbers. For example, if two sides of a triangle have lengths of 4 and 3, the third side must be greater than 1 (4 + 3 = 7 and 4 - 3 = 1). Therefore, the length of the third side must be greater than 1.
Learn more about Triangle Inequality Theorem here:
https://brainly.com/question/1163433
#SPJ4
Which density is expressed correctly to three significant figures?.
Answers
Therefore, the correct expression of the density, rounded to three significant figures, would be 2.46 g/cm³.
To express a density value to three significant figures, you need to consider the number of significant figures in the given data or measurement.
For example, if the given data or measurement has four significant figures, you would round the density value to three significant figures.
Let's consider an example:
Suppose the density of a substance is measured as 2.456 grams per cubic centimeter (g/cm³). To express this density value to three significant figures, you would round it to the nearest thousandth:
2.456 g/cm³ rounded to three significant figures is 2.46 g/cm³.
To know more about density,
https://brainly.com/question/30919299
#SPJ11
1. You draw one card from a standard 52-card deck. In how many ways could the card be a jack or a queen?
Answers
Answer:
4/52
Step-by-step explanation:
We multiply these three individual probabilities together to get P(QQQ) = P(Q)P(Q)P(Q) = (4/52)(4/52)(4/52)
HOPE THIS HELPS
Factor using the GCF. 7x + 35
7x + 35 Prime (cannot be factored)
O 7(x + 35)
O 7(7x + 5)
O 7(x + 5)

Answers
Answer:
7(x + 5)
Step-by-step explanation:
7x has the following factors: 1,7,x
35 has the following factors: 1, 5, 7, 35
the greatest common factor is 7
7(x + 5) = 7x + 35
One number added to three times another number is 24. Five times the first number added to
three times the other number is 36. Find the numbers.
Answers
Answer:
The first number is 3
The second number is 7
Step-by-step explanation:
Let x = the first number
Let y = the second (other) number
One number added to three times another number is 24:
x + 3y = 24
Make 3y the subject by subtracting x from both sides: 3y = 24 - x
Five times the first number added to three times the other number is 36:
5x + 3y = 36
Substitute 3y = 24 - x into 5x + 3y = 36 and solve for x:
5x + (24 - x) = 36
5x + 24 - x = 36
Combine like terms: 4x + 24 = 36
Subtract 24 from both sides: 4x = 12
Divide both sides by 4: x = 3
Substitute found value of x into x + 3y = 24 to find y:
3 + 3y = 24
Subtract 3 from both sides: 3y = 21
Divide both sides by 3: y = 7
What is the value of (-15/8 + 1.5) divided by (15 - 14 3/4) Please help :( this is worth my whole year grade

Answers
Answer:
-3/2 which is a
Step-by-step explanation: finding the exact value
The value (-15/8 + 1.5) ÷ (15 - \(14\frac{3}{4}\)) = -3/2,
Hence, Option A is correct.
The given expression is,
(-15/8 + 1.5) ÷ (15 - \(14\frac{3}{4}\))
Since we know,
Dividing two fractions is equivalent to multiplying the first fraction by its reciprocal. The first step in splitting fractions is to get the reciprocal of the second fraction (reverse the numerator and denominator). Then, multiply the numerators.
Here we have to find the value of the given expression is,
We can write it as,
⇒ (-15/8 + 1.5) ÷ (15 - 59/4)
⇒ (-15 + 12)/8 ÷ (60-59)/4
⇒ -3/8 ÷ 1/4
⇒ -3/8 x 4/1
⇒ -3/2
Hence,
(-15/8 + 1.5) ÷ (15 - \(14\frac{3}{4}\)) = -3/2
To learn more about division visit:
https://brainly.com/question/2273245
#SPJ6
In a survey of sports men, 64 played soccer, 94 played volleyball, 58 played basketball. 28 played soccer and volleyball, 26 played soccer and basketball, 22 played volleyball and basketball and 14 played all the three sports. Find out how many played one sport only.
Answers
Answer: 96 played one sport only.
Step-by-step explanation:
To find out how many played one sport only, we can use the principle of inclusion-exclusion.
Let S be the total number of sports men surveyed. Then, we have:
S = number who played soccer + number who played volleyball + number who played basketball - number who played soccer and volleyball - number who played soccer and basketball - number who played volleyball and basketball + number who played all three sports
Substituting the given values, we get:
S = 64 + 94 + 58 - 28 - 26 - 22 + 14
S = 154
Therefore, there were 154 sports men surveyed in total.
Now, let x be the number of sports men who played one sport only. Then, we have:
x = number who played soccer only + number who played volleyball only + number who played basketball only
Substituting the given values and using the principle of inclusion-exclusion, we get:
x = (64 - 28 - 26 + 14) + (94 - 28 - 22 + 14) + (58 - 26 - 22 + 14)
x = 22 + 58 + 24
x = 104
Therefore, there were 104 sports men who played one sport only.
Note that this includes those who did not play any of the three sports. To find out how many played at least one sport, we can subtract the number who did not play any sport from the total number surveyed:
number who played at least one sport = total number surveyed - number who did not play any sport
number who played at least one sport = 154 - (S - x)
number who played at least one sport = 154 - (154 - 14)
number who played at least one sport = 14
Therefore, there were 14 sports men who did not play any of the three sports.
Finally, to find out how many played one sport only, excluding those who did not play any sport, we can subtract 14 from 104:
number who played one sport only, excluding those who did not play any sport = 104 - 14
number who played one sport only, excluding those who did not play any sport = 90
Therefore, there were 90 sports men who played one sport only, excluding those who did not play any sport.
If the legs of a triangle are 2 and 3 inches can the hypotenuse be 4 inches ?
Answers
Answer:
No
Step-by-step explanation:
The only consecutive integers that satisfy the Pythagorean theorem are 3, 4, and 5.
___
4^2 ≠ 2^2 + 3^2
16 ≠ 4 + 9 . . . . . . . an attempt at applying the Pythagorean theorem to the given numbers fails.
I got a very large number instead of equaling 180.

Answers
Answer:
mAngleFDE = 92°
Step-by-step explanation:
Angle BDC and Angle FDB are supplementary angles, that is they add up to 180° So we can write an equation. Solve for x. Then find AngleBDC. AngleBDC and AngleFDE are equal because they are vertical angles.
8x+12+12x-32 = 180°
Combine like terms.
20x - 20 = 180
Add 20.
20x = 200
Divide by 20.
x = 10
AngleBDC
= 8x + 12
= 8(10) + 12
= 80 + 12
= 92°
AngleFDE
= AngleBDC
= 92°
Looks like the picture is not drawn to scale, but no worries. The math is all good.
A circular swimming pool has a radius of 20 feet. The family that owns the pool wants to put up a circular fence that is 5 feet away from the pool at all points. Which is closest to the circumference of the fence they will need?
Answers
Answer:
157.08 ft
Step-by-step explanation:
R = 20+5 = 25
Circumfrence = 2*pi*r = 2*pi*25 = 157.079 ft
Bobby is 5 less than Kylie's age. Their combined
age is 43. How old is Kylie?
Answers
Answer:
K=24
B=21
Step-by-step explanation:
x+x-5=43
2x=48
x=24
K=24
B=21
Answer:
24
Step-by-step explanation:
So the only way I think would be possible to get the answer is if you divide 43 by 2 (since Bobbie and Kylie are 2 people) then subtract 5 to get the answer?