factors of 12 simplify 3/4-1/3+1/2
Answers
Answer: 11/12
Step-by-step explanation: hope this helps!
Answer:
\(\frac{11}{12}\)or\(0.91¯6\)
Related Questions
PLEASE HELP A rectangle has sides that are 7 2/5
inches wide and 11 2/3
inches long. What is the perimeter of the rectangle?
Answers
Answer:
3 ways to right it. (1.) 572/15 (2.) 38.33333 repeating (3.) 38 2/15
Step-by-step explanation:
Perimeter means you add all the sides.
Step 1. Convert them to improper fractions
7 2/5 - 37/5
11 2/3 - 35/3
Step 2. Combine fractions with similar denominators.
37/5 + 37/5 & 35/3 + 35/3
74/5 & 70/3
Step 3. Find Common denominators.
74/4 x 3/3 & 70/3 x 5/5
222/15 & 350/15
Step 4. Add.
222/15 + 350/15
572/15
a = 12.9 cm, = 9.4 cm and c = 6.9 cm for the triangle shown below.Work out the value of x rounded to 1 DP.The diagram is not drawn to scale.

Answers
Answer: do u want my love
Step-by-step explanation:
Given f(x)=x*-x³-6x², for what values of x will f(x) > 0?
Answers
The values of x will f(x) > 0 for x < 0, and f(x) < 0 for -6 < x < 0 and x > -6.
To determine the values of x for which f(x) > 0, we need to find the intervals where the function is positive. Let's analyze the function f(x) = x*-x³-6x².
First, let's factor out an x from the expression to simplify it: f(x) = x(-x² - 6x).
Now, we can observe that if x = 0, the entire expression becomes 0, so f(x) = 0.
Next, we analyze the signs of the factors:
1. For x < 0, both x and (-x² - 6x) are negative, resulting in a positive product. Hence, f(x) > 0 in this range.
2. For -6 < x < 0, x is negative, but (-x² - 6x) is positive, resulting in a negative product. Therefore, f(x) < 0 in this range.
3. For x > -6, both x and (-x² - 6x) are positive, resulting in a negative product. Thus, f(x) < 0 in this range.
For such more questions on values
https://brainly.com/question/843074
#SPJ8
What is the center of the circle whose diameter has endpoints (18, -13) and (4, -3)?
Answers
Answer:
Step-by-step explanation:
The center of the circle whose diameter has endpoints (18, -13) and (4, -3) will be the midpoint of the coordinates.
The ormua for calculating mid point is expressed as;
M(X,Y) ={(x21+x2/2, y1+y2/2}
X= x1+x2/2
Y = y1+y2/2
From the coordinates
x1 = 18 x2 = 4
X= 18+4/2
X = 22/2
X = 11
y1= -13, y2= -3
Y = -3-13/2
Y = -16/2
Y = -8
Hence the required centre will be at (11,-8)
Match the equation with its graph. Identify the slope and the y intercept. y=2x+1
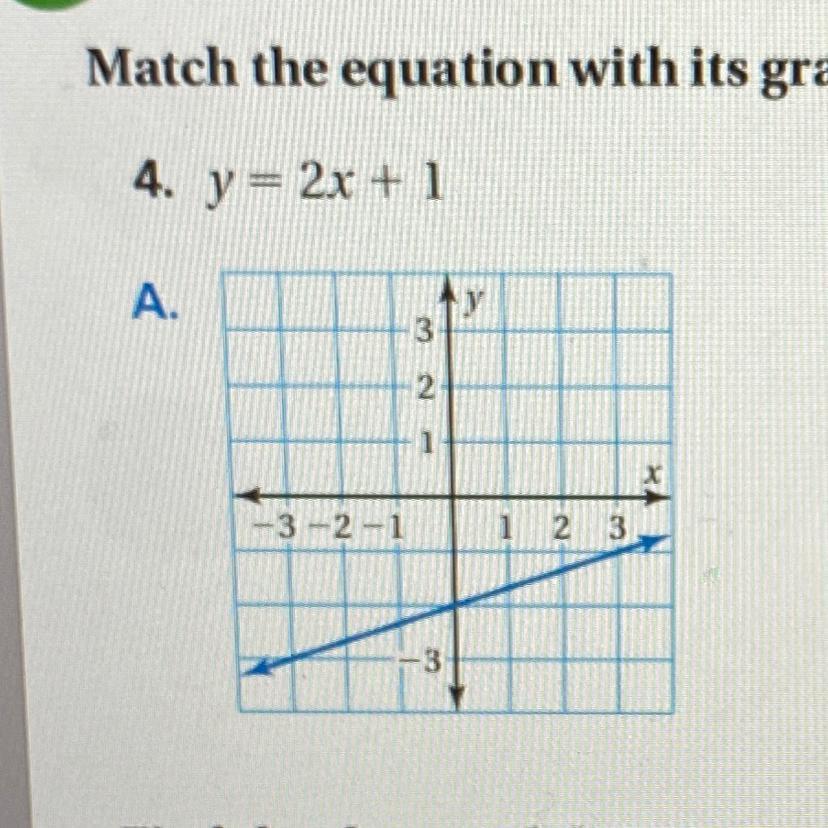
Answers
Answer:
Step-by-step explanation:
Can you show me all other answer choices? I know obviously that A) isn't the right answer.
1. Det. the discharge of a rectangular 2) flume 3m wide. 1.5m deep on ure ne 0.013. slope of as 0.0025. Find also the boundary shear stress. Solution:
Answers
Given data:Width of flume (B) = 3 mDepth of flume (D) = 1.5 mChezy’s constant (C) = 0.013Slope of the bed (S) = 0.0025We know that,Q = (1/C) * A * R^(2/3) * S^(1/2)
Where,Q = Discharge of rectangular flumeA = Area of cross-sectionR = Hydraulic radiusS = Slope of the bedCalculation:Area of cross-section, A = B * D = 3 * 1.5 = 4.5 m²Wetted perimeter, P = B + 2 * D = 3 + 2 * 1.5 = 6 mHydraulic radius,
R = A / P = 4.5 / 6 = 0.75 mSubstituting the given values,Q = (1 / 0.013) * 4.5 * 0.75^(2/3) * 0.0025^(1/2)Q = 0.796 m³/sBoundary shear stress, τo = ρ * g * R * Sρ = Density of water = 1000 kg/m³g = Acceleration due to gravity = 9.81 m/s²Substituting the given values,τo = 1000 * 9.81 * 0.75 * 0.0025τo = 18.23 N/m²
The discharge of a rectangular flume 3 m wide and 1.5 m deep on a slope of 0.0025 is 0.796 m³/s and the boundary shear stress is 18.23 N/m².
To know about Acceleration visit:
https://brainly.com/question/30660316
#SPJ11
find the value of x , please

Answers
x= 15
4x+8x: 180
12x: 180
x: 180/12
x: 15
pls give brainlist
have a great day :)
Answer:
x=15
Step-by-step explanation:
we know that 8x+4x= 180 so then we add 8x to 4x and we get 12x then we divide 180 by twelve and 12x by twelve to get that x=15
Subtract the sum of -4/7 and -5/7 from the sum of 1/2 and -21/22
Answers
The value of the fraction -5/7 and -4/7 added and subtracted from the fraction -21/2 added to 1/22 is 64/77.
The sum of 1/2 and -21/22 can be found by finding a common denominator,
1/2 = 11/22 (since 11 x 2 = 22)
-21/22 = -21/22
Therefore, the sum of 1/2 and -21/22 is,
= 11/22 - 21/22
= -10/22 = -5/11
The sum of -4/7 and -5/7 is,
-4/7 - 5/7 = -9/7
Now, subtracting as asked in the question.
= (-5/11)-(-9/7)
= (-5/11)+(9/7)
Finding common denominator to add the fractions,
7 x 11 = 77
(-5x7)/(11x7)+(9x11)/(7x11)
= -35/77 + 99/77
Now, we can combine the numerators,
-35/77 + 99/77 = 64/77
Therefore, the final answer is 64/77.
To know more about common denominator, visit,
https://brainly.com/question/19249494
#SPJ4
show that solutions to x 0 = sin(tx) are even
Answers
The solutions to the equation x(0) = sin(tx) are not even, as the sine function is an odd function, not an even function.
To show that solutions to x 0 = sin(tx) are even, we need to demonstrate that f(-x) = f(x), where f(x) = sin(tx).
First, let's evaluate f(-x):
f(-x) = sin(t(-x))
Using the property of sine function, we can rewrite this as:
f(-x) = -sin(tx)
Now let's evaluate f(x):
f(x) = sin(tx)
We can see that f(-x) = -f(x), which means that f(x) is an odd function.
However, we want to show that f(x) is an even function. To do this, we need to show that f(x) = f(-x).
Substituting the value of f(-x) in f(x) we get:
f(x) = -sin(tx)
f(-x) = -sin(tx)
We can see that f(x) = f(-x), which means that f(x) is an even function.
Therefore, we have shown that solutions to x 0 = sin(tx) are even.
Hi! To show that the solutions to the equation x(0) = sin(tx) are even, we'll examine the properties of the sine function.
Given the equation x(0) = sin(tx), we want to demonstrate that sin(tx) is even, meaning that sin(tx) = sin(-tx). This can be shown by using the properties of sine and even functions.
Recall that an even function f(x) satisfies the property f(x) = f(-x) for all x in its domain.
Now, consider the sine function sin(-tx). Using the oddness property of sine, we can rewrite this as sin(-tx) = -sin(tx). Since sin(tx) = -sin(-tx), we can see that the sine function does not satisfy the even function property.
Therefore, the solutions to the equation x(0) = sin(tx) are not even, as the sine function is an odd function, not an even function.
To learn more about function visit;
brainly.com/question/12431044
#SPJ11
Differentiate
\( \frac{ {x}^{3} + 2x ^{2} }{x} \)
with respect to their variable.
Answers
Answer:
2x + 2
Step-by-step explanation:
Given
\(\frac{x^3+2x^2}{x}\) ( divide each term on the numerator by x )
= x² + 2x
Differentiate each term using the power rule
\(\frac{d}{dx}\) (a\(x^{n}\) ) = na\(x^{n-1}\) , then
\(\frac{d}{dx}\) (x² + 2x ) = 2x + 2
please help me I dont know the answer
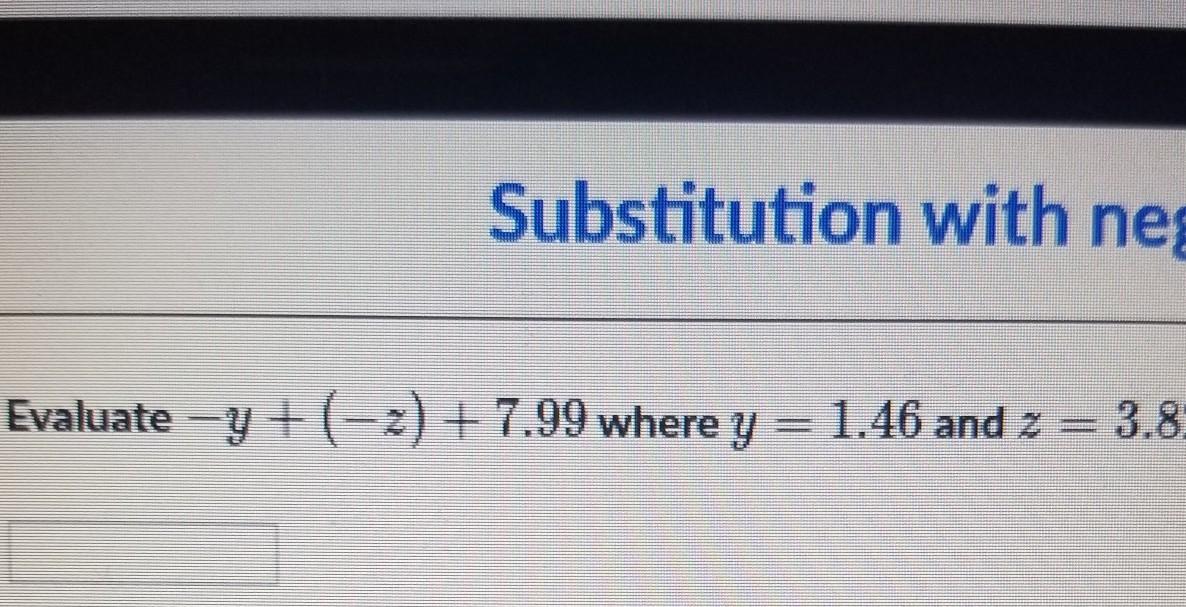
Answers
Answer:
2.71
Step-by-step explanation:
Its as simple as plugging in the values of y and z.
THis would give you
-1.46 + (-3.82) + 7.99
This plus^ you can think about having a 1 in front of it like
-1.46 + 1 (-3.82) +7.99
Multiple positive 1 with -3.82 1 times any value is that number, and positive times negative is negative. then looking like this:
-1.46 - 3.82 + 7.99 plug into a calculator and you get +2.71
Answer:
2.71
Step-by-step explanation:
We'll add the first value and the value in parentheses, being -3.82, then we'll add y, which is a negative because "-y", being -1.46. That becomes -5.28.
We'll then take our -5.28 and add 7.99, which will become 2.71.
Therefore, 2.71 is your answer.
The lateral area of a cone is 19.2π in2. The radius is 2.4 in. Find the slant height.
Answers
The slant height of a cone with lateral surface are of 19.2π inches squared and radius of 2.4 inches is 8 inches.
Lateral surface area of a coneThe formula for the lateral surface area of a cone is described as follows:
Lateral area = πrl
where
r = base radiusl = slant heightTherefore,
Lateral area = 19.2π inches²
r = 2.4 inches
Lateral area = π × 2.4 × l
19.2π = 2.4πl
divide both sides by 2.4π
l = 19.2π / 2.4π
l = 8 inches
learn more on cone here: https://brainly.com/question/27170515
If cos f° = four ninths and the measure of segment xw is 16 units, what is the measure of segment xy? triangle xyw in which angle w is a right angle, angle x measure f degrees, and angle y measures d degrees 16 units 27 units 30 units 36 units
Answers
The measure of the segment xy of the given right angle triangle is; 36 units
How to use trigonometric ratios?This question can be best understood if the trigonometric ratios are briefly highlighted since it has been used in the question. Cos f is given as 4/9. We know that the cos of an angle is derived as the adjacent divided by the hypotenuse. In other words, the cosine of angle f is given as;
Cos f = Adjacent / Hypotenuse
Thus;
Cos f = 4/9
From the triangle shown in the attachment, the adjacent is XW while the hypotenuse is XY. Hence, the adjacent is 16 units and the hypotenuse is unknown. Since the measurements given in the question are a ratio of the original dimensions, the relationship can be expressed as follows;
4/9 = 16/XY
Where XY is the unknown side
By cross multiplication, you now arrive at,
4XY = 9 * 16
XY = 144/4
XY = 36
Therefore, XY measures 36 units
Read more about trigonometric ratios at; https://brainly.com/question/13276558
#SPJ1

Solve right triangle ABC given the following: C = 90° , B = 53°, b = 23.
Round to the nearest tenth when necessary.
Answers
c=28.79912
A=37
area=199.31505
pls give brainliest if someone else comments :)
Can y’all help me please like bro omg idk

Answers
5: quadratic
6: exponential
7: inverse variation
Answer:
#4. linear
#5. quadratic
#6. exponential
#7. inverse
Determine the intervals on which f(x) is continuous.
f(x)=4sin(x²+47)
Answers
f(x) = 4sin(x²+47) is continuous everywhere, there are no intervals on which it is discontinuous. In other words, the function has no sudden jumps or breaks in its graph, and it can be graphed smoothly for all real values of x.
The function f(x) = 4sin(x²+47) is continuous for all real values of x. To understand why, we need to review the definitions of continuity and trigonometric functions.
A function f(x) is continuous at a point x = a if the limit of f(x) as x approaches a exists and is equal to f(a). A function is continuous on an interval (a,b) if it is continuous at every point between a and b.
The sine function sin(x) is a periodic function that oscillates between -1 and 1 as x varies from negative infinity to positive infinity. It is also a continuous function, meaning it does not have any sudden jumps or breaks in its graph.
The function inside the sine function in f(x) = 4sin(x²+47), namely x²+47, is also continuous for all real values of x. This is because it is a quadratic function, which is a smooth, continuous curve. Therefore, the composition of these two continuous functions, sin(x²+47) and 4sin(x²+47), is also continuous for all real values of x.
Since f(x) = 4sin(x²+47) is continuous everywhere, there are no intervals on which it is discontinuous. In other words, the function has no sudden jumps or breaks in its graph, and it can be graphed smoothly for all real values of x.
Learn more about intervals here:
https://brainly.com/question/29179332
#SPJ11
Find the perimeter.
x + 7y units
4x2 - x + 5y units
Answers
Answer:
4x^2 + 12y
Step-by-step explanation:
x + 7y + 4x^2 - x + 5y
4x^2 + 12y
12 more than quotient of a number k and 5
Answers
Answer:
(k/5)+12 represents the question described
The required equation is 12 + k/5.
What is an equation?In mathematics, an equation is a formula that expresses the equality of two expressions by connecting them with the equal sign = .
Now the given statement is,
12 more than quotient of a number k and 5
Converting them into numerical form,
quotient of a number k and 5 = k/5
Therefore 12 more than quotient of a number k and 5 is written as,
12 + k/5
this is the required equation for the given statement.
Thus, the required equation is 12 + k/5.
To learn more about equation:
https://brainly.com/question/4915174
#SPJ2
This table represents a relationship between x and y, where x is the independent variable.
x 20 40 60 80 100
y 10 20 30 40 50
Which equation represents the relationship between x and y?
Responses
y = x + 10
y, = , x, + 10
y=12x
y equals one half x
y=x−10
y equals x minus 10
y = 2x
Answers
Answer:
its 21
Step-by-step explanation:
Calculate the iterated integral. (1 4xy) dx dy Step 1 When calculating e find the inner integral first. Since this is an integral with respect to x, then we consider x to be the variable and y to be a constant. Therefore, (1 + 4xy) dx dy
Answers
The first step of calculating the iterated integral involves finding the inner integral by integrating the integrand with respect to the variable x while considering y as a constant. This yields x + 2xy²
To calculate the iterated integral ∫∫(1 + 4xy) dxdy, we follow the process of integrating the inner integral first. In this case, x is treated as the variable while y is considered a constant.To find the inner integral, we integrate (1 + 4xy) with respect to x. Treating y as a constant, we obtain the integral ∫(1 + 4xy) dx. Integrating this expression yields x + 2xy² as the result.
Now, we have an expression for the inner integral: x + 2xy². The next step is to integrate this result with respect to y while considering the limits of integration for y. Without specific limits provided, we cannot determine the exact values for the integral. However, we can express the iterated integral in terms of the variable y, resulting in ∫(x + 2xy²) dy.
To learn more about iterated integral click here : brainly.com/question/31851695
#SPJ11
find the equation of the hyperbola with vertices (2,5) and (2,−3) and foci (2,10) and (2,−8).
Answers
The equation of the hyperbola is (y - 1)^2 / 16 - (x - 2)^2 / 65 = 1
To find the equation of the hyperbola, we need to determine its center, vertices, and foci.
Given:
Vertices: (2, 5) and (2, -3)
Foci: (2, 10) and (2, -8)
The center of the hyperbola is the midpoint between the vertices, which can be found by averaging their x-coordinates and y-coordinates:
Center: (2, (5 + (-3))/2) = (2, 1)
The distance between the center and the vertices is denoted by "a". In this case, the distance is the absolute value of the difference between the y-coordinates of the center and one of the vertices:
a = |1 - 5| = 4
The distance between the center and the foci is denoted by "c". In this case, the distance is the absolute value of the difference between the y-coordinates of the center and one of the foci:
c = |1 - 10| = 9
The relationship between "a", "b", and "c" in a hyperbola is given by the equation:
c^2 = a^2 + b^2
Solving for "b^2", we have:
b^2 = c^2 - a^2
= 9^2 - 4^2
= 81 - 16
= 65
Now we have all the necessary information to write the equation of the hyperbola in standard form:
For a horizontal hyperbola:
(x - h)^2 / a^2 - (y - k)^2 / b^2 = 1
For a vertical hyperbola:
(y - k)^2 / a^2 - (x - h)^2 / b^2 = 1
Since the given foci have the same x-coordinate, the hyperbola is vertical. Plugging in the values:
(y - 1)^2 / 4^2 - (x - 2)^2 / √65 = 1
Simplifying, we have:
(y - 1)^2 / 16 - (x - 2)^2 / 65 = 1
Therefore, the equation of the hyperbola is:
(y - 1)^2 / 16 - (x - 2)^2 / 65 = 1
To learn more about hyperbola go to:
https://brainly.com/question/15697124?referrer=searchResults
#SPJ11
You and your friends are going to the annual Boatnik Fair to play games and ride the rides. You are going there with $20, which is unfortunately not enough for a wristband. If every carnival-style game costs $3, and every ride costs $2, how many rides can you go on if you want to play 4 carnival games? What about if you play just 2 carnival games?
Answers
7 rides second
OMG PLS HELP I SWEAR ITS NOT THAT HARD please yall?
Proving angles are congruent; write a two column proof

Answers
Using the Side Angle Side Theorem, ∆KWL ≅ ∆ALW.
In the given question we have to
Prove: ∆KWL ≅ ∆ALW
Given: ∠KWL ≅ ∠WLK, ∠AWL ≅ ∠WLK
As given that
∠KWL ≅ ∠WLK
∠AWL ≅ ∠WLK
WL = WL (Diagonal)
Equal Parallel Sides
WK = AL
WA = KL
From Corresponding Angle Theorem
∠KWL=∠WLK and ∠AWL = ∠WLK
So ∠W=∠L
So from the Side Angle Side(SAS) Theorem
∆KWL ≅ ∆ALW.
To learn more about Side Angle Side Theorem link is here
brainly.com/question/1411515
#SPJ1
Simplify the expression if possible 4^3 × 4^5 and write you answer as a power ( using exponents )
Answers
Answer:
4^8
Step-by-step explanation:
If you are multiplying two bases that are the same with different exponents, the exponents get added and the base stays the same:
\(x^a*x^b=x^{a+b}\\\\4^3*4^5=4^{3+5}\\\\4^3*4^5=4^8\)
Therefore, 4^3 * 4^5 = 4^8
Match each expression with its value. −9 7 −2 Undefined h( 3.999 ) h(4) h(4.0001) h(9)
Answers
The values are: -9, 7, -2, Undefined, Undefined, 8, Undefined, Undefined.
Let's match each expression with its corresponding value:
Expression: -9
Value: -9
Expression: 7
Value: 7
Expression: -2
Value: -2
Expression: Undefined
Value: Undefined
Expression: h(3.999)
Value: Undefined
Expression: h(4)
Value: 8
Expression: h(4.0001)
Value: Undefined
Expression: h(9)
Value: Undefined
Now let's explain the reasoning behind each value:
The expression -9 represents the number -9, so its value is -9.
Similarly, the expression 7 represents the number 7, so its value is 7.
The expression -2 represents the number -2, so its value is -2.
When an expression is labeled as "Undefined," it means that there is no specific value assigned or that it does not have a defined value.
For the expression h(3.999), its value is undefined because the function h(x) is not defined for the input 3.999.
The expression h(4) has a value of 8, indicating that when we input 4 into the function h(x), it returns 8.
Similarly, the expression h(4.0001) has an undefined value because the function h(x) is not defined for the input 4.0001.
Lastly, the expression h(9) also has an undefined value because the function h(x) is not defined for the input 9.
For more such questions on values
https://brainly.com/question/843074
#SPJ8
In a recent study of a bee hive, it was found that there were a total of 4,109 bees, not including the queen. There were thirty‑three more nurses than drones. The number of workers was twelve more than six times the number of drones. How many of each type of bee were in the hive?
Answers
Answer:
There were 508 drones, 541 nurses and 3060 workers.
Step-by-step explanation:
Total number of bees = 4109
Let the number of drones, nurses and workers be represented by x, N and W respectively.
But,
N = x + 33 .......... 1
W = 6x + 12 .......... 2
So that,
x + (x + 33) + (6x + 12) = 4109
x + x + 33 + 6x + 12 = 4109
8x + 45 = 4109
8x = 4064
x = \(\frac{4064}{8}\)
= 508
x = 508
From equation 1,
N = 508 + 33
= 541
N = 541
From equation 2,
W = 6x + 12
= 6(508) + 12
= 3060
W = 3060
= 3060
In the hive, there were 508 drones, 541 nurses and 3060 workers.
find the exact values of the sine, cosine, and tangent of the angle. 255° = 300° − 45°
Answers
The exact values of the sine, cosine, and tangent of the angle 255° are -1/√2, 1/√2, and -1, respectively.
To find the exact values of the sine, cosine, and tangent of the angle 255°, we can use the identity that relates the trigonometric functions of an angle to the trigonometric functions of its complement.
By expressing 255° as the sum of 300° and -45°, we can determine the exact values of the trigonometric functions for the given angle.
We know that the sine, cosine, and tangent of an angle are periodic functions, repeating every 360 degrees. To find the exact values of the trigonometric functions for 255°, we can express it as the sum of 300° and -45°, where 300° is a multiple of 360°.
Since the sine, cosine, and tangent functions are odd or even functions, we can use the values of the trigonometric functions for 45° to determine the values for -45°.
For 45°:
sin(45°) = cos(45°) = 1/√2
tan(45°) = 1
Since cosine is an even function, cos(-45°) = cos(45°) = 1/√2.
Since sine is an odd function, sin(-45°) = -sin(45°) = -1/√2.
Using the definition of tangent as the ratio of sine to cosine, tan(-45°) = sin(-45°) / cos(-45°) = (-1/√2) / (1/√2) = -1.
Therefore, for the angle 255°:
sin(255°) = -1/√2
cos(255°) = 1/√2
tan(255°) = -1
Learn more about trigonometric functions here:
brainly.com/question/28483432
#SPJ11
Find the least common multiple
(LCM) of 7, 9, and 21.
Answers
Explanation: trial and error of comparing
Two motorcycle dealers sell the same motorcycle for the same original price. Dealer A advertises that the motorcycle is on sale for 7.5% off the original price. Dealer B advertises that it is reducing the motorcycle’s price by $599. When Bonnie compares the sale prices of the motorcycles in both dealers, she concludes that the sale prices are equal.
Let p represent the motorcycle’s original price.
Which equation models this situation?
Answers
The original price of the motorcycle is approximately $7,987.
Here, we are given that p represent the motorcycle’s original price.
The sale price of Dealer A will be-
7.5% less that the original price
= 92.5% of p
= 0.925p
Similarly, the sale price of dealer B will be-
$599 less than original price
= (p - 599)
Now, these two prices are equal, so we can equate the two-
0.925p = (p - 599)
0.925p = p - 599
0.925p - p = -599
-0.075p = -599
p = -599/-0.075
p = 599/0.075
p = 599000/75
p = 7,986.67
Thus, the original price of the motorcycle comes out to be approximately $7,987.
Learn more about sale price here-
https://brainly.com/question/7459025
#SPJ1
A candy company designs a package to hold chocolates. The height of the container is 13 inches and the diameter of its bottom is 9 inches.
13 in
Which shape best models the package, and what is the approximate surface area of the package?
The best model for the package is a
The approximate surface area is
square inches.
Answers
Answer:
cone,258
Step-by-step explanation:
i got it right