9x + 3y = -15
-18x - 6y = 30
X = ?
Y = ?
Answers
Answer:
I dont know why the answers are the same thats how i got the answer solving them
Step-by-step explanation:
answer for 9x+3y=-15
is
x=-5/3 -y/3
y= -5 - 3x
answer for -18x-6y=30
is
x=-5/3 - y/3
y= -5-3x
Related Questions
Help plz:))) I’ll mark u brainliest
In less then 1m after you help me ;))))

Answers
4⁄5 x + 15 = 3⁄10 x + 21
Answers
Answer:
x = 12
Step-by-step explanation:
If you're bored of solving equations the normal way, why not try this fun and easy method? Just follow these simple steps:
Subtract 3/10 x from both sides to eliminate the x term on the right side. This is like getting rid of the annoying person who always sits next to you in class.
4/5 x - 3/10 x + 15 = 21
Simplify the left side by finding the common denominator and combining the fractions. This is like putting all your candy in one bag and eating it faster.
(8/10 - 3/10) x + 15 = 21
5/10 x + 15 = 21
Subtract 15 from both sides to isolate the x term on the left side. This is like taking away your allowance and making you do chores.
5/10 x = 21 - 15
5/10 x = 6
Multiply both sides by 10/5 to solve for x. This is like giving you a magic wand that makes everything easier.
(10/5) (5/10) x = (10/5) (6)
x = 12
This is the solution of the equation. You can check it by plugging it back into the original equation and verifying that both sides are equal. Or you can just trust me
✧☆*: .。. That's all folks, have fun with math! (✧ω✧) .。.:*☆✧
A video game arcade offers a yearly membership with reduced rates for game play. A single membership costs $60 per year. Game tokens can be purchased by members at the reduced rate of $1.00 per 10 tokens. Which statements represent the function of the yearly cost in dollars, y, based on x, the number of game tokens purchased for a member of the arcade? Select three answers. The slope of the function is $1.00. The y-intercept of the function is $60. The function can be represented by the equation y = y equals StartFraction 1 Over 10 EndFraction x plus 60.X + 60. The domain is all real numbers. The range is {y| y ≥ 60}.
Answers
Answer:
2. The y-intercept of the function is $60
3. The function can be represented by the equation y = (1/10)x +60.
5. The range is y ≥ 60
Step-by-step explanation:
The function of the yearly cost in dollars, y, based on x, the number of game tokens is:
\(y=\frac{1.00}{10}x+60\\ y=0.10x+60\)
1. The slope of the function is $1.00.
The slope of the function is the cost per token, if 10 tokens cost $1.00, than the slope of the function is $0.10. This statement is incorrect.
2. The y-intercept of the function is $60
The y-intercept is the value of y for which x = 0 (If no tokens are bought). In this case, that would be the single membership cost, which is $60. This statement is correct.
3. The function can be represented by the equation y = (1/10)x +60.
As previously mentioned, this equation is correct since it represents the membership cost plus the cost of each token multiplied by the number of tokens bought.
4. The domain is all real numbers
Real numbers include fractions and negative values, which cannot be a possible value for x. Therefore, the actual domain is all natural numbers (non-negative integers). This statement is incorrect.
5. The range is y ≥ 60
The range is all of the possible values of y. The minimum value is the cost of membership with no tokens ($60), and there is no maximum value since infinite tokens could be bought theoretically. This statement is correct.
The statements that represent the function of the yearly cost in dollars, y, based on x, the number of game tokens purchased for a member of the arcade are;
B) The y-intercept of the function is $60
B) The y-intercept of the function is $60C) The function can be represented by the equation y = (1/10)x +60.
B) The y-intercept of the function is $60C) The function can be represented by the equation y = (1/10)x +60.E) The range is y ≥ 60
The equation of a line in slope intercept form is generally written as;
y = mx + c
Where;
m is slope
c is y-intercept
x is the input variable or domain
y is the output variable or range
Now, we are told that a single membership costs $60 per year. This is the price before any input which in this case game tokens are purchased.
Thus, it means the value of y-intercept is $60.
We are told that Game tokens can be purchased by members at the reduced rate of $1.00 per 10 tokens. This means;
y/x = 1/10
Thus, slope = 1/10
Now, writing the equation of this function in slope intercept form gives;
y = (1/10)x + 60
Now, the number of game tokens purchased cannot be less than 0. Thus;
Domain; x ≤ 0
Since x ≤ 0, then the cost can't be less than $60.
Thus; Range; y ≥ 60
Read more at; https://brainly.com/question/20838649
then use your function to find the two roots. display ""x1"" and ""x2""
Answers
the two roots of the equation are x1 = -2.5 and x2 = -1.5.
x1 = -2.5;
x2 = -1.5.
Step 1: Calculate the discriminant
b2 - 4ac = (-2)2 - 4(2)(-3) = 4 + 24 = 28
Step 2: Calculate the roots
x1 = (-b + √D) / 2a = (-(-2) + √28) / 4 = (-2 + 5.29) / 4 = -2.5
x2 = (-b - √D) / 2a = (-(-2) - √28) / 4 = (-2 - 5.29) / 4 = -1.5
We start by calculating the discriminant, which is b2 - 4ac. In this case we have b2 = (-2)2 = 4 and ac = 2(-3) = -6, so the discriminant is 4 + 24 = 28. Then we calculate the two roots, x1 and x2, using the formula x1 = (-b + √D) / 2a and x2 = (-b - √D) / 2a. Substituting in the values we have, x1 = (-(-2) + √28) / 4 = (-2 + 5.29) / 4 = -2.5 and x2 = (-(-2) - √28) / 4 = (-2 - 5.29) / 4 = -1.5. Therefore, the two roots of the equation are x1 = -2.5 and x2 = -1.5.
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
Find the minimum value of the function f(x)=2x^2-9.1x+6
Answers
The function has a minimum of -4.35125
How to determine the minimum value of the function?From the question, the equation of tis given as
f(x)=2x^2-9.1x+6
Rewrite the function as follows
f(x) = 2x² -9.1x + 6
Next, we differentiate the function
This is represented as
f'(x) = 2 * 2x - 1 * 9.1 + 0 * 6
Evaluate
f'(x) = 4x - 9.1
Set the differentiated function to 0
This is represented as
f'(x) = 0
So, we have
4x - 9.1 = 0
This gives
4x = 9.1
Divide by 4
x = 2.275
Substitute x = 2.275 in f(x) = 2x² -9.1x + 6
f(2.275) = 2(2.275)² - 9.1(2.275) + 6
Evaluate
f(2.275) = -4.35125
Hence, the minimum is -4.35125
Read more about minimum vertex at
https://brainly.com/question/12125609
#SPJ1
solve for b (exact values) i got 2 sqrt 3 / 3 = b but i’m not sure if it’s right :(

Answers
Answer:
tan30°= opp÷adj = b÷1/2 =0.577=b÷0.5 then, b=0.2885
what is 3422.4 divided by 544
Answers
6.29117647059
This is the answer
Answer: 6.29117647059
Step-by-step explanation:
divide the problem :)
Can I get help please

Answers
The amount of money that I will have at the end of 20 years would be =$4,480. That is option D
What is compound interest?Compound interest is defined as the interest that is being earned on an account which is based on the rate and the time the investment was made.
The total amount invested (p)= $2,000
The rate of investment (r) = 5%
The time of investment(t)= 12 year
The compound interest warm from that account;
= P×T×R/100.
= 2,000×12×5/100
= 120000/100
= $1200
For the next 8 years with the rate of 8% ;
= 2,000×8×8/100
= 128000/100
= $1280
The total compound interest = $1200+$1280= $2,480
Therefore, the amount of money that I will have at the end of 10 years would be = 2000+2480 = $4,480
Learn more about simple interest here:
https://brainly.com/question/25793394
#SPJ1
solve it clearly!
Prove that if a sequenca (Cn)}o of integers satisfies = G(0) G(n) 0, n - G(G(n)) = (n = 1,2,3,...), then (a) G(k) > Gk – 1) for any positive integer k; (b) no integer k exists such that G(k – 1) =
Answers
To prove the given statements, let's analyze each part separately: (a) To prove that G(k) > G(k-1) for any positive integer k, we can use mathematical induction.
Base case: For k = 1, we have G(1) > G(0). This is given in the sequence condition. Inductive step: Assume that G(k) > G(k-1) for some positive integer k.
Now, we need to show that G(k+1) > G(k). Using the sequence condition, we have:
G(G(k)) > G(k) (1)
Since G(k) > G(k-1) (by the assumption), we can substitute it into equation (1):
G(G(k)) > G(k) > G(k-1)
Now, let's consider the condition n - G(G(n)) = 0:
G(G(n)) < n
Substituting k+1 for n:
G(G(k+1)) < k+1
Combining the above inequalities, we get:
G(G(k)) > G(k) > G(k-1) > G(G(k+1))
Therefore, G(k+1) > G(k), which completes the inductive step.
By the principle of mathematical induction, we can conclude that G(k) > G(k-1) for any positive integer k.
(b) To prove that no integer k exists such that G(k-1) = k, we can use contradiction.
Assume that there exists an integer k such that G(k-1) = k. Then, according to the given sequence condition, we have:
k - G(G(k)) = 0
Substituting G(k-1) = k:
k - G(G(k-1)) = 0
Since G(G(k-1)) = G(k), we have:
k - G(k) = 0
However, this contradicts the condition that G(k) > G(k-1) for any positive integer k (as proven in part (a)). Therefore, no integer k exists such that G(k-1) = k.
Hence, we have proved both statements (a) and (b).
Learn more about integer here
https://brainly.com/question/929808
#SPJ11
Write an equation to model the situation: A girl and another girl are baking
cookies. One bakes 5 more than 3 times as many cookies as the other.
Together they bake 150 cookies.
Answers
Answer:
3x + 5 = 150
Step-by-step explanation:
3x + 5 represents 3 times as many cookies plus 5 and 150 represents the total amount of cookies.
In further detail, x represents how many cookies the other girl baked.
Apples cost $0.95 per pound and bananas cost $1.10 per pound.
Leah bought a total of 8 pounds of apples and bananas for $8.05.
a+b=8
The system of equations
models this
0.95a + 1.10b = 8.05
situation, where a is the number of pounds of apples and b is
the number of pounds of bananas. How many pounds of each did
Leah buy?
1

Answers
Answer:
I think the answer would be 3.92682926829
Step-by-step explanation:
Honestly i dont think i did this right at all. But i hope i did.
Here is what i did:
0.95 + 1.10 = 2.05
8.05 divided by 2.05 = 3.92682926829
Im so sorry if you get this wrong. I honestly am having an off day. Good luck :(
Billy likes to go cycling.
His bike has wheels of diameter 80 cm.
He has a counter on his bike which
counts the number of revolutions
the wheels make.
One day the counter shows 350 revolutions.
How far has Billy cycled?
Give your answer to the nearest metre.
Answers
Answer:
560 metres
Step-by-step explanation:
80 cm in metres is 0.8 metres.
After 1 revolution any point on the wheel will be back to the original position before moving. 0.8 times 2, which gives us 1.6 metres. In 1 revolution the bike travels 1.6 metres.
Now 1.6 metres times 350 gives us 560.
So the answer is 560 metres.
in three flips of an unfair coin the probability of getting three heads is the same as the probability of getting exactly two tails. what is the ratio of the probability of flipping a tail to the probability of flipping a head?
Answers
The ratio of the probability of flipping a tail to the probability of flipping a head when the probability of getting three heads is the same as the probability of getting exactly two tails in three flips is 1/3.
How to find the ratio of probability of flipping a tail to probability of flipping a head?Let p be the probability of flipping a head and q be the probability of flipping a tail.
The probability of getting three heads in three flips is \((p)^3.\)
The probability of getting exactly two tails in three flips is 3pq².
Given that these probabilities are equal, we have:
\((p)^3\)= 3pq²
Simplifying this equation gives:
p = 3q
Dividing both sides by q gives:
p/q = 3
Therefore, the ratio of the probability of flipping a tail to the probability of flipping a head is 1/3.
Learn more about Probability
brainly.com/question/30034780
#SPJ11
To save money for prom this weekend, Tom is going to walk his neighbor's dog for $6 per hour and wash cars for $7.50 per hour. His mother sid he can work no more than 15 hours to ensure he keeps up with his homework. Tom needs to make at least $75 to cover prom expenses. If d represents the number of hours walking his neighbor's dog and c represents the number of hours washing cars, which system of inequalities represents this situation?
a
\large 6d+7.5c\le15
\large d+c\ge75
b
\large 6d+7.5c\le75
\large d+c\ge15
c
\large 6d+7.5c\ge75
\large d+c\le15
d
\large 6d+7.5c\ge15
\large d+c\le75
Answers
Answer:
d + c ≤ 15
6*d + 7.50*c≥ 75
Step-by-step explanation:
Mathematical inequality is that proposition that relates two algebraic expressions whose values are different. It is a proposition of relation between two different elements, either by greater, lesser, greater or equal inequality, or less or equal.
In other words, an inequality is obtained by writing two numerical or algebraic expressions related to any of the symbols>, <, ≥ or ≤.
You know Tom's mom said that he can't work more than 15 hours to make sure he keeps up with his homework. That is, the number of hours walking the neighbor's dog added to the car wash should not exceed 15 hours, that is, it must be less than or equal to that amount. If d represents the number of hours walking your neighbor's dog and c represents the number of hours washing cars, then it is possible to represent this by the following inequality:
d + c ≤ 15 Inequality (A)
On the other hand, you know that Tom needs to earn at least $ 75 to cover the expenses of this weekend's prom. In other words, the money earned by walking dogs added to that earned by washing cars must be equal to or greater than $ 75. If Tom will walk his neighbor's dog for $ 6 an hour and wash cars for $ 7.50 an hour, then $ 6*d is the money earned walking dogs and $ 7.50*c is the money earned from washing cars. So this is represented by the inequality:
6*d + 7.50*c≥ 75 Inequality (B)
Then the system of inequalities that represents this situation is given by the Inequation (A) and the Inequation (B)
which of the following series satisfy the given condition. the series is geometric with x = 1/3.
Answers
The answer is Series 1. It satisfies the given condition as it is a geometric series with a common ratio of 1/3. Each term in this series is obtained by multiplying the previous term by 1/3, which confirms that it is indeed a geometric series with the given condition.
We need to test each series to see if it is geometric with x = 1/3. Remember, a geometric series is one in which each term is obtained by multiplying the previous term by a constant value. In this case, that constant value is x = 1/3. Let's test three series to see if they fit the given condition: 1) 3, 1, 1/3, 1/9, 1/27, ...
To see if this series is geometric with x = 1/3, we can check if each term is obtained by multiplying the previous term by 1/3.
1/3 ÷ 1 = 1/3
1/9 ÷ 1/3 = 1/3
1/27 ÷ 1/9 = 1/3
Since each term is obtained by multiplying the previous term by 1/3, this series is geometric with x = 1/3.
2) 1, 1/3, 3, 1/9, 9, ...
To test if this series is geometric with x = 1/3, we can check if each term is obtained by multiplying the previous term by 1/3.
1/3 ÷ 1 = 1/3
3 ÷ 1/3 = 9
1/9 ÷ 3 = 1/27
Since the terms are not consistently obtained by multiplying the previous term by 1/3, this series is not geometric with x = 1/3.
3) 1, 1/3, 1/9, 1/27, ...
To test if this series is geometric with x = 1/3, we can check if each term is obtained by multiplying the previous term by 1/3.
1/3 ÷ 1 = 1/3
1/9 ÷ 1/3 = 1/3
1/27 ÷ 1/9 = 1/3
Since each term is obtained by multiplying the previous term by 1/3, this series is geometric with x = 1/3.
To know more about geometric visit :-
https://brainly.com/question/12500691
#SPJ11
Marc doesn’t think that the angle of the front seat in his mom’s car is very cool, so he tilts the seat back. If m∠XWZ=115° and m∠YWX=15°, find m∠YWX

Answers
The defect rate for your product has historically been about 2.00% For a sample size of 400, the upper and lower 3-sigma control chart limits are:
UCLp = (enter your response as a number between 0 and 1, rounded to four decimal places).
LCL Subscript p=
Answers
The p-chart is used to monitor the proportion of defective items in a sample.
How would you interpret the upper and lower control limits on a p-chart?The upper and lower 3-sigma control chart limits for a defect rate, we need to use the p-chart formula.
The p-chart is used to monitor the proportion of defective items in a sample. Given a historical defect rate of 2.00% (0.02) and a sample size of 400, we can calculate the control limits.
The formula for the control limits is:
UCLp = p + 3 * sqrt((p * (1 - p)) / n)
LCLp = p - 3 * sqrt((p * (1 - p)) / n)
Substituting the values, we get:
UCLp = 0.02 + 3 * sqrt((0.02 * (1 - 0.02)) / 400) ≈ 0.0263
LCLp = 0.02 - 3 * sqrt((0.02 * (1 - 0.02)) / 400) ≈ 0.0137
The upper control limit (UCLp) is approximately 0.0263, and the lower control limit (LCLp) is approximately 0.0137.
Learn more about p-chart
brainly.com/question/31797771
#SPJ11
you need gi wrap a Christmas present for your friend. the box the gift is in has a length of 12 inches, a width of 8 inches, and a height of 7 inches how much wrapping paper do we need

Answers
The given problem can be exemplified in the following diagram:
The amount of paper needed to wrap the box is equivalent to the surface area of the box.. the surface area is equivalent to the sum of the areas of each face. Therefore, the surface area is:
\(A=2(12)(7)+2(8)(7)+2(12)(8)\)Each term is multiplied by two representing the two faces of the corresponding area:
Solving the operations:
\(A=472\)Therefore, 472 square inches of wrapping paper is needed.

The inverse of a conditional statement is "If a number is negative, then it has a negative cube root."
What is the contrapositive of the original conditional statement?
If a number is negative, then it does not have a negative cube root.
O If a number does not have a negative cube root, then the number is not negative.
O If a number has a negative cube root, then the number is negative.
O If a number is not negative, then it does not have a negative cube root.

Answers
Answer:
C. If a number has a negative cube root, then the number is negative.
Step-by-step explanation:
took the quiz
The inverse of the conditional statement is " If a number does not have a negative cube root, then the number is not negative. "
What is a conditional statement?A conditional statement is a type of logical statement that expresses a relationship between two propositions or statements. It typically takes the form "if p, then q" where p and q are propositions. The statement "if p, then q" is read as "if p is true, then q is true" or "p implies q".
The truth value of a conditional statement depends on the truth values of its antecedent (p) and its consequent (q). If p is true and q is true, then the conditional statement is true. If p is true and q is false, then the conditional statement is false. If p is false, then the truth value of the conditional statement is irrelevant and it is said to be vacuously true.
Given data ,
Let the statement be represented as A
Now , the inverse of the statement is A'
where A = "If a number is negative, then it has a negative cube root."
Now , the inverse of the conditional statement is
A' = " If a number does not have a negative cube root, then the number is not negative. "
Hence , the inverse is " If a number does not have a negative cube root, then the number is not negative. "
To learn more about conditional statements click :
https://brainly.com/question/18152035
#SPJ7
A water park has pools, slides, and rides that, in total, make use of 7.7 × 1 0 5 7.7×10 to the power of 5 gallons of water. They plan to add a ride that would make use of an additional 6.3 × 1 0 5 6.3×10 to the power of 5 gallons of water. Use scientific notation to express the total gallons of water made use of in the park after the new ride is installed.
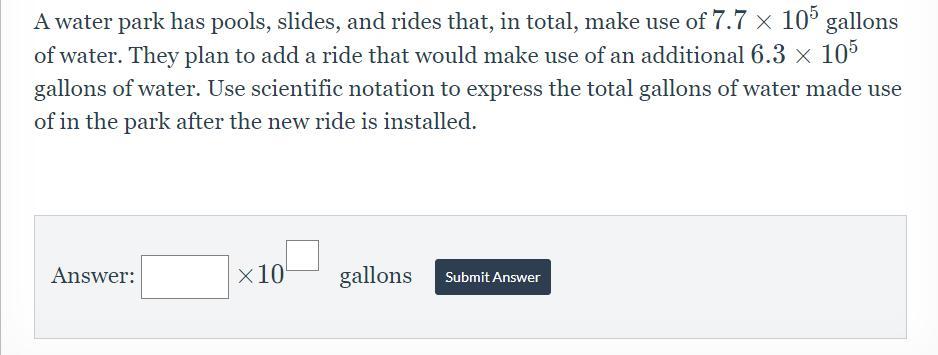
Answers
On solving the provided question, we can say that As a result, the total expression number of gallons of water used at the park when the new ride is placed is 1.4 106 gallons.
What is expression ?An expression in mathematics is a collection of representations, numbers, and conglomerates that mimic a statistical correlation or regularity. A real number, a mutable, or a mix of the two can be used as an expression. Mathematical operators include addition, subtraction, fast spread, division, and exponentiation. Expressions are often used in arithmetic, mathematics, and form. They are employed in the depiction of mathematical formulas, the solving of equations, and the simplification of mathematical relationships.
To calculate the total gallons of water used at the park once the new ride is constructed, add the amount of water used by the current pools, slides, and rides to the amount of water needed by the new ride. In scientific notation, we may represent water consumption as follows:
Total water consumption = \((7.7105) + (6.3105) = 14.105\).
Alternatively, we may simplify this by by translating 14 to scientific notation:
Total water consumption = \(1.41011105 = 1.4106\)
As a result, the total number of gallons of water used at the park when the new ride is placed is 1.4106 gallons.
To know more about scientific notation, visit
brainly.com/question/18073768
#SPJ1
Which option for college funding can parents start when children are still very young? College savings account scholarship work-study student loan
Answers
Answer:
Your answer would be A: "college savings account."
Step-by-step explanation:
Got it right on edge.
College savings account is the option for college funding can parents start when children are still very young
What is College funding?College financial aid pays for the difference between what a school costs to attend and the amount a family will pay from their own money.
We need to find Which option for college funding can parents start when children are still very young.
Among the two options we have to choose College savings account.
Through this savings plan, you can contribute more than a traditional savings plan and take out the money to pay for college-related expenses without any penalty or tax.
Hence College savings account option for college funding can parents start when children are still very young
To learn more on College funding click:
https://brainly.com/question/18614442
#SPJ6
find the limit. (if an answer does not exist, enter dne.) lim x → 0 tan−1(ln(x))
Answers
The answer doesn't exist for lim x → 0 tan−1(ln(x)).
To find the limit of the function as x approaches 0, lim(x→0) arctan(ln(x)), we need to analyze the behavior of the function near x = 0.
1. Consider the domain of the function. The natural logarithm ln(x) is only defined for x > 0, so we cannot evaluate the function at x = 0. However, we can still analyze the limit as x approaches 0 from the right.
2. As x approaches 0 from the right (x → 0+), the natural logarithm ln(x) approaches negative infinity (ln(x) → -∞).
3. The arctan function is continuous and has horizontal asymptotes at y = -π/2 and y = π/2. When its argument approaches negative infinity (ln(x) → -∞), the arctan function approaches its horizontal asymptote at y = -π/2.
Therefore, the limit of the function as x approaches 0 from the right is -π/2: lim(x→0+) arctan(ln(x)) = -π/2.
Since the function is not defined for x ≤ 0, the limit as x approaches 0 does not exist. Your answer is DNE (does not exist).
To learn more about limit: https://brainly.com/question/30679261
#SPJ11
An experiment consists of rolling two fair number cubes. The diagram shows the sample space of all equally likely outcomes. Find P(1 and 2). Express your answer as a fraction in simplest form.
Answers
Since the sample space contains \(36\) equally likely outcomes, each outcome has a probability of \(1/36\)
What is the probability?The sample space consists of all possible outcomes when rolling two number cubes. Each cube has six equally likely outcomes, so the total number of outcomes is\(6\times6=36.\)
P(1 and 2) refers to the probability of rolling a 1 on the first cube and a 2 on the second cube. There is only one outcome that satisfies this condition, which is \((1, 2)\) .
Therefore, the probability of rolling a 1 and 2 is:
P(1 and 2) = (number of outcomes that satisfy the condition)/(total number of possible outcomes)
P(1 and 2) \(= 1/36\)
Therefore, the probability of rolling a \(1\) and \(2\) is \(1/36\) .
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ1
Answer:
Since the sample space contains 36 equally likely outcomes, each outcome has a probability of 1 / 36.
We know that probability is defined as number of favourable outcomes divided by total number of outcomes.
Step-by-step explanation:
An experiment occurs of rolling two fair number cubes.
We have given number of favourable outcomes = 2 {(2,1), (1,2)}
Number of Total Outcomes = 36
So ,
Probability = Number of favourable outcomes / Total Outcomes
P(1 and 2) refers to the probability of rolling a 1 on the first cube and a 2 on the second cube. There is only one outcome that satisfies this condition, which is (1, 2).
P(1 and 2) = 2 / 36
P(1 and 2) = 1 / 18
Hence , 1 / 18 is the answer as a fraction in simplest form.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ1
3(a+5) -2(a+a) explain step by step
Answers
Answer:
-a + 15
General Formulas and Concepts:
Pre-Algebra
Distributive PropertyAlgebra I
Combining Like TermsStep-by-step explanation:
Step 1: Define
3(a + 5) - 2(a + a)
Step 2: Simplify
Combine like terms: 3(a + 5) - 2(2a)Distribute 3: 3a + 15 - 2(2a)Multiply: 3a + 15 - 4aCombine like terms: -a + 15Maple Trail intersects Woodland Trail and elm trail at their midpoint. you enter the trails at point P. you walk from the entrance up woodland trail to maple trail, over maple trail to elm trail, down elm trail to oak trail, and then back to the entrance. how many miles did you walk?
Answers
Answer: 5 Miles
Step-by-step explanation:
Big ideas
PLEASE HELP FAST ILL GIVE BRAINLIEST IF CORRECT!!!!
The two lines graphed below are not parallel. How many solutions are there to the system of equations?
A. One solution
B. Infinitely many solutions
C. Two solutions
D. No solutions

Answers
Answer: (A) One solution
the null hypothesis for the single factor anova states that all means are equal.
T/F
Answers
The null hypothesis for the single factor ANOVA states that all means are equally true.
The null hypothesis for a single-factor ANOVA (analysis of variance) states that all means are equal.
The alternative hypothesis, on the other hand, suggests that at least one of the means is different from the others.
The purpose of the ANOVA test is to determine whether there is sufficient evidence to reject the null hypothesis and conclude that there are significant differences between the means. A statistical formula used to compare variances across the means (or average) of different groups.
Hence, the statement is true .
To know more about null hypothesis click here :
https://brainly.com/question/30821298
#SPJ4
D
.0
A
58d
B
A, B, C and D are points on a circle, centre O.
Angle ABC = 58°
Calculate the size of angle ADC.
(1 mark)
Diagram NOT
accurately drawn

Answers
Answer:
∠ ADC = 122°
Step-by-step explanation:
ABCD is a cyclic quadrilateral.
opposite angles in a cyclic quadrilateral sum to 180° , that is
∠ ADC + ∠ ABC = 180∠
∠ ADC + 58° = 180° ( subtract 58° from both sides )
∠ ADC = 122°
Diana is painting statues. She has 7/8 of a liter of paint remaining. Each statue requires 1/20 of a liter of paint. How many statues can she paint?
Answers
Answer:
She can paint 17 statues
Step-by-step explanation:
Sorry I don’t really know how to show my work
Answer:
140/8
simplified: 35/2
decimal: 17.5
Step-by-step explanation:
honestly, I don't know how to show my work but I hope this helps.

Find the greatest common factor of 10,30, and 45
Answers
Answer:
30
Step-by-step explanation: