7) when constructing a confidence interval for the population mean when the standard deviation is unknown, what is the formula for standard error?
Answers
When constructing a confidence interval for the population mean when the standard deviation is unknown, the formula for standard error is: s/√n, where s is the sample standard deviation and n is the sample size.
Begin with a sample: Start with a sample of size n that is representative of the population of interest. The sample is used to estimate the population mean.
Compute the sample standard deviation: Calculate the sample standard deviation, denoted as s, which measures the variability or spread of the sample data. The sample standard deviation is an estimate of the population standard deviation.
Calculate the standard error: The standard error represents the standard deviation of the sampling distribution of the sample mean. It quantifies the variability or uncertainty associated with estimating the population mean based on the sample.
The formula for the standard error is: Standard Error = s / √n
s: Sample standard deviation, which measures the variability of the sample data.
n: Sample size, the number of observations in the sample.
Standard Error = Sample Standard Deviation / √(Sample Size)
By dividing the sample standard deviation by the square root of the sample size, we obtain the standard error.
Interpretation: The standard error gives us an idea of how much the sample means are likely to vary from the true population mean. Smaller standard errors indicate less variability and greater precision in estimating the population mean.
Confidence interval: Once the standard error is calculated, it is used along with the desired level of confidence and critical values from the appropriate distribution (such as the t-distribution or the standard normal distribution) to construct a confidence interval for the population mean.
The confidence interval represents a range of values within which we can be confident, with a specified level of confidence, that the true population mean lies.
To summarize, when constructing a confidence interval for the population mean when the standard deviation is unknown, we calculate the standard error by dividing the sample standard deviation by the square root of the sample size.
Know more about the standard error click here:
https://brainly.com/question/31941158
#SPJ11
Related Questions
1 1/9 x 3 5/10
Please educate me this basic knowledge because I’m so stupif
Answers
10/9 * 35/10 = 350/ 90
35/9 = 3.89
suppose that a family has 4 children.? also, suppose that the probability of having a girl is one half. find the probability that the family has no more than 3 boys.
Answers
The probability that a family with 4 children has no more than 3 boys is 15/16.
To find the probability that a family with 4 children has no more than 3 boys, we can use the binomial distribution.
The binomial distribution is used to calculate the probability of obtaining a certain number of successes (boys in this case) in a fixed number of trials (children in this case), where each trial has only two possible outcomes (boy or girl) and the trials are independent.
Let X be the number of boys in the family. We want to find P(X ≤ 3), which is the probability of having no more than 3 boys. Since the probability of having a boy is 1/2 and the trials are independent, we can use the binomial distribution formula:
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= (1/2)⁴ + 4(1/2)⁴ + 6(1/2)⁴ + 4(1/2)⁴
= 15/16
To learn more about probability click on,
https://brainly.com/question/29973811
#SPJ4
30 people travelled from London to Manchester for a conference. Of these people 15 travelled by train 9 travelled by plane some travelled by both train and plane 12 did not travel by either train or plane Three people are chosen at random from those who travelled by plane. Find the probability that exactly two of these people also travelled by train.
Answers
The probability that exactly two of the three people selected also travel by train is 4/9
What is the probability of an event occurring?The probability of an event occurring is specified by the ratio of the number of required outcomes to the number of possible outcomes.
The number of people that travelled from London to Manchester for the conference = 30
Number of people that traveled by train = 15
Number of people that travelled by plane = 9
Number of people that did not travel by travel by either train or plane = 12
Number of people chosen from those that traveled by plane = 3
The probability that two of those selected also traveled by train can be found as follows;
The number of people that traveled by either train of plane = 30 - 12 = 18
The number of people that traveled by plane and train = 15 + 9 - 18 = 6
The binomial probability distribution formula that can be used to find the probability of an event, p, occurring exactly r times is as follows;
P(p) = \(_nC_r\cdot p^r\cdot q^{n-r}\)
Where;
n = Number of people chosen = 3
r = Number of people chosen that also traveled by train = 2
p = Probability that a person chosen also traveled by train = 6/9 = 2/3
q = Probability that a person chosen did not travel by train = 3/9 = 1/3
Therefore;
\(P = _3C_2\times \left(\dfrac{2}{3}\right) ^2\times \left(\dfrac{1}{3} \right)^{3-2} = \dfrac{4}{9}\)
The probability that exactly two of the people chosen at random also traveled by train is P = 4/9Learn more about the probability of an event here:
https://brainly.com/question/16237647
#SPJ1
A population of 350 animals has a growth rate of 5% each year. Write a exponential function to model the situation.
Answers
Answer: A =350 (1.05)^t
Step-by-step explanation:
Hi, to answer this question we have to apply an exponential growth function:
A = P (1 + r) t
Where:
p = original population
r = growing rate (decimal form; 5/100=0.05)
t= years
A = population after t years
Replacing with the values given:
A = 350 (1+0.05)^t
A =350 (1.05)^t
Feel free to ask for more if needed or if you did not understand something.
I will mark brainliest!!
Create the equation of a quadratic function with a vertex of (-3, 7)
and a y-intercept of -2.
Answers
Answer:
m a th wa y
Step-by-step explanation:
I NEED THIS ANSWER BY TONIGHT BY 9:00 PLEASE HELP!!
Which number sentence has exactly one solution A. x+5.4>8 B. 1/4 (x-5)=13 C. 3x+7.5<9 D. 1/2x-19>24
Answers
Answer:
B. 1/4(x-5) = 13
Step-by-step explanation:
You want to know which number sentence has one solution.
InequalityTypically, an inequality has an infinite set of solutions. The inequalities here are linear inequalities in one variable, so will have an infinite solution set consisting of numbers greater than, or less than, some boundary value.
EquationIf the equation can be arranged to be in general form, ax +b = 0, where a ≠ 0, then it will have exactly one solution: x = -b/a.
The set of number sentences contains exactly one equation. That is the number sentence that has exactly one solution:
B. 1/4(x-5) = 13
En cierto cultivo, inicialmente había 1000 amebas que se reproducen por biparticion cada día ¿Cuántas amebas habrá al cabo de 30 días después que se inició el cultivo ?
Answers
Answer: 1,073,741,824,000 amebas
Step-by-step explanation:
Bipartición significa que la población de amebas se duplica cada día.
Entonces si inicialmente hay 1000, después de un día van a haber:
2*1000.
Después del segundo día se vuelven a duplicar, entonces van a haber:
2*(2*1000) = (2^2)*1000
Después del tercer día, lo mismo:
2*(2^2)*1000 = (2^3)*1000.
A esta altura ya se puede ver el patrón, podemos concluir que después de N días, la población de amebas va a ser:
P(N) = (2^N)*1000.
Entonces respondiendo a la pregunta:
¿Cuántas amebas habrá al cabo de 30 días después que se inició el cultivo?
Tenemos que tomar N = 30
P(30) = (2^30)*1000 = 1,073,741,824,000 amebas
Este gráfico circular resume las especializaciones de los 450 miembros de una sororidad universitaria. El ángulo central el sector correspondiente a la especialización de ingeniería mide 50.4°. ¿Qué porcentaje de los miembros de la sororidad se especializan en ingeniería? No redondear.
Answers
Los miembros de la sororidad tiene un porcentaje de 14 % de estudiantes procedentes de la especialización de ingeniería.
¿Cuál es el porcentaje de estudiantes de la sororidad que pertenecen a la especialización de ingeniería?
El enunciado describe las características de un diagrama circula, en donde el 100 % de los miembros de la sororidad representan a los 360° del ángulo central del círculo, esto es, una revolución completa del círculo.
El porcentaje de los miembros que se especializan en ingeniería mediante la siguiente fórmula:
e = (E / 360°) × 100 %
Donde E es el ángulo asociado a la cantidad de estudiantes de la especialización de ingeniería, en grados sexagesimales.
e = (50.4° / 360°) × 100 %
e = 14 %
Los estudiantes que especializan en ingeniería corresponden a un porcentaje de 14 % de los miembros de la sororidad.
Para aprender más sobre porcentajes: https://brainly.com/question/10114228
#SPJ1
the population in a small us city has been increasing linearly. in 2014, the population of this town was 29,333. by the year 2019, it grew to 35,203. the function/model/equations is:
Answers
If the population grew to 35203 by the year 2019 , then the equation to model this situation is y = 1174x + 29333 .
We use the given data points to create a linear equation to model the population growth over the years.
Let , x₁ = 0 represents the year 2014
⇒ y₁ = 29333 represents the population in the year 2014
⇒ x₂ = 5 represents the year 2019
⇒ y₂ = 35203 represents the population in the year 2019
Using these variables, we can find the slope of the line that represents the population growth:
So , slope = (y₂ - y₁)/(x₂ - x₁)
⇒ slope = (35203 - 29333)/(5 - 0) ;
⇒ slope = 5870/5 = 1174 ;
Now , by using the point-slope form of a linear equation
we get ;
⇒ y - y₁ = m(x - x₁) ;
⇒ y - 29333 = 1174(x - 0) ;
Simplifying this equation ;
we get ;
⇒ y = 1174x + 29333 ;
Therefore, the equation for the model is y = 1174x + 29333, where y represents the population and x represents the number of years since 2014.
Learn more about Equation here
https://brainly.com/question/9630347
#SPJ4
The given question is incomplete , the complete question is
The population in a small us city has been increasing linearly. in 2014, the population of this town was 29333. and by the year 2019, it grew to 35,203. Find the equation for this model ?
A particle is moving with the given data. Find the position of the particle.
a(t) = 2t + 9, s(0) = 8, v(0) = −4
Answers
To find the position of the particle, we need to integrate the acceleration function twice with respect to time, starting from the initial conditions of position and velocity.
Given:
a(t) = 2t + 9 (acceleration function)
s(0) = 8 (initial position)
v(0) = -4 (initial velocity)
First, let's integrate the acceleration function to find the velocity function:
v(t) = ∫(2t + 9) dt
= t^2 + 9t + C1
Using the initial velocity condition, we can solve for the constant C1:
v(0) = 0^2 + 9(0) + C1 = -4
C1 = -4
Therefore, the velocity function becomes:
v(t) = t^2 + 9t - 4
Next, we integrate the velocity function to find the position function:
s(t) = ∫(t^2 + 9t - 4) dt
= (1/3)t^3 + (9/2)t^2 - 4t + C2
Using the initial position condition, we can solve for the constant C2:
s(0) = (1/3)(0^3) + (9/2)(0^2) - 4(0) + C2 = 8
C2 = 8
Therefore, the position function becomes:
s(t) = (1/3)t^3 + (9/2)t^2 - 4t + 8
Thus, the position of the particle is given by the function s(t) = (1/3)t^3 + (9/2)t^2 - 4t + 8.
To know more about acceleration refer here
https://brainly.com/question/2303856#
#SPJ11
The percentage of people of any particular age group that will die in a given year may be approximated by the formula P(t) 0.00236 e0 53t where t is the age of the person in years a. Find P(25). P(50), and P(75) b. Find P'(25), P' (50), and P (75). c. Interpret your answers for parts a and b. Are there any limitations of this formula? a. P/25) Round to three decimal places as needed.) P(50) Round to three decimal places as needed.) P75)- Round to three decimal places as needed.) b, P'(25) Round to four decimal places as needed.) P(50) Round to four decimal places as needed.) P(75) c. Choose the correct answer below O A The percentage of people ın each of he age groups that die in a given year is creasing The ormula implies hat even one will be dead by age 11 O B. The percentage of people in each of the age groups that die in a given year is decreasing. There are no limitations of this formula. O C. The percentage of people in each of the age groups that die in a given year is increasing. There are no limitations of this formula O D. The percentage of people in each of the age groups that die in a given year is decreasing The formula implies that everyone will be dead by age 120
Answers
The percentage of people in each of the age groups that die in a given year is creasing The formula implies that even one will be dead by age 112.
What is the exponential function?
Although the exponential function was derived from the concept of exponentiation (repeated multiplication), contemporary formulations (there are numerous comparable characterizations) allow it to be rigorously extended to all real arguments, including irrational values.
Here, we have
Given: The percentage of people of any particular age group that will die in a given year may be approximated by the formula
P(t) = 0.00236 \(e^{0.0953t}\)....(1)
(a) We have to find the value of P(25).
When t = 25
Now we put the value of t in equation (1) and we get
P(25) = 0.00236 \(e^{0.0953(25)}\)
= 0.02556
P(25) = 0.026
We have to find the value of P(50).
When t = 50
Now we put the value of t in equation (1) and we get
P(50) = 0.00236 \(e^{0.0953(50)}\)
P(50) = 0.277
We have to find the value of P(75).
When t = 75
Now we put the value of t in equation (1) and we get
P(75) = 0.00236 \(e^{0.0953(75)}\)
P(75) = 2.999
(b) We have to find the value of P'(25)
When we differentiate equation (1) and we get
P'(t) = 0.00236×0.0953\(e^{0.0953t}\)....(2)
When t = 25
Now we put the value of t in equation (2) and we get
P'(25) = 0.00236×0.0953\(e^{0.0953(25)}\)
P'(25) = 0.0024
We have to find the value of P'(50)
When t = 50
Now we put the value of t in equation (2) and we get
P'(50) = 0.00236×0.0953\(e^{0.095350)}\)
P'(50) = 0.026
We have to find the value of P'(75)
When t = 75
Now we put the value of t in equation (2) and we get
P'(75) = 0.00236×0.0953\(e^{0.0953(75)}\)
P'(75) = 0.286
(c) Let P(t) = 100
100 = 0.00236 \(e^{0.0953t}\)
t = 112
Hence, The percentage of people in each of the age groups that die in a given year is creasing The formula implies that even one will be dead by age 112.
To learn more about the exponential function from the given link
https://brainly.com/question/2456547
#SPJ4
The formula suggests that even at age 112, there will be some mortality rate within the population.
The given formula, P(t) = 0.00236, represents the percentage of people in any particular age group who will die in a given year.
(a) To find the value of P(25), we substitute t = 25 into the equation:
P(25) = 0.00236
Therefore, P(25) = 0.00236 or approximately 0.026.
Similarly, for P(50):
P(50) = 0.00236 or approximately 0.277.
And for P(75):
P(75) = 0.00236 or approximately 2.999.
(b) To find the value of P'(25), we differentiate the equation P(t) = 0.00236:
P'(t) = 0.00236 × 0.0953
Substituting t = 25:
P'(25) = 0.00236 × 0.0953
Therefore, P'(25) = 0.0024.
Similarly, for P'(50):
P'(50) = 0.00236 × 0.0953 or approximately 0.026.
And for P'(75):
P'(75) = 0.00236 × 0.0953 or approximately 0.286.
(c) If we set P(t) = 100, we can solve for t:
100 = 0.00236
Solving for t, we find:
t = 112
This implies that according to the given formula, the percentage of people in each age group dying in a given year, even one person will be dead by the age of 112.
Therefore, the formula suggests that even at age 112, there will be some mortality rate within the population.
To learn more about the mortality rate from the given link
https://brainly.com/question/28488879
#SPJ11
a bucket at the bottom of a well is filled with water with a total weight of 3kg. the bucket is at the end of a 5m rope and the rope weighs 7kg in total. how much work is required to pull the bucket of water to the top of the well?
Answers
500 J, is the required work to pull the bucket of water to the top of the well.
From the given question we have the following information
the weight of the bucket is 3kg.
length of rope (h) = 5m
Weight of rope: 7kg
Total weight (rope + bucket) = 10kg
Required Work Done = force × distance travelled (length of rope ) = mgh, where
M = total weight in kg
g--> acceleration due to gravity
h--> length of rope ( height )
g = 10 m/sec² ( default value )
Put all the values in the above formula.
Required work done = 100× 5 = 500 Joules .
So, the bucket of water will require 500J work done for pulling.
To learn more about Work done, refer :
https://brainly.com/question/12026891
#SPJ4
The cost to ride a ferris wheel is $2.00 per person. The ferris a wheel has a capacity of
64 people. The amount of money collected is a function of the number of people who
ride on the ferris wheel.
M(p) = 2p
Use the drop-down menus to complete the statements below about the domain of this
function.
Answers
Answer:
When we have a function f(x), the domain of the function is the set of all the inputs that "work" (Not only in a mathematical way, the context is also important) with the function f(x)
In this case, we have a function M(p) = $2*p
This function represents the amount of money collected depending on the number of people who ride on the ferris whell.
Then p can be only a whole number (we can not have 1.5 people, only whole numbers of people).
And we also know that the maximum capacity of the ferris is 64 people.
Then:
p ≤ 64
And we also should add the restriction:
0 ≤ p ≤ 64
(Because p can't be smaller than zero)
Such that p should also be an integer, then, the domain is:
D: p ∈ Z, p ∈ {0, 1, 2, ..., 64}
Graph △RST with vertices R(4, 1), S(7, 3), and T(6, 4) and its image after the glide reflection.
Translation: (x, y)→(x, y−1)
Reflection: in the y-axis.
Answers
Graph △RST with vertices R(4, 1), S(7, 3), and T(6, 4) and its image after the glide reflection is shown in figure.
What is mean by Triangle?A triangle is a three sided polygon, which has three vertices and three angles which has the sum 180 degrees.
Given that;
In △RST;
The vertices are, R(4, 1), S(7, 3), and T(6, 4)
Here, Translation: (x, y) → (x, y−1)
And, Reflection in the y-axis.
Hence, New coordinate of the image of △RST are,
⇒ R' = (- 4, 1 - 1) = (- 4, 0)
⇒ S' = (- 7, 3- 1) = (- 7, 2)
⇒ T' = (- 6, 4 - 1) = (- 6, 3)
Thus, Graph △RST with vertices R(4, 1), S(7, 3), and T(6, 4) and its image after the glide reflection is shown in figure.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1

The rate at which rainwater flows into a drainpipe is modeled by the function R, where R(t)=20sin(t^2/35) cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
Answers
There are 30 cubic feet of water in the pipe at time t = 0. 76.570 cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8.
\(\int\limits^8_0\) [R(t) dt = \(\int\limits^8_0\) 20 sin \(\frac{t^2}{35}\) dt = 76.570
What Is Time Interval?
The amount of time between two given times is known as time interval. In other words, it is the amount of time that has passed between the beginning and end of the event. It is also known as elapsed time.
INTERVAL types are divided into two classes: year-month intervals and day-time intervals. A year-month interval can represent a span of years and months, and a day-time interval can represent a span of days, hours, minutes, seconds, and fractions of a second.
Learn more about time interval from brainly, visit: brainly.com/question/15848206
#SPJ4
describe the circumstances under which the shape of the sampling distribution of pn is approximately normal.
Answers
Main Answer:The circumstances under which the shape of the sampling distribution of pn is approximately normal.
Supporting Question and Answer:
What is the Central Limit Theorem and how does it relate to the shape of the sampling distribution of pn?
The Central Limit Theorem states that, under certain conditions, the sampling distribution of the sample mean (or sum) approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution. This theorem is applicable to the sampling distribution of pn (proportion) because the proportion can be considered as the sample mean of a binary variable (success or failure). As the sample size increases, the Central Limit Theorem ensures that the sampling distribution of pn becomes more approximately normal, making it a useful approximation for making inferences about the population proportion.
Body of the Solution:The shape of the sampling distribution of pn (proportion) is approximately normal under certain circumstances. These circumstances are related to the properties of the population being sampled and the sample size. Here are the key factors:
1.Large sample size: The sampling distribution of pn tends to become more approximately normal as the sample size increases. This is known as the Central Limit Theorem. As the sample size grows larger, the distribution of sample proportions approaches a normal distribution regardless of the shape of the population distribution.
2.Random sampling: The sample should be selected randomly from the population to ensure that each member of the population has an equal chance of being included in the sample. Random sampling helps to ensure that the sample is representative of the population.
3.Independence assumption: The sampled observations should be independent of each other. This means that the selection of one observation should not influence the selection or behavior of other observations. Independence is crucial to ensure that the sampling distribution accurately reflects the population distribution.
4.Adequate population size: If the population size is sufficiently large,
relative to the sample size, the shape of the sampling distribution of pn is approximately normal. In practice, if the population is at least 10 times larger than the sample size, this condition is considered to be met.
5.Binomial distribution approximation: The shape of the sampling distribution of pn is also approximately normal when the underlying population distribution follows a binomial distribution. The binomial distribution is characterized by a fixed number of trials and two possible outcomes (success or failure) for each trial.
Final Answer: These circumstances increase the likelihood of the sampling distribution of pn being approximately normal, it does not guarantee it in all cases. In practice, checking the normality of the sampling distribution can be done using statistical tests or graphical methods, such as a histogram or a normal probability plot.
To learn more about the Central Limit Theorem and how does it relate to the shape of the sampling distribution of pn from the given link
https://brainly.com/question/7897151
#SPJ4
The circumstances under which the shape of the sampling distribution of pn is approximately normal.
What is the Central Limit Theorem and how does it relate to the shape of the sampling distribution of pn?The Central Limit Theorem states that, under certain conditions, the sampling distribution of the sample mean (or sum) approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution. This theorem is applicable to the sampling distribution of pn (proportion) because the proportion can be considered as the sample mean of a binary variable (success or failure). As the sample size increases, the Central Limit Theorem ensures that the sampling distribution of pn becomes more approximately normal, making it a useful approximation for making inferences about the population proportion.
The shape of the sampling distribution of pn (proportion) is approximately normal under certain circumstances. These circumstances are related to the properties of the population being sampled and the sample size. Here are the key factors:
1.Large sample size: The sampling distribution of pn tends to become more approximately normal as the sample size increases. This is known as the Central Limit Theorem. As the sample size grows larger, the distribution of sample proportions approaches a normal distribution regardless of the shape of the population distribution.
2.Random sampling: The sample should be selected randomly from the population to ensure that each member of the population has an equal chance of being included in the sample. Random sampling helps to ensure that the sample is representative of the population.
3.Independence assumption: The sampled observations should be independent of each other. This means that the selection of one observation should not influence the selection or behavior of other observations. Independence is crucial to ensure that the sampling distribution accurately reflects the population distribution.
4.Adequate population size: If the population size is sufficiently large,
relative to the sample size, the shape of the sampling distribution of pn is approximately normal. In practice, if the population is at least 10 times larger than the sample size, this condition is considered to be met.
5.Binomial distribution approximation: The shape of the sampling distribution of pn is also approximately normal when the underlying population distribution follows a binomial distribution. The binomial distribution is characterized by a fixed number of trials and two possible outcomes (success or failure) for each trial.
These circumstances increase the likelihood of the sampling distribution of pn being approximately normal, it does not guarantee it in all cases. In practice, checking the normality of the sampling distribution can be done using statistical tests or graphical methods, such as a histogram or a normal probability plot.
To learn more about the Central Limit Theorem
brainly.com/question/7897151
#SPJ4
Tell whether a triangle can have sides with lengths 35, 50, and 10.
Answers
Answer:
NO
Step-by-step explanation:
We can know the answer by using the Pythagorean Theorem.
In a triangle with uneven sides, the longest side is called the hypotenuse. In this case, it is 50.
Using the theorem: a² + b² = c²
(Let's say c is the hypotenuse and a and b are the other sides)
10² + 35² = 50²
100 + 1225 = 2500
1325 ≠ 2500
So the answer is NO
Answer:
False
Step-by-step explanation:
HELPPPPPP ITS ABOUT EQUATIONSSSS HELPPPPP Explanation needed HELPPPPP PLEASEE THIS IS THE LAST QUESTION LEFTTTTTTT

Answers
Answer:
C. the average total cost for the first month of a gym membership
Step-by-step explanation:
x=1 is for month 1,
the value of y includes 1-month fee and one off payment, so this is the average total for the first month of membership
Answer:
It is the average total cost for the first month of a gym membership
Step-by-step explanation:
y = 34.99x+49
The 49 is the cost to join the gym and the 34.99 is the monthly cost
Let x =1 which is the cost after one month
It includes the cost to join and the 1st month membership
It is the average total cost for the first month of a gym membership
below is the spreadsheet model we looked at in this module for measuring exponential growth of an epidemic. predict the number of users of a new social network at a future date assuming similar exponential growth. how many users of the new service would we expect to have in seven and a half months?
Answers
The formula used is \($N(t) = N_0 e^{rt}$\). If a new social network has 1000 users currently and at growth rate of 10% per month, it can be predicted that there will be approximately 2452 users in seven and a half months assuming similar exponential growth.
In the formula used in the spreadsheet model for measuring exponential growth i.e. \($N(t) = N_0 e^{rt}$\)
N(t) is the number of cases at time t
N₀ is the initial number of cases
e is the mathematical constant approximately equal to 2.71828
r is the growth rate (expressed as a decimal)
To adapt this formula to predict the number of users of a new social network, we can replace the variables with the appropriate values. For example, if the new social network has 1000 users currently and is growing at a rate of 10% per month, we can write:
N(t) = 1000 x \(e^{rt}$\)
To find the predicted number of users in seven and a half months, we can substitute t = 7.5 into the equation and solve for N(7.5):
N(7.5) = 1000 x \(e^{rt}$\)
N(7.5) ≈ 2452.22
Therefore, we would expect to have approximately 2452 users on the new social network in seven and a half months if it continues to experience similar exponential growth.
Learn more about growth rate :
https://brainly.com/question/30764119
#SPJ4
The complete question is :
What is the formula used in the spreadsheet model discussed in this module for measuring exponential growth of an epidemic, and how can it be adapted to predict the number of users of a new social network at a future date assuming similar exponential growth? In particular, if the new social network has 1000 users currently and is growing at a rate of 10% per month, how many users would we expect to have in seven and a half months?
please help factorise 7ab+a
Answers
Answer:
= a(7b + 1)
Step-by-step explanation:
7ab + a
a(7b + 1).
What is the solution to the equation below? (Round your answer to two
decimal places.)
log₂ x = 4.3
A. x = 18.49
B. x=2.15
C. x = 8.60
D. x=19.70
Answers
Answer:
D
Step-by-step explanation:
using the rule of logarithms
\(log_{b}\) x = n ⇒ x = \(b^{n}\) , then
\(log_{2}\) x = 4.3 ⇒ x = \(2^{4.3}\) ≈ 19.70 ( to 2 dec. places )
HELP ASAP!! ILL MARK BRAINLIEST!! Anna must solve this equation.
(x^2)/4=x
Which three steps could Anna use to correctly solve the equation? Select from the drop-down menus to order the steps used to solve the equation.
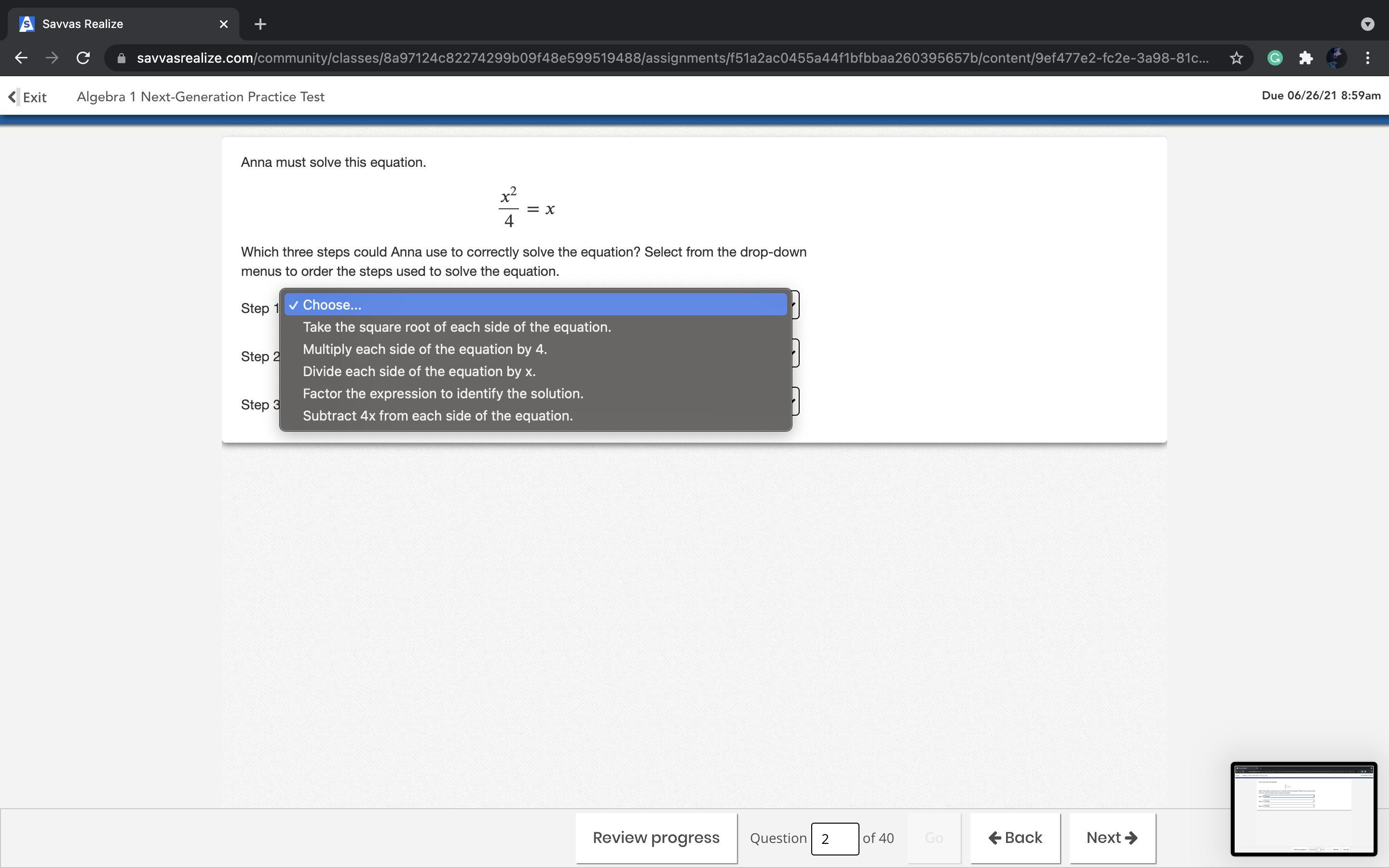


Answers
Answer:
question 1:
step #1:divide both sides by x
step #2:multiply both sides by 4
step #3: plug it into equation
Step-by-step explanation:
question 1:
step #1: divide both sides by x
you get x/4 = 1
step #2:multiply both sides by 4
you get x = 4
step #3: plug it into equation
4 squared/4 = 4
Consider the initial value problem y" + 16 = 48t, y(0) = 5, y'(0) = 2. a. Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y(S). Do not move any terms from one side of the equation to the other (until you get to part (b) below). 48/s^2 help (formulas) b. Solve your equation for Y(s). Y(s) = L{y(t)} = (58^3+2s^2+48)/(s^2(s^2+16)) c. Take the inverse Laplace transform of both sides of the previous equation to solve for y(t).
Answers
a. To solve the initial value problem using Laplace transforms, we start by taking the Laplace transform of both sides of the given differential equation. The Laplace transform of y(t) is denoted as Y(s). The Laplace transform of the second derivative y"(t) can be expressed as s²Y(s) - sy(0) - y'(0), where y(0) and y'(0) are the initial conditions. The Laplace transform of 48t is simply 48/s².
Applying the Laplace transform to the given differential equation, we get:
s²Y(s) - sy(0) - y'(0) + 16Y(s) = 48/s²
Substituting the initial conditions y(0) = 5 and y'(0) = 2, we have:
s²Y(s) - s(5) - 2 + 16Y(s) = 48/s²
Simplifying this equation gives the corresponding algebraic equation in terms of Y(s).
b. Now, we solve the equation obtained in part (a) for Y(s). Rearranging the terms, we have:
(s² + 16)Y(s) = 48/s² + s(5) + 2
Combining like terms, we get:
(s² + 16)Y(s) = (48 + 5s² + 2s) / s²
Dividing both sides by (s² + 16), we obtain:
Y(s) = (48 + 5s² + 2s) / (s²(s² + 16))
So, Y(s) is equal to the Laplace transform of y(t).
c. To find y(t), we take the inverse Laplace transform of Y(s) obtained in part (b). We can use partial fraction decomposition and the properties of Laplace transforms to simplify the expression and find the inverse Laplace transform.
Taking the inverse Laplace transform of Y(s), we find:
y(t) = L^(-1){Y(s)} = L^(-1){(48 + 5s² + 2s) / (s²(s² + 16))}
The inverse Laplace transform can be calculated using tables or software, and it yields the solution y(t) to the initial value problem.
To know more about Laplace transforms, refer here:
https://brainly.com/question/30759963#
#SPJ11
find the difference
5/6-7/10
Answers
Answer:
2/15
Step-by-step explanation:
BRANIEST PLS
Answer: 2/15 is the answer hope this help
Step-by-step explanation:
researchers want to decrease the margin of error by adjusting the confidence level. which confidence interval will have the smallest margin of error (moe)?
Answers
One-sided confidence interval which have the smallest margin of error.
Given that;
Researchers want to decrease the margin of error by adjusting the confidence level.
You cannot be completely certain of the true value of a parameter, such as the mean, if your confidence interval is too broad. However, there are a number of methods you may do to narrow a confidence interval and improve the accuracy of your estimate. The following characteristics have an impact on the confidence interval's width.
one-sided confidence interval:
The margin of error is lower for a one-sided confidence interval than a two-sided confidence interval. A one-sided interval, however, merely shows whether a parameter is larger or less than a cut-off number. A one-sided interval does not reveal anything regarding the parameter's value when viewed from the other direction. Therefore, only use a one-sided confidence interval to boost an estimate's precision when you are concerned that it will either be higher or lower than a cut-off value, but not both.
Hence, we use one-sided confidence interval which have the smallest margin of error.
To learn more about margin of error click here:
brainly.com/question/10501147
#SPJ4
For each of the variables described below, indicate whether it is a quantitative or a categorical (qualitative) variable. Also, indicate the level of measurement for the variable: nominal, ordinal, interval, or ratio. Make sure your responses are the most specific possible.
Variable
Type of variable and Level of measurement
(a) Occupation (Quantitative or Nominal) (Ordinal, Categorical, Interval, Ratio)
(b) Annual salary of a member of the shipping department (Quantitative or Nominal) (Ordinal, Categorical, Interval, Ratio)
(c) Price (in dollars) of a shirt on the clearance rack (Quantitative or Nominal) (Ordinal, Categorical, Interval, Ratio)
Answers
Occupation is a qualitative variable with a nominal level value, annual salary is a quantitative variable with ratio level value, price of a shirt (in dollars) on clearance rack is quantitative with a ratio level value.
Variables can be divided into quantitative or qualitative (categorical).
Quantitative variables are those variables in which the data measures values or counts and is expressed as amounts or numbers. Qualitative variables are any variables whose data are descriptive rather than numerical.
Occupation is a qualitative variable with a nominal level value, because there is no order in the category of occupation, and the variable has no numeric value.Annual salary is a quantitative variable with ratio level value, because annual salary can be measured and takes on numerical values.The price of a shirt (in dollars) on clearance rack is quantitative with a ratio level value, because there is a numerical value (in dollars) that is a quantitative characteristic, it has “true” zero point since zero price in dollars signifies no cost, zero price would have no value at all in any currency.To learn more about quantitative and qualitative, click here:
https://brainly.com/question/14728680
#SPJ4
pleaaeeeeeeee helllppppppp
jack father 4 times old his son five years later both age diffrence is 10 find both age.
Answers
Step-by-step explanation:
Let Jack's present age be x
Hence, his fathers present age=4x
Jacks age after 5 years= (x+5)
Jacks Fathers age after 5 years= (4x+5)
We know.. that the difference between their ages fives years later is 10.. hence
4x+5-(x+5)=10
4x+5-x-5=10
3x = 10
x= 3.3 years old...
Hence,
Jacks present age = 3.3 years
Fathers present age= 13.2 years...
Hope it helps .. I know that the answer comes in decimals... but the questions' like that..
which of the following statements must be true about this diagram? check all that apply. answers are with the picture below:

Answers
The external angle theorem states that the measure of the external angle of a triangle is equal to the sum of the two opposite internal angles.
In this case
\(\angle4=\angle1+\angle2\)Then
∠4 is greater than ∠2 and ∠1, so A and B check
And F also checks
We know that the sum of the internal angles of a triangle add up to 180º so that:
\(\angle1+\angle2+\angle3=180º\)And we also know that ∠3 and ∠4 are a linear pair, this means that they also add up to 180º:
\(\angle3+\angle4=180º\)Since both expressions are equal to 180º we can conclude that they are equal:
\(\angle1+\angle2+\angle3=\angle3+\angle4\)Subtract ∠3 from both sides of the equation and we get that
\(\angle1+\angle2=\angle4\)As stated by the external angle theore, the measure of the external angle, ∠4, of a triangle is equal to the sum of the opposite interior angles, ∠1+∠2 → With this, is proven that F is correct
If angles 1 and 2 add up to angle 4, then, by logic, their measure has to be less than angle 4
→ and this is how you know that ∠1 and ∠2 are less than ∠4
order the following from least to greatest. if there is a tie, indicate that with an equals sign. you do not need to find the values themselves: p′(1), p′(3), p′(6), p′(7), p′(9), p′(10)
Answers
To order the given expressions from least to greatest, we need to find the values of each expression. However, since we do not have the function p(x), we cannot find the values of p′(1), p′(3), p′(6), p′(7), p′(9), and p′(10). Therefore, we cannot order the expressions from least to greatest.
It is important to note that the sign of each expression will depend on the function p(x) and its derivative p′(x). If p′(x) is positive, then the function p(x) is increasing at that point. If p′(x) is negative, then the function p(x) is decreasing at that point. Without the function p(x), we cannot determine the sign of each expression and therefore cannot order them from least to greatest.
In conclusion, without the function p(x), we cannot order the expressions p′(1), p′(3), p′(6), p′(7), p′(9), and p′(10) from least to greatest.
Learn more about expressions
brainly.com/question/14083225
#SPJ11
A store has sold 90 notebooks, which is 20% of all the notebooks they had. How many notebooks did the store have at first?
Answers
Answer:
450
Step-by-step explanation: