1489.45 Round this number to two decimal places
Answers
i dont know sd f g d g g
Related Questions
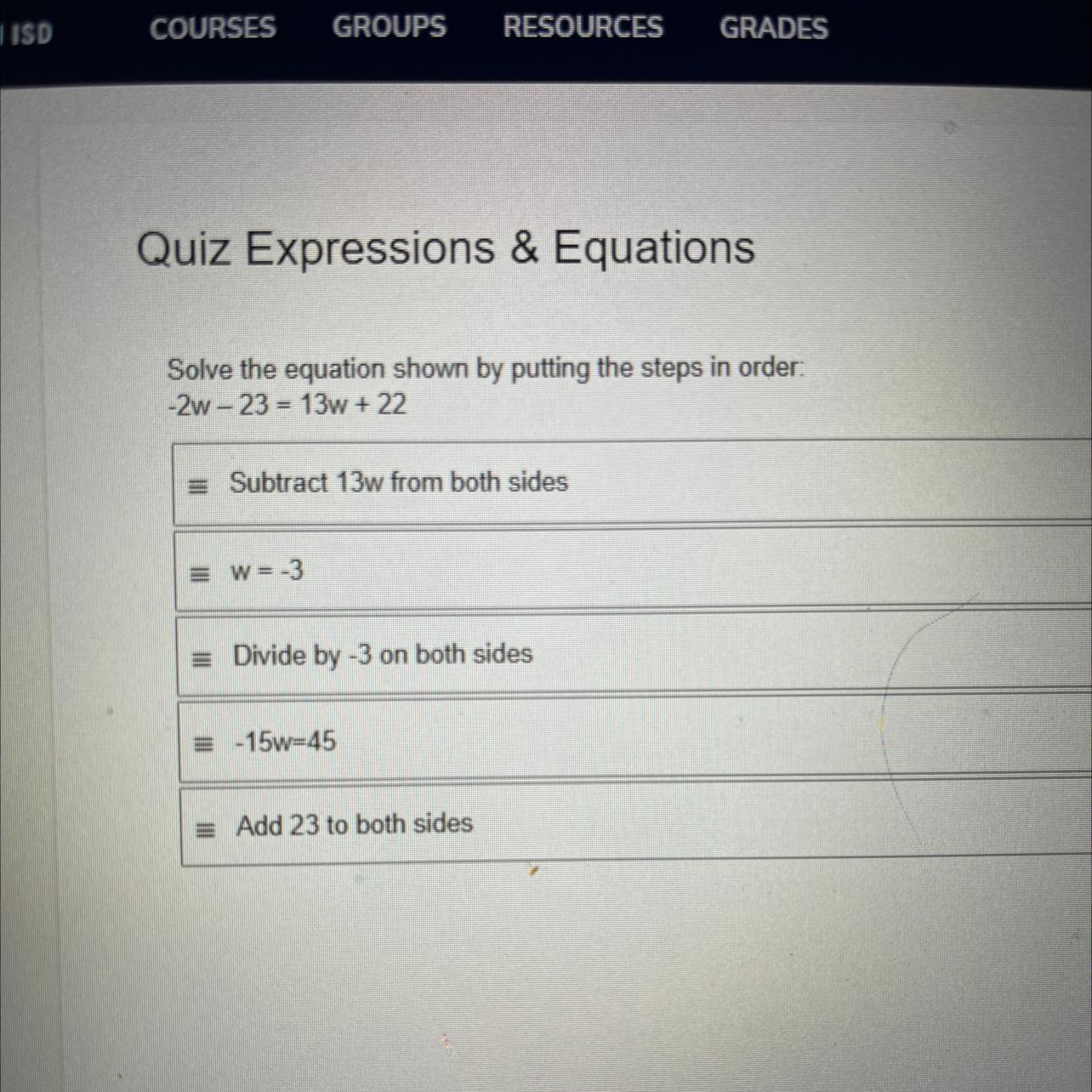
Solve the equation shown by putting the steps in order:
-2w-23 = 13w + 22
= Subtract 13w from both sides
= w=-3
= Divide by -3 on both sides
= -15w=45
= Add 23 to both sides
Answers
Subtract 13w
-15w=44
Divide
w=-3
Find the measure of the three missing angles in the parallelogram below
128⁰

Answers
Answer: x = 52, y = 128, z = 52
Step-by-step explanation:
Line t is tangent to the circle. Find m/1
D₂0
260°
1
m/1 =

Answers
Based on the Inscribed Angle Theorem, the measure of angle 1 is calculated as: m<1 = 130°.
What is the Inscribed Angle Theorem?The Inscribed Angle Theorem states that an angle inscribed in a circle is half the measure of the central angle that intercepts the same arc and also half of the intercepted arc measure itself.
In other words, if we draw a circle and a chord inside the circle, and then draw an angle with its vertex on the circle and its rays intersecting the chord and the circle, then the measure of this angle is half the measure of the central angle that has the same endpoints on the circle as the inscribed angle and intercepts the same arc.
Applying this theorem, we have:
measure of angle 1 = 1/2 * (260°)
measure of angle 1 = 260/2
Measure of <1 = 130°
Learn more about Inscribed Angle Theorem on:
https://brainly.com/question/3538263
#SPJ1
what is relative intrest
Answers
Relative interest refers to the comparison of interest rates between different financial instruments or investment opportunities. It allows individuals or investors to assess and evaluate the attractiveness of various options based on their potential returns.
1. Understand the basic concept: Interest is the cost of borrowing money or the return earned on invested funds. Relative interest involves comparing the interest rates of different financial instruments or investments to determine which one offers a more favorable return.
2. Identify the investment options: Start by identifying the different investment opportunities or financial instruments available. These can include savings accounts, certificates of deposit (CDs), bonds, stocks, or other investment vehicles.
3. Research interest rates: Research and gather information about the current interest rates offered by each investment option. This information can usually be found on financial websites, through financial institutions, or by consulting with a financial advisor.
4. Compare interest rates: Once you have the interest rates for each investment option, compare them side by side. Look for the differences in rates and identify which options offer higher or lower returns.
5. Assess risk and return: Consider the level of risk associated with each investment option. Higher returns often come with higher risk, so it's essential to evaluate the risk-reward tradeoff.
6. Make an informed decision: Based on the comparison of interest rates and the risk-reward assessment, make an informed decision on which investment option aligns with your financial goals and risk tolerance.
Always remember to consider your financial goals, risk tolerance, and consult with a financial advisor if needed.
For more such questions on interest rates, click on:
https://brainly.com/question/25720319
#SPJ8
a slow pitch softball diamond is 65-foot square with a base at each corner. if catcher throws directly from home plate to second how many feet will ball travel?

Answers
Given that,
slow pitch softball diamond is 65-foot square with a base at each corner
if catcher throws directly from home plate to second , to find the number of feet will ball travel
That is to find the diagonal of the shape (square), by pythagoras theorem, we get,
Square of the hypotenuse is equal to the square of the sum of the other two sides.
we get,
Distance the ball travel is
\(\sqrt[]{65^2+65^2}\)\(=65\sqrt[]{1+1}\)\(=65\sqrt[]{2}\)Answer is: 65 root 2 ft.
What is 255 x 270 + 460

Answers
Answer:
69310
Step-by-step explanation:
255*270+460
=68850+460
=69310
A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by h(t)= −4.9t^2+11t+7. How many seconds does it take to reach maximum height? Enter the answer with at least 3 decimal places.
Answers
Given statement solution is :- It takes approximately 1.122 seconds for the ball to reach its maximum height.
To find the time it takes for the ball to reach its maximum height, we need to determine the vertex of the parabolic function given by the equation h(t) = \(-4.9t^2 + 11t + 7.\)
The vertex of a parabola in the form y = \(ax^2 + bx\) + c is given by the formula t = -b / (2a).
Comparing the equation h(t) = \(-4.9t^2 + 11t + 7\) to the standard form, we have:
a = -4.9
b = 11
Using the formula for the vertex, we can calculate the time it takes to reach the maximum height:
t = -11 / (2 * -4.9)
t = -11 / -9.8
t ≈ 1.122
Therefore, it takes approximately 1.122 seconds for the ball to reach its maximum height.
For such more questions on Max height
https://brainly.com/question/12446886
#SPJ8
Help!!!! Please
Asap

Answers
Answer:
events at A and B are independent because P(A)(B)≠P(A)
Find the distance traveled in 25 seconds by an object traveling at a velocity of v(t) = 20 + 5cos(t) feet per second
Answers
Answer:
499.338 feet
Step-by-step explanation:
You want to know the distance traveled by an object in 25 seconds when its velocity is described by 20+5cos(t) feet per second.
DistanceThe distance an object travels is the integral of its velocity. For the given velocity and time period, the distance is ...
\(\displaystyle d=\int_0^{25}{v(t)}\,dt=\int_0^{25}{(20+5\cos(t))}\,dt=(20t+5\sin(t))|_0^{25}\\\\d=500+5\sin(25)\approx\boxed{499.338\quad\text{feet}}\)

The distance traveled in 25 seconds is 499.33 feet.
It is required to find the distance traveled in 25 seconds.
What is distance?The distance of an object can be defined as the complete path travelled by an object .Distance is a scalar quantity that refers to "how much ground an object has covered" during its motion.
Given:
We have to find the distance , we will integrate v(t) from 0 to 25 second.
Consider an object traveling at constant velocity v = k. Then, each second, it travels k feet, so after t seconds, the distance traveled is k*t.
Now, suppose its speed increases by 1 feet/sec . So, estimate for distance traveled after t seconds is
1 + 2 + 3 + 4 + ... + t = t(t+1)/2, or approximately 1/2 t^2.
According to given question we have
Given a velocity function v, the distance s is figured by taking the integral. In this case,
v = 20 + 5 cos(t)
s = 20t + 5 sin(t) from 0 to 25
= s(45)-s(0)
s(0) = 0
so, the distance is
s(25) = 20*25 + 5sin(25)
= 500 -0.661
=499.33 feet.
Therefore, the distance traveled in 25 seconds is 499.33 feet.
Learn more about distance here:
brainly.com/question/28304899
#SPJ1
The rental rate for a power washer has a one time fee of $60 plus $20 for each day of the rental. The graph shows the points representing the total cost of the rental. 150 (4,140) 125 Total Cost 100 (2,100) 75 50 25 1 2 3 Days Write an equation, in slope-intercept formly = mx + b) that models the total cost of the rental over time.
Answers
I think it’s
Y=25x+50
Hope this helps
which one of the following is a solution to |2x-1|>3 A.2, B.-1, C.-2, D.1, E.None of these
Answers
Therefore x>2 or x<-2
—> E
The volume of a cube that is 2.9 x 5 x 4
Answers
The volume of the cuboid is 58 cubic units.
What is a cuboid?A cuboid is a 3 dimensional figure that has six rectangular faces. So that the volume of a cuboid can be determined by;
volume of cuboid = length x width x height
From the given question, we have;
the volume of a cuboid that is 2.9 x 5 x 4 can be determined as follows;
volume of cuboid = length x width x height
= 2.9 x 5 x 4
= 58
The volume of the cuboid with the given dimension is 58 cubic units.
Learn more about volume of a cuboid at https://brainly.com/question/46030
#SPJ1
Which integer is 6√ closest to?
Answers
Answer:
2
Step-by-step explanation:
you would first take the square root of 6 and get 2.449...
then you would round it to the nearest whole number and get 2
Answer:
2
Step-by-step explanation:
if sqrt(4) = 2 and sqrt(9) =3, then sqrt(6) is between 2 and 3, but closer to 2.
I need to know how to simplify 18 - 9 x (-4) ÷ 3 + 10 x 2
Answers
Okay let’s put PEMDAS into mind.
PEMDAS: parenthesis, exponents, multiplication, division, addition, subtraction (left to right)
18-9•(-4) /3 +10•2
Multiplication & Division comes first (left to right) so...
-9•(-4) = 36
bring down the divided by 3...
36/3 = 12
Bring the whole equation down...
18+12+10•2
Once again, there is another to multiply so...
10•2 = 20
18+12+20
All is the same so add them up to get...
50
^ That’s the answer.
18-9(-4)/3+10•2
18-(-36)/3+20
18-(-12)+20
18-8
10
A model village is built to scale. It has a scale of 1 : 23. A road has a real-life length of 1.61 km. What is the length of the road in the model village in m?
Answers
Answer:
We need to find how much more or less the ratio becomes
1.61 / 23 = 0.07
we multiply 0.07 with 1 to make the ratio even and get your answer
1 x 0.07 = 0.07 on the map
Hope this helps
Step-by-step explanation:
What is the equation for the line in the slope-intercept form enter your answer in the box
Answers
Answer:
y=mx+b I believe is what your looking for
Simplify.
14.8 + 6.25 + 0.97
Answers
Answer:
22.02
Step-by-step explanation:
pleaseeee someone help me with this asap

Answers
The required maximum value is 6
And Y intercept is 5.
The given function is
f(x) = √(x+9) + 2
Now to find the maxima and minima at the given interval,
The appropriate method is to plot the graph of the given function,
Now put values of x from the interval [-9, 7] and get the corresponding values of function and mark them on the graph paper.
Now after plotting figure we get
In the given interval [-9, 7]
The function attains maximum value at 7 = 6
And the Y intercept of function is at 5
To learn more about function visit:
https://brainly.com/question/8892191
#SPJ1

(6x + 1) + (-8x – 2) HELP FAST!!!

Answers
Answer:
-2x-4 is the answer
Step-by-step explanation:
................
544 is what percent of 640?
Answers
Answer:
\( = \frac{544}{640} \times 100\%\)
\( = 85\%\)
The recursive formula, an = an-1 - 12 with a0 = 84 describes the amount of water left, in gallons, in a bathtub n after the drain stopper was pulled. Find a5, he amount of water left in the tub after 5 minutes.
Answers
================================================
Work Shown:
\(a_n = a_{n-1} - 12\\\\a_1 = a_{1-1} - 12\\\\a_1 = a_{0} - 12\\\\a_1 = 84 - 12\\\\a_1 = 72\\\\\)
After 1 minute, there are 72 gallons of water left.
\(a_n = a_{n-1} - 12\\\\a_2 = a_{2-1} - 12\\\\a_2 = a_{1} - 12\\\\a_2 = 72 - 12\\\\a_2 = 60\\\\\)
After 2 minutes, there are 60 gallons left.
\(a_n = a_{n-1} - 12\\\\a_3 = a_{3-1} - 12\\\\a_3 = a_{2} - 12\\\\a_3 = 60 - 12\\\\a_3 = 48\\\\\)
After 3 minutes, there are 48 gallons left.
\(a_n = a_{n-1} - 12\\\\a_4 = a_{4-1} - 12\\\\a_4 = a_{3} - 12\\\\a_4 = 48 - 12\\\\a_4 = 36\\\\\)
After 4 minutes, there are 36 gallons left.
\(a_n = a_{n-1} - 12\\\\a_5 = a_{5-1} - 12\\\\a_5 = a_{4} - 12\\\\a_5 = 36 - 12\\\\a_5 = \boldsymbol{24}\\\\\)
After 5 minutes, there are 24 gallons left.
------------------------
Table of values
\(\begin{array}{|c|c|} \cline{1-2}n & a_n\\\cline{1-2}0 & 84\\\cline{1-2}1 & 72\\\cline{1-2}2 & 60\\\cline{1-2}3 & 48\\\cline{1-2}4 & 36\\\cline{1-2}5 & \boldsymbol{24}\\\cline{1-2}\end{array}\)
Mis directly proportional to r?
When r= 2, M= 14
a) Work out the value of M when r= 12.
b) Work out the value of r when M = 224.
Answers
Answer:
M = 84 , r = 32
Step-by-step explanation:
Given M is directly proportional to r then the equation relating them is
M = kr ← k is the constant of proportion
To find k use the condition when r = 2, M = 14 , then
14 = 2k ( divide both sides by 2 )
7 = k
M = 7r ← equation of proportion
(a)
When r = 12
M = 7 × 12 = 84
(b)
When M = 224 , then
224 = 7r ( divide both sides by 7 )
32 = r
According to an NRF survey conducted by BIGresearch, the average family spends about $237 on electronics (computers, cell phones, etc.) in back-to-college spending per student. Suppose back-to-college family spending on electronics is normally distributed with a standard deviation of $54. If a family of a returning college student is randomly selected, what is the probability that: (a) They spend less than $150 on back-to-college electronics? (b) They spend more than $390 on back-to-college electronics? (c) They spend between $120 and $175 on back-to-college electronics?
Answers
Answer:
(a) Probability that a family of a returning college student spend less than $150 on back-to-college electronics is 0.0537.
(b) Probability that a family of a returning college student spend more than $390 on back-to-college electronics is 0.0023.
(c) Probability that a family of a returning college student spend between $120 and $175 on back-to-college electronics is 0.1101.
Step-by-step explanation:
We are given that according to an NRF survey conducted by BIG research, the average family spends about $237 on electronics in back-to-college spending per student.
Suppose back-to-college family spending on electronics is normally distributed with a standard deviation of $54.
Let X = back-to-college family spending on electronics
SO, X ~ Normal(\(\mu=237,\sigma^{2} =54^{2}\))
The z score probability distribution for normal distribution is given by;
Z = \(\frac{X-\mu}{\sigma}\) ~ N(0,1)
where, \(\mu\) = population mean family spending = $237
\(\sigma\) = standard deviation = $54
(a) Probability that a family of a returning college student spend less than $150 on back-to-college electronics is = P(X < $150)
P(X < $150) = P( \(\frac{X-\mu}{\sigma}\) < \(\frac{150-237}{54}\) ) = P(Z < -1.61) = 1 - P(Z \(\leq\) 1.61)
= 1 - 0.9463 = 0.0537
The above probability is calculated by looking at the value of x = 1.61 in the z table which has an area of 0.9463.
(b) Probability that a family of a returning college student spend more than $390 on back-to-college electronics is = P(X > $390)
P(X > $390) = P( \(\frac{X-\mu}{\sigma}\) > \(\frac{390-237}{54}\) ) = P(Z > 2.83) = 1 - P(Z \(\leq\) 2.83)
= 1 - 0.9977 = 0.0023
The above probability is calculated by looking at the value of x = 2.83 in the z table which has an area of 0.9977.
(c) Probability that a family of a returning college student spend between $120 and $175 on back-to-college electronics is given by = P($120 < X < $175)
P($120 < X < $175) = P(X < $175) - P(X \(\leq\) $120)
P(X < $175) = P( \(\frac{X-\mu}{\sigma}\) < \(\frac{175-237}{54}\) ) = P(Z < -1.15) = 1 - P(Z \(\leq\) 1.15)
= 1 - 0.8749 = 0.1251
P(X < $120) = P( \(\frac{X-\mu}{\sigma}\) < \(\frac{120-237}{54}\) ) = P(Z < -2.17) = 1 - P(Z \(\leq\) 2.17)
= 1 - 0.9850 = 0.015
The above probability is calculated by looking at the value of x = 1.15 and x = 2.17 in the z table which has an area of 0.8749 and 0.9850 respectively.
Therefore, P($120 < X < $175) = 0.1251 - 0.015 = 0.1101
PLEASE HURRY 100P I REALLY NEED THIS!!!!!

Answers
The range of the data is 30, and the interquartile range (IQR) is 15.
To create a box plot using the given data, we first need to determine the five-number summary, which includes the minimum value, the first quartile (Q1), the median (Q2), the third quartile (Q3), and the maximum value.
From the given data, we can determine the five-number summary as follows:
Minimum: 60
Q1: 70
Median (Q2): 80
Q3: 85
Maximum: 90
Now, let's create a box plot using this information:
```
| | | | |
60 |––––––––|––––––––| |
| | | | |
70 |––––––––|––––––––|––––––––|––––––––|
| | | | |
80 |––––––––|––––––––|––––––––|––––––––|
| | | | |
90 |––––––––|––––––––| |
| | | | |
------------------------------------
60 70 80 90
```
In the box plot, the line within the box represents the median (Q2), the box represents the interquartile range (IQR) from Q1 to Q3, and the lines extending from the box (whiskers) represent the minimum and maximum values. Any data points falling outside the whiskers would be considered outliers.
The range can be calculated as the difference between the maximum and minimum values:
Range = Maximum - Minimum = 90 - 60 = 30
The interquartile range (IQR) is the difference between the third quartile (Q3) and the first quartile (Q1):
IQR = Q3 - Q1 = 85 - 70 = 15
Therefore, the range of the data is 30, and the interquartile range (IQR) is 15.
for more such question on range visit
https://brainly.com/question/30389189
#SPJ8
what is the solution to the equation below? sqrt 2-3x / sqrt 4x =2
Answers
The solution to the equation sqrt 2-3x / sqrt 4x = 2 is x = -2/3.
To solve the equation, we must first clear the denominators and simplify the equation. We can do this by multiplying both sides by sqrt(4x) and then squaring both sides. This gives us:
sqrt 2-3x = 4sqrt x
2 - 6x + 9x² = 16x
9x² - 22x + 2 = 0
Using the quadratic formula, we can find that x = (-b ± sqrt(b² - 4ac)) / 2a. Plugging in a = 9, b = -22, and c = 2, we get:
x = (-(-22) ± sqrt((-22)² - 4(9)(2))) / 2(9)
x = (22 ± sqrt(352)) / 18
x = (22 ± 4sqrt22) / 18
Simplifying this expression, we get:
x = (11 ± 2sqrt22) / 9
Therefore, the solution to the equation is x = -2/3.
To solve the equation sqrt 2-3x / sqrt 4x = 2, we must clear the denominators and simplify the equation. This involves multiplying both sides by sqrt(4x) and then squaring both sides.
After simplifying, we end up with a quadratic equation. Using the quadratic formula, we can find that the solutions are x = (11 ± 2sqrt22) / 9.
However, we must check that these solutions do not result in a division by zero, as the original equation involves square roots. It turns out that the only valid solution is x = -2/3.
Therefore, this is the solution to the equation.
for such more questions on solution
https://brainly.com/question/24644930
#SPJ8
Find the distance between the two points rounding to the nearest tenth (if necessary).
(-4,2) and (2,-6)
Answers
Answer:
10
Step-by-step explanation:
Distance formula:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Let \((x_1,y_1)\) = (-4, 2)
Let \((x_2,y_2)\) = (2, -6)
Substituting given points into the formula:
\(\implies d=\sqrt{(2-(-4))^2+(-6-2)^2}\)
\(\implies d=\sqrt{(6)^2+(-8)^2}\)
\(\implies d=\sqrt{36+64}\)
\(\implies d=\sqrt{100}\)
\(\implies d=10\)
Graph XY with endpoints X(-3, 1) and Y(4,-5) and its image after the composition.
Translation: (x, y)→(x, y + 2)
Rotation: 90° about the origin
Answers
The graph of its image after the composition is shown in graph.
We have to given that;
XY with endpoints are,
⇒ X (-3, 1) and Y (4,-5)
Now, After Translation (x, y)→(x, y + 2) we get;
X = (- 3, 1)
X' = (- 3, 1 + 2) = (- 3, 3)
Y = (4, - 5)
Y' = (4, - 3)
And, After Rotation: 90° about the origin.
That is, (x, y) = (y, - x)
The points of image are,
X'' = (3, 3)
Y'' = (- 3, - 4)
Thus, The graph of its image after the composition is shown in graph.
Learn more about the transformation visit:
https://brainly.com/question/30097107
#SPJ1

Which graph represents the System of inequalities shown below? y < -2x + 2
y > x - 1

Answers
Answer:
The second one (Top right)
What type of angle are angles 1 and 14

Answers
Answer:
1 is 45. 14 is 90
Step-by-step explanation:
The competitive advantage of small American factories such as Tolerance Contract Manufacturing lies in their ability to produce parts with highly narrow requirements, or tolerances, that are typical in the aerospace industry. Consider a product with specifications that call for a maximum variance in the lengths of the parts of 0.0008. Suppose the sample variance for 30 parts turns out to be s2 = 0.0009.
Required:
Use α = 0.05 to test whether the population variance specification is being violated. State the null and alternative hypotheses.
Answers
Answer:
Following are the solution to the given question:
Step-by-step explanation:
Please find the complete question in the attached file.
\(H_0: \sigma^{2} \leq 0.0008\\\\H_a: \sigma^{2} > 0.0008\)
The testing states value is:
\(\to x^2=\frac{(n-1)s^2}{\sigma^2}=32.6250\)
therefor the \(\rho - \ value = 0.2931\)
Through out the above equation its values Doesn't rejects the H_0 value, and its sample value doesn't support the claim that although the configuration of its dependent variable has been infringed.
