you guys are worth it!
Answers
Answer:
i know im amazing
Step-by-step explanation:
Answer:
Awwwww thank you!!! Your worth more than the stars above. THANKS FOR THE POINTS!!!!
Step-by-step explanation:
P.S. I love your pfp!!!!
Related Questions
I WILL GIVE YOU BRAINLIEST,5 STARS, AND THANKS.(P.S. AT LEAST TWO PEOPLE GIVE ANSWER SO I CAN GIVE BRAINLIEST)

Answers
Answer:
A
Step-by-step explanation:
the other options have a common difference
Answer:
A is not arithmetic series
Step-by-step explanation:
In B,C and D there is arithmetic series as a2-a1=a3-a2
In A. there is no such series.....
Jeff wants to build a barn that is 50 ] feet long by 204 feet wide. What is the area of the barn in square feet?
Answers
Answer:
10200\
\\\\SHREKS GAYSDEWD
Step-by-step explanation:
the answer is 10200
Shelia walks 2.75 km every Monday. If
she does this for 8 weeks in a row, how
many km will she have walked?
Answers
Answer:
22km
Step-by-step explanation:
As Sheila only walks 2.75 km one day out of the week, then she walks 2.75km/week. Because of this, the answer can be found by multiplying 2.75 by 8.
Writing The graph shows a proportional relationship between the variables y and x. Write an equation to model
the relationship. Use pencil and paper. Explain how you know there is a proportional relationship if you are given
either an equation or a graph.
the equation y= (blank) models the relationship.
the graph picture is the one that will help you figure it out

Answers
Answer:
y x
..........
....................
PLEASE HELP MEEEEEE!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
34
Step-by-step explanation:
every corner here is 90⁰,because it says so.
QRP would be 90-56 =34⁰ and the opposite corner is the same,so 34⁰
Answer:
34
Step-by-step explanation:
KRL = QRP, so finding QRP can get us our answer. We were given 56 and 90 because 90 is the degree of a right angle.
A straight line is 180 degrees.
If we subtract 90 and 56 from that 180, we'll find out QRP
180-90=90
90-56=34
Since QRP = 34, that means KRL does also
differences on the dependent measure between the levels of one variable within one level of another variable are known as
Answers
The differences in dependent measures between levels are the main effects
The differences in the dependent measure between the levels of one variable within one level of another variable are known as simple main effects. These effects can be tested statistically to determine if they are statistically significant, which would indicate that the difference between the levels of the first variable is meaningful within the context of the second variable.
One independent variable having a certain degree of another independent variable is the simple main effect of a factorial experiment. The levels of the other independent variable are averaged over the primary effect of one independent variable. Results for a straightforward main effect are examined as though every level of the other independent variables had its own experiment.
Read more about the main effects on:
https://brainly.com/question/29613380
#SPJ4
Line x is parallel to line y. Line z intersect lines x and y. Determine whether each statement is Always True.

Answers
Line x is perpendicular to line y. Line z crosses lines x and y. Only statements 3 and 4 are true.
∠6 = ∠8 is not true because they both lie on the same plane and makes an angle of 180° and can never be true. ∠6 = ∠1 is also not true because ∠1 is clearly obtuse angle and ∠6 is clearly acute angle so they cannot be equal. Hence, statement a and b are false.
∠7 = ∠3 is always true because they are corresponding angles and corresponding angles are always equal. m∠2 + m∠4 = 180° is also true because they lie on same plane and have common vertex and hence, they are supplementary angles and make a sum of 180°. Hence, statement 3 and 4 is always true.
To know more about corresponding angles:
https://brainly.com/question/12521848
#SPJ1
For what values of x and y are the triangles to the right congruent by HL

Answers
Answer:
x = 2 , y = 1
Step-by-step explanation:
For the triangles to be congruent then the hypotenuse and leg must be congruent, that is
x = y + 1 → (1)
4y = x + 2 → (2)
Substitute x = y + 1 into (2)
4y = y + 1 + 2
4y = y + 3 ( subtract y from both sides )
3y = 3 ( divide both sides by 3 )
y = 1
Substitute y = 1 into (1)
x = y + 1 = 1 + 1 = 2
6 1/4 - 2 3/8 explain
Answers
it is 3.875
if you subract the two fraction it makes 31/8. then devide it which makes 3.875
Explanation: 31/8 or 3 7/8
6 1/4 = 25/4
2 3/8 = 19/8
25/4 - 19/8
= 50/8 - 19/8
= 31/8
Which of the following conditions must be met in order to construct a 99% confidence interval for the true mean difference in pretest and posttest scores? (a) The distribution of both pretest scores and posttest scores must be approximately Normal. (b) The distribution of pretest scores and the distribution of differences (post-pre) must be approximately Normal (c) Only the distribution of pretest scores must be approximately Normal (d) Only the distribution of differences (post --pre) must be approximately Normal. (c) All three distributions (pretest, postecst, and the difference) must be approximately Normal.
Answers
The correct answer is (c) Only the distribution of pretest scores must be approximately Normal
How is conditions for 99% CI calculation?
In order to construct a 99% confidence interval for the true mean difference in pretest and posttest scores, we need to meet certain conditions. The only condition that must be met is that the distribution of pretest scores should be approximately Normal. This means that the data collected from the pretest should follow a bell-shaped curve, with the majority of the scores being clustered around the mean. This condition is important because it helps us to make accurate statistical inferences about the population mean difference based on the sample data. The distribution of posttest scores or the difference between posttest and pretest scores are not required to be normal for constructing a confidence interval.
Learn more about 99% confidence
brainly.com/question/30762304
#SPJ11
To construct a 99% confidence interval for the true mean difference in pretest and posttest scores, the condition that must be met is only the distribution of differences (post-pre) must be approximately Normal. Thus, the correct option is D.
When constructing a confidence interval for the true mean difference in pretest and posttest scores, it is only necessary for the distribution of the differences to be approximately Normal. The distributions of the pretest and posttest scores themselves do not need to be Normal, as long as the difference between them is approximately Normal.
However, if all three distributions (pretest, posttest, and the difference) are approximately Normal, this can improve the accuracy and precision of the confidence interval.
Therefore, D is the correct option.
To know more about Pretest - Posttest visit:
https://brainly.com/question/31803047
#SPJ11
There are six Mountain Dews, four Pepsis, five Sierra Mists, nine Orange Crushes, seven NuGrapes, three Mug root beers, and six Canada Dry ginger ales in the fridge. Find the probability of selecting a NuGrape or a ginger ale. Show work
Answers
I Hope it is correct
Step-by-step explanation:
The total number of sodas in the fridge is:
6 + 4 + 5 + 9 + 7 + 3 + 6 = 40
The number of NuGrapes or ginger ales is:
7 (NuGrapes) + 6 (Canada Dry ginger ales) = 13
The probability of selecting a NuGrape or a ginger ale is the number of favorable outcomes (selecting a NuGrape or a ginger ale) divided by the total number of possible outcomes (selecting any soda):
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 13 / 40
Probability = 0.325
So, the probability of selecting a NuGrape or a ginger ale is 0.325 or 32.5%.
Evaluate: 3(2f - g) + 4h for f = 2, g = -1 and h = 3
Answers
Answer:
27
Step-by-step explanation:
6f - 3g + 4h
6(2) - 3(-1) + 4(3)
12 + 3 + 12
27
Answer:
Step-by-step explanation:
3(2(2) + 1 ) + 4(3)
3(4 + 1) + 12
3(5) + 12
15 + 12
27
In Lily's garden, there are 5 rose bushes the first year. Each year, she adds two new rose bushes. She
has 20 tulip plants the first year and loses 3 each year. When will the number of rose bushes equal
the number of tulip plants? Use graphing to find the solution.
Answers
Step-by-step explanation:
Let x = the number of years since the first year and let y = the total number of plants.
Roses: y = 5 + 2x
Tulips: y = 20 – 3x
You can use elimination to solve.
y = 5 + 2x
(-)y = 20 – 3x
0 = -15 + 5x
15 = 5x
3 = x
This means that 3 years after the first year, the number of rose bushes equals the number of tulip plants.
The graphs appear to
intersect at (3, 11) which verifies that x=3

The number of rose bushes will equal the number of tulip plants after 3 years
How to determine the year?The given parameters are:
Rose bushes
Initial = 5Additional = 2Tulip bushes
Initial = 20Additional = -3So, the number of rose bushes and tulip bushes each year is:
y = 5 + 2x
y = 20 - 3x
From the graph of both equations, we have:
(x,y) = (3,11)
Hence, the number of rose bushes will equal the number of tulip plants after 3 years
Read more about linear equations at:
https://brainly.com/question/14323743

((-5) - 9+ (7+(-6)))*(-4)
Answers
Answer:
The answer to ((-5) - 9+ (7+(-6)))*(-4) is 52
\(\sf Answer: \)
\(52\)
\(\sf Step-By-Step~ Explanation: \)
\(Equation\)
\(((-5) - 9 + (7+(-6))) \times (-4)\)
\(Subtract~~9~~and~~-5 = -14.\)
\((-14 + 7 - 6)~(-4)\)
\(Add~~-14~~and~~7 = -7\)
\((-7-6)~(-4)\)
\(Subtract~~6~~and~~-7 = -13\)
\(-13~(-4)\)
\(Lastly,~~multiply~~-13~~and~~-4 = 52\)
\(52\)
\(\huge\boxed{\sf Answer \ 52}\)
2b +4= -8
29 - 6 = 4
3s – 4= 8
can some one pls help me with these 3 question pls
Answers
Answer: 2b+4=-8 the answer is -6
Step-by-step explanation: I got this because you subtract 4 from both side which subtract 4 from 4 and subtract -8 from -4 you add those two up because they are both negative which you got -12 so your equation right now is 2b=-12 after that you divide 2 from 2b from both side and your answer is -6. I hope I helped with that one problem
How do I do this problem? We’ve been learning this recently and there’s a test we have on Thursday And I’m still not quite sure how to do these types of problems

Answers
Answer:
I have a test on thursday toooooooo
Step-by-step explanation:
{y=10x+2
-5x+4y=-27
this is systems of equations
Answers
\(y = 10x +2~~....(i) \\\\-5x +4y = -27~~....(ii)\\\\\text{Substitute y =10x+2 in equation (ii):}\\\\\\-5x +4(10x+2) = -27 \\\\\implies -5x + 40x + 8 +27 =0\\\\\implies 35x +35=0\\\\\implies 35(x +1) =0\\\\\implies x +1 = 0 \implies x = -1\\\\\text{Substitute} ~x =-1 ~ \text{in equation (i):}\\\\y = 10(-1) +2 = -10+2 = -8 \\\\\\\text{Hence}~ (x,y) = (-1,-8)\)
Answer:
(x, y) = (19/35, 52/7)
Step-by-step explanation:
When you have an expression for one of the variables, the "substitution" method of solution is a reasonable choice. Here, we have an expression for y that can be substituted into the second equation.
-5x +4(10x +2) = 27
35x +8 = 27 . . . . . . . simplify
35x = 19 . . . . . . . subtract 8
x = 19/35 . . . . divide by the coefficient of x
y = 10(19/35) +2 = 52/7
The solution is (x, y) = (19/35, 52/7).
I need help finding the answer
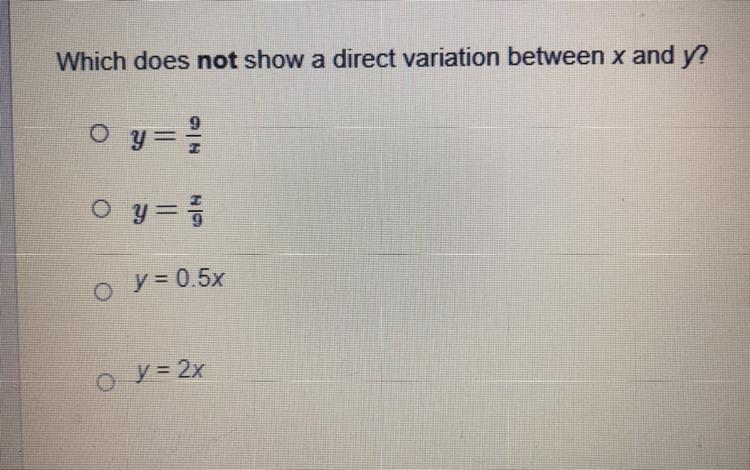
Answers
I guess option A is the correct answer
a30 arithmetic sequence of 1,-4,-9,-14
Answers
The 30th term a30 of the sequence is -1445
How to determine the value of a30?The definition of the function is given as
arithmetic sequence of 1,-4,-9,-14
The above definitions imply that we simply subtract 5 from the previous term to get the current term
Using the above as a guide,
so, we have the following representation
First term, a = 1
Common difference, d = 5
An arithmetic sequence is represented as
a(n) = a + (n - 1)d
For the 30th term, we have
a(30) = a + 29d
So, we have
a(30) = 1 + 29 * -5
Evaluate
a(30) = -144
Hence, the value of a30 is -144
Read more about sequence at
brainly.com/question/7882626
#SPJ1
31. solve the initial value problem y′ = 2y2 xy2 , y(0) = 1 and determine where the solution attains its minimum value.
Answers
The solution attains its minimum value of -2/3 at x = -1.
To solve the initial value problem y′ = 2y^2 + xy^2, y(0) = 1, we can use the method of separation of variables.
First, we rewrite the equation as:
y′ = y^2(2 + x)
Then, we separate the variables and integrate both sides:
1/y^2 dy = (2 + x) dx
Integrating both sides, we get:
-1/y = x + x^2/2 + C
where C is the constant of integration. To find C, we use the initial condition y(0) = 1, which gives:
-1/1 = 0 + 0 + C
C = -1
Substituting C back into the equation, we get:
-1/y = x + x^2/2 - 1
Solving for y, we get:
y(x) = -1/(x + x^2/2 - 1)
To find the minimum value of y, we can take the derivative of y(x) and set it equal to zero:
y'(x) = 1/((x + x^2/2 - 1)^2)(1 + x) = 0
Solving for x, we get:
x = -1
Substituting x = -1 back into the expression for y(x), we get:
y(-1) = -1/(-1 + (-1)^2/2 - 1) = -2/3
Learn more about initial value problem here
brainly.com/question/30547172
#SPJ4
The given question is incomplete, the complete question is:
Solve the initial value problem y′ = 2y^2 + xy^2 , y(0) = 1 and determine where the solution attains its minimum value.
Can you help me solve 4x5/7.
Answers
Answer:
2.85 have a nice day
Step-by-step explanation:
4x5=20 then you dived 20 by 7 and you get 2.85
Using simplex method to solve the following problems: (Manual calculations and then confirm your calculation by any software) Max. Z=5A+4B Subject to constraints: 6 A+4 B≤24, A+2 B≤6,−A+B≤1, B≤2, A, B≥0
Answers
Using the simplex method, the maximum value of Z=5A+4B is found to be 19.2 when A=3.6 and B=1.2. The calculations can be confirmed by using any software that solves linear programming problems.
To solve the given linear programming problem using the simplex method, we start by converting the problem into standard form. We introduce slack variables to convert the inequalities into equations.The initial tableau is as follows:
| A | B | S1 | S2 | S3 | S4 | RHS
------------------------------------------
Z | -5 | -4 | 0 | 0 | 0 | 0 | 0
------------------------------------------
S1 | 6 | 4 | 1 | 0 | 0 | 0 | 24
S2 | 1 | 2 | 0 | 1 | 0 | 0 | 6
S3 | -1 | 1 | 0 | 0 | 1 | 0 | 1
S4 | 0 | 1 | 0 | 0 | 0 | 1 | 2
We perform the simplex iterations until the optimal solution is reached. After applying the simplex method, the final tableau is obtained as follows:
| A | B | S1 | S2 | S3 | S4 | RHS
------------------------------------------------------
Z | 0 | 1.8 | 0.2 | -1 | -0.4 | 0.4 | 19.2
------------------------------------------------------
S1 | 0 | 0 | 0 | 1.5 | -1 | 1 | 3
S2 | 1 | 0 | -0.5 | 0.5 | 0.5 | -0.5 | 1.5
A | 1 | 0 | 0.5 | -0.5 | -0.5 | 0.5 | 0.5
S4 | 0 | 0 | 1 | -1 | -1 | 1 | 1
From the final tableau, we can see that the maximum value of Z is 19.2 when A=3.6 and B=1.2. This solution satisfies all the constraints of the problem. The calculations can be verified using any software that solves linear programming problems, which should yield the same optimal solution.
Learn more about linear programming here:- brainly.com/question/30763902
#SPJ11
whats the answer to {4t-t+2}4t−t+2
Answers
Answer:
16t^2 - 4t^2 +8t -t +2
12t^2 +7t +2
\((3t+2)4t - t + 212t^{2} + (8t-t)+212t^{2}+7t+2\)
There ya go
~ Mari
The height of the sail on a boat is 7 feet less than 3 times the length of its base. If the The area of the sail is 68 square feet, find its height and the length of the base.
Answers
Step-by-step explanation:
It is given that,
The height of the sail on a boat is 7 feet less than 3 times the length of its base.
Let the length of the base is x.
ATQ,
Height = (3x-7)
Area of the sail is 68 square feet.
Formula for area is given by :
\(A=lb\\\\68=x(3x-7)\\\\3x^2-7x=68\\\\3x^2-7x-68=0\)
x = 8 feet and x = -3.73 feet
So, length is 8 feet
Height is 3(8)-7 = 17 feet.
So, its height and the length of the base is 17 feet and 8 feet respectively.
Find the value of x. Round to the
nearest tenth.
12
Х
2597
X = ?
Enter

Answers
Answer:
x ≈ 5.1
Step-by-step explanation:
Using the sine ratio in the right triangle
sin25° = \(\frac{opposite}{hypotenuse}\) = \(\frac{x}{12}\) ( multiply both sides by 12 )
12 × sin25° = x , that is
x≈ 5.1 ( to the nearest tenth )
(1 point) in how many ways can 2 ice cream toppings be chosen from 12 available toppings? your answer is :
Answers
Answer:
Below
Step-by-step explanation:
12 C 2 = 12! / ( 10! 2!) = 66 ways
give an example of a function that is differentiable on r with exactly two roots but its derivative has 5 roots. the example can be a graph of a function.
Answers
One possible example is the function \(f(x) = (x+1)(x-2)^{2}(x-3)^{2}\), which has roots at x = -1 and x = 2, but whose derivative \(f'(x) = 2(x-2)(x-3)(3x^2-10x+7)\) has roots at x = 1, \(x = 2 - \sqrt(2)\),\(x = 2 + \sqrt(2)\), x = 5/3, and x = 7/3.
To construct such an example, we need a function whose roots are simple and occur at two distinct points, and whose derivative has multiple roots. One way to do this is to take a function that has multiple roots of high multiplicity, and then perturb it so that some of those roots split into simple roots.
In the example given, we start with the function \(f(x) = (x+1)(x-2)^4(x-3)^4\), which has roots at x = -1, x = 2, and x = 3, each with multiplicity 4. We then perturb the function slightly by replacing one of the factors \((x-2)^4\) with \((x-2)^2\), so that the root at x = 2 splits into two simple roots. This gives us the function \(f(x) = (x+1)(x-2)^2(x-3)^4\), which has roots at x = -1 and x = 2, but whose derivative \(f'(x) = 2(x-2)(x-3)^3(3x-10)\) has five roots, as stated above.
Learn more about derivative here:
https://brainly.com/question/29144258
#SPJ11
Solve the inequality for x: x−1x−2≥0
Answers
Given:
Inequality is
\(\frac{x-1}{x-2}\ge0\)Required:
Solve the inequality.
Explanation:
We have inequality greater than or equal to zero.
So, this can happen only when both numerator and denominator positive or negative.
Fraction will be positive when x less than or equal 1 and when x greater than 2.
So, it is
\((-\infty,1]or(2,\infty)\)Answer:
Hence, option B is correct.
If one of the results is randomly selected, what is the probability that it is a false negative (the test indicates the person does not have the disease when in fact they do)? What does this probability suggest about the accuracy of the test?

Answers
0.0323 is the probability that it is a false negative (the test indicates the person does not have the disease when in fact they do)
What is Probability?It is a branch of mathematics that deals with the occurrence of a random event.
Let A be the event of “Negative Test Result” and B be the event of “subject has the disease”. Now,
the total of results is 120+4+172+13=309
Subject has the disease=120+4=124
P(A and B)=4/309
P(B)=124/309
P(negative test result | subject has the disease)
P(A | B) =P(A and B) / P(B)
=(4 / 309) / (124 / 309)
=4 / 124
=1 / 31
0.0323.
Hence 0.0323 is the probability that it is a false negative (the test indicates the person does not have the disease when in fact they do)
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ5
Solve for the value of P

Answers
Answer:
\(sum \: of \:a ngle \: in \: a \: line \: = 180 \\ 2p + 5 + 3p = 180 \\ 5p + 5 = 180 \\ 5p = 180 - 5 \\ 5p = 175 \\ p = \frac{175}{5} \\ p = 35 \\ thank \: you\)