You and a group of friends wish to start a company. You have an idea, and you are comparing startup incubators to apply to. (Start up incubators hold classes and help startups to contactventure capitalists and network with one another) Assume funding is normally distributed. Incubator A has a 70% success ratio getting companies to survive at least 4 years from inception. The average venture funding of the 57 companies reaching that 4 year mark,is 1.3 million dollars with a standard deviation of 0.6 million Incubator B has a 39% success ratio getting companies to survive at least 4 years from inception. The average venture funding of the 40 companies reaching that 4 year mark,is 1.9 million dollars with a standard deviation of 0.55 millionAre the success ratios significantly different?
Answers
To determine if the success ratios of Incubator A and Incubator B are significantly different, we can perform a hypothesis test.
Let's set up the null and alternative hypotheses as follows:
Null Hypothesis (H0): The success ratios of Incubator A and Incubator B are not significantly different.
Alternative Hypothesis (H1): The success ratios of Incubator A and Incubator B are significantly different.
We can use a significance level (α) of 0.05, which is a common choice.
To test the hypothesis, we can use a two-proportion z-test since we are comparing the success ratios of two groups. The formula for the test statistic is:
z = (p1 - p2) / sqrt(p_hat * (1 - p_hat) * (1/n1 + 1/n2))
where:
p1 and p2 are the success ratios of Incubator A and Incubator B, respectively,
p_hat is the pooled sample proportion,
n1 and n2 are the sample sizes of Incubator A and Incubator B, respectively.
Let's calculate the test statistic and compare it to the critical value to make a decision.
Given:
Success ratio of Incubator A (p1) = 0.70
Sample size of Incubator A (n1) = 57
Success ratio of Incubator B (p2) = 0.39
Sample size of Incubator B (n2) = 40
First, calculate the pooled sample proportion (p_hat):
p_hat = (x1 + x2) / (n1 + n2)
where x1 is the number of successes in Incubator A and x2 is the number of successes in Incubator B. Since we are not given the actual counts, we cannot calculate the exact value of p_hat.
Next, calculate the test statistic (z) using the formula above.
Once we have the test statistic, we can compare it to the critical value from the standard normal distribution at the specified significance level (α) to make a decision.
If the test statistic falls within the rejection region (i.e., it is beyond the critical value), we reject the null hypothesis. If it falls within the acceptance region (i.e., it is within the critical value), we fail to reject the null hypothesis.
Without knowing the actual counts of successes in Incubator A and Incubator B, we cannot perform the calculations to determine if the success ratios are significantly different.
To know more about null hypothesis refer here:
https://brainly.com/question/28920252
#SPJ11
Related Questions
According to Newton's law of cooling (sec Problem 23 of Section 1.1), the temperature u(t) of an object satisfies the differential equation du/dt = -K(u - T) where T is the constant ambient temperature and k is a positive constant. Suppose that the initial temperature of the object is u(0) = u_0 Find the temperature of the object at any time.
Answers
Newton's law of cooling describes how the temperature of an object changes over time in response to the surrounding temperature. The equation that governs this process is du/dt = -K(u - T), where u is the temperature of the object at any given time, T is the constant ambient temperature, and K is a positive constant.
To find the temperature of the object at any time, we need to solve this differential equation. First, we can separate the variables by dividing both sides by (u-T), which gives us du/(u-T) = -K dt. Integrating both sides, we get ln|u-T| = -Kt + C, where C is a constant of integration. Exponentiating both sides, we get u-T = e^(-Kt+C), or u(t) = T + Ce^(-Kt).
To find the value of the constant C, we use the initial condition u(0) = u_0. Plugging in t=0 and u(0) = u_0 into the equation above, we get u_0 = T + C. Solving for C, we get C = u_0 - T. Substituting this value of C into the equation for u(t), we get u(t) = T + (u_0 - T)e^(-Kt).
Therefore, the temperature of the object at any time t is given by u(t) = T + (u_0 - T)e^(-Kt).
According to Newton's law of cooling, the temperature u(t) of an object can be determined using the differential equation du/dt = -K(u - T), where T is the constant ambient temperature, and K is a positive constant. To find the temperature of the object at any time, given the initial temperature u(0) = u_0, we need to solve this differential equation.
Step 1: Separate the variables by dividing both sides by (u - T) and multiplying both sides by dt:
(1/(u - T)) du = -K dt
Step 2: Integrate both sides with respect to their respective variables:
∫(1/(u - T)) du = ∫-K dt
Step 3: Evaluate the integrals:
ln|u - T| = -Kt + C, where C is the constant of integration.
Step 4: Take the exponent of both sides to eliminate the natural logarithm:
u - T = e^(-Kt + C)
Step 5: Rearrange the equation to isolate u:
u(t) = T + e^(-Kt + C)
Step 6: Use the initial condition u(0) = u_0 to find the constant C:
u_0 = T + e^(C), so e^C = u_0 - T
Step 7: Substitute the value of e^C back into the equation for u(t):
u(t) = T + (u_0 - T)e^(-Kt)
This equation gives the temperature of the object at any time t, taking into account Newton's law of cooling, the ambient temperature T, and the initial temperature u_0.
For more information on Newton's law visit:
brainly.com/question/15280051
#SPJ11
Thus, the equation that gives the temperature of the object at any time t, considering the initial temperature u_0 and the ambient temperature T is u(t) = T + (u_0 - T)e^(-Kt).
According to Newton's law of cooling, the temperature u(t) of an object satisfies the differential equation du/dt = -K(u - T), where T is the constant ambient temperature and K is a positive constant.
Given the initial temperature u(0) = u_0, we can solve this differential equation to find the temperature of the object at any time.
To solve the differential equation, we can use separation of variables:
1/(u - T) du = -K dt
Integrate both sides:
∫(1/(u - T)) du = ∫(-K) dt
ln|u - T| = -Kt + C (where C is the integration constant)
Now, we can solve for u(t):
u - T = Ce^(-Kt)
To find the constant C, we use the initial condition u(0) = u_0:
u_0 - T = Ce^(-K*0)
u_0 - T = C
So, our temperature function is:
u(t) = T + (u_0 - T)e^(-Kt)
This equation gives the temperature of the object at any time t, considering the initial temperature u_0 and the ambient temperature T.
Know more about the Newton's law of cooling
https://brainly.com/question/2763155
#SPJ11
What is 2 3 times 2 as a fraction?
Answers
2 × 3 × 2 can be written as 2 × 6, so the answer is 6/1, which is an equivalent fraction to 6.
We can solve this problem by converting the expression into a fraction. First, we need to multiply 2 and 3 together, which gives us 6. Then, we need to multiply this result by 2, so we get 12. Finally, we need to express this result as a fraction. To do this, we put the numerator (12) over the denominator (1). So, the answer is 12/1, which simplifies to 4/32 × 3 × 2 can be written as 2 × 6, so the answer is 6/1, which is an equivalent fraction to 6
Learn more about fraction here
https://brainly.com/question/10354322
#SPJ4
What is the surface area of the right rectangular prism below? 25030 A. 130 in.2 B. 154 in.2 C. 308 in.2 D. 312 in.2
Answers
Answer:
Do you have a picture? Or any of the measurements?
please help, i got a 0% ! screenshot of the assignment is attatched

Answers
Answer:
24 units squared
Step-by-step explanation:
Remember, it's the surface area: count the squares that are in the shape. 24 is the answer.
Answer:
24
Step-by-step explanation:
A=6a2 is the formal you need to salve for the aria of a cube
4) easy- solve for x

Answers
Answer: - 8
Step-by-step explanation:
x/4 - 5 = -7
=> x/4 = -2
=> x = -8
Answer:
x=−8
Step-by-step explanation:
Add 5 to both sides
x/4-5+5=-7+5
x/4=-2
4x/4=4(-2)
x=-8
Tyler has saved $1,000. He earns $16 an hour. Tyler saves 25 percent of his net pay, after 20 percent is taken out for taxes. Which statements are correct? A) Tyler has to work 312.5 hours to double his savings. B) Tyler adds $3.20 to his savings for every hour he works. C) The explicit expression for this situation is 3.2x + 1000. D) Tyler will have to work 625 hours to have $4,000 in savings. E) This situation can be expressed recursively as Sn = Sn-1 − 3.2, S0 = 1000.
Answers
Answer:
The answer is A, B and C
Step-by-step explanation:
I did the USATestprep thingy
el cuadro de un numero natural menos nueve es igual a 315. ¿ cual es ese numero ?
Answers
Answer:
Espanol? or english?
Step-by-step explanation:
a simple random sample of 5 observations from a population containing 400 elements was taken, and the following values were obtained: 15, 19, 21, 24, and 31. a point estimate of the mean is
Answers
The point estimate of the population mean is 22.
How to determine point estimate?A simple random sample of 5 observations from a population containing 400 elements was takenthe following values were obtained:
15, 19, 21, 24, and 31.
A simple random sample is a sampling technique that chooses n elements from a population of size N in such a way that each possible sample of the same size n is equally likely to be chosen.
The point estimate of the population mean can be calculated as the sample mean, which is the sum of the observations divided by the sample size:
Sample mean = (15 + 19 + 21 + 24 + 31) / 5
= 110 / 5
= 22
Therefore, the point estimate of the population mean is 22
Learn more about point estimate
brainly.com/question/30057704
#SPJ11
Regular hexagon ABCDEF is inscribed in a circle with center H. What is the image of segment BC after 120 degree clockwise rotation about point H?
Answers
Regular hexagon ABCDEF is inscribed in a circle with center H, the image of segment BC after 120 degree clockwise rotation about point H is the segment joining the points B' and C', which has endpoints (-0.5r\(\sqrt{3\), -0.5r) and (-0.5r, -0.5r).
Since the hexagon is inscribed in a circle with center H, we can conclude that H is also the center of the circle passing through vertices B, C, and D. Therefore, the circle passing through B, C, and D is also a 120 degree clockwise rotation of the circle passing through A, B, and C.
To find the image of segment BC after a 120 degree clockwise rotation about point H, we need to find the coordinates of B and C relative to H, and then apply a 120 degree rotation matrix to these coordinates.
Let the radius of the circle be r, and let the coordinates of H be (0,0). Then the coordinates of B and C are:
B: (r cos(60), r sin(60))
C: (r cos(0), r sin(0)) = (r, 0)
To apply a 120 degree clockwise rotation matrix, we can use the following matrix:
[ cos(-120) -sin(-120) ]
[ sin(-120) cos(-120) ]
Simplifying, we get:
[ cos(120) sin(120) ]
[ -sin(120) cos(120) ]
Applying this matrix to the coordinates of B and C, we get:
B': [ cos(120) sin(120) ][ r cos(60) ] = [ -0.5r \(\sqrt{3}\)]
[ -sin(120) cos(120) ][ r sin(60) ] [ -0.5r ]
C': [ cos(120) sin(120) ][ r ] = [ -0.5r ]
[ -sin(120) cos(120) ][ 0 ] [ -0.5r ]
Therefore, the image of segment BC after a 120 degree clockwise rotation about point H is the segment joining points B' and C', which has endpoints (-0.5r\(\sqrt{3}\), -0.5r) and (-0.5r, -0.5r), respectively.
To know more about Hexagon:
https://brainly.com/question/2001860
#SPJ4
What are the three unbiased estimators?
Answers
The three unbiased estimators are the sample mean, sample variance, and sample proportion. These estimators provide unbiased estimates of the population mean, population variance, and population proportion, respectively.
There are several unbiased estimators commonly used in statistics, but three notable examples are the sample mean, the sample variance, and the sample proportion.
1. Sample Mean: When estimating the population mean, the sample mean is an unbiased estimator. It is calculated by taking the average of all the observations in a sample. Under certain conditions, such as random sampling, the sample mean provides an unbiased estimate of the population mean.
2. Sample Variance: When estimating the population variance, the sample variance is an unbiased estimator. It measures the dispersion of the data points around the sample mean. By dividing the sum of squared differences by the sample size minus one, the sample variance provides an unbiased estimate of the population variance.
3. Sample Proportion: When estimating the population proportion, the sample proportion is an unbiased estimator. It represents the proportion of a specific characteristic or outcome within a sample. If the sample is obtained randomly and meets certain conditions, the sample proportion provides an unbiased estimate of the population proportion.
These three unbiased estimators play crucial roles in statistical inference, allowing researchers to make inferences about population parameters based on sample data.
To know more about unbiased estimator, refer here:
https://brainly.com/question/14273393#
#SPJ11
Solve for x. Round to the nearest tenth of a degree, if necessary.
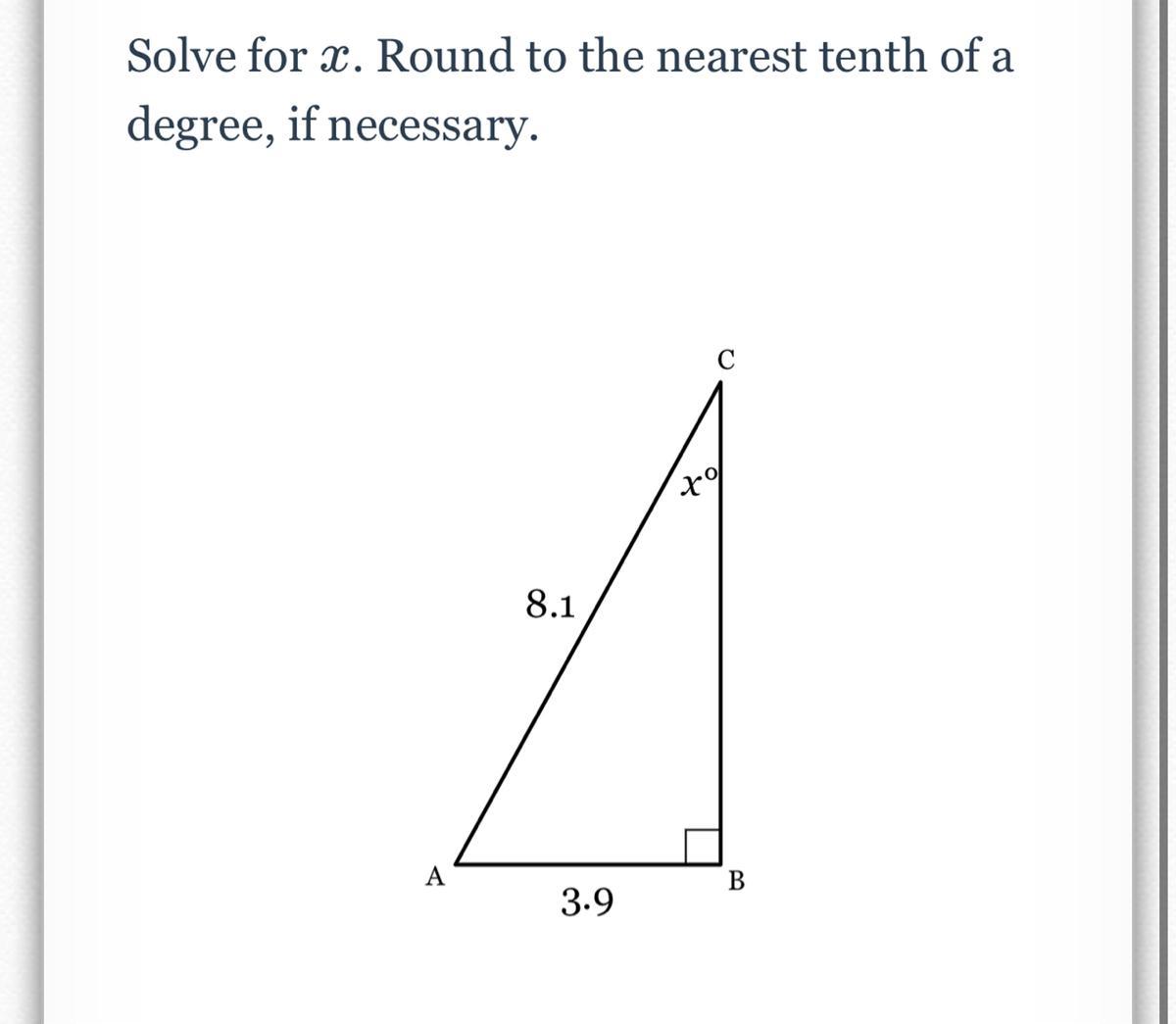
Answers
Answer:
x ≈ 28.8°
Step-by-step explanation:
Using the sine ratio in the right triangle
sin x = \(\frac{opposite}{hypotenuse}\) = \(\frac{AB}{AC}\) = \(\frac{3.9}{8.1}\) , then
x = \(sin^{-1}\) (\(\frac{3.9}{8.1}\) ) ≈ 28.8° ( to the nearest tenth )
whats 750 centimeters to meters
Answers
Lines EC and HF are parallel CDG is congruent to dgh what is the measure of CDG

Answers
Same side interior angles are =180
2x+4x-30=180
6x-30=180
6x=210
x=35
CDG is congruent to DGH(alternate interior)
4x-30
4(35)-30
140-30
=110
A box has 2θ+1 balls, marked consecutively as −θ,−(θ−1),…,−1,0,1,…,(θ− 1), θ, where θ≥10 is an unknown integer. (So, we know that the box contains at least 21 balls, but not the exact number.) Suppose 20 balls are selected at random and without replacement and the marks on the selected balls, denoted X 1
,…,X 20
are recorded. (a) Find a statistic that is minimal sufficient for θ and derive its distribution. (b) Is the minimal sufficient statistic in (a) also complete.
Answers
Yes, the minimal sufficient statistic is also complete, because the distribution of T depends on θ, and the mean of any function of T is a function of θ. Therefore, any unbiased estimator of zero is also an unbiased estimator of E [g (T)] = ∑ g (t) P (T = t | θ), which is a function of θ.
A statistic that is minimal sufficient for θ and derive its distribution:
Let n = 2θ + 1 be the total number of balls in the box.
Let x1, x2, x20 be the marks on the selected balls.
The number of ways to select 20 balls is (n choose 20).
Let y1, y2, y20 denote the positions of the selected balls.
Then y1 < y2 < < y20, and the number of ways to select the positions is (n choose 20).
Thus, the likelihood function is given by
L(θ) = (n choose 20) 1 [(θ + y 20 - x 20) (θ + y19 - x19) (θ + y1 - x1)] [(θ - y1 + x1) (θ - y2 + x2) (θ - y20 + x20)]
For fixed x1, x2, ..., x20, the ratio of the likelihood functions for two different values of θ depends only on the product of the terms with θ in each of the two factors, so the likelihood function depends only on ∏ (θ + y - x) and ∏(θ - y + x). The factorization theorem implies that T = X (1) - X (20) is a minimal sufficient statistic for θ. To see this, note that the ratio of the likelihood functions for two different values of θ depends only on the ratio of the products of the terms with θ in each of the two factors, so the likelihood function depends only on T = X (1) - X (20).
It follows that the conditional distribution of X (1), X (20), given T, does not depend on θ, so the distribution of T does not depend on θ either. For fixed T, the likelihood function is proportional to
∏ (θ + y - x) and ∏ (θ - y + x), and these factors are both decreasing functions of θ, so the maximum likelihood estimator of θ is the smallest value of θ that is consistent with the observed values of X (1) and X (20), namely X (1) - T and X (20) + T.(b)
Yes, the minimal sufficient statistic is also complete, because the distribution of T depends on θ, and the mean of any function of T is a function of θ. Therefore, any unbiased estimator of zero is also an unbiased estimator of E [g (T)] = ∑ g (t) P (T = t | θ), which is a function of θ.
To know more about statistic visit:
brainly.com/question/31577270
#SPJ11
Lily convinced her parents to have her birthday party at Flyzone Trampoline park. As soon as she gets there , lily spends 3/4 of an hour eating birthday cake with her friends in all , lily spends 2 1/4hours at Fly zone .
Answers
Answer: 1.5 hours
Step-by-step explanation:
I assume you’re trying to find how much time she is doing other activity.
2 1/4 - 3/4 is equal to:
2.25-0.75
That equals 1.5.
Find the area of triangle STU
Help me

Answers
Answer:
12cm cubed
Step-by-step explanation:
A= base*height/2 so base is 6 just count the squares and height is 4 at the highest point so just plug those in the formula hopefully its correct
Step-by-step explanation:
The height is 5
and the base is 7
area of triangle = bxh
= 7 x 5
= 35 cm2
What would the number of sides be on a polygon with an interior angle of 176 degrees
Answers
The number of sides on a polygon with an interior angle of 176 degrees would be 10.
Here's how you can solve it:
To find the number of sides in a polygon, we need to use the formula below:
(n - 2) × 180° / n = Interior
Angle where n is the number of sides in a polygon and Interior
Angle is the angle in the polygon.
To solve for n in this formula, we need to use the given angle.
So, we can rearrange the formula as shown below:
n = (Interior Angle × n) / (n - 2)
We know that the given Interior Angle is 176 degrees.
Substituting this value in the above formula, we get:
n = (176 × n) / (n - 2)
Multiplying both sides by n - 2, we get:n(n - 2) = 176n
Expanding the left-hand side of the equation:n² - 2n = 176n
Rearranging the equation to solve for n:n² - 178n = 0n(n - 178) = 0
So, n = 0 or n = 178.
But we can discard n = 0
because the number of sides of a polygon can't be zero.
Hence, n = 178 is the extraneous solution that we can discard.
The correct solution is:n = 10
Therefore, the number of sides on a polygon with an interior angle of 176 degrees is 10.
To know more about polygon, visit:
https://brainly.com/question/23846997
#SPJ11
GEOMETRY FIND LENGTH OF THIRD SIDE!!

Answers
Answer:
Below
Step-by-step explanation:
I previously answered this Q here:
https://brainly.com/question/30162460
-1/8n= -2/7 whats the n value?
Answers
Answer:
16 /7
Step-by-step explanation:
multiply both sides by -8 then simplify
Please help on both! And please put answer and not a website!

Answers
Answer:
1: 55 2: 40
Step-by-step explanation:
For the first problem, by the triangle angle theorm, the three angles in a triangle add up to 180, so
90+35+x=180
125 + x = 180
x = 55
Now, the angle you just found (x = 55) and the exterior angle are supplementary so they also add up to 180
55 + y = 180
y = 125
For the second problem, the two angles in a triangle non-adjacent to the exterior angle are equal to the exterior angle, so
40 + 2x = 3x
x = 40
how come when i have an American flag people hate but when somebody has a pride flag everybody love them?
Answers
what is the coefficient of (3y^2 + 9)5
Answers
The coefficient of (3y² + 9)5 is 15.
A polynomial is of the form a₀xⁿ + a₁xⁿ⁻¹ + a₂xⁿ⁻² + ... + aₙ₋₁x + aₙ.
Here, x is the variable, aₙ is the constant term, and a₀, a₁, a₂, ..., and aₙ₋₁, are the coefficients.
a₀ is the leading coefficient.
In the question, we are asked to identify the coefficient of (3y² + 9)5.
First, we expand the given expression:
(3y² + 9)5
= 15y² + 45.
Comparing this to the standard form of a polynomial, a₀xⁿ + a₁xⁿ⁻¹ + a₂xⁿ⁻² + ... + aₙ₋₁x + aₙ, we can say that y is the variable, 15 is the coefficient, and 45 is the constant term.
Thus, the coefficient of (3y² + 9)5 is 15.
Learn more about the coefficients of a polynomial at
https://brainly.com/question/9071229
#SPJ1
which rectangle has side lengths of 5 units and 4 units?
A) A(3,3), B(3,6), C(8,6), D(8,3)
B) A(3,3), B(3,7), C(8,7), D(8,3)
C) A(3,3), B(3,7), C(7,7), D(7,3)
D) A(3,3), B(3,8), C(8,8), D(8,3)
Answers
The rectangle that has side lengths of 5 units and 4 units is C) A(3,3), B(3,7), C(7,7), D(7,3).
Point C at (7,7), means the width is 4 units (7-3) and the height is 5 units (7-2), so this is the correct rectangle.
What is a rectangle?A rectangle is a shape with four right angles (that is four angles of 90 degrees) and the opposite sides are parallel and congruent.
The two sides of a rectangle are parallel and they meet at the four corners or vertices.
For a rectangle, the opposite sides are of the same length and are parallel to each other.
Therefore, C. A(3,3), B(3,7), C(7,7), D(7,3) is the rectangle that has side lengths of 5 units and 4 units.
Read more about a rectangle at brainly.com/question/25292087
#SPJ1
what is the test statistic does not fall in the rejection region when a false null hypothesis is being tested?
Answers
If a test statistic does not fall in the rejection region when a false null hypothesis is being tested, it means that the null hypothesis cannot be rejected at the chosen level of significance.
In hypothesis testing, the rejection region is the set of all possible test statistic values that are unlikely to occur if the null hypothesis is true. If the test statistic falls within this region, then the null hypothesis is rejected in favor of the alternative hypothesis.
However, if the test statistic falls outside the rejection region, it means that the observed data is consistent with the null hypothesis. In other words, the data does not provide enough evidence to reject the null hypothesis at the chosen level of significance.
To know more about test statistic:
https://brainly.com/question/14128303
#SPJ4
Please help me out with this one

Answers
Answer:
The slope of the line = m = 3
Step-by-step explanation:
Given the table
x 3 6 8 12
y 7 16 22 34
Taking any two points let say (3, 7) and (6, 16)
(x₁, y₁) = (3, 7) (x₂, y₂) = (6, 16)Using the formula
Slope = m = [y₂ - y₁] / [x₂ - x₁]
= [16 - 7] / [6 - 3]
= 9 / 3
= 3
Therefore, the slope of the line = m = 3
In a class of students, the following data table summarizes how many students play
an instrument or a sport. What is the probability that a student chosen randomly
from the class plays a sport?
Plays a sport
Does not play a sport
Plays an instrument Does not play an instrument
3
8
10
9
Answers
Answer:
3 OR 8 hope this helps!
Step-by-step explanation:
Please help asap thx :)

Answers
Step-by-step explanation:
the average rate of change is
(f(x2) - f(x1)) / (x2 - x1)
so, for x = 1 and 2
(4×3² - 4×3¹) / (2 - 1) = 36 - 12 = 24
for x = 3 and 4
(4×3⁴ - 4×3³) / (4 - 3) = 324 - 108 = 216
so the second rate is 216/24 = 9 times greater than the first rate.
How did the judge find out about the rotten milk?
Answers
Please help. What is the answer to the Algebra 2 question

Answers
Answer:
(- ∞,1]
Step-by-step explanation:
15. The length of Yvette's cell phone screen is 0.35 feet. A movie theater screen is
about 100 times longer than Yvette's cell phone screen. What is the approximate
length of the movie theater screen?
Answers
Answer:
it would 35 feet long 100x0.35
The length of the movie theater will be 35 feet.
What is algebraic expression?In mathematics, an algebraic expression is an expression built up from constant algebraic numbers, variables, and the algebraic operations. For example, we can write the expressions as -
2x + 3y + 5
3y + 5
5 + 6
Given is that the length of Yvette's cell phone screen is 0.35 feet. A movie theater screen is about 100 times longer than Yvette's cell phone screen.
Scale factor is defined as the ratio of final dimensions to the initial dimensions of the given image.
Mathematically, we can write -
{K} = final dimensions/initial dimensions
In the question given, the scale factor is -{K} = 100.
Assume the length of the movie theater to be {x}. So, we can write -
{x} = 0.35 x 100
{x} = 35/100 x 100
{x} = 35 feet
Therefore, the length of the movie theater will be 35 feet.
To solve more questions on algebraic expression , visit the link below -
brainly.com/question/27911936
#SPJ6