y= A(0.5)^t/(half-life) What is half-life
Answers
The half-life is the amount of time it takes for a quantity to reduce to half its initial value.
In the equation y = A(0.5)^(t/half-life), the half-life is represented as a variable in the denominator of the exponent.
y is the final value of the quantity after a certain amount of time, t.
A is the initial value of the quantity at the beginning (t = 0).
0.5 is the factor that represents a 50% decrease, as we are considering half-life.
t is the time that has passed.
half-life is the time it takes for the quantity to reduce to half its initial value.
In this equation, the half-life is used to determine how much of the initial quantity (A) remains after a certain amount of time (t). By dividing t by the half-life in the exponent, we can calculate the remaining quantity (y) after the specified time.
More on half-life: https://brainly.com/question/24710827
#SPJ11
Related Questions
The standard length of a piece of cloth for a bridal gown is 3.25 meters. A customer selected 35 pcs of cloth for this purpose. A mean of 3.52 meters was obtained with a variance of 0.27 m2 . Are these pieces of cloth beyond the standard at 0.05 level of significance? Assume the lengths are approximately normally distributed
Answers
The pieces of cloth are beyond the standard at 0.05 level of significance.
We can use a one-sample t-test to determine if the mean length of the 35 pieces of cloth is significantly different from the standard length of 3.25 meters.
The null hypothesis is that the mean length of the cloth pieces is equal to the standard length:
H0: μ = 3.25
The alternative hypothesis is that the mean length of the cloth pieces is greater than the standard length:
Ha: μ > 3.25
We can calculate the test statistic as:
t = (x - μ) / (s / √n)
where x is the sample mean length, μ is the population mean length (3.25 meters), s is the sample standard deviation (0.52 meters), and n is the sample size (35).
Plugging in the values, we get:
t = (3.52 - 3.25) / (0.52 / √35) = 3.81
Using a t-table with 34 degrees of freedom (n-1), and a significance level of 0.05 (one-tailed test), the critical t-value is 1.690.
Since our calculated t-value (3.81) is greater than the critical t-value (1.690), we reject the null hypothesis and conclude that the mean length of the 35 pieces of cloth is significantly greater than the standard length at the 0.05 level of significance.
Know more about level of significance here:
https://brainly.com/question/30542688
#SPJ11
The formula e^2Ïiâ1=0 follows from Euler's formula.
a. true b. false
Answers
Given points A(-1,4) and B(x,7), determine the value(s) of x if AB=5cm
Answers
The value of x is either 3 or -5 based on the distance formula.
What is a co-ordinate system?
In pure mathematics, a coordinate system could be a system that uses one or additional numbers, or coordinates, to uniquely confirm the position of the points or different geometric components on a manifold like euclidean space.
Main body:
according to question
Given points A(-1,4) and B(x,7)
Also AB = 5 cm
Formula of distance = \(\sqrt{(y1-y2)^{2}+(x1 -x2)^{2} }\)
here by using points ,
5 = \(\sqrt{(x+1)^{2} +(7-4)^{2} }\)
taking square on both side ,'
25 = \((x+1)^{2} +3^{2}\)
25-9 = (x+1)²
16 = (x+1)²
taking square root on both sides,
x+1= ±4
x = 4-1 = 3 or x = -4-1 = -5
Hence value of x is either 3 or -5.
To know more about point , visit:
https://brainly.com/question/26310043
#SPJ1
The value of the expression a³-2a²+3a+5 for a = -1
Answer quickly.
Will mark the correct answer as brainliest.
Answers
Answer:
- 1
Step-by-step explanation:
Substitute a = - 1 into the expression, that is
(- 1)³ - 2(- 1)² + 3(- 1) + 5
= - 1 - 2(1) - 3 + 5
= - 1 - 2 - 3 + 5
= - 6 + 5
= - 1
Answer:
=(-1)³-2(-1)²+3(-1)+5
=-1-2(1)+3(-1)+5
=-1-2+3+5
=-3+8
=5
Expand
True or False
sin( x - pi/2 ) = cos x
Answers
Answer:
hola le noeva si (true) neisa adios
Convert 5 6/7 into an
into an improper fraction.
Answers
Answer:
41/7
Step-by-step explanation:
You first should multiply the denominator, which is 7, by the whole number part, five, and add the numerator, six, to get the new numerator. Then you place the new number, 41, over the old denominater which leaves you with 41/7.
The mixed fraction 5 6/7 can be converted in to the improper fraction as 41/7.
Given a mixed fraction,
5 6/7
We have to convert this in to improper fraction.
Improper fractions are fractions which contains the numerator which is greater then the denominator.
All improper fractions can be converted in to mixed fraction and vice versa.
Here fraction is 5 6/7.
5 6/7 = 5 + 6/7
Cross multiplying,
5 6/7 = [(5 × 7) + 6] / 7
= (35 + 6)/7
= 41/7
Hence the improper fraction is 41/7.
Learn more about Mixed fractions here :
https://brainly.com/question/28957298
#SPJ6
Find the distance between point P and line ℓ.
Line ℓ contains points (0, −3 ) and (7, 4). Point P has coordinates (4, 3).
Answers
The distance between the line containing the points (0,-3) and (7,4) and the point P(4,3) is d =√2 units.
What is the distance between a line and a point?The distance between the line ax +by +c =0 and the point (x₁, y₁) is given by:
\(d=\frac{|ax_{1}+by_{1}+c|}{\sqrt{a^2+b^2}}\)
Given that, the line passes through the points (0,-3) and (7,4).
The equation of the line is given by:
\(y -(-3)=\frac{4-(-3)}{7-0}(x-0)\\\\y+3=x\\\\x-y-3=0\)
Now, the distance between the line x - y - 3 = 0 and point (4,3) is:
\(d=\frac{|1\times4+(-1)\times3+(-3)|}{\sqrt{1^2 +(-1)^2}}\\\\d=\frac{2}{\sqrt{2}}\\\\d=\sqrt{2}\)
Hence, the distance between the line containing the points (0,-3) and (7,4) and the point P(4,3) is d =√2 units.
Learn more about the distance between a line and a point:
https://brainly.com/question/11558698
#SPJ1
solve the following quadratic equation by using formula method.√2x² + 4x + 2√2 = 0
Answers
Answer:
(3+2)+(4+2)
Step-by-step explanation:
234
PlZ HELP ME ITS URGENT
A.cannot be determined
B.47°
C.63°
D.70°

Answers
Answer:
C.
Step-by-step explanation:
the second answer is correct
Answer:
C. 63 degrees
Step-by-step explanation:
When 2 triangles are congruent, no matter what postulate they are congruent by, all their sides and angles will be congruent.
We know that triangle ABC is congruent to triangle DEF. Their angles and sides are congruent and corresponding.
We know that angle A is 70 degrees, angle B is 47 degrees and angle C is 63 degrees.
Angle C and angle F correspond. Therefore, angle C and angle F are congruent. Angle C is 63 degrees, therefore angle F must be 63 degrees.
C. 63 degrees is the correct answer.
What is the opposite of 67?
Answers
Answer:
-67 I belive
Step-by-step explanation:
Answer:
normally I'd make a joke and say 76 but the answer would be -67 lol
Step-by-step explanation:
Draw a line representing the "rise" and a line representing the "run" of the line. State
the slope of the line in simplest form.
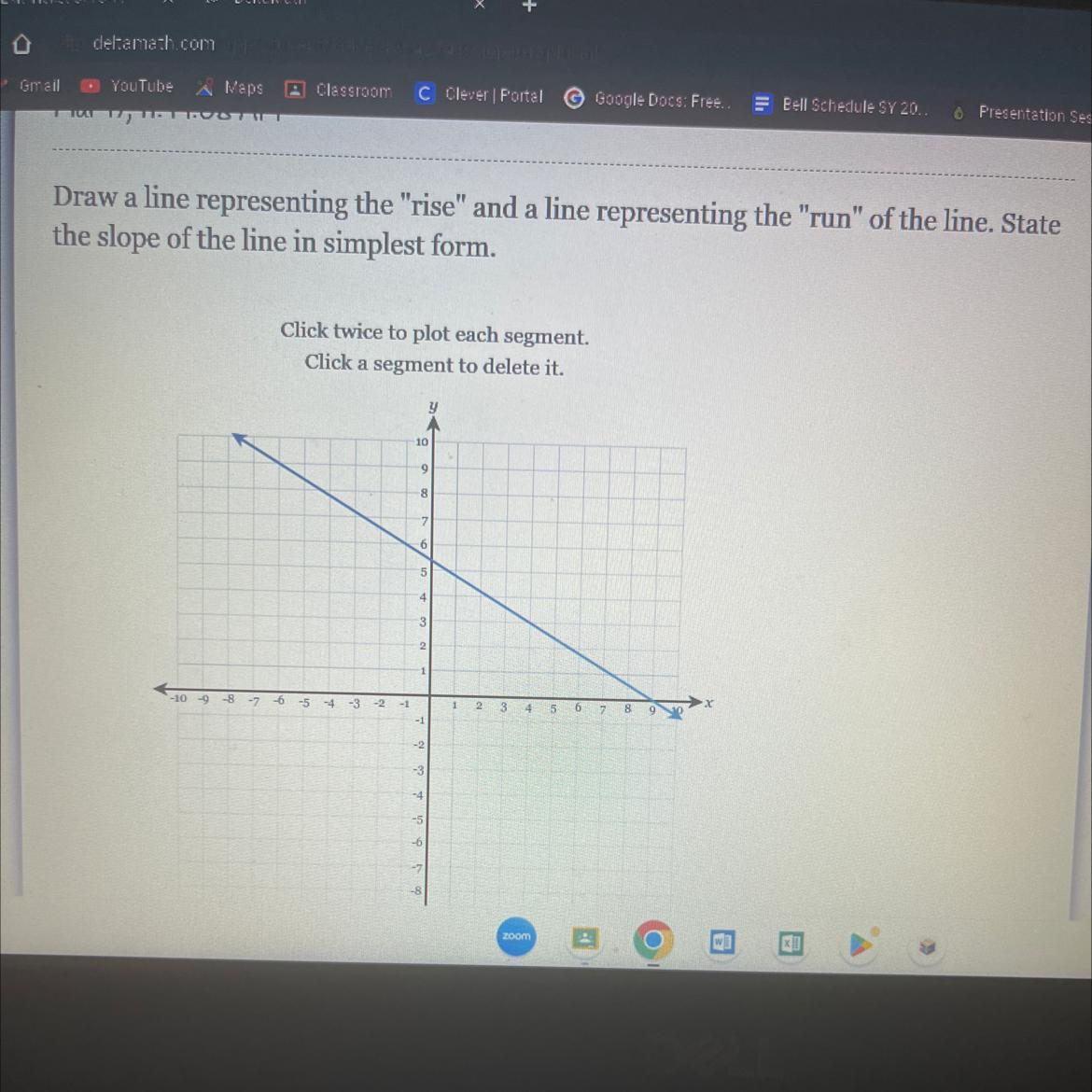
Answers
Answer:yo
Step-by-step explanation:
I need this question solved with derivatives please:
A rectangular piece of cardboard, 100 cm by 40 cm, is going to be used to
make a rectangular box with an open top by cutting congruent squares from
the corners. Calculate the dimensions (to one decimal place) for a box with
the largest volume.
Answers
Answer:
16,242. 7 cm^3.
Step-by-step explanation:
We need to cut off a square piece at the 4 corners of the cardboard.
Let the length of their edges be x cm.
The volume of the box will be:
V = height * width * length
V = x(100-2x)(40-2x)
V = x(4000 - 200x - 80x + 4x^2)
V = x(4x^2 - 280x + 4000)
V = 4x^3 + - 280x^2 + 4000x
Finding the derivative:
dV / dx = 12x^2 - 560x + 4000 = 0 ( when V is a maxm or minm.)
4(3x^2 - 140x + 1000) = 0
x = 37.86, 8.80.
Looks like x = 8.80 is the right value but we can check this out be looking at the sign of the second derivative:
V" = 24x - 560, when x = 8.8 V" is negative so this is a Maximum for V.
So the maximum volume of the box is when x = 8.8 so we have
V = 8.8(100-2(8.8)(40 - 2(8.8)
= 16,242. 7 cm^3.
(15 POINTS!!!) Solve 4 two-step equations:
1. 2x + 12 = 4
2. -5c + 9 = -16
3. -12 = -7 + x/4 (<-- x divided by 4)
4. -n/6 + 4 = 3
Answers
2. C=5
3. X= -20
4. N= 6
What is the value of (3x10^-3
Answers
Answer:
0.003 or 3/1000
Step-by-step explanation:
john and jane go rock-climbing together. john climbs a height of $(x 5)$ miles in $(x-1)$ hours and jane climbs a height of $(x 11)$ miles in $(x 1)$ hours. if john and jane were climbing at the same speed, what must have been their speed, in miles per hour?
Answers
Given that John climbs a height of \($(x + 5)$\) miles in \($(x - 1)$\) hours and Jane climbs a height of \($(x + 11)$\) miles in \($(x + 1)$\) hours. We know that the distance covered by both John and Jane are equal.
Distance covered by John = Distance covered by Jane
Therefore, \($(x + 5) = (x + 11)$\)
Thus, x = 6
Now, we need to find the speed of both, which is given by the formulae:
Speed = Distance / Time
So, speed of John = \($(x + 5) / (x - 1)$\) Speed of John =\($11 / 5$\) mph
Similarly, speed of Jane = \($(x + 11) / (x + 1)$\)
Speed of Jane = \($17 / 7$\) mph
Since both have to be equal, Speed of John = Speed of Jane Therefore,
\($(x + 5) / (x - 1) = (x + 11) / (x + 1)$\)
Solving this equation we get ,x = 2Speed of John = \($7 / 3$\) mph
Speed of Jane = \($7 / 3$\) mph
Thus, their speed was \($7 / 3$\) mph.
To know more about distance visit:
https://brainly.com/question/15172156
#SPJ11
Two large high schools in a city (3000 students in each school) claim they have a higher rate of students who go on to graduate from a 4-year university. 57% of students from school A go on to graduate from a 4 year university and 61% from school B. A random sample of 75 students from school A and 80 from school B are selected and followed to determine if they graduate from a 4-year university.
a. Find the probability that difference in sample proportions is more than 6.
b. What is the probability that School A sample proportion is more than 5% higher than School B?
Answers
a. The probability that difference in sample proportions is more than 6% is 0.1056.
b. There is a 0.2677 probability that the sample proportion from School A is greater than 5% than that from School B.
a. We must first determine the standard error of variation between the two sample proportions in order to determine the probability that the difference in sample proportions is greater than 6:
SEp1-p2 = sqrt{ [p1(1-p1)/n1] + [p2(1-p2)/n2] }
where,
P1 = 57% of students are from school A.
p2 = 61% of students are from school B.
Sample sizes from schools A and B were 75 and 80, respectively.
SEp1-p2 = sqrt{ [(0.57)(0.43)/75] + [(0.61)(0.39)/80] }
= sqrt{ 0.00233 + 0.00240 }
= 0.0803
Now, we can find the Z-score as:
Z = (p1 - p2 - D) / SEp1-p2
where,
D = 6% = 0.06
Z = (0.57 - 0.61 - 0.06) / 0.0803
= -1.248
Using a standard normal distribution table, we can find the probability that Z < -1.248 is 0.1056.
Therefore, the probability that difference in sample proportions is more than 6% is 0.1056.
b. To find the probability that School A sample proportion is more than 5% higher than School B, we need to find the standard error of the difference between the two sample proportions:
SEp1-p2 = sqrt{ [p1(1-p1)/n1] + [p2(1-p2)/n2] }
where,
57% of the population in p1 is from school A.
61% of those in p2 are from school B.
75 were included in the sample from school A, while 80 were included in the sample from school B.
SEp1-p2 = sqrt{ [(0.57)(0.43)/75] + [(0.61)(0.39)/80] }
= sqrt{ 0.00233 + 0.00240 }
= 0.0803
Now, we can find the Z-score as:
Z = (p1 - p2 - D) / SEp1-p2
where,
D = 5% = 0.05
Z = (0.57 - 0.61 - 0.05) / 0.0803
= -0.621
We can get the probability that Z -0.621 is 0.2677 by using a standard normal distribution table.
Know more about Probability here:
https://brainly.com/question/32117953
#SPJ11
g(x)=2x-8, f(x)=5-g(x) what is the value of f(10)
Answers
By evaluating the function, we conclude that f(10) = -7
How to evaluate the function f(x)?
Here we know that:
g(x) = 2x - 8
And f(x) = 5 - g(x).
Then we can write:
f(x) = 5 - (2x - 8) = 5 - 2x + 8 = -2x + 13
Now we want ot evaluate it in x = 10, this means replace the variable by the number 10.
f(10) = -2*10 + 13 = -20 + 13 = -7
Then, we conclude that f(10) = 7
If you want to learn more about evaluating:
https://brainly.com/question/1719822
#SPJ1
AMC 10/12 Student Practice Questions
Guide to Student Practice Questions
Each of the following four large congruent squares is
subdivided into combinations of congruent triangles or
rectangles and is partially shaded. What percent of the total
area is partially shaded?
I
The original problem
and choices from the
2011 AMC 8 contest
(A) 12 (B) 20
(C) 25 (D) 33 (E) 37

Answers
Answer:
\(\mathrm{C.\:}25\)
Step-by-step explanation:
Notice how each congruent square is divided into four equal parts. Since each square has four parts and there are four squares, there are \(16\) of these parts in total. Because each of these parts make up \(\frac{1}{4}\) of each square, all parts are equal. Therefore, you can count the total number of shaded parts to get your percentage.
The top left and bottom right both have one part shaded each for a total of \(2\) parts.
The top right and bottom left have \(0.5\) and \(1.5\) parts shaded, respectively, for a total of \(2\) parts.
Therefore, in total, there are \(2+2=4\) parts shaded out of \(16\) total parts.
Thus, the percentage of the total area that is shaded is:
\(\frac{4}{16}=\frac{1}{4}=\fbox{$25\%$}\).
a factory makes rods by cutting plastic pipes that are 4 feet long into 7 equal sized rodshow long is each rod?what is the total length of 15 rods?
Answers
As a fraction, length of the 15 rods = 8 4/7 feet
As decimal, length = 8.57 feet
Explanation:initial length pipes = 4 feet
Dividing the length of the pipe into 7:
\(\begin{gathered} length\text{ }of\text{ each rod = }\frac{initial\text{ length}}{7\text{ parts}} \\ length\text{ }of\text{ each rod }=\frac{4}{7}\text{feet} \end{gathered}\)length of 15 of those rods:
\(\begin{gathered} \text{length = 15 }\times\text{ length of each rod} \\ \text{length = 15 }\times\text{ }\frac{4}{7} \end{gathered}\)\(\begin{gathered} length\text{ of 15 rods = }\frac{60}{7} \\ Total\text{ length of 15 rods = 8}\frac{4}{7}\text{ or 8.57 f}eet \end{gathered}\)What is -3/8 times (-1/7)?
Answers
PLEASE HURRY! How many one-half cubes with dimensions of One-half times 1 times 1 fit in a unit cube? 1 2 4 6
Answers
Answer: I think its 2
Step-by-step explanation:
Answer:
2
Step-by-step explanation:
volume of the unit cube:
V = 1 * 1 * 1 = 1
volume of the half-cube:
V = 1/2 * 1 * 1 = 1/2
number of half cubs that fit in unit cube:
1/(1/2) = 2
Answer: 2
There are 20 people trying out for a team. How many ways can you make randomly select for people to make a team?
Answers
There are 15,504 ways to randomly select a team of 5 people from a group of 20 people
If there are 20 people trying out for a team, the number of ways to select a team of n people can be calculated using the formula for combinations, which is:
C(20, n) = 20! / (n! * (20 - n)!)
where C(20, n) represents the number of ways to select n people from a group of 20 people.
For example, if we want to select a team of 5 people, we can plug in n = 5 and calculate:
C(20, 5) = 20! / (5! * (20 - 5)!) = 15,504
Therefore, there are 15,504 ways to randomly select a team of 5 people from a group of 20 people. Similarly, we can calculate the number of ways to select teams of different sizes by plugging different values of n into the formula for combinations.
Learn more about randomly
https://brainly.com/question/4013322
#SPJ4
Find the slope of the line containing the points (4,8) and (4,6) then find the slope of a line parallel to this line and the slope of the line perpendicular to this line.
Answers
To calculate the slope between 2 points we use the following equation:
\(m=\frac{y_2-y_1}{x_2-x_1}\)Replacing the points:
\(\begin{gathered} m=\frac{8-6}{4-4} \\ m=\frac{2}{0} \\ m\to\infty \end{gathered}\)In this case, when we find an infinite slope, it means that it is a line parallel to the Y axis. All parallel lines have the same slope.
For the perpendicular case, the slope is equal to:
\(\begin{gathered} m_{\perp}=\frac{1}{m} \\ m_{\perp}=\frac{1}{\frac{2}{0}} \\ m_{\perp}=\frac{0}{2} \\ m_{\perp}=0 \end{gathered}\)For the perpendicular case, the slope is zero and would equal one parallel to the X axis.
Answer:
not definednot definedzeroStep-by-step explanation:
The question is asking us to find the slope.
First, we will find the slope of the line that passes through (4,8) and (4,6).
We'll use the slope formula:
\(\bf{m=\dfrac{y_2-y_1}{x_2-x_1}}\)
Plug in the data :
\(\bf{m=\dfrac{6-8}{4-4}}\)
\(\bf{m=\dfrac{-2}{0}}\)
\(\bf{m=not\:de fined}\)
If a line's slope is not defined, then it's a vertical line:
\(\rule{1}{350}\)
------
Now, what is the slope of a line that's parallel to the one above? Well, since parallel lines have equal slopes, that one will have an undefined slope too.
As for perpendicular lines, they have slopes that are negative reciprocals of each other. We got that the slope is -2/0. The negative reciprocal of that is 0/2, which simplifies to 0.
Alternatively, you could look at it this way: a horizontal line (a line with zero slope) is perpendicular to a vertical line. So the slope of that line is m = 0.
\(\rule{350}{1}\)
How do you solve formulas and literal equations for a variable?
Answers
Answer:
Move the variables to one side and the constants to the other through subtraction/additions to BOTH SIDES. Then, divide/multiply to get x = some constant.
Step-by-step explanation:
Try Khan Academy.
The world's fastest man, Usain Bolt,
sprinted an amazing 62. 64 meters in 6
seconds. At this rate, how many meters
did Usain Bolt travel in 4 seconds? 1
Answers
Answer:
Step-by-step explanation:
First make a ratio,
6:62.64
Now make an equation
6/62.64=4/x
solve for x...
x=41.76
The total number of centimeters a plant grew each week for the past 5 weeks was 13, 6, 10, 5, and 11. Suppose the mean for 6 weeks was 9 centimeters. How many centimeters did the plant grow the sixth week?
Answers
The required plant grew 9 centimeters in the sixth week.
Let x be the number of centimeters the plant grew in the sixth week.
To estimate x, we can use the formula for the mean (average) of a set of numbers:
mean = (sum of numbers) / (number of numbers)
We know the mean for 6 weeks is 9, so we can write:
9 = (13 + 6 + 10 + 5 + 11 + x) / 6
Multiplying both sides by 6, we get:
54 = 45 + x
Subtracting 45 from both sides, we get:
x = 9
Therefore, the plant grew 9 centimeters in the sixth week.
Learn more about mean here:
https://brainly.com/question/31101410
#SPJ2
charlotte denning earns both $13/hour and $26 for every sale she completes. during the most recent week, she worked 47 hours and made a total of 71 sales.
Answers
Then 26 x 71 = 1846
2457
How elimination method calculator?
Answers
The elimination method is a method for solving systems of linear equations.
The method of elimination consists of removing the same variable from two equations and then finding the value of the other variable that is not eliminated after taking the difference between the two equations.
An equation of the form Ax By = C. Here x and y are variables and A, B and C are constants.
To solve the variables of the given equations by elimination method Let's look at a short comprehensible example.
2x + y = 7 ------> (1)
x + y = 5 -------> (2)
To eliminate 'y', subtract (1) - (2),
2x + y - x - y = 7 - 5
x = 2
Substitute x = 2 in equation(1),
2(2) + y = 7
4 + y = 7
y = 3
Therefore, x = 2, y = 3
know more about elimination method calculator click here;
https://brainly.com/question/30287548
#SPJ4
if factoring (15x -5), and 5 factored from both terms, what remains in the second term, and why ?
Answers
Given:
(15x - 5)
To factor a number from another number means to divide both number.
If 5 is factored from both terms, we have:
15x ÷ 5 = 3x remainder 0
5 ÷ 5 = 1 remainder 0
Therefore, we have:
5(3x - 1)
Thus, the number that remains in the second term is .
This is because when 5 divides 5, the remainder is zero.
5 ÷ 5 = 1 remainder 0
ANSWER:
After factoring we have: 5(3x - 1)
The remainder in the second term is 0
Are the statements true or false?
Select a true or false statement.

Answers
Answer:
It is false and true