y = 2x - 1
y = x² - 2x + 2
Answers
Answer:
x = 1, x = 3 are the solutions
Step-by-step explanation:
Since the left side of both equations is y we can set the right sides equal to each other and solve:
x² - 2x + 2 = 2x - 1
Subtract 2x from both sides:
x² -2x - 2x + 2 = 2x - 2x - 1
x² - 4x + 2 = -1
Add 1 to both sides
x² - 4x + 2 + 1 = -1 + 1
x² - 4x + 3 = 0
We can factor the left side expression as follows:
x² - 4x + 3 = (x - 1)(x -3)
which gives
(x - 1)(x -3) = 0
This means either x - 1 = 0 giving a solution of x = 1
or
x - 3 = 0 giving a solution of x =3
Related Questions
Use the following data to calculate the cost of goods sold for the period: \[ \begin{array}{l} \$ \angle D U, 0 U U . \\ \$ 246,800 \text {. } \\ \$ 242,800 \text {. } \\ \$ 258,800 . \end{array} \]
Answers
The cost of goods sold for the period is $748,400.By accurately calculating the cost of goods sold, businesses can make informed decisions regarding pricing, inventory management, and overall financial performance.
To calculate the cost of goods sold (COGS), we add up the values provided in the data:
COGS = $246,800 + $242,800 + $258,800
= $748,400
The cost of goods sold for the period, based on the given data, is $748,400. The COGS represents the direct costs incurred by a company to produce the goods sold during a specific period. It includes the cost of raw materials, direct labor, and other direct production expenses.
Accurately calculating the COGS is crucial for financial analysis and decision-making. By subtracting the COGS from the total sales revenue, we obtain the gross profit, which is a key indicator of a company's profitability. The COGS also helps determine the company's gross margin, which indicates the percentage of revenue that remains after accounting for the cost of producing goods.
For effective inventory management, it is important for businesses to monitor and control their COGS. It allows them to assess the efficiency of their production processes, identify cost-saving opportunities, and evaluate pricing strategies. Additionally, tracking the COGS helps businesses determine the profitability of specific product lines or services.
The COGS provides valuable insights into a company's operational efficiency and profitability.
To know more about cost , visit;
https://brainly.com/question/19261126
#SPJ11
What is the slope of 3x-2y=7?
Answers
Answer:
The slope is -3/2
Step-by-step explanation:
Hope this helped have a good day!
Sean wants to practice his soccer skills for at least 2.5 hours this week write inequality to represent the number of hours Sean will spend practicing this week. Graph the solution to your inequality from part A on the number line below
Answers
Answer:
x ≥ 2.5
Step-by-step explanation:
Answer:
P > 2.5
Step-by-step explanation:
Question 14 > Suppose f(x) = 3x - 1. Compute each of the following. f(3 + 1) = f(3) + f(1) = f(3-1) = f(3) = f(1) = f(3-1) = f(3) f(1) =
Answers
When computing the given expressions for f(x) = 3x - 1, we find that f(3 + 1) = 15, f(3) + f(1) = 8, f(3-1) = 5, f(3) = 8, f(1) = 2, and f(3-1) = 5.
To find f(3 + 1), we substitute the value of 3 + 1 into the expression for f(x): f(3 + 1) = 3(3 + 1) - 1 = 12 - 1 = 11.
Next, to calculate f(3) + f(1), we substitute the values of 3 and 1 into the expression for f(x) separately and add them together: f(3) + f(1) = (3 * 3 - 1) + (3 * 1 - 1) = 8.
For f(3-1), we substitute the value of 3 - 1 into the expression for f(x): f(3-1) = 3(3-1) - 1 = 5.
Since f(3) and f(1) are both defined as 3x - 1, they have the same value: f(3) = f(1) = 8.
Finally, to compute f(3) f(1), we multiply the values of f(3) and f(1) together: f(3) f(1) = (3 * 3 - 1)(3 * 1 - 1) = 5.
Learn more about computing a given expression:
https://brainly.com/question/15889060
#SPJ11
5. Max wants to start his own lemonade stand. It cost him $3 to make each cup of lemonade plus he has
to pay a $35 renters fee for his stand. He sells the lemonade for $5 per cup.
a. Write a system of linear equations for his cost and his revenue.
Answers
The linear equations for cost price and selling price are c = 3x + 35 and y = 5x.
What is an equation?An equation is a combination of different variables, in which two mathematical expressions are equal to each other.
Let Max make x cups of lemonade cup.
According to given conditions,
Cost of 1 cup of lemonade = $3.
Also, Max pay for renters fee = $35.
The cost of x cups of lemonade = 3x
The total cost c = 3x + 35
Since, Max sells lemonade for $5 per cup.
Let the selling price is represented by y,
Then selling price y = 5x
Hence, linear equations for cost price and selling price are c = 3x + 35 and y = 5x.
To know more about Equation on:
https://brainly.com/question/187506
#SPJ1
HELLPPP DUE TODAY AT 4





Answers
Answer:
2 and 2/3 for the first question
-1/8 for the second one
-1/5 for the third one
ive never done this type of question or maybe it was too long ago for me to remember but out of this answer choices i would guess that its the last one
this is 3
Step-by-step explanation:
you add the numerators which is the top number in order to get 2 and 2/3rds
you subtract 5 from 4 to get -1/8
same situation as the last one, subtract 15 from 11 to make it a negative 4/20 and then simplify that by dividing it by four to get 1/5th
this one i dont understand or remember how to do very well but if i had to guess its the last answer choice
this one you add 3/4 plus 1/4 in order to get 4/4 or rather 1, so basically its asking what 1+1+1 is which is 3
Show the family of conics with the same focus
x^2/a^2+C + y^2/b^2+C = 1
is its own orthogonal family of curves.
Answers
The original equation and the orthogonal equation are the same, we can conclude that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves.
To show that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves, we need to take the derivative of the equation and set it equal to -1/b^2, the slope of the orthogonal line.
First, we take the derivative of the equation with respect to x:
2x/a^2 = -2y/b^2 * dy/dx
Simplifying, we get:
dy/dx = -b^2*x/a^2*y
Now, we set this equal to -1/b^2:
-b^2*x/a^2*y = -1/b^2
Cross-multiplying and simplifying, we get:
x/a^2*y = 1/b^2
Finally, we can rearrange this equation to get:
y = b^2*x/a^2
This equation represents the orthogonal family of curves to the original family of conics. Since the original equation and the orthogonal equation are the same, we can conclude that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves.
Learn about Conics
brainly.com/question/29767685
#SPJ11
Which unit rate is equivalent to 14 miles per gallon? 2 galions 32 miles 32 miles 2 gallons 3 gallons 42 miles 42 miles 3 gallons
Answers
Answer:
32 miles 2 gallons
Step-by-step explanation:
use the chain rule to find dz/dt. z = x2 + y2 + xy, x = sin(t), y = 4et
Answers
The derivative dz/dt can be found using the chain rule. By differentiating each term with respect to t and applying the chain rule, we can calculate dz/dt as follows:
\(dz/dt = 2sin(t)cos(t) + 4e^tcos(t) + 4e^tsin(t) + 4e^t + 4sin(t)e^t.\)
How can we use the chain rule to find the derivative of z with respect to t ?By applying the chain rule, we can find dz/dt as follows: differentiate z with respect to x, then multiply it by dx/dt, and finally differentiate z with respect to y and multiply it by dy/dt.
The function z = x² + y² + xy can be rewritten as z = (sin(t))² + (4e^t)² + (sin(t))\((4e^t)\).
To find dz/dt, we need to find the partial derivatives of z with respect to x and y and multiply them by dx/dt and dy/dt, respectively.
The partial derivative of z with respect to x is (2x + y), and the partial derivative of z with respect to y is (2y + x).
Next, we differentiate x = sin(t) with respect to t, giving us dx/dt = cos(t).
Similarly, differentiating\(y = 4e^t\) with respect to t yields \(dy/dt = 4e^t.\)
Now we can apply the chain rule:
dz/dt = (2x + y) * dx/dt + (2y + x) * dy/dt
Substituting the expressions for x, y, dx/dt, and dy/dt:
\(dz/dt = (2sin(t) + 4e^t) * cos(t) + (2(4e^t) + sin(t)) * (4e^t)\)
Simplifying this expression will yield the final result.
Learn more about chain rule
brainly.com/question/24898810
#SPJ11
suppose that a certain population obeys the logistic equation dy/dt=ry[1−(y/K)].(a) If y0=K/3,find the timeτat which the initial population has doubled. Find the value of τ corresponding tor=0.025 per year.(b) If y0/K=α, find the time T at which y(T)/K=β, where 0<α,β<1. Observe that T→[infinity] as α→0 or as β→1. Find the value of T for r=0.025 per year,α=0.1, andβ=0.9.
Answers
The initial population will double in about 27.73 years.
The population will reach β*K after about 25.44 years.
What is logistic regression?
The logistic model in statistics is a statistical model that depicts the likelihood that an event will occur by making the event's log-odds a linear combination of one or more independent variables. In regression analysis, logistic regression is used to estimate a logistic model's parameters.
The logistic equation is given by:
dy/dt = ry(1 - y/K)
(a) If y0=K/3, we want to find the time t at which the initial population has doubled.
Let Y denote the population size, so we want to find the value of t such that Y(t) = 2*K.
To solve for t, we need to first solve the differential equation using separation of variables:
dy/[y(1 - y/K)] = r*dt
Integrating both sides, we get:
ln|y/K - 1| - ln|y| = r*t + C
where C is a constant of integration. Solving for y, we get:
y(t) =\(K / [1 + Ae^{(-rt)}]\)
where A is a constant determined by the initial condition y(0) = K/3. Substituting this initial condition, we get:
K/3 = K / [1 + A]
Solving for A, we get:
A = 2
Substituting this value of A, we get:
y(t) = \(K / [1 + 2e^'(-rt)}]\)
Now, we need to find the time t such that Y(τ) = 2*K. Substituting Y(t) = y(t)*K, we get:
Y(t) =\(K^2 / [1 + 2e^{(-rt)}]\)
So we need to solve the equation:
2K = \(K^2 / [1 + 2e^{(-rt)}]\)
Solving for t, we get:
t = (1/r) * ln(2)
Substituting r = 0.025 per year, we get:
t = (1/0.025) * ln(2) ≈ 27.73 years
Therefore, the initial population will double in about 27.73 years.
(b) If y0/K=α, we want to find the time T at which y(T)/K=β. Letting Y denote the population size, we want to find the value of T such that Y(T) = β*K.
Following a similar procedure as in part (a), we can solve the logistic equation and obtain:
y(t) = \(K * [α/(α + (1 - α)*e^{(-rt)})]\)
Substituting Y(t) = y(t)*K, we get:
Y(t) = K *\([α/(α + (1 - α)e^{(-rt)})] = \beta K\)
Solving for t, we get:
t = (1/r) * ln[(β/α) - 1] - (1/r) * ln[(1 - α)/α]
Substituting r = 0.025 per year, α = 0.1, and β = 0.9, we get:
t = (1/0.025) * ln[8] - (1/0.025) * ln[9] ≈ 25.44 years
Therefore, the population will reach β*K after about 25.44 years.
The initial population will double in about 27.73 years.
The population will reach β*K after about 25.44 years.
We are given a sample of Logistic regression. Please refer the following link
https://brainly.com/question/28391630
#SPJ1
5 million and 300 in standard form
Answers
If there are 10 terms of the sequence {2, 7, 12, 17, ...}, what is its mean?
Answers
Answer:
24.5
Step-by-step explanation:
The mean is calculated as
mean = \(\frac{sum}{count}\)
The consecutive terms in the sequence have a common difference d
d = 7 - 2 = 12 - 7 = 17 - 12 = 5
This indicates the sequence is arithmetic with sum to n terms
\(S_{n}\) = \(\frac{n}{2}\) [ 2a₁ + (n - 1)d ]
where a₁ is the first term and d the common difference
Here a₁ = 2 and d = 5 , thus
\(S_{10}\) = \(\frac{10}{2}\) [ (2 × 2) + (9 × 5) ]
= 5(4 + 45)
= 5 × 49 = 245 , then
mean = \(\frac{245}{10}\) = 24.5
Solutions to EquationsDetermine which of the following are true statements. Check all that applyOw=13 is a solution to ( – 5w – 6) – ( – 4w + 7) = 14Oc= – 3 is a solution to -C – 3 = – 2c – 6x = 12 is a solution to 4(62 + 7) = 2(5z + 98)Oy = – 5 is a solution to 3y + 2 = 4y + 7

Answers
You have the following expression:
\(\frac{1-3z}{8}=\frac{10-2z}{10}\)In order to determine if z=-5 is a solution to the previous equation, replace z=-5 and verify the equation, just as follow:
\(\begin{gathered} \frac{1-3(-5)}{8}=\frac{10-2(-5)}{10} \\ \frac{16}{8}=\frac{20}{10} \\ 2=2 \end{gathered}\)Hence, z=-5 is a solution of the given equation
A- 105.6 cm2
B- 43.76 cm2
C- 452.16 cm2

Answers
Answer:
C. 452.16 cm2
Step-by-step explanation:
A= π r^2 = π · 12^2 ≈ 452.38934 or 452.38
The closest answer to that listed is C
formula:(A = π r²)
π = 3.14
r(radius)^2= radius to the second power.
Please help if you wantbbrainleist! :(

Answers
hillary and 23 of her friends went on a hayride. there are 8 more boys then girls on the ride.how many boys and girls were on the ride
Answers
Answer:
16 boys total
8 girls total
Step-by-step explanation:
We know that Hillary invited 23 of her friends, including her, this lets us know there are 24 people total.
Given, we already know 8 of that 24 are boys, which leaves us with 16 people left.
24 - 8 = 16
We simply know there are 8 girls and 8 boys from this problem and on top we add 8 more boys because there are 8 more boys.
_______________________________
Total = 1 + 23 = 24
Girls:
x + (x + 8) = 24
2x = 16
x = 8
Boys:
x + 8 = 1b
3/13 as a decimal rounded to the nearest thousandth
Answers
Answer:
0.231
Step-by-step explanation:
Answer:
3/13 round to the nearest thousandth is 0.231
Step-by-step explanation:
ab
For the given values, perform the indicated operations for
c
and express the answer in scientific notation and standard
form.
a = = 76.1
b= 818,000.000
C
= 0.000016
Answers
Now
\(\\ \sf\longmapsto abc=76.1\times 818000\times 0.000016\)
\(\\ \sf\longmapsto abc=995.9968\)
PLEASE HELPPPPPPPPP!!!!!!!!

Answers
Jim can make 2 cupcakes (the y value) with one cup of flour (the x value). How many cupcakes can he make with
5 cups of flour?
Answers
X 3.1.PS-11
Question Help
Challenge An arts academy requires there to be 3 teachers for every 72 students and 4 tutors for
every 44 students. How many students does the academy have per teacher? Per tutor? How many
tutors does the academy need if it has 77 students?
Answers
Answer:
a) 24 students per teacher
b) 7 tutors for 77 students
Step-by-step explanation:
72/3 = 24
4/44*77= 7
.Damian wrote the number five and thirty-eight thousandths as 5.38. Was he correct or not? if so, what was the error
Answers
Answer:
he is incorrect.
Step-by-step explanation:
It would be 5 and 38 HUNDRETHS because the first number after the decimal is the tenths.
Can someone answer both of these questions?
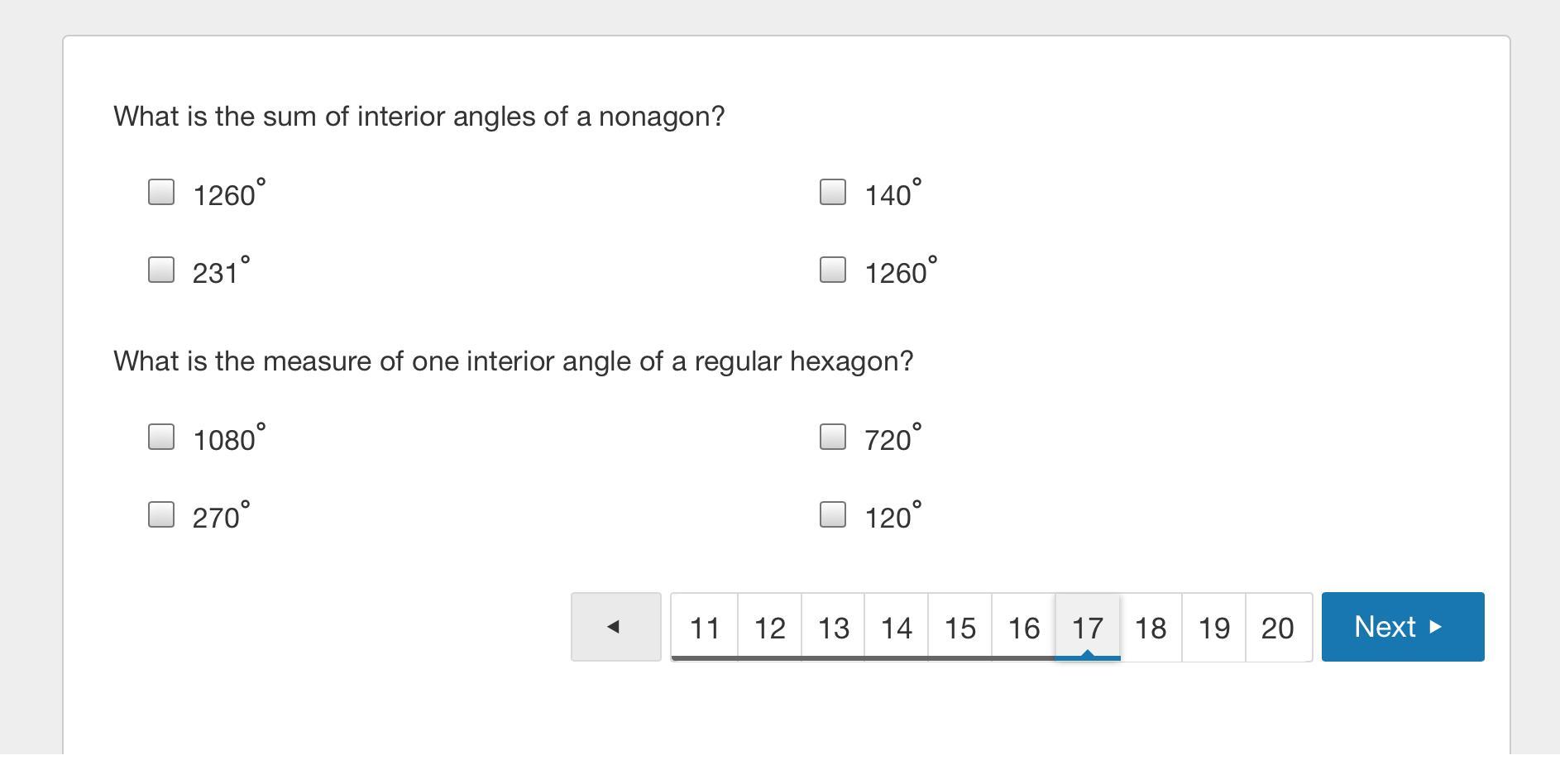
Answers
Answer:
First one is 1260°
Second one is 720°
Step-by-step explanation:
Hope this helped :)
Suppose you have an algorithm A that takes as input an array M[0,1,...,n - 1] of n integers. The algorithm is defined by two functionsf: Z → Zand g: ZXZ â€" Z. If n = 1, then the algorithm computes a function f (g), where is the single entry in the array, and returns this integer value. For larger values of n, the algorithm Computes two new arrays that start at positions i = 0 and [n/3 - 1] and that include [2n/3] elements. Thus, if n = 15, the new arrays would begin at positions 0 and 4 and contain 10 elements each The algorithm then runs recursively on each subarray, and stores the value. This returns an ordered set of two integers, x, y,. The algorithm then computes g(x, y), and returns this value. We would like to write down a function (n) for the running time of this algorithm on inputs of arrays of n elements. Assume that computing f (9) and g(x, y) each cost only one operation. Counting all the operations for each step, which of the following recurrence relations would seem to fit? To make the problem easy to solve, you should assume that n = 3k for some non-negative integer a. t(1) = and t(n) = 2t(n/2) + 1, for some positive constant C O b. t(1) = C, and t(n) = 21(2n/3), for some positive constant c. 1(1) = C, and t(n) = 2t(2n/3) + C2, for some positive constants C, C2 d. 1(1) = C, and t(n) = 21(2n/3) + C2n, for some positive constants C, C2 e. f(1) = C, and t(n) = 2t(n/3) + C2, for some positive constants C, C2
Answers
Based on the given algorithm, we can analyze the recurrence relation for the running time of the algorithm on inputs of arrays of n elements.
Let's denote the running time of the algorithm for an input of size n as t(n).
For n = 1, the algorithm computes f(g) for a single entry in the array, which costs a constant time, let's say C1. Therefore, we have:
t (1) = C1
For larger values of n, the algorithm splits the array into two subarrays of size 2n/3 each and runs recursively on each subarray. This step incurs a running time of t(2n/3) for each subarray.
Additionally, the algorithm performs the computation g(x, y) on the resulting ordered set of two integers, which costs a constant time, let's say C2.
Considering these factors, we can write the recurrence relation for the running time as:
t(n) = 2t(2n/3) + C2
Therefore, the correct option among the given recurrence relations that seems to fit the running time of the algorithm is:
c. t(1) = C, and t(n) = 2t(2n/3) + C2, for some positive constants C, C2
Learn more about recurrence relation here:
brainly.com/question/27381972
#SPJ11
Law of sines: startfraction sine (uppercase a) over a endfraction = startfraction sine (uppercase b) over b endfraction = startfraction sine (uppercase c) over c endfraction 2.2 units 2.4 units 3.0 units 3.3 units
Answers
The possible approximate lengths of b are: 2.3 units and 7.8 units
We know that the law of sines for triangle is:
The ratios of the length of all sides of a triangle to the sine of the respective opposite angles are in proportion.
This means, for triangle ABC,
\(\frac{sin~ A}{a} =\frac{sin~B}{b} =\frac{sin~ C}{c}\)
where a is the length of side BC,
b is the length of side AC,
c is the length of side AB.
For triangle ABC consider an equation from sine law,
\(\frac{sin~ A}{a} =\frac{sin~ C}{c}\)
here, c = 5.4, a = 3.3, and m∠A = 20°
\(\frac{sin~ 20}{3.3} =\frac{sin~ C}{5.4}\\\\\frac{0.3420}{3.3} =\frac{sin~ C}{5.4}\)
0.3420 × 5.4 = 3.3 × sin(C)
sin(C) = 0.5596
∠C = arcsin(0.5596)
∠C = 34.03° OR 145.9°
∠C ≈ 34° OR 146°
We know that the sum of all angles of triangle is 180 degrees.
so, ∠A + ∠B + ∠C = 180°
when m∠C = 34°,
20° + ∠B + 34.03° = 180°
∠B = 125.97°
m∠B = 126°
when m∠C = 146°,
20° + ∠B + 146° = 180°
m∠B = 14°
Now consider equation,
\(\frac{sin~ A}{a} =\frac{sin~ B}{b}\\\\\frac{sin~20^{\circ}}{3.3} =\frac{sin~ 126^{\circ}}{b}\)
b × 0.3420 = 0.8090 × 3.3
b = 7.8 units
when m∠B = 14°,
\(\frac{sin~20^{\circ}}{3.3} =\frac{sin~ 14^{\circ}}{b}\)
b × 0.3420 = 0.2419 × 3.3
b = 2.3 units
Learn more about the law of sines here:
https://brainly.com/question/17289163
#SPJ4
The complete question is:
Law of sines: StartFraction sine (uppercase A) Over a EndFraction = StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction
In ΔABC, c = 5.4, a = 3.3, and measure of angle A = 20 degrees. What are the possible approximate lengths of b? Use the law of sines to find the answer.
2.0 units and 4.6 units
2.1 units and 8.7 units
2.3 units and 7.8 units
2.6 units and 6.6 units
Using the definition of martingales
Let two martingales in respect to the same filtration. Prove that the process is a supermartingale.
Answers
In a supermartingale , the current variable (\(X_{t}\)) is an overestimate for the upcoming \(X_{t + 1}\).
A sequence of random variable (\(X_{t}\)) adapted to a filtration (\(F_{t}\)) is a martingale (with respect to (\(F_{t}\))) if all the following holds for all t :
(i) E|\(X_{t\)| < ∞
(ii) E[ \(X_{t + 1}\)|\(F_{t}\)] = \(X_{t}\)
If instead of condition (ii) we have E [\(X_{t + 1}\)|\(F_{t}\)] ≥ \(X_{t}\) for all t , we then say that (\(X_{t}\)) is submartingale with respect to (\(F_{t}\)).
If instead of condition (ii) we have E [ \(X_{t + 1}\) | \(F_{t}\)] ≤\(X_{t}\) for all t , we then say that (\(X_{t}\)) is supermartingale with respect to (\(F_{t}\)).
Learn more about Martingale :
https://brainly.com/question/32615326
#SPJ11
Use the law of cosines to solve for x. (Add proofs) Helpppp

Answers
The value of x in the triangle is 32
How to find xThe angles are found using the dimensions,
The angles are found first using cosine rule by the formula
c = √(a² + b² - 2 cos C)
Using the values in the problem
c = √(25² + 20² - 2 cos 108)
c = √(25² + 20² - 2 cos 108)
c = √(1025 + 0.6180)
c = √(1025.6180)
c = 32
Learn more about cosine and sine rule at
https://brainly.com/question/29247917
#SPJ1
HELP FAST! In triangle ABC, the right angle is at vertex C, a = 714 cm and the measure of angle A is 78° . To the nearest cm, what is the length of side c?
Answers
Answer:
sine (78°) = 714 / side c
side c = 714 / sine (78°)
side c = 714 / 0.97815
side c = 729.95
Step-by-step explanation:

which of the following series satisfy the given condition. the series is geometric with x = 1/3.
Answers
The answer is Series 1. It satisfies the given condition as it is a geometric series with a common ratio of 1/3. Each term in this series is obtained by multiplying the previous term by 1/3, which confirms that it is indeed a geometric series with the given condition.
We need to test each series to see if it is geometric with x = 1/3. Remember, a geometric series is one in which each term is obtained by multiplying the previous term by a constant value. In this case, that constant value is x = 1/3. Let's test three series to see if they fit the given condition: 1) 3, 1, 1/3, 1/9, 1/27, ...
To see if this series is geometric with x = 1/3, we can check if each term is obtained by multiplying the previous term by 1/3.
1/3 ÷ 1 = 1/3
1/9 ÷ 1/3 = 1/3
1/27 ÷ 1/9 = 1/3
Since each term is obtained by multiplying the previous term by 1/3, this series is geometric with x = 1/3.
2) 1, 1/3, 3, 1/9, 9, ...
To test if this series is geometric with x = 1/3, we can check if each term is obtained by multiplying the previous term by 1/3.
1/3 ÷ 1 = 1/3
3 ÷ 1/3 = 9
1/9 ÷ 3 = 1/27
Since the terms are not consistently obtained by multiplying the previous term by 1/3, this series is not geometric with x = 1/3.
3) 1, 1/3, 1/9, 1/27, ...
To test if this series is geometric with x = 1/3, we can check if each term is obtained by multiplying the previous term by 1/3.
1/3 ÷ 1 = 1/3
1/9 ÷ 1/3 = 1/3
1/27 ÷ 1/9 = 1/3
Since each term is obtained by multiplying the previous term by 1/3, this series is geometric with x = 1/3.
To know more about geometric visit :-
https://brainly.com/question/12500691
#SPJ11
What is the Riemann Hypothesis?