Answers
y intercept- 2.5
Related Questions
What are the dimensions of the rectangle shown on the coordinate plane?
The base is 5 units and the height is 3 units.
The base is 4 units and the height is 7 units.
The base is 7 units and the height is 5 units.
The base is 7 units and the height is 3 units.

Answers
Does the data for Amit’s puppy show a function? Why or why not?




Answers
Answer:
no its not a function
Step-by-step explanation:
because the lines on the graph are not equal\in a straight line(the puppy is not gaining the same amount each week)
Describe what a number line representing d>−4 would look like. (1 point)
Responses
hollow circle at −4, with an arrow extending to the right
hollow circle at , negative 4, , with an arrow extending to the right
solid circle at −4, with an arrow extending to the right
solid circle at , negative 4, , with an arrow extending to the right
solid circle at −4, with an arrow extending to the left
solid circle at , negative 4, , with an arrow extending to the left
hollow circle at −4, with an arrow extending to the left
, hollow circle at , negative 4, , with an arrow extending to the left
Answers
A number line representing d>−4 would be a straight line with a solid or hollow circle at the point −4, depending on whether or not −4 is included in the solution.
If the inequality is d>−4, this means that any value of d that is greater than −4 can satisfy the inequality. For example, d=−3 or d=0 would satisfy the inequality, but d=−5 would not.
The arrow extending to the right from the circle indicates that the number line continues in the positive direction, indicating that any value of d greater than −4 is a solution. This depiction is straightforward and easy to understand, providing a visual representation of the possible solutions for the inequality.
In algebraic terms, the number line representation of an inequality can help students better understand the concept of absolute value and the importance of understanding the direction of the inequality when solving problems. It can also be useful in practical applications, such as interpreting temperature ranges or measuring distances. Overall, a number line helps visualize the concept of d>−4 by depicting all possible values of d that satisfy the inequality.
To know more about number line click here:
brainly.com/question/13189025
#SPJ4
Raul sells fancy new TVs. They cost $600. He sells the TV for $900. What is his percent markup? show your work
Answers
Answer:
His percent markup is 150%
Step-by-step explanation:
If an object is an irregularly shaped solid and it is dropped into a graduated cylinder and it displaces 25 mL of water and has a mass of 50 grams what is the density of this irregular shaped object?
Answers
Answer:
25mL
Step-by-step explanation:
Density of this irregular shaped object is 2gm/cm³
Given that;Amount of water displayed = 25 ml
Mass of solid = 50 grams
Find:Density of this irregular shaped object
Computation:1 ml = 1 cubic centimeter
So,
Density of this irregular shaped object = Mass of object / Volume of object
Density of this irregular shaped object = 50 / 25
Density of this irregular shaped object = 2gm/cm³
Learn more:https://brainly.com/question/25571066?referrer=searchResults
What is the difference between minimum and infimum?
Answers
The terms minimum and infimum are both related to the concept of lower bounds in mathematics. A minimum is the smallest value in a set of numbers, whereas an infimum is the greatest lower bound of a set.
A minimum is a value that is less than or equal to all other values in the set, while an infimum is a value that is less than or equal to all other values in the set, but not necessarily the smallest value.
For example, if we consider the set {2, 4, 6}, the minimum is 2 and the infimum is also 2. However, if we consider the set {2, 4, 6, 8}, the minimum is 2 and the infimum is 4. In the latter set, 4 is the greatest lower bound, meaning that all other values in the set are greater than or equal to 4.
know more about mathematics here
https://brainly.com/question/15209879#
#SPJ11
What is the domain? I need help on this problem

Answers
The domain of the function \(f(x) = \sqrt{\frac{1}{3}x + 2\) is (d) x ≥ -6
How to determine the domain of the functionFrom the question, we have the following parameters that can be used in our computation:
\(f(x) = \sqrt{\frac{1}{3}x + 2\)
Set the radicand greater than or equal to 0
So, we have
1/3x + 2 ≥ 0
Next, we have
1/3x ≥ -2
So, we have
x ≥ -6
Hence, the domain of the function is (d) x ≥ -6
Read more about domain at
https://brainly.com/question/31900115
#SPJ1
Determine the intercepts of the line.

Answers
Answer:
y=(0,-45)
x=(-10,0)
Step-by-step explanation:
Find the probability of exactly threesuccesses in six trials of a binomialexperiment in which the probability ofsuccess is 50%.Round to the nearest tenth of apercent.[ ? ]%

Answers
We need to find the probability of exactly three successes in six trials of a binomial experiment. Probability of success 50% (no success is 50%).
To find this probability, we need to use the following formula for Bernoulli Trials (or Binomial Experiment):
\(comb\text{(6, 3) }\cdot(\frac{1}{2})^3\cdot(\frac{1}{2})^{(6-3)}\)The combinations are given by:
\(\frac{6!}{(6-3)!\cdot3!}=\frac{6\cdot4\cdot3!}{3!\cdot3!}=\frac{6\cdot4}{3\cdot2\cdot1}=\frac{24}{6}=4\)Then, we have:
\(4\cdot(\frac{1}{2})^3\cdot(\frac{1}{2})^3=0.0625\)Thus, the probability of exactly three successes in six trials of a binomial experiment (which the probability of success is 50%) is 0.0625.
Rounding to the nearest tenth is about p = 0.1 (1/10) or 10%.
Which system of equations has a solution of approximately (0.7, –1.4)?
Answers
Answer:
Step-by-step explanation:
Given question is incomplete; here is the complete question,
"Which system of equations has a solution of approximately (0.7, -1.4)?"
A). x - y = 2 and x + 2y = -2
B). x - 2y = -2 and x + y = 2
C). x - y = 2 and x - 2y = -2
D). x + y = 2 and x + 2y = -2
"If the given point (0.7, -1.4) is the solution of the system of equations, it will satisfy both the equations"
To check whether the statement given above is true or false we will substitute the values of x and y in the given equations,
A). x - y = 2
0.7 - (-1.4) = 2.1
≈ 2
x + 2y = -2
0.7 + 2(-1.4) = -2.1
≈ -2
True.
B). x - 2y = -2
0.7 - 2(-1.4) = 3.5
x + y = 2
0.7 - 1.4 = -0.7
False.
C). x - y = 2
0.7 - (-1.4) = 2.1 ≈ 2
x - 2y = -2
0.7 - 2(-1.4) = 3.5
False.
D). x + y = 2
0.7 - 1.4 = -0.7
x + 2y = -2
0.7 + 2(1.4) = 3.5
False.
if we compute a 95onfidence interval 12.65 ≤ μ ≤ 25.65 , then we can conclude that.
Answers
Based on the computed 95% confidence interval, we can conclude that we are 95% confident that the true population mean falls within the range of 12.65 to 25.65.
A confidence interval is a range of values that provides an estimate of the true population parameter. In this case, we are interested in estimating the population mean (μ). The 95% confidence interval, as mentioned, is given as 12.65 ≤ μ ≤ 25.65.
Interpreting this confidence interval, we can say that if we were to repeat the sampling process many times and construct 95% confidence intervals from each sample, approximately 95% of those intervals would contain the true population mean.
The confidence level chosen, 95%, represents the probability that the interval captures the true population mean. It is a measure of the confidence or certainty we have in the estimation. However, it does not guarantee that a specific interval from a particular sample contains the true population mean.
Therefore, based on the computed 95% confidence interval, we can conclude that we are 95% confident that the true population mean falls within the range of 12.65 to 25.65.
Learn more about confidence interval here:
https://brainly.com/question/13067956
#SPJ11
What is 36 ÷ ( 1 - |2-7| )?
Answers
Answer:
36 / (1 - |2 - 7|) = -9
Step-by-step explanation:
Answer:
-9
Step-by-step explanation:
Given the figure, find the values of x and z.

Answers
\(\\ \sf\longmapsto 8x-38=90\)
\(\\ \sf\longmapsto 8x=90+38\)
\(\\ \sf\longmapsto 8x=128\)
\(\\ \sf\longmapsto x=16\)
Now
\(\\ \sf\longmapsto z+90=180\)
\(\\ \sf\longmapsto z=90\)
Samir is going to invest $22,000 and leave it in an account for 9 years. Assuming the interest is compounded monthly, what interest rate, to the nearest tenth of a percent, would be required in order for Samir to end up with $38,000?
Answers
The interest rate required to get a total amount of $38,000.00 from compound interest on a principal of $22,000.00 compounded 1 times per year over 9 years is 9.0909 % per year.
What is the interest rate?The amount a lender charges a borrower is called an interest rate, and it is expressed as a percentage of the principal, or the loaned amount. Typically, a loan's interest rate is expressed as an annual percentage rate, or APR .
r = n[(A/P)1/nt - 1]
r = 1 × [(38,000.00/22,000.00)1/(1)(9) - 1]
r = 0.0909090
Then convert r to R as a percentage
R = r × 100
R = 0.0909090 × 100
R = 9.0909 %/year
The interest rate required to get a total amount of $38,000.00 from compound interest on a principal of $22,000.00 compounded 1 times per year over 9 years is 9.0909 % per year.
To learn more about compound interest here:
brainly.com/question/24274034
#SPJ1
Answer: 6.1
Step-by-step explanation:
help me with this please

Answers
The values of a, b, c are 152°, 28°, 152° respectively.
What are angle at a point?Angles around a point describes the sum of angles that can be arranged together so that they form a full turn.
The sum of angles at a point will give 360°.
This means that a + b + c + 28 = 360
c +28 = 180° ( angle on a straight line)
c = 180 -28
c = 152°
c = a( alternate angles are equal)
therefore the value of a = 152°
b = 28( alternate angles are equal)
therefore the value of b is 28
therefore the values of a, b, c are 152°, 28°, 152° respectively
learn more about angle at a point from
https://brainly.com/question/25716982
#SPJ1
Using suitable identity, find the value of 87^3+ 13^3/
87^2 −87 ×13 + 13^2
Answers
The value of the given expression [\(87^3+ 13^3/87^2 -87 * 13 + 13^2\)] by simplifying the numerator and denominator using suitable identities is 100.
We will first calculate the numerator:
As (\(a^3\) + \(b^3\)) = (a + b)(\(a^2\) - ab + \(b^2\)) :
\(87^3\) + \(13^3\) = (87 + 13)(\(87^2\) - \(87 * 13\) + \(13^2\))
= 100(\(87^2\) - 87 * 13 + \(13^2\))
Now, calculate the denominator:
\(87^2 - 87 * 13 + 13^2\)
As,(\(a^2 -2ab +b^2\)) =\((a - b)^2\):
\(87^2 - 87 * 13 + 13^2 = (87 - 13)^2\)
\(= 74^2\)
So by solving the equation further:
\((87^3+13^3) / (87^2- 87 * 13+13^2) = 100*(87^2- 87 *13 + 13^2)/(87^2 - 87 * 13 + 13^2)\)
As we can see the numerator and denominator are the same expressions (\(87^2 - 87 * 13 + 13^2\)). so, they cancel each other:
\((87^3 + 13^3) / (87^2 - 87 * 13 + 13^2) = 100\)
So, the value of the given expression is 100.
To know more about the expression:-
https://brainly.com/question/14083225
Sixty-four percent of voters in a very large electorate support candidate Smith in an upcoming election. A student employee working the evening shift at a telephone survey facility calls voters at random and asks them which candidate they prefer. a. What is the probability that, among five voters the student calls, exactly one supports candidate Smith? b. What is the probability that, among five voters the student calls, at least one supports candidate Smith? c. What is the probability that the first voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach the first voter who supports candidate Smith? d. What is the probability that the third voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach three voters who supports candidate Smith?
Answers
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4
\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5
\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls. The calculation results in approximately 0.369, or 36.9%.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
[P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
[P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
Find the value of x in each triangle

Answers
Answer:
Step-by-step explanation:
The sum of a triangle’s angles is always 180 degrees so
x+x+25=180
2x+25=180
2x=155
x=77.5 degrees
Multiply the monomials:
(3/4)pq, (1/2)qr^2, -5q^2r^3 and -6r^5
Answers
Given monomials are (3/4)pq , (1/2)qr² , -5p²r³ and -6r⁵
On multiplying them then
⇛ [(3/4)pq]×[(1/2)qr²]×[-5p²r³]×[-6r⁵]
⇛ [(3/4)×(1/2)×(-5)×(-6)]×(pq×qr²×p²r³×r⁵)
⇛[(3×1×-5×-6)/(4×2)](p×p²)×(q×q)×(r²×r³×r⁵)
⇛ (90/8)×p³×q²×r¹⁰
Since a^m × a^n = a^(m+n)
⇛ (45/2)×p³×q²×r¹⁰
⇛( 45/2 ) p³q²r¹⁰
Answer:- [(3/4)pq]×[(1/2)qr²]×[-5p²r³]×[-6r⁵] = (45/2)p³q²r¹⁰
Find I need answers for 2 questions
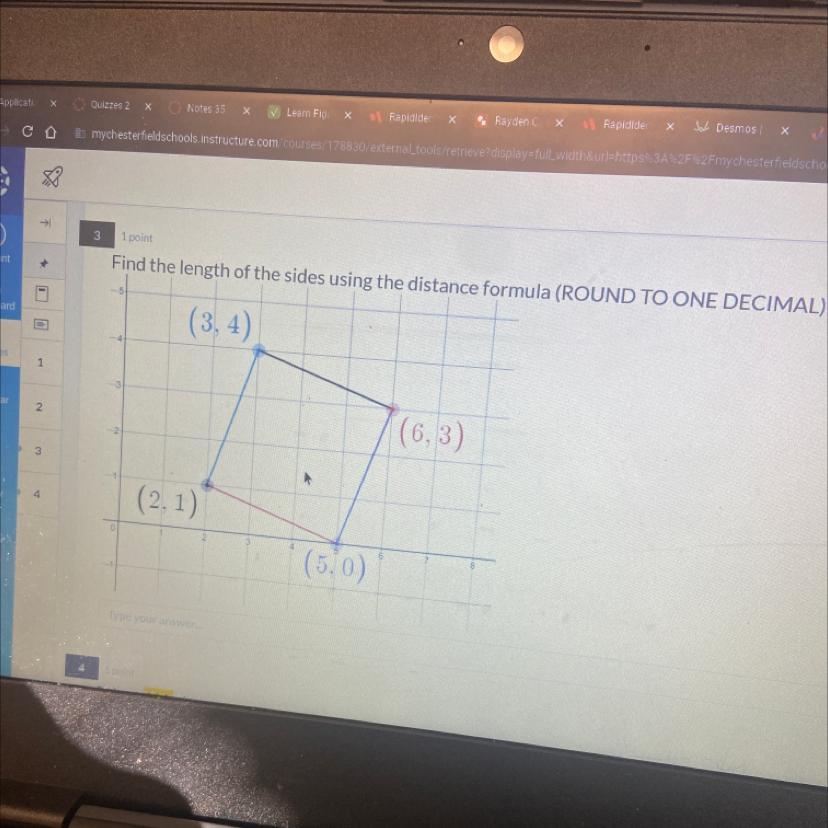
Answers
Answer:
12.8Step-by-step explanation:
A^2+B^2=C^2
A= x2-x1
B=y2-y1
(3,4) and (6,3)
6-3= 3
3-4=-1
3^2=9
-1^2=1
9+1=10
9+1=C^2
10=C^2
\(\sqrt{10}\)=3.16227766
Round up= 3.2
We can tell that this image is, a square, so 3.2*4 sides to get 12.8.
12.8 is the length of all of the sides combined.
How do you solve a differential equation with exponential equations?
Answers
To solve a differential equation with exponential equations, start by isolating the dependent variable and any coefficients that may exist on either side of the equation. Next, take the natural logarithm of both sides of the equation and use the properties of logarithms to simplify the equation. Solve for the dependent variable. Finally, take the exponential of both sides of the equation and simplify it to get the solution.
For example, consider the differential equation dy/dx = 2y.
Isolate the dependent variable to get y = dx/2.
Then, take the natural logarithm of both sides to get ln(y) = ln(dx/2).
Use the property ln(a/b) = ln(a) - ln(b) to get ln(y) = ln(dx) - ln(2).
Solve for ln(y) to get ln(y) = ln(dx) - ln(2).
Then, take the exponential of both sides to get \(y = e^{ln(dx) - ln(2)}\) and simplify to get the solution \(y = (dx/2) e^{ln(dx)}\).
Know more about Logarithm here :
https://brainly.com/question/30976287
#SPJ11
May I please receive help?

Answers
Answer:
Area of shaded region is 160.14m²
Step-by-step explanation:
To find the area of the shaded region, subtract the area of inner circle from the area of outer one
a=πr²
(3.14)7²=153.86
(3.14)10²=314
314-153.86=160.14
let a ball be drawn from an urn containing 4 balls, numbered 1, 2, 3, 4. each ball is equally likely to be drawn. consider the following three events: e
Answers
In all cases, the probabilities are equal to 1/4, indicating that the probability of the intersection of events E, F, and G with any other event is the same.
To calculate the probabilities P(EF), P(EG), and P(FG), we need to determine the intersection of the events E, F, and G and divide it by the total number of possible outcomes, which is 4.
Event E = {1, 2}
Event F = {1, 3}
Event G = {1, 4}
To calculate P(EF), we need to find the intersection of E and F, which is the common element 1. Therefore, P(EF) = 1/4.
To calculate P(EG), we need to find the intersection of E and G, which is also the common element 1. Therefore, P(EG) = 1/4.
To calculate P(FG), we need to find the intersection of F and G, which is the common element 1. Therefore, P(FG) = 1/4.
In all cases, the probabilities are equal to 1/4, indicating that the probability of the intersection of events E, F, and G with any other event is the same.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Let a ball be drawn from an urn containing four balls, numbered 1,2, 3, 4. Let E={1,2}, F={1,3}, and G={1,4}. If all four outcomes are assumed equally likely, then what is P(EF), P(EG), and P(FG)?
27) An amusement park ride, the Demon Drop, includes a drop of close to 100 feet. Use the given equation to
approximate the time (seconds) that it takes the dropped object to fall a distance of about feet. Solve for "t" to
the nearest tenth.

Answers
The square root of 100/16 is 2.5. It is already rounded to the nearest tenth. Use a calculator.
\(\sqrt{25} is an irrational
Answers
Answer:
Is Square Root of 25 Rational or Irrational?
Step-by-step explanation:
A rational number can be expressed in the form of p/q. Because √25 = 5 and 5 can be written in the form of a fraction 5/1. It proves that √25 is rational.
The answer is:
⇨ √25 is a rational numberWork/explanation:
What are rational numbers?
Rational numbers are integers and fractions.
Irrational numbers are numbers that cannot be expressed as fractions, such as π.
Now, \(\bf{\sqrt{25}}\) can be simplified to 5 or -5; both of which are rational numbers.
Hence, √25 is rational.Plz I really need help and thank youuu

Answers
Because pH affects the reaction, a student carefully creates a suitable aqueous solvent for the reaction. After bubbling CO2 through the solution, he checks the pH and is surprised to find that it is not the same as the original value. What is the most likely cause for this
Answers
The most likely cause for the change in pH after bubbling CO2 through the solution is the formation of carbonic acid.
When CO2 is bubbled through an aqueous solution, it can react with water to form carbonic acid (H2CO3). This reaction occurs due to the dissolution of CO2 in water, which undergoes a chemical equilibrium process. Carbonic acid is a weak acid that can release hydrogen ions (H+) into the solution, thus lowering the pH. The presence of carbonic acid lowers the pH value compared to the original pH of the solvent.
This phenomenon is commonly observed when CO2 is dissolved in water, such as in carbonated beverages. The carbonic acid formed from the reaction with CO2 contributes to the acidic properties of the solution. Therefore, the most likely cause for the change in pH after bubbling CO2 through the solution is the formation of carbonic acid, leading to a decrease in pH.
Learn more about pH here:
https://brainly.com/question/2288405
#SPJ11
A jeweler makes a pair of earrings by cutting two 50^{\circ} sectors from a silver disk.
a. Find the area of each sector.
Answers
a. The area of each sector is 1.7 cm^2
b. If the weight of the silver disk is 2.3 grams, the silver wedge for each earring weighs approximately 319.4 milligrams.
Answer:
a. To find the area of each sector, we need to use the formula for the area of a sector: A = (θ/360°) * π * r^2, where θ is the central angle of the sector and r is the radius of the disk.
Given that the central angle is 50° and the radius is 2 cm, we can substitute these values into the formula:
A = (50°/360°) * π * (2 cm)^2
Simplifying the calculation:
A = (5/36) * π * 4 cm^2
A ≈ 1.7 cm^2
Therefore, the area of each sector is approximately 1.7 cm^2.
b. To find the weight of the silver wedge for each earring, we need to calculate the weight per unit area.
Given that the weight of the silver disk is 2.3 grams and the area of each sector is 0.694 cm^2, we can use the formula:
Weight per unit area = Total weight / Total area
Substituting the given values:
Weight per unit area = 2.3 grams / (2 * 0.694 cm^2)
Simplifying the calculation:
Weight per unit area ≈ 0.3194 grams/cm^2
To convert grams to milligrams, we can use the conversion factor 1 gram = 1000 milligrams. Therefore, the weight per unit area in milligrams is:
Weight per unit area ≈ 0.3194 grams/cm^2 * 1000 milligrams/gram
Simplifying the calculation:
Weight per unit area ≈ 319.4 milligrams/cm^2
Therefore, the silver wedge for each earring weighs approximately 319.4 milligrams.
Complete Question:
A jeweler makes a pair of earrings by cutting two 50° sectors from a silver disk. radius of the disk is 2 cm
a. Find the area of each sector.
b. If the weight of the silver disk is 2.3 grams, how many milligrams does the silver wedge for each earring weigh?
To know more about sector refer here:
https://brainly.com/question/29055300
#SPJ11
The attendance over a weekly period of time at a movie theater is normally distributed with a mean of 10,000 and a standard deviation of 1000 persons. Find the percent of attendance figures that differs from the mean by 1500 persons or more.
Answers
The percent of attendance figures that differs from the mean by 1500 persons or more is 6.68%.
From the question above, Mean μ = 10,000
Standard Deviation σ = 1,000
The formula for z-score is :
z = (x-μ) / σ
Where, x = observation
z = z-score
Mean μ = 10,000
Standard Deviation σ = 1,000
From the above formula, let's calculate z-score for x = 11,500
z = (x-μ) / σ
z = (11,500 - 10,000) / 1000
z = 1.5
Now, find the probability of attendance figures that differs from the mean by 1500 persons or more.
P(z ≥ 1.5) = 0.0668
To find the percentage, we need to multiply the above value by 100.
P(z ≥ 1.5) × 100 = 0.0668 × 100 = 6.68%
Learn more about the mean at
https://brainly.com/question/31316869
#SPJ11
What is the most picked number between 1 and 10?
Answers
The most picked number between 1 and 10 is statistically 7.
"Most picked number" generally refers to the number that is most frequently chosen or selected.
It is difficult to determine the value in general without any specific context or situation.
However, statistically speaking, the number 7 is often considered the most popular choice. This is because it is considered a lucky number in many cultures and is also a common choice for people who do not have a specific number in mind.
Nevertheless, it's important to note that this may not always be the case and can vary depending on the context or situation as the probability of picking each number is equally likely (0.1).
Learn more about most picked number from the below link:
https://brainly.com/question/30763377
#SPJ4
