Answers
Answer:x=9z + 16
z= x/9 + 16/9
Step-by-step explanation: dont know if i solve for x or z so i did both subtract 16 from both sides for x
Isolate the variable by dividing each side by factors that don't contain the variable. for z let me know if u need help
Answer:
Hallooooooo
Step-by-step explanation:
Related Questions
a plane intersects one cone of a double-napped cone such that the plane is perpendicular to the axis. what conic section is formed?
Answers
When a plane intersects a double-napped cone such that the plane is perpendicular to the axis, the conic section formed is a circle.
A double-napped cone is a cone that has two identical, symmetrical, curved sides that meet at a common point called the vertex. The axis of a double-napped cone is a straight line that passes through the vertex and the center of the base.
When a plane intersects a double-napped cone, the conic section formed will depend on the angle between the plane and the axis of the cone. If the plane is perpendicular to the axis, the conic section formed will be a circle. If the plane is not perpendicular to the axis, the conic section formed will be an ellipse, a parabola, or a hyperbola.
In this case, the plane is perpendicular to the axis of the cone, so the conic section formed is a circle.
let f (x) = x e^2x. find a formula for the nth derivative of f, where n is any positive integer. use x and n in your answer if needed.F^(n) (x) =
Answers
The formula for the nth derivative of f(x) = x e^2x is:
F^(n) (x) = n! e^2x + 2n x e^2x
To find the nth derivative of f(x) = x e^2x, we can use the product rule and the chain rule. The product rule states that the derivative of a product of two functions is the first function times the derivative of the second function plus the second function times the derivative of the first function.
The chain rule states that the derivative of a composition of functions is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
Using the product rule, the first derivative of f(x) is:
f'(x) = (1)(e^2x) + (x)(2e^2x) = e^2x + 2xe^2x
For the second derivative, we apply the product rule again:
f''(x) = (2e^2x) + (2e^2x) + (2e^2x) = 4e^2x + 4xe^2x
We can see a pattern forming. The nth derivative of f(x) will have the form:
f^(n)(x) = n! e^2x + 2n x e^2x
This formula includes the terms x and n, as requested in the question.
For more similar questions on derivative:
brainly.com/question/23819325
#SPJ11
help!!!!!!!!!!!!!!!!!!
Answers
Answer:
(c) 329 miles
Step-by-step explanation:
You want to evaluate the expression 5w² -4y²/z³ -56 for (w, y, z) = (9, 25, 5).
EvaluationPut the values where the corresponding variables are and do the arithmetic.
diameter = 5(9²) -4(25)²/(5)³ -56
diameter = 5(81) -4(625)/125 -56 = 405 -20 -56
diameter = 329 . . . . miles
<95141404393>

Find the areas of the shaded regions in circle with angle 72° 72° and 10 inches
Answers
The areas of the shaded regions in circle is 15π inches².
The area of a circle is given by the formula A = πr²
where:
r = radius of the circle
In this case, the radius is 10 inches. The area of the shaded region can be found by subtracting the area of the smaller sector from the area of the larger sector.
First, find the area of the larger sector. The central angle of this sector is 72°, so the area of the sector is given by:
A = (72°/360°)πr²
A = (72°/360°) π (10 inches)²
A = (1/5)π(100 inches²)
A = 20π inches²
Next, find the area of the smaller sector. The central angle of this sector is also 72°, so the area of the sector is given by:
A = (72°/360°)πr²
A = (72°/360°)π(5 inches)²
A = (1/5)π(25 inches²)
A = 5π inches²
Finally, subtract the area of the smaller sector from the area of the larger sector to find the area of the shaded region:
A = 20π inches² - 5π inches²
A = 15π inches²
Learn more about Area of Circle here: brainly.com/question/28642423
#SPJ11
please help me with 4x+10=-26
Answers
-10 -10
___________
4x = -36
__ ___
4 4
X = -9
Answer:
x=9
Step-by-step explanation:
Solving for x
4x+10=-26
-10 -10
4x=-36
-----------
4 4
x=9
10-(2): a general contracting firm experiences cost overruns on 20% of its contracts. in a company audit, 20 contracts are sampled at random. a. what is the probability that exactly four of them experience cost overruns? b. what is the probability that fewer than three of them experience cost overruns? c. what is the probability that none of them experience cost overruns? d. find the mean number that experience cost overruns. e. find the standard deviation of the number that experience cost overruns.
Answers
a. To find the probability that exactly four of the contracts experience cost overruns, we use the binomial probability formula:
P(X = 4) = (20 choose 4) * 0.2^4 * (0.8\()^16\)
where "X = the number of contracts that experience cost overruns". Using a calculator, we get:
P(X = 4) ≈ 0.2835
b. To find the probability that fewer than three of the contracts experience cost overruns, we need to find the probability that 0, 1, or 2 contracts experience cost overruns. We can use the binomial probability formula for each of these values and add the probabilities together:
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
= (20 choose 0) * 0.2^0 * (0.8)^20 + (20 choose 1) * 0.\(2^1\) * (0.8\()^19\) + (20 choose 2) * 0.\(2^2\) * (0.8\()^18\)
Using a calculator, we get:
P(X < 3) ≈ 0.1792
c. To find the probability that none of the contracts experience cost overruns, we use the binomial probability formula:
P(X = 0) = (20 choose 0) * 0.2^0 * (0.8)^20
Using a calculator, we get:
P(X = 0) ≈ 0.0115
d. The mean number of contracts that experience cost overruns is given by the formula:
μ = n*p
where "n" is the number of contracts sampled (20) and "p" is the probability of a cost overrun (0.2). Thus, we have:
μ = 20 * 0.2
μ = 4
e. The standard deviation of the number of contracts that experience cost overruns is given by the formula:
σ = sqrt(np(1-p))
Plugging in the values, we get:
σ = sqrt(200.2(1-0.2))
σ ≈ 1.79
Learn more about probability
https://brainly.com/question/30034780
#SPJ4
Please help asap. Look at picture

Answers
Answer:
corresponding angles
Step-by-step explanation:
There are 12 students in a high school senior class in how many ways could the yearbook choose the winners of Most Athletic Class
Clown Best School Spirit, Best Looking and Most Likely to Succeed?
Answers
Answer:
28(27)(26) assuming that nobody can get multiple designations.
Step-by-step explanation:
Solve for DE?
Thank you in advance!

Answers
Answer:
he answer is in the image
Step-by-step explanation:

Let R(s, t) = F(u(s, t), v(s, t)), and assume the following are true.
u(1, 0) = 2
us(1, 0) = −2
ut(1, 0) = 6
v(1, 0) = 3
vs(1, 0) = 5
vt(1, 0) = 4
Fu(2, 3) = −1
Fv(2, 3) = 10
Find the values below.
Rs(1, 0) =
Rt(1, 0) =
Answers
Answer:
To find Rs(1,0) and Rt(1,0), we need to use the chain rule of partial differentiation.
Rs(1,0) can be found by computing the partial derivative of R with respect to s, while holding t constant and then evaluating the result at (1,0). Similarly, Rt(1,0) can be found by computing the partial derivative of R with respect to t, while holding s constant and then evaluating the result at (1,0).
Using the chain rule, we have:
Rs = Fu * us + Fv * vs
Rt = Fu * ut + Fv * vt
We are given the values of u, v, us, ut, vs, vt, Fu, and Fv at the point (1,0) and the values of u and v at the point (2,3). We can use these values to compute Rs(1,0) and Rt(1,0) as follows:
Rs(1,0) = Fu(2,3) * us(1,0) + Fv(2,3) * vs(1,0)
= (-1) * (-2) + (10) * (5)
= 52
Rt(1,0) = Fu(2,3) * ut(1,0) + Fv(2,3) * vt(1,0)
= (-1) * (6) + (10) * (4)
= 34
Therefore, Rs(1,0) = 52 and Rt(1,0) = 34
The 3rd and the 6th terms of an Arithmetic Progresion (A.P) are 16 and 34 respectively. Find the sum of the first 6 terms
Answers
Answer:
a(first term)=4
d(common difference)=6
sum of first 6 terms=114

The sum of the first 6 terms is given by 114
What is an Arithmetic progression?An Arithmetic progression (AP) is a special type of progression in which the difference between two consecutive terms is always a constant. The terms of an arithmetic progression series is a a+d, a + 2d, a + 3d, a + 4d, a + 5d,…
Given here The 3rd and the 6th terms of an Arithmetic Progression (A.P) are 16 and 34 respectively. Here on increase in 3 terms the value changes by 34-16=18 Thus if we move by +1 term the common difference must be 18/3=6 and thus the common difference is equal to 3.
∴ The Arithmetic progression is given by:
4,10,16,22,28,34 . . . .
∴ The sum of the first 6 terms is 4+10+16+22+28+34=114
Hence, The sum of the first 6 terms is given by 114
Learn more about an Arithmetic progression here:
https://brainly.com/question/1610404
#SPJ2
i need help with this problem

Answers
Answer:
32.83= 15(x) +1.93
32.83- 1.93= 30.90
30.9= 15x
30.9/ 15 =2.06
X= 2.06
Which means each bottled juice cost 2.06 each
Step-by-step explanation:
A 24 ounce bottle of apple juice is $5.52. A 32 ounce bottle of apple juice is $8.00. Which bottle of apple juice is a better deal? Explain your answer
Answers
Answer:
32 ounce because its more apple juice and only 3 dollars more
Step-by-step explanation:
-(2x+7=-(2x+7) how many solutions
Answers
Hope this helps ;)
g exercise 1. design the sample space ?, the state space s and explain why each xk is a random variable. why is x d fxkgk2n a stochastic process?
Answers
The sample space is the set of all possible outcomes of a random experiment. The state space is the set of all possible values that a random variable can take on.
Each xk is a random variable because it is a function that assigns a numerical value to each element in the sample space. In other words, for each outcome in the sample space, there is a corresponding value of xk.
A stochastic process is a collection of random variables defined on a common sample space. In this case, x d fxkgk2n is a stochastic process because it is a collection of random variables (x1, x2, ..., xn) defined on a common sample space.
A stochastic process can also be defined as a family of random variables {X(t)}, indexed by a set of indices, usually taken as time t. The set of all possible values of the indices is called the parameter space.
For example, in the case of X d fxkgk2n, the parameter space is the set of integers {1, 2, ..., n}.
A stochastic process describes how a system evolves over time. It can be used to model various phenomena, such as stock prices, weather patterns, and population dynamics. The properties of a stochastic process, such as stationarity and independence, can provide insight into the underlying dynamics of the system it models.
To learn more about sample space, use the link:
brainly.com/question/24273864
#SPJ4
10v2 + 50
o Linear binomial
o Constant binomial
Quadratic binomial
Quadratic trinomial
Answers
Answer:
what is the question? probably describe the polynomial. okay. the polynomial 10v^2 + 50 is a quadratic (it is to the 2nd power) and a binomial (has 2 terms).
pls help and show ur work pls

Answers
What is the smallest number of degrees it could be rotated?

Answers
Answer:
180° is the smallest number of degrees it could be rotated.
PLEASE MARK IT THE BRAINLIEST!!!!!
Find the surface area of a regular hexagonal pyramid with side length = 8, and a slant height = 16. Round to the nearest tenth.
Answer Immediately
Answers
Answer:
To find the surface area of a regular hexagonal pyramid, we need to find the area of the six triangular faces and the area of the hexagonal base, and then add them together.
The area of each triangular face is given by the formula:
(1/2) x base x height
In this case, the base of each triangle is the side length of the hexagon (8), and the height is the slant height of the pyramid (16). Therefore, the area of each triangular face is:
(1/2) x 8 x 16 = 64
The hexagonal base can be divided into six equilateral triangles, each with side length 8. The area of each equilateral triangle is:
(1/4) x sqrt(3) x side length^2
Plugging in the values, we get:
(1/4) x sqrt(3) x 8^2 = 16sqrt(3)
To find the total surface area, we add the area of the six triangular faces and the area of the hexagonal base:
6 x 64 + 16sqrt(3) = 384 + 16sqrt(3)
Rounding to the nearest tenth, the surface area of the regular hexagonal pyramid is:
398.6 square units (rounded to one decimal place)
PLEASE HELP DUE BY MIDNIGHT! Prove that the top card matches the bottom. Trigonometry. THANK YOU!

Answers
\(\textit{Pythagorean Identities} \\\\ \sin^2(\theta)+\cos^2(\theta)=1\implies \cos^2(\theta )=1-\sin^2(\theta ) \\\\ 1+\cot^2(\theta)=\csc^2(\theta) \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \cfrac{1-\sin^2(\theta )}{1+\cot^2(\theta )}~~ = ~~\sin^2(\theta )\cos^2(\theta ) \\\\[-0.35em] ~\dotfill\\\\ \cfrac{1-\sin^2(\theta )}{1+\cot^2(\theta )}\implies \cfrac{\cos^2(\theta )}{\csc^2(\theta )}\implies \cfrac{\cos^2(\theta )}{ ~~ \frac{1}{\sin^2(\theta )} ~~ }\implies \cos^2(\theta )\sin^2(\theta )\)
consider the vectors v1, v2, v3 in r2 (sketched in the accompanying figure). vectors v1 and v2 are parallel. how many solutions x, y does the system xv1 yv2 = v3 have? argue geometrically.
Answers
There is exactly one solution if v3 lies on this line, and no solution otherwise.
Given: vectors v1, v2, v3 in R2
We know that the vectors v1 and v2 are parallel, and we are asked to find the number of solutions of the system xv1 + yv2 = v3. We will argue geometrically.
Let us say that v1 and v2 are not equal to zero and are parallel to the x-axis. We can then write:
v1 = (a, 0)
v2 = (b, 0)
where a and b are nonzero constants. Since v1 and v2 are parallel, their cross-product is zero:
v1 × v2 = a*0 - 0*b = 0
This means that v1 and v2 are linearly dependent. Thus, we can express v2 as a scalar multiple of v1:
v2 = k*v1
where k is a nonzero constant. We can then substitute these expressions into the system and solve for x and y:
xv1 + yv2 = v3
xv1 + y(k*v1) = v3
(x + ky)v1 = v3
Since v1 is nonzero, the equation has a unique solution if and only if (x + ky) is nonzero. But (x + ky) is zero if and only if x = -ky, which is the equation of a line passing through the origin and perpendicular to v1 and v2. Thus, there is exactly one solution if v3 lies on this line, and no solution otherwise.
To see this geometrically, we can sketch the vectors v1, v2, and v3, and the line passing through the origin and perpendicular to v1 and v2. If v3 lies on this line, then there is exactly one solution, which corresponds to the intersection of the line and the vector v3. If v3 does not lie on this line, then there is no solution, since the line does not pass through v3.
Know more about vectors here,
https://brainly.com/question/24256726
#SPJ11
Please help me
I need help fast!

Answers
Answer:
code = 4488.24
A = 1006.76
B = 2893.82
C = 2712.96
D = 111.78
Step-by-step explanation:
Volume of a cylinder = πr²h
where r = radius and h = height
A) radius = diameter / 2 = 15 / 2 = 7.5
height = 5.7
==> volume = 3.14(7.5)²5.7
==> volume = 3.14(56.26)5.7
==> volume = 176.625 × 5.7
==> volume = 1006.7625
==> volume = 1006.76
B) radius = 8 and height = 14.4
==> volume = 3.14(8)²14.4
==> volume = 3.14(64)14.4
==> volume = 200.96(14.4)
==> volume = 2893.82
C) radius = 6 and height = 24
==> volume = 3.14(6)²24
==> volume = 3.14(36)24
==> volume = 113.04 × 24
==> volume = 2712.96
D) radius = 2 and height = 8.9
==> volume = 3.14(2)²8.9
==> volume = 3.14(4)8.9
==> volume = 12.56(8.9)
==> volume = 111.78
Code ( B + C ) - ( D + A )
A = 1006.76 , B = 2893.82 , C = 2712.96 , D = 111.78
Code : ( 2893.82 + 2712.96 ) - ( 111.78 + 1006.76 )
==> add values in parenthesis
Code : 5606.78 - 1118.54
==> subtract values
Code : 4488.24
You may need to vse the approgrite appendix table to answer this question. television vieving pee household (a) What it the probablity that a household vieas television between 4 and 10 houts a day? (Round your answer to four decimal placet.) hin (c) What is the peobabitity that a houschold views televisian more than 3 hours a day? (Round your answer to four decimal niaces.)
Answers
(a) The probability that a household views television between 4 and 10 hours a day is 0.0833.
(c) The probability that a household views television more than 3 hours a day is 0.6944.
The appendix table shows the probability that a household views television for a certain number of hours per day. To find the probability that a household views television between 4 and 10 hours a day, we can add the probabilities that the household views television for 4 hours and 5 hours, and 6 hours, and 7 hours, and 8 hours, and 9 hours, and 10 hours. The sum of these probabilities is 0.0833.
To find the probability that a household views television more than 3 hours a day, we can add the probabilities that the household views television for 4 hours, 5 hours, 6 hours, 7 hours, 8 hours, 9 hours, and 10 hours. The sum of these probabilities is 0.6944.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
Can someone PLEASE help me ASAP?? It’s due today!! i will give brainliest if it’s correct!!
please do part a, b, and c!!

Answers
Answer:
a = 10.5 b = 8
Step-by-step explanation:
a). Range = Biggest no. - Smallest no.
= 10.5 - 0 = 10.5
b). IQR = 8 - 0 = 8
c). MAD means mean absolute deviation.
Pls I need help ASAP!!!!!

Answers
( 5,0 ) and ( 0,4 ) are the x and y-intercept of the function 4x + 5y = 20 respectively.
How to solve for x and y-intercept?The intercept of a line on a graph is simply the point at which it intersects either the x-axis or y-axis.
Given the data in the question;
4x + 5y = 20Input value when output is 0 = ?Output value when input is 0 = ?Now, we find the intercepts of the equation of line, plug in y = 0 and solve for x
4x + 5y = 20
4x + 5(0) = 20
4x = 20
x = 20/4
x = 5
Hence, the x-intercept is ( 5,0 )
For the y-intercept, plug in x = 0 and solve for y
4(0) + 5y = 20
5y = 20
y = 20/5
y = 4
Hence, the y-intercept is ( 0,4 ).
Therefore the x and y-intercept are ( 5,0 ) and ( 0,4 ).
Learn more about intercepts here: https://brainly.com/question/16861385
#SPJ1

PLZ HELP ME WITH THS
Larry has already run 16 miles on his own, he expects to run 9 miles during each track practice. how many track practices would it take for Larry to run 43 miles?
Answers
Answer: 3 track practices
Step-by-step explanation:
X= (# of track practices)
16 + 9x=43
9x=27
x=3
Answer:
Step-by-step explanation:
given the derivative of the function f(x) is f′(x)=2x2−2x−60, which of the following statements is true?
a. f(x) has an inflection point at x b. f(x) has an inflection point at x = 2 c. f(x) has a local minimum at x = -5. d. f(x) has a local minimum at x = -6 e. f(x) has a local maximum at x = 6/ a
Answers
we cannot determine whether `f(x)` has a local maximum at `x = 6/a`.Thus, the correct option is C: `f(x)` has a local minimum at `x = -5`.
We know that the derivative of a function provides information about the slope of the graph of that function. Hence, we can use the information provided by the derivative of a function to make certain conclusions about the shape and behavior of the graph of that function.Now, given the derivative of the function f(x) is `f′(x) = 2x² − 2x − 60`. Let us find the second derivative of this function as follows:
`f′(x) = 2x² − 2x − 60`
Differentiating `f′(x)`, we get: `f′′(x) = 4x − 2`Now, let's discuss each option one by one:Option A: `f(x)` has an inflection point at `x`.We can conclude this by finding the point where the concavity of the function changes, i.e., the point where `f′′(x)` changes sign. For this function, `f′′(x) = 4x − 2`.We have to solve the inequality `f′′(x) < 0` for `x`. `4x − 2 < 0 ⇒ x < 1/2`Therefore, the function `f(x)` is concave down for `x < 1/2` and concave up for `x > 1/2`.Thus, the function has an inflection point at `x = 1/2`.So, this option is incorrect.Option B: `f(x)` has an inflection point at `x = 2`.We have already seen that the function has an inflection point at `x = 1/2`. So, this option is incorrect.Option C: `f(x)` has a local minimum at `x = -5`.To find the local minimum of the function, we have to find the critical points of the function. These are the points where `f′(x) = 0` or `f′(x)` is undefined. Here, `f′(x) = 2x² − 2x − 60`.We have to solve the equation `f′(x) = 0` for `x`. `2x² − 2x − 60 = 0 ⇒ x² − x − 30 = 0 ⇒ (x − 6)(x + 5) = 0`So, the critical points are `x = 6` and `x = -5`.We can find the nature of these critical points by analyzing the sign of `f′(x)` on either side of the critical points: On the interval `(-∞,-5)`, `f′(x) < 0`. On the interval `(-5,6)`, `f′(x) > 0`.On the interval `(6,∞)`, `f′(x) > 0`.So, `x = -5` is a local maximum and `x = 6` is a local minimum.Therefore, the option C is correct.Option D: `f(x)` has a local minimum at `x = -6`.This option is incorrect as the function has a local minimum at `x = 6`, not `x = -6`.Option E: `f(x)` has a local maximum at `x = 6/a`.As the value of `a` is not known, we cannot determine the value of `6/a`.
\To know more about derivative:
https://brainly.com/question/29144258
#SPJ11
Round the number to 3
significant figures.
0.2590100

Answers
Answer:
0.259
Step-by-step explanation:
There are some rules in determining what numbers are significant figures.
All non-zero numbers are significant.Zeroes between two non-zero numbers are significant.Zeroes at the front of a number are not significant.Trailing zeroes are only significant if there is a decimal point.We can determine how many significant figures the number currently has.
The first zero is not significant.2, 5, 9, and 1 are significant because they are non-zero numbers.The zero between 9 and 1 is significant because it is a captive zero.The zeroes at the end of the number are significant because they are trailing zeroes.There are currently seven significant figures. In order to round the number to three significant figures, we must round it to the thousandths place, or the 9.
The rounding rules are:
If the digit in the place after the number we are rounding is less than 5, you round down (or in other words, keep the number the same; Ex: 74 becomes 70)If that digit is greater than 5, you round up (Ex: 78 becomes 80)Since 0 is less than 5, the number rounded to 3 significant figures is 0.259.
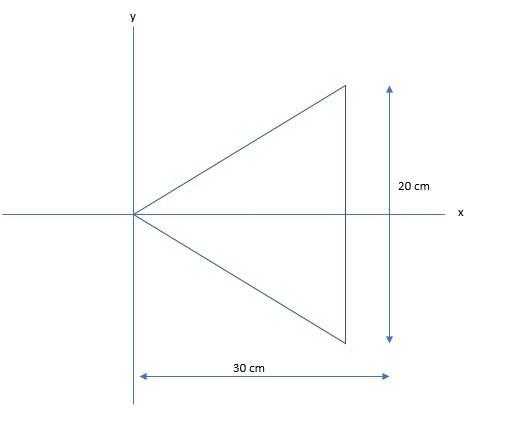
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

A person invested $210 in an account growing at a rate allowing the money to double every 10 years. how long, to the nearest tenth of a year would it take for the value of the account to reach $1,510?
Answers
Answer:
28.5 years
Step-by-step explanation:
You want to know how many years it takes for a $210 investment to have a value of $1510 if it doubles in value every 10 years.
DoublingWhen an account doubles in value in 10 years, its value after t years is given by ...
A = P(2^(t/10))
We have A=1510, P=210, and we want to find t.
Solution1510 = 210(2^(t/10)) . . . . . . use the given values
1510/210 = 2^(t/10) . . . . . divide by 210
Taking logarithms gives ...
log(1510/210) = (t/10)log(2)
Dividing by the coefficient of t, we have ...
t = 10·log(1510/210)/log(2) ≈ 28.46
It would take about 28.5 years for the value of the account to reach $1510.

