Write an equation that passes through a minimum
point of (-3,-2) and a y-intercept at (0,25)
Answers
Answer: y= 9x+ 25
Step-by-step explanation:
to calculate the slope, rise/run rise is difference in y-values 25 -(-2) =27
run is difference in x-values 0-(-3) = 3 . 27/3 = 9
b= y-intercept Given: 25

Related Questions
Can someone please help me?

Answers
Answer:
4
Step-by-step explanation:
It is 4 because there are 4 pea pods with 3 peas in each pod.
Answer:
2
Step-by-step explanation:
assume that 20 parts are checked each hour and that x denotes the number of parts in the sample of 20 that require rework. parts are assumed to be independent with respect to rework. a. if the percentage of parts that require rework remains at 1%, what is the probability that hour 10 is the first sample at which x exceeds 1?
Answers
Answer:
what
Step-by-step explanation:
The probability that hour 10 is the first sample at which x exceeds 1 is 0.0086.
Let X denotes the number of parts in the sample of 20 that require rework. We can model the number X of parts in a random sample of 20 that require rework with a binomial distribution \($X\sim B(20,0.01)$\). We want to find the probability that the first sample at which X exceeds 1 occurs at hour 10. To do this, we need to compute two probabilities:
- The probability that in the first 9 samples, no sample has more than 1 part needing rework.
- The probability that in the 10th sample, there are at least 2 parts needing rework.
To compute the first probability, we use the binomial distribution with n=20 and p=0.01, and note that each of the first 9 samples is independent. Thus, the probability that no sample in the first 9 has more than 1 part needing rework is
\($$P(X\le 1)^9 = \left(\binom{20}{0}(0.01)^0(0.99)^{20} + \binom{20}{1}(0.01)^1(0.99)^{19}\right)^9 \approx 0.435$$\)
To compute the second probability, we just use the binomial probability mass function with n=20 and p=0.01:
\($$P(X\ge 2) = 1 - P(X=0) - P(X=1) \approx 0.0198$$\)
Finally, we can multiply these probabilities to get the desired probability:
\($P(\text{first sample with } X > 1 \text{ is at hour } 10) = 0.435\times 0.0198 \approx \boxed{0.0086}.$\)
To know more about probability: https://brainly.com/question/24756209
#SPJ11
R Given:07F = FRY: RFY: LFY
Prove: AFRY:ΔFLY
STATEMENT REASON
YLF =FRY. 23.
RFY=LFY. GIVEN
FY=FY(underlined) 24.
ΔFRY=ΔFLY. 25.

Answers
S1: ∠YLF ≅ ∠FRY (Given)
S2: ∠RFY ≅ ∠LFY (Given)
S3: FY ≅ FY (Transitive property)
S4: ΔFRY ≅ ΔFLY (AAS theorem)
What is the AAS Congruence Theorem?The AAS congruence theorem states that if two triangles have two pairs of corresponding congruent angles, and a pair of corresponding non-included side that are congruent, then both triangles area congruent.
To prove that ΔFRY ≅ ΔFLY, the proof that shows they are congruent by the AAS congruence theorem is:
S1: ∠YLF ≅ ∠FRY (Given)
S2: ∠RFY ≅ ∠LFY (Given)
S3: FY ≅ FY (Transitive property)
S4: ΔFRY ≅ ΔFLY (AAS theorem)
Learn more about the AAS Theorem on:
https://brainly.com/question/4460411
Determine the input choices to minimize the cost of producing 20 units of output for the production function Q=8K+12L if w=2 and r=4. Use lagrange method in solving the values. Show complete solution.
Answers
Using the Lagrange method, we found that the input choices to minimize the cost of producing 20 units of output are K = 0 and L = 0.
To determine the input choices that minimize the cost of producing 20 units of output for the production function Q=8K+12L, given w=2 and r=4, we can use the Lagrange method of optimization. The Lagrange method involves setting up a Lagrangian function that incorporates the production function, the cost function, and the constraint equation.
Let's denote the cost of production as C, the amount of capital used as K, and the amount of labor used as L. We want to minimize the cost C subject to the constraint of producing 20 units of output.
The Lagrangian function is given by:
L(K, L, λ) = C + λ(Q - 20)
We need to find the critical points of this function with respect to K, L, and λ. Taking partial derivatives and setting them equal to zero, we have:
∂L/∂K = 8 - λ = 0 (1)
∂L/∂L = 12 - λ = 0 (2)
∂L/∂λ = Q - 20 = 0 (3)
From equations (1) and (2), we have λ = 8 and λ = 12. Substituting these values into equation (3), we get Q = 20.
Now, we can solve equations (1) and (2) to find the values of K and L.
From equation (1), we have 8 - 8 = 0, which gives us K = 0.
From equation (2), we have 12 - 12 = 0, which gives us L = 0.
Therefore, the input choices that minimize the cost of producing 20 units of output are K = 0 and L = 0.
In this case, it implies that no capital or labor is required to produce 20 units of output at the given prices of w=2 and r=4. This could indicate a case of technological efficiency or an unrealistic scenario.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
suppose a jar contains 11 red marbles and 40 blue marbles. if you reach in the jar and pull out 2 marbles at random, find the probability that both are red. write your answer as a reduced fraction.
Answers
The required probability that both are red out of total marbles is 0.0431 or 4.31%.
What is probability?A probability is a number that mirrors the opportunity or probability that a specific occasion will happen. Probabilities can be communicated as extents that reach from 0 to 1, and they can likewise be communicated as rates going from 0% to 100 percent.
According to question:Total number of marbles in a jar = 40 + 11 = 51
Number of red marbles = 11, blue marbles = 40
At our first pull, there is an 11/51 chance that a red will be pulled and in second pull the probability is 10/50 , as one red marbles taken out.
Net probability = 11/51×10/50 = 0.0431
percentage probability = 4.31%
To know more about probability visit:
brainly.com/question/15124899
#SPJ4
a die is tossed 180 times with the following results: x 1 2 3 4 5 6 f 28 36 36 30 27 23 is this a balanced die? use a 0.01 level of significance
Answers
Based on the chi-square test, there is no significant evidence to suggest that the die is not balanced.
We have,
To determine if the die is balanced, we can perform a chi-square test of goodness of fit.
The null hypothesis is that the die is balanced, and the alternative hypothesis is that the die is not balanced.
First, let's calculate the expected frequencies for each outcome assuming the die is balanced. Since there are 180 tosses in total, each outcome is expected to have an equal probability of 1/6.
Expected frequency for each outcome
= (Total tosses) x (Probability of each outcome)
Expected frequency for each outcome = (180) x (1/6)
Expected frequency for each outcome = 30
Now, we can calculate the chi-square test statistic using the formula:
χ² = Σ [(Observed frequency - Expected frequency)² / Expected frequency]
Let's calculate the chi-square test statistic:
χ² = [(28 - 30)² / 30] + [(36 - 30)² / 30] + [(36 - 30)² / 30] + [(30 - 30)² / 30] + [(27 - 30)² / 30] + [(23 - 30)² / 30]
χ² = [(-2)² / 30] + [(6)² / 30] + [(6)² / 30] + [(0)² / 30] + [(-3)² / 30] + [(7)² / 30]
χ² = 4/30 + 36/30 + 36/30 + 0/30 + 9/30 + 49/30
χ² = 134/30
χ² ≈ 4.467
Next, we need to compare the calculated chi-square value to the critical chi-square value at a significance level of 0.01 and degrees of freedom equal to the number of outcomes minus 1 (6 - 1 = 5).
Looking up the critical chi-square value in a chi-square distribution table with 5 degrees of freedom and a significance level of 0.01, we find it to be approximately 15.086.
Since the calculated chi-square value (4.467) is less than the critical chi-square value (15.086), we fail to reject the null hypothesis.
Therefore, we do not have sufficient evidence to conclude that the die is not balanced at a 0.01 level of significance.
Thus,
Based on the chi-square test, there is no significant evidence to suggest that the die is not balanced.
Learn more about the chi-square test here:
https://brainly.com/question/30760432
#SPJ1
Consider the equation, y = + 1x1 + 2x2 + u. A null hypothesis, H0: 2 = 0 states that:
x2 has no effect on the expected value of 2.
x2 has no effect on the expected value of y.
2 has no effect on the expected value of y.
y has no effect on the expected value of x2.
Answers
The null hypothesis, H0: 2 = 0, states that the coefficient 2 has no effect on the expected value of y. This means that the expected value of y does not change when x2 is changed.
Mathematically, this can be expressed as:
E[y|x2] = E[y]
Where E[y|x2] is the expected value of y when x2 is given, and E[y] is the expected value of y when x2 is not given.
The equation for y can be rewritten as:
y = 1x1 + 0x2 + u
Where 0 is the coefficient of 2 when the null hypothesis is true. This equation can be further simplified to:
y = 1x1 + u
The equation now shows that x2 has no effect on the expected value of y. This is because the coefficient of x2 is 0, meaning that no matter what value x2 is given, it will not affect the expected value of y. Therefore, the null hypothesis, H0: 2 = 0 states that x2 has no effect on the expected value of y.
Learn more about null hypothesis here:
https://brainly.com/question/28920252
#SPJ4
What is the volume of the prism?
15 cm
7 cm
9 cm
12 cm
Answers
Answer:
Just simply look up how to find the volume of a prism and the answer will immediately come to your head you'll get the right answer.
Step-by-step explanation:
which equation results from applying the secant and tangent segment theorem to the figure?12(a 12)
Answers
This simplifies to:
a² = 12x + 144
This is the equation that results from applying the Secant-Tangent Segment Theorem to the given figure.
Let's first define the terms and state the Secant-Tangent Segment Theorem.
1. Equation: A mathematical statement that shows the equality of two expressions.
2. Secant: A line that intersects a circle at two points.
3. Tangent: A line that touches a circle at only one point, without crossing it.
Secant-Tangent Segment Theorem: If a secant and a tangent are drawn from a point outside a circle, the product of the length of the secant segment and its external part is equal to the square of the length of the tangent segment.
Let's represent the given lengths as follows:
- Length of tangent segment = a
- Length of secant segment (inside the circle) = 12
- Length of the external part of the secant segment (outside the circle) = x
According to the Secant-Tangent Segment Theorem, the equation is:
(a)(a) = (12)(x + 12)
This simplifies to:
a² = 12x + 144
This is the equation that results from applying the Secant-Tangent Segment Theorem to the given figure.
Visit here to learn more about Secant-Tangent Segment Theorem:
brainly.com/question/26407978
#SPJ11
can you please help

Answers
Answer:
0
8
10
Then make thoes ordered pairs so;
(0,0)
(4,8)
(5,10)
Answer:
0,8,10 i think you plug in 0 for x and do the same for the
others
Derek will deposit $6,460.00 per year for 21.00 years into an
account that earns 14.00%, The first deposit is made next year. How
much will be in the account 40.00 years from today? Answer format:
Cur
Answers
The total amount that will be in the account 40.00 years from today, considering the annual deposits of $6,460.00 for 21.00 years and an annual interest rate of 14.00%, will be approximately $6,120,433.84.
Derek plans to deposit $6,460.00 per year for 21.00 years into an account with an annual interest rate of 14.00%. The first deposit will be made next year.
To calculate the total amount in the account 40.00 years from today, we need to consider the annual deposits, the interest earned, and the compounding effect over the years.
The annual deposit is $6,460.00, and the duration of deposits is 21.00 years.
Therefore, the total amount of deposits made over the 21.00 years will be 21.00 × $6,460.00 = $135,660.00.
To calculate the future value of the deposits and the interest earned, we can use the compound interest formula:
Future Value = Principal × \((1 + interest\, rate)^{number\, of\, periods}\)
In this case, the principal is $135,660.00, the interest rate is 14.00%, and the number of periods is 40.00 years.
Future Value = $135,660.00 × \((1 + 0.14)^{40}\)
Future Value = $135,660.00 × \((1.14)^{40}\)
Future Value = $135,660.00 × 45.094
Future Value = $6,120,433.84
Therefore, the total amount that will be in the account 40.00 years from today, considering the annual deposits of $6,460.00 for 21.00 years and an annual interest rate of 14.00%, will be approximately $6,120,433.84.
Learn more about compound interest formula here:
https://brainly.com/question/29008279
#SPJ11
In this number tree, the integers greater than or equal to 0 are written out in increasing order, with the top row containing one integer and every row after containing twice as many integers as the row above it. If row 1 contains the integer 0, what is the fifth number in row 10?
Answers
Answer:
The fifth integer in row 10 using the number tree pattern is 515.
Step-by-step explanation:
The attached picture is instrumental to understanding the solution to this. There are different methods to approach this problem. But we will use observations to solve the problem.
Looking at the tree diagram, we see that the first row has 1 integer, the second has 2, the third has 4 and the fourth has 8. From here, we can see that a row has 2^n numbers where n = 0, 1, 2, 3, 4, . . .
Row 1 = 2^0 = 1 number
Row 2 = 2^1 = 2 numbers
Row 3 = 2^2 = 4 numbers
Row 4 = 2^3 = 8 numbers. And so on.
Also we notice that the last number in row 4 is 14. This can be gotten by adding the total number of numbers from row 1 to row 4 which is
1 + 2 + 4 + 8 = 15 but the first number on the chart is 0 which means we have to take out the first integer to get the last integer on row 4. Doing this, we have 14.
Since our aim is to know the fifth number in row 10, then we need to know the last number in row 9 then count from the first number in row 10 to the fifth. Using 2^n to get the number of numbers in each row like we've done above we can add the number of numbers to know the total numbers we have from row 1 to row 9 as follows:
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 = 511
As we've said previously, 0 is the first integer in the tree and should be removed to know the last number in row 9. This would be 510.
If 510 is the last number in row 9 is 510, then the first number in row 10 would be 511. Counting to the fifth number we get to 515. Thus the fifth number in row 10 using the number tree pattern is 515.

The store offers in-house financing. Why would the store want to do something like that?
Answers
Answer:because it just a word problem
Step-by-step explanation:
like i said it just a word problem
WILL MARK BRAINLIEST! Determine the quadratic function of the form f(x)= a(x - h)² + k whose graph is given on the
right.

Answers
Answer:the quadratic function in f(x)= a(x-h)^2+k is f(x) = - (x - 2)² + 2.I think this is false";}
Step-by-step explanation:
For the following set of data, find the percentage of data within 2 population standard deviations of the mean, to the nearest percent
chart is in the photo

Answers
Percentage of data within 2 population standard deviations of the mean is 68%.
To calculate the percentage of data within two population standard deviations of the mean, we need to first find the mean and standard deviation of the data set.
The mean can be found by summing all the values and dividing by the total number of values:
Mean = (20*2 + 22*8 + 28*9 + 34*13 + 38*16 + 39*11 + 41*7 + 48*0)/(2+8+9+13+16+11+7) = 32.68
To calculate standard deviation, we need to calculate the variance first. Variance is the average of the squared differences from the mean.
Variance = [(20-32.68)^2*2 + (22-32.68)^2*8 + (28-32.68)^2*9 + (34-32.68)^2*13 + (38-32.68)^2*16 + (39-32.68)^2*11 + (41-32.68)^2*7]/(2+8+9+13+16+11+7-1) = 139.98
Standard Deviation = sqrt(139.98) = 11.83
Now we can calculate the range within two population standard deviations of the mean. Two population standard deviations of the mean can be found by multiplying the standard deviation by 2.
Range = 2*11.83 = 23.66
The minimum value within two population standard deviations of the mean can be found by subtracting the range from the mean and the maximum value can be found by adding the range to the mean:
Minimum Value = 32.68 - 23.66 = 9.02 Maximum Value = 32.68 + 23.66 = 56.34
Now we can count the number of data points within this range, which are 45 out of 66 data points. To find the percentage, we divide 45 by 66 and multiply by 100:
Percentage of data within 2 population standard deviations of the mean = (45/66)*100 = 68% (rounded to the nearest percent).
Therefore, approximately 68% of the data falls within two population standard deviations of the mean.
for more such questions on population
https://brainly.com/question/30396931
#SPJ8
Given the functions f(x) = 3x - 1 and g(x) = 3x + 4, which operation results in the smallest coefficient on the x term?
Answers
The operation of Subtraction can be used to result in the smallest co-efficient term on the x term.
In the given question, Two functions are given f(x) = 3x - 1, and g(x) = 3x + 4. Now we have to find out which mathematical operation results in the smallest co-efficient term on x. We know that the basic Operations are:
AdditionSubtractionMultiplicationDivision=> Now, we use the operation of Subtraction for the two functions. Which can be calculated by: f(x) - g(x), Calculating we get:
=> (3x - 1) - (3x - 4)
=> 3x -1 -3x + 4
=> 3
Here we get the Coefficient of x = 0 which is the lowest.
Hence, Subtraction will be used
To know more about Mathematical Operations, Click here:
https://brainly.com/question/12210310
#SPJ9
A quality control expert at LIFE batteries wants to test their new batteries. The design engineer claims they have a variance of 84648464 with a mean life of 886886 minutes. If the claim is true, in a sample of 145145 batteries, what is the probability that the mean battery life would be greater than 904.8904.8 minutes
Answers
We can conclude that it is extremely unlikely to obtain a sample mean greater than 904.8 minutes if the design engineer's claim about the population variance and mean is true.
We can use the Central Limit Theorem to approximate the distribution of the sample means.
Under the given assumptions, the mean of the sampling distribution of the sample means is equal to the population mean, which is 886886 minutes, and the standard deviation of the sampling distribution of the sample means is equal to the population standard deviation divided by the square root of the sample size, which is\(\sqrt{84648464/145145} = 41.77\) minutes.
Therefore, we can standardize the sample mean using the formula:
\(z = (\bar{x} - \mu) / (\sigma / \sqrt{n } )\)
where \(\bar{x}\) is the sample mean, \(\mu\) is the population mean, sigma is the population standard deviation, and n is the sample size.
Plugging in the values we get:
z = (904.8 - 886886) / (41.77) = -21115.47
The probability of getting a sample mean greater than 904.8 minutes can be calculated as the area under the standard normal curve to the right of z = -21115.47.
This probability is essentially zero, since the standard normal distribution is symmetric and nearly all of its area is to the left of -6.
Foe similar question on sample mean.
https://brainly.com/question/29368683
#SPJ11
Write and solve an equation for .

Answers
Answer:
\(x = 40 \: \: degrees\)
Step-by-step explanation:
\(3x + 20 + x = 180 \\ 4x + 20 = 180 \\ 4x = 180 - 20 \\ 4x = 160 \\ \frac{4x}{4} = \frac{160}{4} \\ x = 40 \: \: degrees\)
Find the product
(3c-5)(c+3)
Answers
Answer:
3c2 + 4c − 15
Step-by-step explanation:
I tried my best if this is correct please sub to m YT I am a aspiring small creator
my YT is YoungGodlyFN.
Applying distributive property, the product of the given expression,
(3c-5)(c+3) is 3c² + 4c - 15.
In mathematics, the outcome of multiplying two integers is their product.
The given expression is,
(3c-5)(c+3)
Expanding this expression as,
3c(c+3) - 5(c+3)
Distribute the number inside the bracket we get,
3c² + 3x3c - 5c - 5x3
⇒ 3c² + 9c - 5c - 15
Combine like terms,
3c² + (9 - 5)c - 15
⇒ 3c² + 4c - 15
Thus,
(3c-5)(c+3) = 3c² + 4c - 15
Hence,
The product of the given expression is 3c² + 4c - 15.
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ6
Deal 1: $16.05 for 5 Caramel apples Deal 2: $19.14 for 6 caramel
Answers
Which inequality represents all values of x for which the product below is
defined

Answers
Answer:
D
Step-by-step explanation:
D is the only option where there's always 0 or positive integers inside the radical. The square root of a negative number is imaginary.
20 is about what percent of 52
Answers
Answer:
To get the solution, we are looking for, we need to point out what we know.
1. We assume, that the number 52 is 100% - because it's the output value of the task.
2. We assume, that x is the value we are looking for.
3. If 52 is 100%, so we can write it down as 52=100%.
4. We know, that x is 20% of the output value, so we can write it down as x=20%.
5. Now we have two simple equations:
1) 52=100%
2) x=20%
where left sides of both of them have the same units, and both right sides have the same units, so we can do something like that:
52/x=100%/20%
6. Now we just have to solve the simple equation, and we will get the solution we are looking for.
7. Solution for what is 20% of 52
52/x=100/20
(52/x)*x=(100/20)*x - we multiply both sides of the equation by x
52=5*x - we divide both sides of the equation by (5) to get x
52/5=x
10.4=x
x=10.4
now we have:
20% of 52=10.4
Step-by-step explanation:
David is paid a salary of $1850 per month. He is also paid time and a half for work in excess of 40 hours a week. He worked 62 hours last week. What is his gross pay?
Answers
Answer:
$1,471.5625
Step-by-step explanation:
Monthly salary = $1850
Weekly salary = $1850/4 weeks
= $462.5
Hourly rate = $462.5/40 hours
= $11.5625
Overwork time = 62 hours - 40 hours
= 22 hours
Time and a half = 1.5 times the normal salary
Overwork time payment per hour = 1.5 × $11.5625
= $17.34375
Overwork time payment for 22 hours = 22 × $17.34375
= $381.5625
Last week salary = weekly salary + overtime payment
= $462.5 + $381.5625
= $84.0625
Gross salary for the month = 3 weeks regular salary + last week salary
= (3 × $462.5) + $84.0625
= $1387.5 + $84.0625
= $1,471.5625
Security A and B have a covariance of 450%2. Security A is estimated to have a variance of 900%2. The correlation between the two securities is 0.8. What is the standard deviation of security B?
A) Cannot be computed with the information provided
B) 225%2
C) 15%
D) 18.75%
E) 62.5%
Answers
The standard deviation of security B, the answer is option D, 18.75%.
Given that Security A and B have a covariance of 450%2,
Security A is estimated to have a variance of 900%2,
and the correlation between the two securities is 0.8.
We know that the covariance between Security A and B is given as;
Cov(A,B) = p(A,B)σAσB, where p(A,B)
is the correlation between A and B, σA is the standard deviation of A, and σB is the standard deviation of B.
Therefore, the standard deviation of Security B is given by;
σB = Cov(A,B)/[p(A,B)σA]
= (450%2)/[0.8 × (900%2)1/2]
= (450%2)/[0.8 × (900)1/2]%
≈ 18.75%.
Therefore, the answer is option D, 18.75%.
To know more about standard deviation click here:
https://brainly.com/question/12402189
#SPJ11
Given that a function, g, has a domain of -1 ≤ x ≤ 4 and a range of 0 ≤ g(x) ≤ 18 and that g(-1) = 2 and g(2) = 8, select the statement that could be true for g.
Answers
Options
(A)g(5) = 12 (B)g(1) = -2 (C)g(2) = 4 (D)g(3) = 18Answer:
(D)g(3) = 18
Step-by-step explanation:
Given that the function, g, has a domain of -1 ≤ x ≤ 4 and a range of 0 ≤ g(x) ≤ 18 and that g(-1) = 2 and g(2) = 8
Then the following properties must hold
The value(s) of x must be between -1 and 4The values of g(x) must be between 0 and 18.g(-1)=2g(2)=9We consider the options and state why they are true or otherwise.
Option A: g(5)=12
The value of x=5. This contradicts property 1 stated above. Therefore, it is not true.
Option B: g(1) = -2
The value of g(x)=-2. This contradicts property 2 stated above. Therefore, it is not true.
Option C: g(2) = 4
The value of g(2)=4. However by property 4 stated above, g(2)=9. Therefore, it is not true.
Option D: g(3) = 18
This statement can be true as its domain is in between -1 and 4 and its range is in between 0 and 18.
Therefore, Option D could be true.
Answer: g(3) =18
Step-by-step explanation: thats probably all you need
what is 58/71= (round to the nearest HUNDREDST PLACE)
Answers
Answer:
817 10^-3
Step-by-step explanation:
58/71
0.817
817 10^-3
Answer:
0.82
Step-by-step explanation:
The question asks to change 58/71 to a decimal, then round it off to the nearest hundredst.
To change it to a decimal, divide the denominator(71) by the numerator(58)
71/58=0.81690
Then, round off to the nearest hundrest place would be to a number in which the numbers after a decimal would form a fraction with the denominator being 100 that number would be 0.81(ignore every digit after the third number after the decimal place)
if you left the answer like this, it would be wrong. You have to consider the number after the 'rounded off decimal' which is 6. If the number is 5 or higher, add 1 to the previous number.
6 is higher than 5, so we round it off as 1
hence= 0.816 ... 0.8(+1)
Hope this helps
I need help, correct answer will get brainliest!
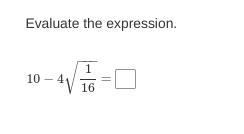
Answers
Answer:
9
Step-by-step explanation:
1/16 square rooted = .25 * 4 = 1 then 10-1=9
after running a classification model, we have the following confusion matrix: confusion matrix what is this model's overall accuracy ?
Answers
The overall classification accuracy of this model on the test set is 0.179
The overall classification accuracy of the model can be calculated by dividing the number of correctly classified instances (the sum of true positives and true negatives) by the total number of instances in the test set
Accuracy = (TP + TN) / (TP + TN + FP + FN)
where TP = True Positives, TN = True Negatives, FP = False Positives, and FN = False Negatives.
From the confusion matrix given
True Positives (TP) = 124
True Negatives (TN) = 116
False Positives (FP) = 77
False Negatives (FN) = 851
Plugging these values into the formula, we get
Accuracy = (124 + 116) / (124 + 116 + 77 + 851)
Accuracy = 0.179
Learn more about confusion matrix here
brainly.com/question/29216338
#SPJ4
The given question is incomplete, the complete question is:
The following classification confusion matrix shows the results of a model's classifications on a test set: Test Set Results Model Prediction FALSE TRUE FALSE 116 TRUE 77 124 851 (The rows refer to the model's classifications, and the columns to the actual results in the test set.) a. What is the overall classification accuracy of this model on the test set?
g assuming the sample was randomly selected and the data is normally distributed, conduct a formal hypothesis test to determine if the population mean length of stay is significantly different from 6 days.
Answers
If the null hypothesis is rejected, we can conclude that there is evidence to suggest that the population mean length of stay is significantly different from 6 days.
If the null hypothesis is not rejected, we do not have sufficient evidence to conclude a significant difference.
What is Hypothesis?
A hypothesis is an assumption, an idea that is proposed for the purpose of argumentation so that it can be tested to see if it could be true. In the scientific method, a hypothesis is constructed before any applicable research is done, other than a basic background review.
To conduct a formal hypothesis test to determine if the population mean length of stay is significantly different from 6 days, we can set up the null and alternative hypotheses and perform a statistical test.
Null Hypothesis (H0): The population mean length of stay is equal to 6 days.
Alternative Hypothesis (H1): The population mean length of stay is significantly different from 6 days.
We can perform a t-test to compare the sample mean with the hypothesized population mean. Let's denote the sample mean as x and the sample standard deviation as s. We will use a significance level (α) of 0.05 for this test.
Collect a random sample of length of stay data. Let's assume the sample mean is x and the sample standard deviation is s.
Calculate the test statistic t-value using the formula:
t = (x - μ) / (s / √n)
Where μ is the hypothesized population mean (6 days), n is the sample size, x is the sample mean, and s is the sample standard deviation.
Determine the degrees of freedom (df) for the t-distribution. For a one-sample t-test, df = n - 1.
Find the critical t-value(s) based on the significance level and degrees of freedom. This can be done using a t-distribution table or a statistical software.
Compare the calculated t-value with the critical t-value(s). If the calculated t-value falls within the rejection region (i.e., outside the critical t-values), we reject the null hypothesis. Otherwise, we fail to reject the null hypothesis.
Calculate the p-value associated with the calculated t-value. The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed data, assuming the null hypothesis is true. If the p-value is less than the chosen significance level (α), we reject the null hypothesis.
Make a conclusion based on the results. If the null hypothesis is rejected, we can conclude that there is evidence to suggest that the population mean length of stay is significantly different from 6 days. If the null hypothesis is not rejected, we do not have sufficient evidence to conclude a significant difference.
To learn more about Hypothesis from the given link
https://brainly.com/question/606806
#SPJ4
A standing wave can be mathematically expressed as y(x,t) = Asin(kx)sin(wt)
A = max transverse displacement (amplitude), k = wave number, w = angular frequency, t = time.
At time t=0, what is the displacement of the string y(x,0)?
Express your answer in terms of A, k, and other introduced quantities.
Answers
The mathematical expression y(x,t) = Asin(kx)sin(wt) provides a way to describe the behavior of a standing wave in terms of its amplitude, frequency, and location along the string.
At time t=0,
the standing wave can be mathematically expressed as
y(x,0) = Asin(kx)sin(w*0) = Asin(kx)sin(0) = 0.
This means that the displacement of the string is zero at time t=0.
However, it is important to note that this does not mean that the string is not moving at all. Rather, it means that the string is in a state of equilibrium at time t=0, with the maximum transverse displacement being A.
As time progresses, the standing wave will oscillate between the maximum positive and negative transverse displacement values, creating a pattern of nodes (points of zero displacements) and antinodes (points of maximum displacement).
The wave number k and angular frequency w are both constants that are dependent on the physical properties of the string and the conditions under which the wave is being produced.
To learn more about Expression :
https://brainly.com/question/1859113
#SPJ11