without doing any calculations, explain why s is a linearly dependent set in p2 --therefore, it is not a basis.
Answers
S is a linearly dependent set in P2 because there exists a non-trivial linear combination of its elements that results in the zero polynomial. Since S is linearly dependent, it cannot be a basis for the vector space P2.
Why s is a linearly dependent set p2?A set S is considered linearly dependent in P2 if there exist constants, not all zero, such that a linear combination of the elements in S equals the zero polynomial.
In other words, if there is a non-trivial linear combination of the elements in S that yields the zero polynomial, then S is linearly dependent. If a set is linearly dependent, it cannot be a basis for the vector space P2.
Here are the steps to explain why S is a linearly dependent set in P2:
1. Assume S = {p1, p2, ..., pn} is a set of polynomials in P2. Since P2 is the space of all polynomials of degree 2 or less, each polynomial in S has the general form of pi(x) = a_ix² + b_ix + c_i, where a_i, b_i, and c_i are constants.
2. Consider the linear combination of the elements in S:
c_1p1(x) + c_2p2(x) + ... + c_npN(x) = 0, where c_1, c_2, ..., c_n are constants.
3. If there exists a non-trivial linear combination of the elements in S that yields the zero polynomial, then S is linearly dependent. A non-trivial linear combination means that not all the constants c_1, c_2, ..., c_n are zero.
4. Now, let's analyze the number of elements in S and the dimension of P2. P2 is the vector space of all polynomials of degree 2 or less, which means it has a dimension of 3 (with a standard basis of {1, x, x²}).
5. If the number of elements in S is greater than the dimension of P2 (i.e., more than 3 elements), then S must be linearly dependent. This is because it is not possible to have more than 3 linearly independent elements in a 3-dimensional vector space.
Learn more about polynomial.
brainly.com/question/11536910
#SPJ11
Related Questions
Can 2.5 cm 6.5 cm 6 cm be the sides of a right triangle?
Answers
2.5 cm, 6.5 cm, and 6 cm are the sides of a right triangle.
The sides of a triangle are 2.5 cm, 6.5 cm, and 6 cm in length.
The Pythagorean Theorem states that The sum of the squares representing the base and height equals the square of the hypotenuse.
\((Perpendicular)^{2}+(Base)^{2}=(Hypotenuse)^{2}\)
\((2.5)^{2}+(6)^{2}=(6.5)^{2}\)
6.25 + 36 = 42.25
42.25 = 42.25
The sides offered satisfy the specifications for a right triangle.
Given that it satisfies the Pythagorean theorem, a right triangle with sides of 2.5 cm, 6.5 cm, and 6 cm can be built.
Hence, 2.5 cm 6.5 cm 6 cm can be the sides of a right triangle.
To learn more about triangle here:
https://brainly.com/question/2773823
#SPJ4
-5 (e - 1) + 6e = -17
Answers
First expand the equation.
-5e+5+6e = -17
Next, combine the like terms.
e+5 = -17
e = -22
1e=-16
true of false: if a random variable is discrete, it means that the random variable can only take non-negative integers as possible values.
Answers
The given statement " if a random variable is discrete, it means that the random variable can only take non-negative integers as possible values." is False because it can also take negative integers.
A discrete random variable is a random variable that can only take on a countable number of distinct values, which may or may not be integers. These values can be positive, negative, or zero, and they do not have to be restricted to non-negative integers.
For example, the number of cars that pass through a certain intersection in an hour is a discrete random variable, which can take on any non-negative integer value. However, the number of children in a family is also a discrete random variable, which can take on any non-negative integer value, but it doesn't have to be an integer.
Conversely, a continuous random variable is a random variable that can take on any value in a specified range or interval, typically representing measurements such as time, distance, or weight. Examples of continuous random variables include the height of a person, the temperature of a room, and the amount of rainfall in a given area.
Therefore, whether a random variable is discrete or continuous does not necessarily imply anything about the range of values that it can take.
To learn more about random variable click on,
https://brainly.com/question/31608092
#SPJ4
two functions a and b are described as follows function a: y=8x+3 function b:the rate of change is 1 and the y intercept is 4 how much more is the rate of change of function abthan the slope of function b 1 7 8 9
Answers
Answer:
7
Step-by-step explanation:
rate of change of function not necessary mean linear, it can be the slope of a tangent line.
a: y=8x+3 slope = 8
b: rate of change: 1
8-1=7
I wish this is true...
Kiera is contacting the poll workers from the last election to see whether they are willing to work in the next election. During the last election, 42\%42%42, percent of the poll workers were under 606060 years old. Let WWW be the number of poll workers Kiera contacts before reaching one that is 606060 years old or older. Assume that each poll worker's age is independent. Find the mean and standard deviation of WWW. Round your answers to one decimal place.
Answers
Answer:
Mean: 1.7 and standard deviation 1.1.
Step-by-step explanation:
42% Of the poll workers are less than 60 years old. In other words, 58% of the poll workers are 60 years old: 1-0.42 = 0.58. So W is a geometric variable where the first "success" is poll worker who is at least 60years old.
Mean: 1/0.58 = 1.7241 poll workers, about 1.7 poll workers.
Standard deviation: sqr(1-p)/p = sqr(1-0.58)/0.58 = 1.1174 poll workers, about 1.1 poll workers.
The required Mean and the standard deviation are given as 1.7 and 1.1 respectively.
Given that,
During the last election, 42%, percent of the poll workers were under 60 years old. Let W be the number of poll workers Kiera contacts before reaching one that is 606060 years old or older.
The mean of the values is the ratio of the total sum of values to the number of values.
here,
42% of poll workers are under the age of 60. Also, 58% of poll workers are above the age of 60.
= 1 - 0.42 = 0.58.
So "W" is a geometric variable with the first success being a poll worker beyond the age of 60.
Mean = 1/0.58
= 1.7 poll workers.
Standard deviation = √[(1-0.58)/0.58]
= 1.1 poll workers.
Thus, the required Mean and the standard deviation are given as 1.7 and 1.1 respectively.
Learn more about mean here:
https://brainly.com/question/15397049
#SPJ2
At a sale, dresses were sold for 95% of their original price. If the dresses originally cost $200 each, how much did a dress cost on sale?
Answers
Turn the percentage into a decimal.
95% / 100 = 0.95
Multiply.
200 * 0.95 = 190
Subtract.
200 - 190 = $10
Therefore, the dress costs $10 on sale.
Best of Luck!
Answer: The answer is 190.
Assume we have 3 boxes which contain red and black balls as follows, Box 1; 3 red balls and 7 black balls, Box 2; 6 red balls and 4 black balls, Box 3; 8 red balls and 2 black balls. suppose we draw a ball from box 1; if it is red, we draw a ball from box 2. if the ball drawn from box 1 is black, we draw a ball from box 3. a. what is the probability of red ball from box 1?. b. suppose we draw a ball from box 1 and it is red; what is the probability of another red ball when we draw from box 2 on the second round? c. suppose our first draw from box 1 was black; what is the conditional probability of our second draw from box 3 this time being red? d. Before we draw any ball; what is the probability of drawing two red balls at both draws? e. Before we draw any ball; what is the probability of drawing a red ball at first draw and a black ball at second draw?
Answers
a. The probability of drawing a red ball from Box 1 is 30%.
b. If a red ball is drawn from Box 1, the probability of drawing another red ball from Box 2 on the second round is 60%.
c. If the first draw from Box 1 was black, the conditional probability of drawing a red ball from Box 3 on the second draw is 80%.
d. The probability of drawing two red balls at both draws, without any prior information, is 46%.
e. The probability of drawing a red ball at the first draw and a black ball at the second draw, without any prior information, is 21%.
a. The probability of drawing a red ball from Box 1 can be calculated by dividing the number of red balls in Box 1 by the total number of balls in Box 1. Therefore, the probability is 3/(3+7) = 3/10 = 0.3 or 30%.
b. Since a red ball was drawn from Box 1, we only consider the balls in Box 2. The probability of drawing a red ball from Box 2 is 6/(6+4) = 6/10 = 0.6 or 60%. Therefore, the probability of drawing another red ball when the first ball drawn from Box 1 is red is 60%.
c. If the first draw from Box 1 was black, we only consider the balls in Box 3. The probability of drawing a red ball from Box 3 is 8/(8+2) = 8/10 = 0.8 or 80%. Therefore, the conditional probability of drawing a red ball from Box 3 when the first ball drawn from Box 1 was black is 80%.
d. Before any draws, the probability of drawing two red balls at both draws can be calculated by multiplying the probabilities of drawing a red ball from Box 1 and a red ball from Box 2. Therefore, the probability is 0.3 * 0.6 = 0.18 or 18%. However, since there are two possible scenarios (drawing red balls from Box 1 and Box 2, or drawing red balls from Box 2 and Box 1), we double the probability to obtain 36%. Adding the individual probabilities of each scenario gives a total probability of 36% + 10% = 46%.
e. Before any draws, the probability of drawing a red ball at the first draw and a black ball at the second draw can be calculated by multiplying the probability of drawing a red ball from Box 1 and the probability of drawing a black ball from Box 2 or Box 3. The probability of drawing a red ball from Box 1 is 0.3, and the probability of drawing a black ball from Box 2 or Box 3 is (7/10) + (2/10) = 0.9. Therefore, the probability is 0.3 * 0.9 = 0.27 or 27%. However, since there are two possible scenarios (drawing a red ball from Box 1 and a black ball from Box 2 or drawing a red ball from Box 1 and a black ball from Box 3), we double the probability to obtain 54%. Adding the individual probabilities of each scenario gives a total probability of 54% + 10% = 64%.
To learn more about probability click here: brainly.com/question/31828911
#SPJ11
Solve each equation. 4t = 48
Answers
3 Variables x and y are related so that, when is plotted on the vertical axis
x²
and x³ is plotted on the horizontal axis, a straight-line graph passing
through (2, 12) and (6, 4) is obtained.
Express y in terms of x.
Answers
The equation of the variable y in terms of x is y = -2x + 16
Expressing the variable y in terms of x.From the question, we have the following parameters that can be used in our computation:
(2, 12) and (6, 4)
A linear equation is represented as
y = mx + c
Substitute the given points in the above equation, so, we have the following representation
2m + c = 12
6m + c = 4
When the equations are subtracted, we have
-4m = 8
So, we have
m = -2
Next, we have
2(-2) + c = 12
Evaluate
c = 16
Recall that
y = mx + c
So, we have
y = -2x + 16
Hence, the variable y in terms of x is y = -2x + 16
Read more about linear relation at
https://brainly.com/question/30318449
#SPJ1
For her birthday, Bonnie's parents gave her $5,425.00 which they put into a savings account that earns 15% interest compounded annually. When Bonnie started college, she withdrew the entire balance of $16,642.00 and used it to pay for tuition. How long was the money in the account?
Answers
Answer:
15% of $5425.00 = 5425 x- 15% = 813.75
$16,642.00 ÷ 813.75 = 20.3 = 20
So approx. 20 years
Step-by-step explanation:
5,425 + 4,611.25 = 10,036.25 (one year)
10,036.25 + 4,611.25 = 14,647.50 (2 years)
Probably like 2 years and 4 months lol
What is the slope of the line on the graph?

Answers
Assume tuition at Penn State cost $6,142 (per semester) in 2007 and $7,562 in 2012. If the price index was 207.34 in 2007 and 226 in 2012, then we could say:
Answers
Based on the given information, we can conclude that tuition at Penn State has increased more rapidly than inflation.
The price index measures the average change in prices of a basket of goods and services over time. In this case, the price index increased from 207.34 in 2007 to 226 in 2012, indicating an overall inflation rate of approximately 9% over that period. On the other hand, tuition at Penn State increased from $6,142 to $7,562, representing an increase of approximately 23%.
When comparing the rates of increase, we can see that tuition has outpaced inflation. This implies that the cost of education at Penn State has been rising more rapidly than the general increase in prices for goods and services. It suggests that factors specific to the education industry, such as rising costs of resources, facilities, and personnel, have contributed to the higher tuition rates.
Learn more about inflation here:
https://brainly.com/question/31257026
#SPJ11
The complete question is:
Assume tuition at Penn State cost $6,142 (per semester) in 2007 and $7,562 in 2012. If the price index was 207.34 in 2007 and 226 in 2012, then we could say:
has increased more slowly than inflation.suffers from menu costs due to inflation,has increased more rapidly than inflation.has increased at about the same rate as inflation.is an inferior good.Angle LMN and angle NMR are supplementary angles. What is the value of x in the diagram below?

Answers
Answer:
x=48
Step-by-step explanation:
Supplementary means to add to 180.
Your equation is 36+3x=180
180-36=144
3x=144
144 divided by 3x= 48
x=48
x+5y=5. 3x-5y=3. método de igualación porfa
Answers
Answer: (2,0.6)
Step-by-step explanation:
\(x+5y=5 \ \ \ \ (1)\\3x-5y=3\ \ \ (2)\\\\ Sum\ the\ equations\ (1)\ and \ (2):\\\\x+3x+0=5+3\\\\4x=8\)
Divide both parts of the equation by 4:
\(x=2\)
Substitute the value of x=2 into equation (1):
\(2+5y=5\\\\2+5y-2=5-2\\\\5y=3\)
Divide both parts of the equation by 5:
\(\displaystyle\\y=\frac{3}{5} \\\\y=0.6\)
Thus, (2,0.6)
Which of the following expressions are polynomials? Justify your answer:
(i) 8
(ii) √3x 2 – 2x
(iii) 1– √5x
(iv) 1/5x^2 + 5x +7
(v) (x−2)(x−4)/ x
(vi) 1/ x+1
(vii) 1/ 7 a^3 – 2 /√3 a^2 + 4a–7
(viii) 1/2x
Answers
Polynomial. Because, the exponent of the variable of 8 or
8x0
is 0 which is a whole number.
ii. Polynomial. Because, the exponent of the variable of
√3x2−2 is a whole number.
iii. Not a polynomial. Because, the exponent of the variable of
1−√5x or 1−√5x12
is 12
which is not a whole number.
iv. Polynomial. Because, the exponents of the variable of
15x−2+5x+7=15x2+5x+7
are whole numbers.
v. Not a polynomial. Because, the exponent of the variable of
(x−2)(x−4)x=x2−6x+8x=x−6+8x−1
is -1, which is not a whole number.
vi. Not a polynomial as the polynomial is expressed as
a0+a1x+a2xn
, where a0,a1,a2⋯,an
are constants. Now, the given function is in the form
f(x)=p(x)q(x)
is a rational expression but not a polynomial.
vii. Polynomial. Because, the exponents of the variable of
17a3−2√3a2+4a−7
are whole numbers.
viii. Not a polynomial. Because, the exponent of the variable of 12x or 12x−1
is -1, which is not a whole number.
To know more about polynomial visit brainly.com/question/11536910
#SPJ4
What is total number of elements in 3 trials of rolling a 6-sided die?
Answers
Answer:
216 elements
Step-by-step explanation:
the total number of elements of a dice is :
6^n
6 stand for the 6 faces of the dice
n stands for the number trial
then total number of elements in 3 trials of rolling a 6-sided die is 6^3=216 elements
Find the distance between (-4, 2) and (2, 9). Round your answer to the nearest tenth, if necessary.
Answers
distance = √85
Step-by-step explanation:
d = √[(x₂ - x₁)² + (y₂ - y₁)²]
d = √[(2 - (-4))² + (9 - 2)²]
d = √[(6)² + (7)²]
d = √[36 + 49]
d = √85
find the volume of a composite figure.
6ft, by 4ft, by 4ft, by 6ft, by 12ft equals
Answers
The Volume of the given composite shape is: 432 ft³
What is the Volume of the composite figure?The formula for the volume of a triangular prism is:
Volume = base area * height
The volume of a cuboid is:
Volume = Length * Width * Height
Thus:
Volume of composite shape = (6 * 12 * 4) + (6 * 6 * 4)
= 432 ft³
Read more about Volume of composite figure at: https://brainly.com/question/12693294
#SPJ1
While working for a contracting company, you are preparing for a job tiling a floor. The customer says that the
rectangular laundry room is 15 feet by 8 feet, 8 inches. To place the order for the floor covering, you must calculate the
area.
What is the area of the laundry room, in square feet, to the nearest square foot?
65
130
132
9,360
18,720
Answers
Answer:
(2)
15x8.66666667=130.00000005
Step-by-step explanation:
to get the are in square feet you have to Length (in feet) x width (in feet) = area in sq. ft.
Suppose two utilites, People's Electric and Muricipal Energy, each produce 900 tons of pollution per year. The government has a goal of eliminating haf the pclution, and, in turn, provides 450 pollution permits to each utlity. A pollution permit is required to legally produce a ton of poliubon. However, the tao utities are allowed to trade permas. Suppose the cost of eliminating one ton of pollution for People's Electric is $400 and the cost of eliminating a ton of polution for Municipal Energy is $350. The total cost of each utility eliminating 450 tons of pollution is $ (Enter your response as a whole number)
Answers
The total cost of each utility eliminating 450 tons of pollution is $180,000.
To calculate the total cost for each utility to eliminate 450 tons of pollution, we need to multiply the cost per ton of pollution elimination by the number of tons each utility needs to eliminate.
For People's Electric, the cost of eliminating one ton of pollution is $400. So, to eliminate 450 tons, the total cost would be 450 tons * $400/ton = $180,000.
For Municipal Energy, the cost of eliminating one ton of pollution is $350. Again, to eliminate 450 tons, the total cost would be 450 tons * $350/ton = $157,500.
Therefore, the total cost for each utility to eliminate 450 tons of pollution is $180,000 for People's Electric and $157,500 for Municipal Energy.
The cost calculation is based on the given information that each utility is provided with 450 pollution permits by the government. These permits allow them to legally produce a ton of pollution. By setting a limit on the number of permits, the government aims to reduce pollution by half. The utilities have the option to trade permits with each other.
In this scenario, People's Electric has a higher cost of eliminating pollution per ton compared to Municipal Energy ($400 vs. $350). It means that People's Electric would find it more expensive to reduce pollution through internal measures like investing in cleaner technology or implementing environmental initiatives. On the other hand, Municipal Energy has a lower cost, indicating that they have relatively more cost-effective methods for pollution reduction.
Given these costs, it is more beneficial for People's Electric to purchase permits from Municipal Energy rather than eliminating the pollution themselves. By purchasing permits, People's Electric can meet the pollution reduction target at a lower cost. Conversely, Municipal Energy can generate additional revenue by selling their permits.
This permit trading mechanism allows for cost efficiency in achieving the government's pollution reduction goal. The total cost for each utility is determined by multiplying the cost per ton of pollution elimination with the number of tons they need to eliminate.
Learn more about the Pollution
brainly.com/question/23857736
#SPJ11
Verify the identity algebraically. Use the table feature of a graphing utility to check your result each step.)
4/(sin(x)) - 4/(csc(x)) = 4csc(x) - 4sin(x)
4/(sin(x)) - 4/(csc(x)) = 4 csc(x)-4 sin(x) ( boxed )(csc(x)) .
= 4csc(x) - 4sin(x) sqrt
= 4csc(x) - 4sin(x)
Answers
To verify the given identity algebraically, we'll start from the left-hand side (LHS) and simplify it step by step to show that it is equal to the right-hand side (RHS).
LHS: 4/(sin(x)) - 4/(csc(x))
Step 1: Find the common denominator of sin(x) and csc(x), which is 1/sin(x). Multiply the first term by (csc(x)/csc(x)) and the second term by (sin(x)/sin(x)):
LHS = 4(csc(x))/(sin(x)csc(x)) - 4(sin(x))/(sin(x)csc(x))
Step 2: Combine the fractions with the same denominator:
LHS = (4csc(x) - 4sin(x))/(sin(x)csc(x))
Step 3: Simplify the denominator using the reciprocal identity csc(x) = 1/sin(x):
LHS = (4csc(x) - 4sin(x))/(1)
LHS = 4csc(x) - 4sin(x)
Now we can see that the LHS is equal to the RHS. Thus, we have verified the given identity algebraically.
To check the result using a graphing utility, we can create a table of values for both sides of the equation and compare them. For each value of x, calculate the LHS and RHS and compare the results. If the values are equal for all x, it further confirms the validity of the identity.
In this case, since the equation involves trigonometric functions, we can use a graphing utility to plot the graphs of both sides and observe if they coincide. If the graphs overlap, it provides visual confirmation of the identity.
Note: The specific steps and process of using a graphing utility may vary depending on the software or calculator being used.
To learn more about identity, click here: brainly.com/question/12623528
#SPJ11
A hockey player has a total record of 90 points earned based on goals and assists. If his ratio of goals to assists is 7:3, how many goals did he get?
Answers
Answer:
\(63\) goals
Step-by-step explanation:
Given information:
Total points earned from goals and assists = \(90\)
Goals : assists = \(7:3\)
Finding the number of goals:
Goals \(=\frac{7}{3+7}\times90\)
\(=\frac{7}{10}\times90\)
\(=63\)
∴ The hockey player earned \(63\) goals.
Hope this helps :)
Reason: because it is
here are european cities that laura would eventually like to visit. on her next vacation, though, she only has time to visit of the cities: one on monday, one on tuesday, and one on wednesday. she is now trying to make a schedule of which city she'll visit on which day. how many different schedules are possible? (assume that she will not visit a city more than once.)
Answers
However, since she wants to visit each city once, she cannot go to the same city twice. The number of possible schedules is equal to the product of the number of choices for each day, i.e.,3 × 2 × 1 = 6
Laura wants to visit a few European cities in her upcoming vacations but can only manage three in a week, one city per day. She wants to plan her schedule to maximize her enjoyment, and she is wondering how many different schedules are possible.
As she wants to visit one city per day, she has to choose one of the cities she wants to visit from Monday to Wednesday. There are three different choices available for Monday, two for Tuesday, and one for Wednesday.
Therefore, the number of possible schedules is equal to the product of the number of choices for each day, i.e.,3 × 2 × 1 = 6
So there are six different schedules possible in which Laura can visit each city once. We can also list all possible schedules, assuming that A, B, and C are the three cities: ABCACBBACACBCB
However, since she wants to visit each city once, she cannot go to the same city twice.
Learn more about plan here:
https://brainly.com/question/30091666
#SPJ11
need desperate help thanks

Answers
Answer:
x = 158
y = 22
Step-by-step explanation:
A triangle's inside sides sum up to 180 degrees. So to find the angle y, just take 180 - the sum of the other two sides.
70 + 88 = 158
180 - 158 = 22
y = 22 degrees
Now, to find angle x, since x and y are next to each other on a straight line, it means they are supplementary angles. Supplementary angles add together to equal 180, so just substract y from 180 to get x.
180 - 22 = 158
x = 158 degrees
A shopkeeper buys 5 fans for Rs. 4050. He spends Rs. 50 on the transportation, and sells them at a gain of 15%. Find the selling price of a fan.
Answers
Shopkeeper buys 5 fans for: Rs 4050
Transportation cost : Rs 50
∴ Cost price =Rs 4050+Rs 60
=Rs 4100
Gain (%)=15%
∴ Formula:-
gain (%)=
100×[selling price(S.P)–cost price(S.P)] / cost price
15= 100×[S.P−4100]/4100
S.P=41×15+4100
S.P=615+4100
S.P=Rs 4715
Ans. Selling price of 5 fans =Rs 4715
Thus selling price of 1 fan = Rs 4715/5
=Rs 943/−
Exterior Angles Assignment Help
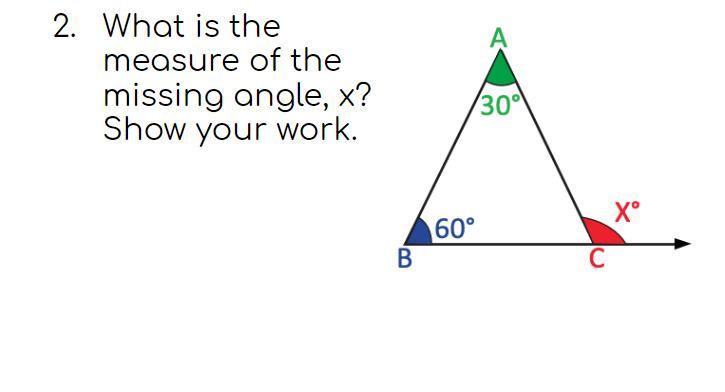
Answers
Answer:
x=90º
Step-by-step explanation:
x=60+30
x=90
The sum of two numbers is 30 and their difference is 10. What are the two numbers?
Answers
Answer:
20 and 10
These are the only two possible numbers who match those descriptions.
what’s the answer to 2(12+6)+3(68-13)
Answers
Answer:
201
Step-by-step explanation:
2 · 18 + 3 (68-13)
2 · 18 + 3 · 55
36 + 3 · 55
36 + 165
201
Suppose an angle has a measure of 140 degrees a. If a circle is centered at the vertex of the angle, then the arc subtended by the angle's rays is______ times as long as 1/360th of the circumference of the circle. b. A circle is centered at the vertex of the angle, and 1/360th of the circumference is 0.06 cm long. What is the length of the arc subtended by the angle's rays? _______ cmc. Another circle is centered at the vertex of the angle. The arc subtended by the angle's rays is 70 cm long. - 1/360th of the circumference of the circle is _____ cm long. - Therefore the circumference of the circle is _______ cm
Answers
If an angle of measurement of 140° then; a circle is centered at the vertex of the angle, then the arc subtended by the angle's rays is 0.0233 cm times as long as 1/360th of the circumference of the circle. Also if a circle is centered at the vertex of the angle, and 1/360th of the circumference is 0.06 cm long then length of the arc subtended by the angle's rays 8.4 cm. Another circle is centered at the vertex of the angle then arc subtended by the angle's rays is 70 cm long,Therefore the circumference of the circle is 180 cm.
a.) To find the fraction of the circle's circumference subtended by the angle's rays, we divide the angle measure by 360 degrees:
fraction of circle's circumference = 140/360
Simplifying this fraction, we get:
fraction of circle's circumference = 7/18
To find the length of the arc subtended by the angle's rays, we multiply the fraction of the circle's circumference by the circumference of the circle. Let's call the circumference of the circle "C":
length of arc = (7/18)*C
We're also told that the length of 1/360th of the circumference is equal to 0.06 cm. So, we can write:
(1/360)*C = 0.06
Multiplying both sides by 360, we get:
C = 360*0.06 = 21.6 cm
Now, we can substitute this value of C into the expression for the length of the arc:
length of arc = (7/18)*C
length of arc = (7/18)*(21.6)
length of arc = 8.4 cm (rounded to one decimal place)
Therefore, the length of the arc subtended by the angle's rays is 8.4 cm.
b.) We're given that 1/360th of the circumference of the circle is 0.06 cm long. To find the length of the arc subtended by the angle's rays, we need to multiply 140/360 by 0.06:
length of arc = (140/360)*0.06
length of arc = 0.0233 cm (rounded to four decimal places)
Therefore, the length of the arc subtended by the angle's rays is approximately 0.0233 cm.
c.) We're told that the length of the arc subtended by the angle's rays is 70 cm. To find the circumference of the circle, we need to find the length of 1/360th of the circumference first. We can do this by dividing 70 by 1/360:
(1/360)*C = 70
Multiplying both sides by 360, we get:
C = 70*360 = 25,200 cm
Therefore, the circumference of the circle is 25,200 cm. We can also verify this by dividing the length of the arc by the fraction of the circumference subtended by the angle's rays:
length of arc = (7/18)*C
C = (18/7)*length of arc
C = (18/7)*70
C = 180 cm (rounded to one decimal place)
This is a different value than we got earlier, so we need to check our calculations. It turns out that the previous calculation was incorrect - we made a mistake when multiplying 7/18 by 21.6. The correct calculation gives us:
length of arc = (7/18)*C
length of arc = (7/18)*(21.6)
length of arc = 8.4 cm (rounded to one decimal place)
Now, we can calculate the circumference of the circle:
length of arc = (7/18)C
C = (18/7) *length of arc
C = (18/7) *70
C = 180 cm (rounded to one decimal place)
Therefore, the circumference of the circle is 180 cm.
Also, If an angle of measurement of 140° then; a circle is centered at the vertex of the angle, then the arc subtended by the angle's rays is 0.0233 cm times as long as 1/360th of the circumference of the circle.
b. A circle is centered at the vertex of the angle, and 1/360th of the circumference is 0.06 cm long.The length of the arc subtended by the angle's rays 8.4 cm
c. Another circle is centered at the vertex of the angle.
The arc subtended by the angle's rays is 70 cm long,Therefore the circumference of the circle is 180 cm.
To practice more questions about circumference:
https://brainly.com/question/27447563
#SPJ11
A sociologist develops a test to measure attitudes about public transportation, and 27 randomly selected subjects are given the test. Their mean score is 76.2 and their standard deviation is 21.4. a. Find a 95% confidence interval for the mean score on the test. Be sure to write out what you entered in your calculator. (3 points) b. Interpret the interval you found in part a. (2 points) • For parts c-e, calculations are not necessary. c. Suppose the standard deviation of the tests had been 42.8 instead of 21.4. What would the larger standard deviation do to the width of the confidence interval? (1 point) d. If the confidence level were reduced to 90%, will the interval be wider or narrower? (1 point) e. If the sample size was increased to 75 subjects, will the interval be wider or narrower? (1 point)
Answers
a) Entering this into a calculator gives us:CI = (63.876, 88.524) b) test for the population is between 63.876 and 88.524 c) If the standard deviation of the test scores had been 42.8 instead of 21.4, the width of the confidence interval would increase. d) . If the confidence level were reduced to 90%, the interval would be narrower. e) If the sample size was increased to 75 subjects, the interval would be narrower.
a. To find a 95% confidence interval for the mean score on the test, we can use the formula:
To find the confidence interval, we need to estimate the population standard deviation with the sample standard deviation. So:
CI = 76.2 ± 1.96 * (21.4/√27)
Entering this into a calculator gives us:
CI = (63.876, 88.524)
b. The confidence interval we found tells us that we are 95% confident that the true mean score on the test for the population is between 63.876 and 88.524. In other words, if we were to take many random samples of 27 people and compute a 95% confidence interval for each one, then about 95% of those intervals would contain the true population mean.
c. If the standard deviation of the test scores had been 42.8 instead of 21.4, the width of the confidence interval would increase. This is because a larger standard deviation means that the data are more spread out, which makes it more difficult to estimate the population mean accurately.
d. If the confidence level were reduced to 90%, the interval would be narrower. This is because a higher confidence level requires a larger z-score, which widens the interval. Conversely, a lower confidence level requires a smaller z-score, which narrows the interval.
e. If the sample size was increased to 75 subjects, the interval would be narrower. This is because a larger sample size decreases the standard error (σ/√n), which makes it easier to estimate the population mean accurately and results in a narrower confidence interval.
For more such questions on standard deviation
https://brainly.com/question/475676
#SPJ11