why mathematics is indispensible
Answers
Related Questions
An employee at a company is paid based on years of experience and years of education. Write the equation for their salary.
Salary, S, is 35,000 plus the product of 2,000 and years of experience, X, plus the product of 3,000 and years of education, D.
S=35,000x+2,000D
S=2,000x+3,000D
S=35,000+2,000x+3,000D
S+35,000=2,000x+3,000D
Answers
The compensation equation for the employee may be stated as follows:
\(\text{S}=35000+2000\text{x}+3000\text{D}\)What is a equation?A equation is a mathematical statement that claims the equivalence of two expressions. Equations are used in mathematics, science, engineering, and many other professions to express connections between variables and to solve problems.
If s denotes income, x denotes years of experience, and d denotes years of education.
The employee's remuneration is computed as the basic wage of $35,000 + $2,000 for each year of experience plus $3,000 for each year of study. In deciding an employee's wage, this equation considers both their experience and education.
Therefore, \(\text{S}=35000+2000\text{x}+3000\text{D}\) is the compensation equation for the employee.
To know more on equations, please refer to the link below:
https://brainly.com/question/29538993
Evaluate the expression for s = 10, t = –2, and u = 9.
t2u + s = ?
Answers
Answer:
46
Step-by-step explanation:
You want to evaluate the expression t²u+s for t=-2, u=9, s=10.
Evaluating an expressionPut the numbers in the places of the corresponding variables, and do the arithmetic.
(-2)²·9 +10 = 4·9 +10 = 36 +10 = 46
The value of the expression is 46.

Real-life Problems Question 10

Answers
Answer :
a) It is given that
Everyday a machine makes 500000 staples and puts them into the boxes.
The machine need 170 staples to fill a box
One box contans = 170 staples.
Total number of staples = 500000
Number of box required to fill 500000 staples = Total number of staples/No. of staples 1 box contains.
\( \: :\implies \) 500000 /170
\( :\implies \: \) 2941 (approx)
Therefore, 2941 boxes are required to fill with 500000 staples.
b) It is given that,
Each staple is made of 0.21 g of metal .
Total weight of metal = 1 kg = 1000 g
1 staple = 0.21 g
Number of staples = weight of metal/ Weight of 1 staple.
\( \: :\implies \) 1000/0.21
\( \: :\implies \) 4761 (approximately)
Therefore, 4761 staples can be made from 1 kg of the metal.
Determine the measure of x in the diagram below:
x = °

Answers
The measure of angle x on the straight line is 130 degrees.
What is the measure of angle x?The sum of interior angles in a triangle equals 180 degrees.
To determine the value of x, we first determine its suplemetary angle x .
Hence:
40 + 90 + ( suplemetary angle of x ) = 180
Solve for the suplementary angle:
130 + ( suplemetary angle of x ) = 180
Suplementary angle of x = 180 - 130
Suplemetary angle of x = 50 degree
Now, we can find the measure of angle x.
Note that, sum of angles on a straight line equals 180 degree.
Hence:
x + ( suplemetary angle of x ) = 180
x + 50 = 180
Solve for x
x = 180 - 50
x = 130 degrees.
Therefore, the value of x is 130 degrees.
Learn about area of triangle here: brainly.com/question/29156501
#SPJ1
Which point is a good approximation of a turning point
of the graph?
0 (-1.5,3)
0 (-0.5, -1)
0 (0,0)
O (1.0)

Answers
Answer:
(-0.5, -1)
Step-by-step explanation:
A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising)
Tim can restock the store in 9 hours. If Keith helps, it takes them
8 hours. Without help, how long would it take Keith to finish this job?
Answers
Answer:
um i think 8 not really but its maybe 8 or 17 not really sure
If I can prove that X is c.e. and ω∖X is c.e. then I can prove that X is computable by the theorem "Let W⊆ω. Then W is computable if both W and ω∖W are c.e". But I'm not able to proceed on how should I do this.
Answers
Proving X is computable by the theorem "Let W⊆ω. Then W is computable if both W and ω∖W are c.e".
Given :
If I can prove that X is c.e. and ω∖X is c.e. then I can prove that X is computable by the theorem "Let W⊆ω. Then W is computable if both W and ω∖W are c.e". But I'm not able to proceed on how should I do this.
Take a computable surjection :
f : ω → W.
Defined G = { f ( x ) ∣ x ∈ ω and ∀y < x ( f ( y ) < f ( x ) ) }.
here clearly, G ⊆ W .
And G is infinite. For if f ( x ) ∈ G, take the smallest y such that f ( y ) > f ( x ); then f ( y ) ∈ V.
Learn more about the theorem here:
https://brainly.com/question/12642646
#SPJ4
Could someone help me solve this? TIA

Answers
The exact value of the specified trigonometric identity found using the the trigonometric identity for tan(A - B) and tan(arccos(x)) and tanarcsin(x)) is presented as follows;
\(tan\left(sin^{-1}\left(\dfrac{3}{4} \right) - cos^{-1}\left(\dfrac{1}{5}\right) \right) =\dfrac{32\cdot \sqrt{6}- 75\cdot \sqrt{7} }{209}\)
What is a trigonometric identity?A trigonometric identity is an equality that involves trigonometric functions that is valid for all values of the arguments of the equation
The required trigonometric identities are;
\(tan (A - B) = \dfrac{tan(A) -tan(B)}{1-tan(A)\cdot tan(B)}\)
\(tan(sin^{-1}(x)) = \dfrac{x}{\sqrt{1-x^2} }\)
\(tan(cos^{-1}(x)) = \dfrac{\sqrt{1-x^2}}{x }\)
Therefore;
\(tan\left(sin^{-1}\left(\dfrac{3}{4} \right) - cos^{-1}\left(\dfrac{1}{5}\right) \right) = \dfrac{tan\left(sin^{-1}\left(\dfrac{3}{4} \right)\right)-tan\left(cos^{-1}\left(\dfrac{1}{5} \right)\right)}{1-tan\left(sin^{-1}\left(\dfrac{3}{4} \right)\right)\times tan\left(cos^{-1}\left(\dfrac{1}{5} \right)\right)}\)
Which gives;
\(\dfrac{\dfrac{\frac{3}{4} }{\sqrt{1-\left(\frac{3}{4} \right)^2} } -\dfrac{\sqrt{1-\left(\frac{1}{5} \right)^2}}{\frac{1}{5} } }{1+\dfrac{\frac{3}{4} }{\sqrt{1-\left(\frac{3}{4} \right)^2} } \times \dfrac{\sqrt{1-\left(\frac{1}{5} \right)^2}}{\frac{1}{5} }}=\dfrac{\dfrac{3\cdot \sqrt{7}-14\cdot \sqrt{6} }{7} }{\dfrac{7+6\cdot \sqrt{42} }{7} }\)
\(\dfrac{\dfrac{3\cdot \sqrt{7}-14\cdot \sqrt{6} }{7} }{\dfrac{7+6\cdot \sqrt{42} }{7} }=\dfrac{32\cdot \sqrt{6}- 75\cdot \sqrt{7} }{209}\)
Which indicates that we have;
\(tan\left(sin^{-1}\left(\dfrac{3}{4} \right) - cos^{-1}\left(\dfrac{1}{5}\right) \right) =\dfrac{32\cdot \sqrt{6}- 75\cdot \sqrt{7} }{209}\)
Learn more about trigonometric identity here:
https://brainly.com/question/24496175
#SPJ1
HELP PLEASE I REALLY NEED HELP ON THIS QUESTION HELP!

Answers
The number for which the theoretical probability matches the experimental probability is 2.
What is experimental and theoretical probability?
Experimental probability and theoretical probability are two different ways to determine the likelihood of an event occurring.
Experimental probability is determined by performing an experiment or conducting observations and collecting data to see how often an event occurs. This method involves counting the number of times an event occurs and dividing that number by the total number of trials or observations.
Theoretical probability, on the other hand, is determined by using mathematical principles and calculations to determine the likelihood of an event occurring. It is based on the assumption that all outcomes are equally likely.
In the given table;
For theoretical, P(2) = 1/4
For experimental, P(7) = 7/28 = 1/4
Learn more about experimental probability here: https://brainly.com/question/8652467
#SPJ1
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
Question 27, pre calc, please be quick, it is one am for me and I have exams tomorrow, include answer in bold.

Answers
To determine the type of discontinuity that exists at f(20):
According to the graph,
There is no discontinuity that exists at f(20).
Hence, the correct option is the first one.
help so i cna get out of class

Answers
Based on the given conditions, the lock solution is 205.
How to solve a lock?To solve the lock, to calculate the total score based on the given conditions:
Crocus: + 20
Daffodil: + 25
Snowflake: - 50
Tulip: + 30
Bird-Red: + 25, else + 10
Calculating the scores for each input:
TULIP: +30
CROCUS: +20
DAFFODIL: +25
TULIP: +30
DAFFODIL: +25
TULIP: +30
DAFFODIL: +25
CROCUS: +20
Total score = 30 + 20 + 25 + 30 + 25 + 30 + 25 + 20 = 205
Therefore, the solution for the lock is 205.
Find out more on lock solution here: https://brainly.com/question/19191108
#SPJ1
Image transcribed:
SPRING NOW LOADING.
<IF CROCUS, THEN +20>
<IF DAFFODIL, THEN +25>
<IF SNOWFLAKE, THEN -50>
<IF TULIP, THEN +30>
<IF BIRD-RED, THEN +25, ELSE + 10>
TULIP
CROCUS
DAFFODIL
TULIP
DAFFODIL
TULIP
DAFFODIL
CROCUS
Solve Lock
Help is my work right?
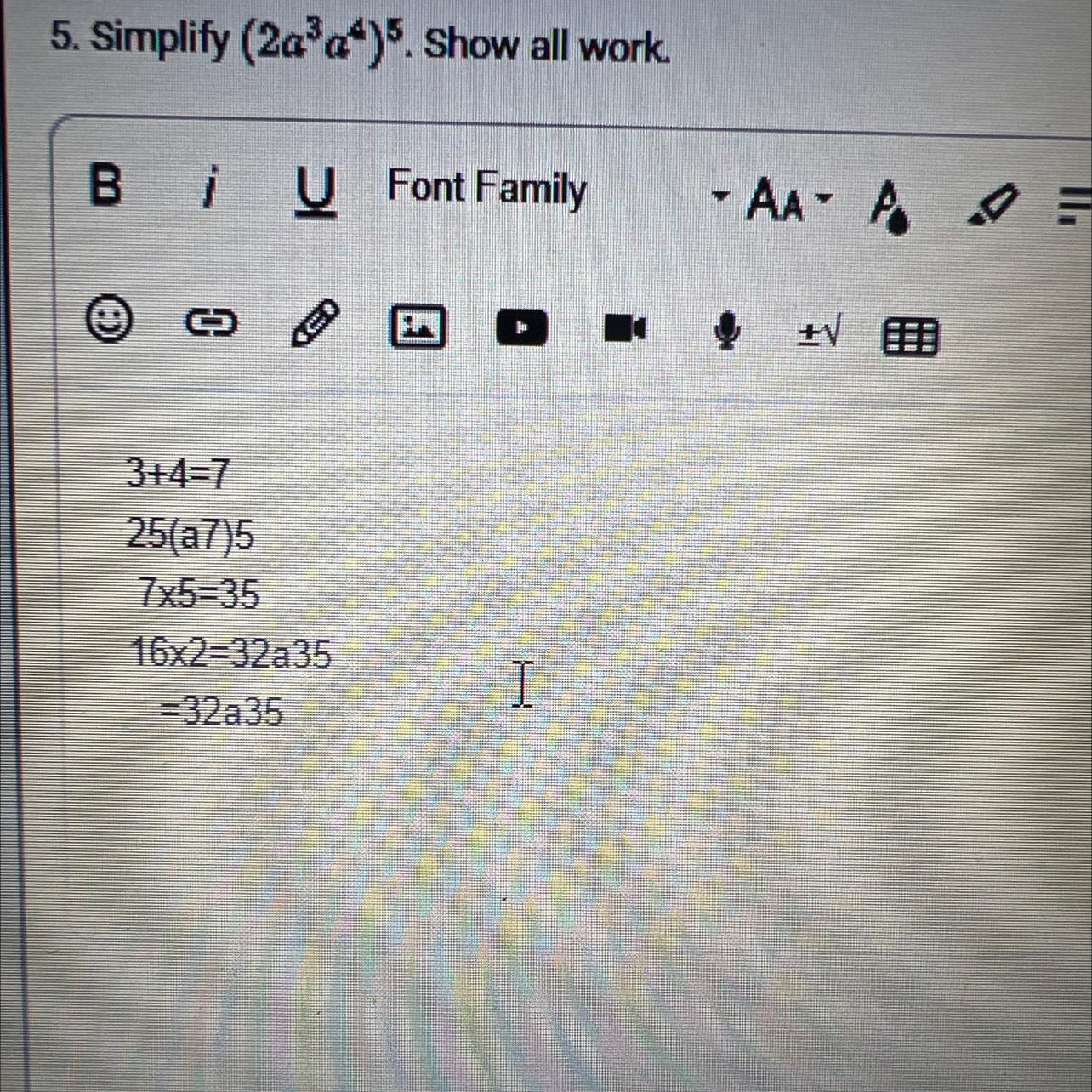

Answers
Answer:
32\(a^{35}\)
Step-by-step explanation:
using the rules of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
\((a^m)^{n}\) = \(a^{mn}\)
\((2a^3a^4)^{5}\)
= (2\(a^{(3+4)}\) )^5
= \((2a^7)^{5}\)
raise each term inside the parenthesis to power 5
= \(2^{5}\) × \(a^{7(5)}\)
= 32\(a^{35}\)
Answer:
32\(a^{35}\)
Step-by-step explanation:
using the rules of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
\((a^m)^{n}\) = \(a^{mn}\)
\((2a^3a^4)^{5}\)
= (2\(a^{(3+4)}\) )^5
= \((2a^7)^{5}\)
raise each term inside the parenthesis to power 5
= \(2^{5}\) × \(a^{7(5)}\)
= 32\(a^{35}\)
14.62 + (-11.302)
what is the answer?
Answers
Answer:
Simplifying
14.62 + (-11.302) = 0
14.62 + (-11.302) = 0
Combine like terms: 14.62 + (-11.302) = 3.318
3.318 = 0
Solving
3.318 = 0
Couldn't find a variable to solve for.
This equation is invalid, the left and right sides are not equal, therefore there is no solution.
Hope this helps!
Have a great day!
(1,000,000) + (3,00,000) + (60,000)+(2,000) + (700)+( 40)+8
Answers
Step-by-step explanation:
________________________________________________________________
\((1,000,000) + (3,00,000) + (60,000)+(2,000) + (700)+( 40)+8 \\ = 1300000 + 62000 + 740 + 8 \\= 1362000 + 748 \\= 1362748\)
________________________________________________________________
hope it helped you:)
Use the histogram to answer the following questions.
Frequency
The frequency of the class 90-93 is
The frequency of the class 94-97 is
This means that a total of
5.5
5
4.5
Your answers should be exact numerical values.
The frequency of the class 86-89 is
86
94
90
Duration of Dormancy (minutes)
dormancy periods were recorded.
Answers
The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes, hence it is the same as a relative frequency.
The total number of periods is given as follows:
5 + 6 + 4 = 15.
The frequency of each class is given as follows:
86 - 89: 5/15 = 1/3.90 - 93: 6/15 = 2/5.94 - 97: 4/15.Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

Solve |x| + 7 < 4
Please help, thank yoooouuuuuuuuu

Answers
Answer:
0 theres no solution
Step-by-step explanation:
Roy is skiing on a circular ski trail that has a radius of 0.7 km. Roy starts at the 3-o'clock position and travels 2.15 km in the counter-clockwise direction. a. How many radians does Roy sweep out? _____ radians Preview b. When Roy stops skiing, how many km is Roy to the right of the center of the ski trail? _____ v km Preview c. When Roy stops skiing, how many km is Roy above of the center of the ski trail? _____ * km
Answers
Part a: Roy sweeps out 2.15/0.7 radians.
Part b: When Roy stops skiing, he is cos(3.071)(0.7) km to the center of the ski trial
Part c: When Roy stops skiing he is sin(3.071)(0.7) km above the centre of the ski trail
The radius of the ski trail= 0.7 km
Roy starts 3 o'clock position and travels 2.15 km in the counter-clockwise direction.
Let O be the centre of ski trial, A be the starting point(3-o'clock position) and consider he is now at point B.
Now, using the formula for arc length.
Arc length=(Radius)(angle at center)
2.15=(0.7)θ
θ=2.15/0.7
Roy sweep out 2.15/0.7 radians.
Part b:
When Roy stops skiing how many km is Roy to the right of the ski trial
In part, a figure draws the vertical line from point B on the horizontal line. Get the right-angle triangle
Here to find the length OP. In right angle triangle cos θ=Adjacent side/hypotenuse,
As in part, a central angle is 2.15/0.7=3.071.
Therefore,
cos(3.071)=OP/0.7
OP=cos(3.071)(0.7)
cos(3.071)(0.7) km.
Part c:
When Roy stops skiing how many km is Roy above the centre of the ski trial
From figure part of part b, we have to calculate side BP.
In right angle triangle sin(θ)=Opposite side/hypotenuse
Therefore,
sin(3.071)=BP/0.7
BP=sin(3.071)/(0.7)
sin(3.071)(0.7) km.
Learn more about circle:
https://brainly.com/question/11833983
#SPJ4


Is this one correct? Let me know please

Answers
Answer:
linear dimensions: 2 : 7areas: 4 : 49volumes: 8 : 343Step-by-step explanation:
You want the area and volume ratios when two figures have a similarity ratio of 2 : 7.
AreaThe ratio of areas is the square of the similarity ratio:
2² : 7² = 4 : 49
VolumeThe ratio of volumes is the cube of the similarity ratio:
2³ : 7³ = 8 : 343
__
Additional comment
It can help to think about the units of area and volume. For linear dimensions in inches, area dimensions are in square inches, and volume dimensions are cubic inches. Any ratio of inches will be squared when those inch dimensions are used for area, and will be cubed when volume is computed.
side length of a square or cube: smaller: 2", larger: 7"
area of the square: smaller: 2² in², larger: 7² in² or 4 in² and 49 in²
volume of the cube: smaller: 2³ in³, larger: 7³ in³ or 8 in³ and 343 in³
<95141404393>
Brainliest plz plz plz

Answers
Answer:
10/12
Step-by-step explanation:
use multiplication to explain why 1/2 divided by 3 equals 1/6
Answers
Answer:
Imagine you have half of a cookie. You break it into three pieces to share with friends. You keep one piece, so you have 1/6 of the entire cookie. You can use multiplication to check your work. 1/6x3 =3/6 of 1/2 :D
Step-by-step explanation:
Given that 5 miles is 8 km, convert 17.8 miles to km.
Answers
Answer:
\(28km\)
Step-by-step explanation:
\(5miles = 8km\)
\(17.8miles = x\)
\( \frac{17.8}{5} \times 8km\)
\(x = 28km\)
Supervisor: "I think you have been doing a great job, but you haven't been signing many people up for our new service feature. I want you to set a goal of signing up 25% of your new customers for our new service feature."
Representative: "If I get 96 new customers that means I have to get __________ of them to sign up for the new service feature."
Answers
It have get \(24\) customer of them to sign up for the new service feature.
Given:
Sign up percentage is \(25\) %.
\(96\) customer.
To find the solution by,
Multiply customer and sign up
\(=96*25\)%
\(=96*\frac{25}{100} \\\\=2400/100\\\\=24\)
Thus, it have get \(24\) customer of them to sign up for the new service feature.
For information,
https://brainly.com/question/18286302
What is the FORMULA for the VOLUME of a CONE?
Answers
Answer:
V = 1/3 * π * r^2 * h OR V = π * r^2 * h/3
Step-by-step explanation:
hope it will help you dear
you told only formula if you need derevation then say :)

Will give brainliest answer

Answers
Answer:
EquivalentNot equivalentEquivalentStep-by-step explanation:
For \(3^5^m\):
Just like \(9^{0.5m}\) · \(9^{2m}\), \(3^5^m\) equates to \(243^m\).
For \(81^m\):
\(81^m\) does not equate to \(9^{0.5m}\) · \(9^{2m}\).
For \(9^{2.5m}\):
After applying the exponent rule to the equation, it came out to \(9^{2.5m}\).
5
Select the correct answer.
How does the diagram illustrate why the sum of the lengths of two sides of a triangle cannot be less than the length of the third side of the triangle?
의
4.6
12
3
O A. by showing the two sides with lengths 4 and 3 will only meet when the angle between them is large
O B.
by showing the two sides with lengths 4 and 3 can always meet to form a vertex
OC. by showing the two sides with lengths 4 and 3 will only meet when they lie on the third side
OD. by showing the two sides with lengths 4 and 3 can never meet to form a vertex
Reset
Next
Answers
Why the length of the third (3) side of a triangle cannot be less than the total of any two (2) of its sides is shown in the diagram: B. by demonstrating that two sides with lengths of 4 and 3 cannot ever come together to form a vertex.
What is a triangle?The definition of a triangle is a two-dimensional geometric figure with exactly three (3) sides, three (3) vertices, and three (3) angles. According to the length of their sides, triangles fall into one of the following three (3) categories:
Equal-sided triangletriangular isoscelesTriangular scaleAccording to the Triangle Inequality Theorem, any two (2) triangles' side lengths added together must be bigger than the length of the triangle's third (2) side. In light of the Triangle Inequality Theorem, this finally means that the total of the lengths of any two (2) sides of a triangle cannot be less than the length of the third (3) side of the triangle.By applying the Triangle Inequality Theorem to this diagram (see attachment), we have:
4 + 12 > 3 (True).
3 + 12 > 4 (True).
4 + 3 > 12 (False).
To learn more about triangle refer to:
https://brainly.com/question/1058720
#SPJ1
1. The proportion, p, of consumers who shop with coupons
is the ratio of the number, C, of consumers who use coupons
to the number, N, of consumers asked. Write an equation
for the proportion of consumers who shop with coupons.
Answers
The equation for the proportion, p, of consumers who shop with coupons is: p = C/N where C is the number of consumers who use coupons and N is the total number of consumers asked.
What is equation?An equation is a mathematical statement that indicates the equality of two expressions. It consists of two expressions separated by an equal sign (=). The expression on the left side of the equal sign is equivalent to the expression on the right side. Equations can have one or more variables, which are usually represented by letters such as x, y, or z. The goal in solving an equation is to determine the value(s) of the variable(s) that make the equation true. This involves manipulating the expressions on both sides of the equal sign using algebraic operations such as addition, subtraction, multiplication, and division, to isolate the variable on one side of the equation. Equations are used in many areas of mathematics and science to represent relationships between variables and to solve problems. They are also used in various fields such as engineering, physics, and economics to model real-world situations and make predictions based on mathematical analysis.
Here,
This equation represents the ratio of the number of consumers who use coupons to the total number of consumers. It is commonly used in statistics and market research to measure the prevalence of a certain behavior or preference among a population. By calculating the proportion of consumers who use coupons, businesses can make informed decisions about their pricing strategies, promotions, and advertising campaigns.
To know more about equation,
https://brainly.com/question/2228446
#SPJ9
One of the assumptions underlying the theory of control charting is that successive plotted points are independent of one another. Each plotted point can signal either that a manufacturing process is operating correctly or that there is some sort of malfunction. Even when a process is running correctly, there is a small probability that a particular point will signal a problem with the process. Suppose that this probability is 0.05. What is the probability that at least one of 10 successive points indicates a problem when in fact the process is operating correctly? What is the probability that at least one of 40 successive points indicates a problem when in fact the process is operating correctly?
Answers
Answer:
a) the probability that at least one of 10 successive points indicates a problem when in fact the process is operating correctly is 0.4013
b) the probability that at least one of 40 successive points indicates a problem when in fact the process is operating correctly is 0.8715
Step-by-step explanation:
following how the independence multiplication rule works,
i.e finding p(A)' which is 1 - p(No problem) because what we need is an intersection not a union so;
a) 10 successive points
probability (problem) = 0.05
probability (No problem) = 0.95
required probability = 1 - [probability (No problem)]^10
= 1 - (0.95)^10
= 1 - 0.5987
= 0.4013
the probability that at least one of 10 successive points indicates a problem when in fact the process is operating correctly is 0.4013
b) 40 successive points
probability (problem) = 0.05
probability (No problem) = 0.95
required probability = 1 - [probability (No problem)]^40
= 1 - (0.95)^40
= 1 - 0.1285
= 0.8715
the probability that at least one of 40 successive points indicates a problem when in fact the process is operating correctly is 0.8715
Find three nonzero vectors a, b, and c such that a × b = a × c != 0 but b != c.
Answers
9514 1404 393
Answer:
a = {1, 2, 3}, b = (2, 4, 7}, c = (-3/14, -3/7, 5/14}
Step-by-step explanation:
For the above vectors, ...
a × b = a × c = (2, -1, 0)
__
Here, c is found to be a scaled version of (a×(a×b)).
My Account Need Help? Table of Contents
Module 5: Alcohol and Other Drugs
Time Elapred: OC-S57:45
The Remaining:00-00:00
Please answer the following question about the video you just watched.
Video Question: What noise sounds at the end of a
segment?
a) A horn blows
b) A bell rings
c) A song plays
d) There is no sound
Copyright 2014, American Safety Council, Inc. - All Rights Reserved
A
Logout
C
Answers
The horns are frequently used as a signal to indicate the end of a segment or a specific task. Hence, a horn blows is the noise that sounds at the end of a segment.
The noise that sounds at the end of a segment is A horn blows.
In geometry, a segment is a part of a line that connects two points.
For example, line segment AB, which is denoted by AB, connects point A and point B and can be visualized as a portion of a line.
In general, line segments are denoted by their endpoints.
A horn is a cone-shaped instrument that is often used as a warning signal or a musical instrument.
However, it is important to note that noise can occur at the end of a segment in certain contexts and situations.
For example, in the context of audio or video editing, you can apply fade-out effects or specific sound effects to signal the end of a segment.
However, these sounds are not universally applicable and depend on the specific creative choices and technical aspects of the project.
In the transportation sector, horns are commonly used to alert pedestrians and other drivers of an oncoming vehicle's presence.
The sound of a horn is usually a sharp and loud noise that is difficult to ignore.
As a result, horns are frequently used as a signal to indicate the end of a segment or a specific task. Hence, a horn blows is the noise that sounds at the end of a segment.
For more questions on specific task:
https://brainly.com/question/29221862
#SPJ8