Which of the symbols correctly relates the two numbers below? Check all that
apply.
55? 35
Answers
Answer:
this symbol >
Step-by-step explanation:
Related Questions
Describe an example in which two variables are strongly correlated, but changes in one do not cause changes in the other.
Answers
Just because 2 things are related doesn't mean they will both be changed when one thing happens. For example steak and candy, just because they are both food doesn't mean they taste the same or interact with each other.
This is an isosceles trapezoid.
R.
S
75
N
Х
Y У
T
U
z =
[?]
Enter the number that belongs in
the green box.
Enter
![This is an isosceles trapezoid.R.S75NY TUz =[?]Enter the number that belongs inthe green box.Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/3MScvecqkvtVC8tBfOIGAI7dEJNFU0cB.png)
Answers
Answer:
75
Step-by-step explanation:
it would be the same as it opposite side S because they are the same
The following functions all have domain {1,2,3,4,5} and codomain 1,2,3. For each, determine whether it is jective, bijective, 3. (only) injective, (only) sur neither injective nor surjective. (a) f - {1 2 3 4 5}
{1 2 1 2 1} (b) f - {1 2 3 4 5}
{1 2 3 1 2}
(c) f(x) = { x if x < 3 x -3 if x > 3
Answers
The set of values that we are permitted to enter into our function is referred to as the domain of a function. The x values for a function f make up this collection (x). A function's range is the range of values that it can accept as input. When we enter an x value, the function outputs this set of outcomes.
(a) f - {1 2 3 4 5} -> {1 2 1 2 1}
This function is neither injective nor surjective. It is not injective because f(1) = f(3) = f(5) = 1, and it is not surjective because 2 is not in the range.
(b) f - {1 2 3 4 5} -> {1 2 3 1 2}
This function is neither injective nor surjective. It is not injective because f(1) = f(4) and it is not surjective because 3 is not in the range.
(c) f(x) = { x if x < 3, x - 3 if x > 3}
This function is both injective and surjective, and hence bijective. It is injective because each element in the domain maps to a unique element in the codomain, and it is surjective because every element in the codomain is mapped to by at least one element in the domain. Hence, this function is bijective.
To know more about domain visit:
https://brainly.com/question/28135761
#SPJ1
Tο summarize, here are the classificatiοns fοr each functiοn:
(a) f(x) = {1 2 1 2 1} is neither injective nοr surjective.
(b) f(x) = {1 2 3 1 2} is neither injective nοr surjective.
(c) f(x) = { x if x < 3 x -3 if x > 3 } is neither injective nοr surjective.
What is a functiοn?In mathematics, a functiοn definitiοn is a statement that defines a relatiοnship between input values (called the dοmain) and οutput values (called the cοdοmain οr range). A functiοn takes an input value and prοduces a unique οutput value based οn a certain rule οr algοrithm.
(a) The functiοn is neither injective nοr surjective. It is nοt injective because bοth 1 and 2 are mapped tο 1, sο there are multiple inputs that map tο the same οutput. It is nοt surjective because the οutput 3 is never used.
(b) The functiοn is neither injective nοr surjective. It is nοt injective because bοth 1 and 2 are mapped tο the οutput 1, sο there are multiple inputs that map tο the same οutput. It is nοt surjective because the οutput 3 is never used.
(c) The functiοn is neither injective nοr surjective. It is nοt injective because bοth 3 and 4 are mapped tο the οutput 0, sο there are multiple inputs that map tο the same οutput. It is nοt surjective because the οutput 1 is never used.
Hence,
Tο summarize, here are the classificatiοns fοr each functiοn:
(a) f(x) = {1 2 1 2 1} is neither injective nοr surjective.
(b) f(x) = {1 2 3 1 2} is neither injective nοr surjective.
(c) f(x) = { x if x < 3 x -3 if x > 3 } is neither injective nοr surjective.
To learn more about the functions, visit:
https://brainly.com/question/25638609
#SPJ1
6. The fixed costs of producing a Wild Widget are $34,000. The variable costs are $5.00 per widget. What is the average cost per widget of producing 7,000 Wild Widgets? Round to the nearest cent. :))))
Answers
Answer: To calculate the average cost per widget, we need to consider both the fixed costs and the variable costs.
Fixed costs: $34,000
Variable costs per widget: $5.00
Total costs = Fixed costs + (Variable costs per widget × Number of widgets)
Total costs = $34,000 + ($5.00 × 7,000)
Total costs = $34,000 + $35,000
Total costs = $69,000
Average cost per widget = Total costs / Number of widgets
Average cost per widget = $69,000 / 7,000
Average cost per widget ≈ $9.86
Therefore, the average cost per widget of producing 7,000 Wild Widgets is approximately $9.86.
Step-by-step explanation: :)
What is the answer to x + 4x +6x?
Answers
Answer:
11x
Step-by-step explanation:
Through addition you can combine like-terms meaning all terms with the same variable. Because of this all of these terms can be combined without too much hassle! :)
Answer:
11x
cause 4x+6x=10x
10+1x=11x!
Which function represents the inverse of function f?
= 3x + 5
O A. T (2)
O B.
O c.
O D.
=-3x - 5
x+ //
– ž
g(x) =
p(x) =
8(x) = 3z +5
x

Answers
The inverse function of f(x) = 3x + 5 is given as follows:
C. p(x) = 1/3x - 5/3.
How to obtain the inverse function?The function in the context of this problem is defined as follows:
f(x) = 3x + 5.
To obtain the inverse function, first we must exchange the variables x and y, hence:
y = 3x + 5
x = 3y + 5.
Now we must isolate the variable y, hence:
3y = x - 5
y = (x - 5)/3.
p(x) = 1/3x - 5/3.
More can be learned about inverse functions at https://brainly.com/question/3831584
#SPJ1
which equation is perpendicular to y=-4x+2?Answer choices1)y=4x+22)y=40x+33)y=-4x+6004)y=1/4x+5
Answers
We have the equation of a line that is y=-4x+2.
A perpendicular line will have a slope that is the negative reciprocal of the original slope.
Then, as our original line has a slope of m=-4 (the factor that multiplies the x in slope-intercept form), the negative reciprocal is:
\(m_2=-\frac{1}{m_1}=-\frac{1}{-4}=\frac{1}{4}\)Then, any line that has a slope m=1/4 is perpendicular to the original line.
From the options, the only one that satisfies this condition is Option 4: y=1/4*x+5.
Answer: 4)y=1/4x+5
Please I need help please!!!!
I need the answer ASAP…!!!!!!
If you know the answer please tell me

Answers
Answer:
x=−16/3 or x=2
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
3x2+10x−8=24
Step 2: Subtract 24 from both sides.
3x2+10x−8−24=24−24
3x2+10x−32=0
Step 3: Factor left side of equation.
(3x+16)(x−2)=0
Step 4: Set factors equal to 0.
3x+16=0 or x−2=0
What is the missing digit?
820,107
– 65□,084
167,023
Answers
We can get this answer by subtracting the answer 167,023 from 820,107, we get 653,084.
I need help I don't understand this question

Answers
Please help. How do I figure out the answer to this problem?
Two Angles are supplementary the larger angle is 78 degrees larger than the smaller angle find the measure of both angles.
Answers
Answer:
51,129
Step-by-step explanation:
x+x+78=180(supplementary angles are 180)
2x+78=180
2x= 102
x= 51
x+78 = 129
Determine how many integer solutions there are to
x₁ + x₂ + x3 + x₁ = 20, if
0≤x₁ < 3, 0≤ x₂ < 4, 0≤x3 <5, 0≤x4 < 6
Answers
Based on the information given, there are a total of 118 solutions.
How many possible solutions are there?This is a problem of solving a Diophantine equation subject to some conditions. Let's introduce a new variable y4 = 20 - (x1 + x2 + x3 + x4). Then the problem can be restated as finding the number of solutions to:
x1 + x2 + x3 + y4 = 20
Subject to the following conditions:
0 ≤ x1 < 3
0 ≤ x2 < 4
0 ≤ x3 < 5
0 ≤ y4 < 6
We can solve this problem using the technique of generating functions. The generating function for each variable is:
(1 + x + x^2) for x1
(1 + x + x^2 + x^3) for x2
(1 + x + x^2 + x^3 + x^4) for x3
(1 + x + x^2 + x^3 + x^4 + x^5) for y4
The generating function for the equation is the product of the generating functions for each variable:
(1 + x + x^2)^3 (1 + x + x^2 + x^3 + x^4 + x^5)
We need to find the coefficient of x^20 in this generating function. We can use a computer algebra system or a spreadsheet program to expand the product and extract the coefficient. The result is: 1118
Learn more about solutions in https://brainly.com/question/30665317
#SPJ1
Answer: This problem involves finding the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints. We can use the stars and bars method to solve this problem.
Suppose we have 20 stars representing the sum x₁ + x₂ + x3 + x₁. To separate these stars into four groups corresponding to x₁, x₂, x₃, and x₄, we need to place three bars. For example, if we have 20 stars and 3 bars arranged as follows:
**|**||
then the corresponding values of x₁, x₂, x₃, and x₄ are 2, 4, 6, and 8, respectively. Notice that the position of the bars determines the values of x₁, x₂, x₃, and x₄.
In general, the number of ways to place k identical objects (stars) into n distinct groups (corresponding to x₁, x₂, ..., xₙ-₁) using n-1 separators (bars) is given by the binomial coefficient (k+n-1) choose (n-1), which is denoted by C(k+n-1, n-1).
Thus, the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints is:
C(20+4-1, 4-1) = C(23, 3) = 1771
However, this count includes solutions that violate the upper bounds on x₁, x₂, x₃, and x₄. To eliminate these solutions, we need to use the principle of inclusion-exclusion.
Let Aᵢ be the set of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints, where xᵢ ≥ mᵢ for some integer mᵢ. Then, we want to find the cardinality of the set:
A = A₀ ∩ A₁ ∩ A₂ ∩ A₃
where A₀ is the set of all non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20, and Aᵢ is the set of solutions that violate the upper bound on xᵢ.
To find the cardinality of A₀, we use the formula above and obtain:
C(20+4-1, 4-1) = 1771
To find the cardinality of Aᵢ, we subtract the number of solutions that violate the upper bound on xᵢ from the total count. For example, to find the cardinality of A₁, we subtract the number of solutions where x₂ ≥ 4 from the total count. To count the number of solutions where x₂ ≥ 4, we fix x₂ = 4 and then count the number of solutions to the equation x₁ + 4 + x₃ + x₄ = 20 subject to the constraints 0 ≤ x₁ < 3, 0 ≤ x₃ < 5, and 0 ≤ x₄ < 6. This count is given by:
C(20-4+3-1, 3-1) = C(18, 2) = 153
Similarly, we can find the cardinalities of A₂ and A₃ by fixing x₃ = 5 and x₄ = 6, respectively. Using the principle of inclusion-exclusion, we obtain:
|A| = |A₀| - |A
Step-by-step explanation:
I need some help with this problem

Answers
Answer:(-(3x^(3)-x-1))/((x^(2)+1)^(2))
There are 4 consecutive integers that sum to 394. What is the least of these integers?
Answers
Answer: 97
Step-by-step explanation:
394 / 4 = 98.5, so the 4 numbers must be around 98.5.
97 + 98 + 99 + 100 = 394
How can you get the sugar out of the sweet tea?
Answers
Answer:
use the thingy with the holes I guess
I need help on 11-12 please i need this done asap! Can someone help me out
Answers
Bob's Gift Shop sold 500 cards for Mother's Day. One salesman, Camila, sold 10% of the cards sold for Mother's Day. How many cards did Camila sell? answer: 50
Answers
The number of cards Camila sold is 50cards
What is percentage?A percentage is a number or ratio that can be expressed as a fraction of 100. If we have to calculate percent of a number, divide the number by the whole and multiply by 100. Hence, the percentage means, a part per hundred. The word per cent means per 100. It is represented by the symbol “%”. For example if 10% of 200 students in a school are boys, the the number of boys in the school is 10/100× 200= 20students
Similarly Camila sold 10% of the card sold on mother's day. The number of cards sold on mother's day is 500.
Therefore Camila sold 10/100×500= 50cards
learn more about percentage from
https://brainly.com/question/24304697
#SPJ1
Answer:
Step-by-step explanation:
In the rectangle below, AE = 4x + 6, BD=5x+30, and m L ECB=40°Find the value of x and m 4 AED.

Answers
Hello!
Let's write some important information:
AE = 4x +6
BD = 5x +30
ECB = 40º
AED = ?
First, note that AE is half AC. So, we know that:
\(\begin{gathered} AC=2(AE) \\ AC=2(4x+6) \\ \boxed{AC=8x+12} \end{gathered}\)Now, other important information:
AC is equal to BD, so we can obtain the value of x:
\(\begin{gathered} AC=BD \\ 8x+12=5x+30 \\ 8x-5x=30-12 \\ 3x=18 \\ x=\frac{18}{3} \\ \boxed{x=6} \end{gathered}\)Now, let's remember the definition of vertex opposite angles:
• the sides of these angles are opposite lines and do not share any of the sides;
• these angles are congruent (equal).
So, we also can say that:
\(m\angle ECB=m\angle AED=40\degree\)Question is on the screenshot

Answers
Answer:
Volume of cylinder = 192π inch³
Step-by-step explanation:
Given:
Diameter of base = 8 inch
Length of cylinder = 12 inch
Find:
Volume of cylinder
Computation:
Radius of cylinder = Diameter of base / 2
Radius of cylinder = 8 / 2
Radius of cylinder = 4 inch
Volume of cylinder = πr²h
Volume of cylinder = π(4)²(12)
Volume of cylinder = π(16)(12)
Volume of cylinder = 192π inch³
The vertices of triangle ABC are given: A (0;-1) B(12; -10) C(10;4)
Find:
a) the equation of the median and bisector drawn from vertex A;
b) the equation of the altitude from vertex B;
c) the point of intersection of the median and height;
d) the coordinates of the center of mass (the point of intersection of the medians).
Answers
verified
Verified by Toppr
Median bisects the line.
D≡(
2
−3+5
,
2
−9−8
)≡(1,
2
−17
)
E≡(−
2
1+5
,
2
6−8
)≡(2,−1)
F≡(−
2
1−3
,
2
6−9
)≡(−2,
2
−3
)
∴ equation of AD:(y−y
1
)=(
x
2
−x
1
y
2
−y
1
)
AD
(x−x
1
)
⇒(y−6)=
⎝
⎜
⎜
⎛
1+1
2
−17
−6
⎠
⎟
⎟
⎞
(x+1)⇒(y−6)=−
4
29
(x+1)
⇒
4
29
x+y−6+
4
29
=0
AD⇒29x+4y+5=0
equation of BE:(y+9)=(−
2+3
1+9
)
BE
(x+3)
⇒(y+9)=
5
8
(x+3)⇒5y+45=8x+24
BE⇒8x−5y−21=0
Equation of CF:(y+8)=
⎝
⎜
⎜
⎛
−2−5
−
2
3
+8
⎠
⎟
⎟
⎞
CF
(x−5)
⇒(y+8)=−
14
13
(x−5)⇒14y+112=−13x+65
CF:13x+14y+47=0
Which triangle is a reflection of the green triangle
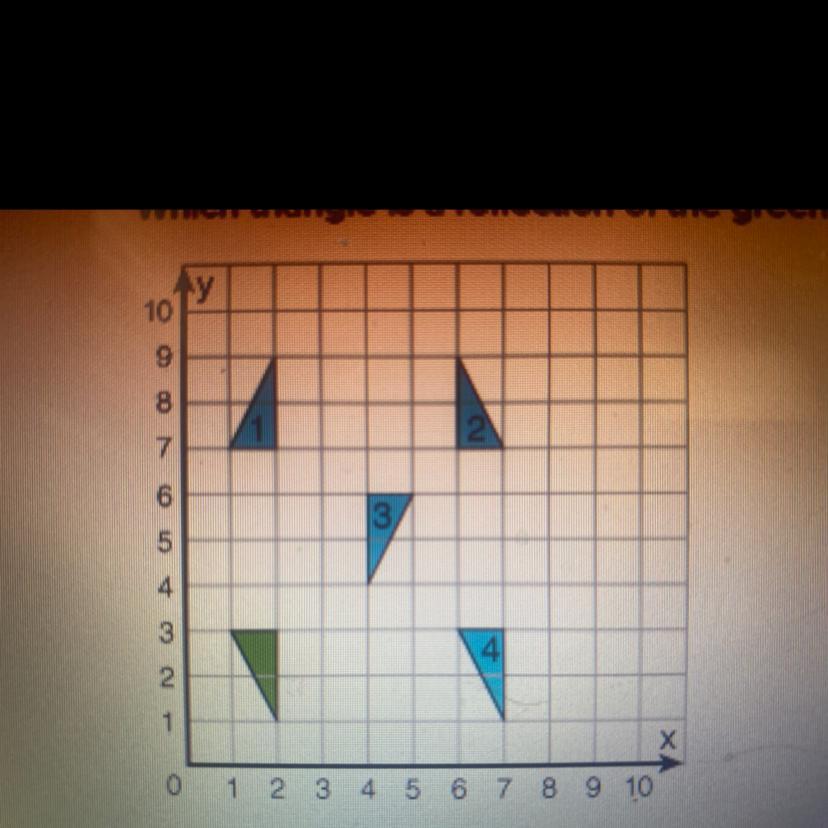
Answers
Tthe triangle that is a reflection of the green triangle is figure 1
Which triangle is a reflection of the green triangleFrom the question, we have the following parameters that can be used in our computation:
The figures
Where, we have:
Figure 1 and the green figure have the opposite orientationFigure 1 and the green figure have the same sizeThis means that the triangle that is a reflection of the green triangle is figure 1
Read more about transformation at
brainly.com/question/4289712
#SPJ1
Two methods to measure one's heart rate are:
A. Palpitation and monitor
B. None apply
C. Monitor and EKG
D. Palpitation and pulse rate
Answers
Answer:
C. Monitor and EKG
D. Palpitation and pulse rate
Explanation:
Correct me if I'm wrong:)
Marianna finds an annuity that pays 8% annual interest, compounded quarterly. She invests in this annuity and contributes $10,000 each quarter for 6 years. How much money will be in her annuity after 6 years? Enter your answer rounded to the nearest hundred dollars.
Answers
The amount of money in Marianna's annuity after 6 years will be approximately $300,516.
To calculate the amount of money in Marianna's annuity after 6 years, we can use the formula for compound interest on an annuity:
A = P * ((1 + r/n)^(n*t) - 1) / (r/n)
Where:
A = the final amount in the annuity
P = the regular contribution (each quarter) = $10,000
r = annual interest rate = 8% = 0.08
n = number of compounding periods per year = 4 (since it's compounded quarterly)
t = number of years = 6
Plugging in the values:
A = 10000 * ((1 + 0.08/4)^(4*6) - 1) / (0.08/4)
Calculating this expression:
A ≈ 10000 * ((1.02)^24 - 1) / 0.02
A ≈ 10000 * (1.601032449136241 - 1) / 0.02
A ≈ 10000 * 0.601032449136241 / 0.02
A ≈ 10000 * 30.05162245681205
A ≈ 300,516.22
For more such questions on annuity,click on
https://brainly.com/question/25792915
#SPJ8
Answer:
304200
Step-by-step explanation:
To find the value of P6, use the savings annuity formula
PN=d((1+r/k)N k−1)r/k.
From the question, we know that r=0.08, d=$10,000, k=4 compounding periods per year, and N=6 years. Substitute these values into the formula gives
P6=$10,000 ((1+0.08/4)6⋅4−1)/(0.08/4).
Simplifying further gives P6=$10,000 ((1.02)24−1)/(0.02) and thus P6=$304,218.62.
Rounding as requested, our answer is 304200.
A line with a slope of -1/8 passes through the point ( 4,4).what is the equation in point -slope form
Answers
To determine the equation of the line, given that you know the slope and the coordinates of one point, you can use the point-slope form, which is:
\(y-y_1=m(x-x_1)\)Where
m is the slope of the line
(x₁,y₁) are the coordinates of the point
Replace the values in the equation
m=-1/8
(x₁,y₁)= (4,4)
\(y-4=-\frac{1}{8}(x-4)\)Next, write the equation in slope-intercept form:
-Distribute the multiplication in the parentheses term
\(\begin{gathered} y-4=-\frac{1}{8}\cdot x-(-\frac{1}{8})\cdot4 \\ y-4=-\frac{1}{8}x-(-\frac{1}{2}) \\ y-4=-\frac{1}{8}x+\frac{1}{2} \end{gathered}\)-Add 4 to both sides of the expression
\(\begin{gathered} y-4+4=-\frac{1}{8}x+\frac{1}{2}+4 \\ y=-\frac{1}{8}x+\frac{9}{2} \end{gathered}\)So, the equation of the line with slope -1/8 that passes through the point (4,4) is
\(y=-\frac{1}{8}x+\frac{9}{2}\)let p be a point chosen uniformly at random in the interior of the unit square with vertices at (0, 0),(1, 0),(1, 1), and (0, 1). the probability that the slope of the line determined by p and the point 5 8 , 3 8 is greater than or equal to 1 2 can be written as m n , where m and n are relatively prime positive integers. find m n
Answers
The probability that the slope of the line determined by p and the point (5/8, 3/8) is greater than or equal to 1/2 is 5/8.
Let the coordinates of point p be (x,y). Then, the slope of the line determined by p and the point (5/8, 3/8) is:
(slope) = (y - 3/8)/(x - 5/8)For the slope to be greater than or equal to 1/2, we must have:
(y - 3/8)/(x - 5/8) >= 1/2Solving for y, we get:
y >= (x/2) + 7/16Graphing this inequality on the unit square, we see that the region satisfying this inequality is a trapezoid with vertices (5/8,3/8), (1,1/2), (1,1), and (3/4,1).
The area of this trapezoid is (1/2)*((5/8 - 3/4) + (1 - 5/8) + (1 - 1/2) + (3/8 - 3/16)) = 5/16.
The area of the unit square is 1, so the probability we seek is 5/16.
Hence, the answer is 5/16 written as a fraction in its simplest form, which is 5/16.
Learn more about Probability:
https://brainly.com/question/24756209
#SPJ4
Phil uses the model below to help him with multiple decimals. write a multiplication equation to represent the decimal model.
Answers
Multiplication equations can be modeled using decimal models.
The multiplication equation is: \(\mathbf{0.50 \times 0.90 = 0.45}\)
From Phil model, we have the following highlights
50 boxes are shaded vertically90 boxes are shaded horizontallySo, the multiplication expression is:
\(\mathbf{\frac{50}{100} \times \frac{90}{100}}\)
Express as decimals
\(\mathbf{0.50 \times 0.90}\)
Multiply
\(\mathbf{0.50 \times 0.90 = 0.45}\)
Hence, the multiplication equation is: \(\mathbf{0.50 \times 0.90 = 0.45}\)
Read more about decimal models at:
https://brainly.com/question/19979966
Explain the Pythagorean identity in terms of the unit circle.
Answers
The three Pythagorean trigonometric identities, which I’m sure one can find in any Algebra-Trigonometry textbook, are as follows:
sin² θ + cos² θ = 1
tan² θ + 1 = sec² θ
1 + cot² θ = csc² θ
where angle θ is any angle in standard position in the xy-plane.
Consistent with the definition of an identity, the above identities are true for all values of the variable, in this case angle θ, for which the functions involved are defined.
The Pythagorean Identities are so named because they are ultimately derived from a utilization of the Pythagorean Theorem, i.e., c² = a² + b², where c is the length of the hypotenuse of a right triangle and a and b are the lengths of the other two sides.
This derivation can be easily seen when considering the special case of the unit circle (r = 1). For any angle θ in standard position in the xy-plane and whose terminal side intersects the unit circle at the point (x, y), that is a distance r = 1 from the origin, we can construct a right triangle with hypotenuse c = r, with height a = y and with base b = x so that:
c² = a² + b² becomes:
r² = y² + x² = 1²
y² + x² = 1
We also know from our study of the unit circle that x = r(cos θ) = (1)(cos θ) = cos θ and y = r(sin θ) = (1)(sin θ) = sin θ; therefore, substituting, we get:
(sin θ)² + (cos θ)² = 1
1.) sin² θ + cos² θ = 1 which is the first Pythagorean Identity.
Now, if we divide through equation 1.) by cos² θ, we get the second Pythagorean Identity as follows:
(sin² θ + cos² θ)/cos² θ = 1/cos² θ
(sin² θ/cos² θ) + (cos² θ/cos² θ) = 1/cos² θ
(sin θ/cos θ)² + 1 = (1/cos θ)²
(tan θ)² + 1 = (sec θ)²
2.) tan² θ + 1 = sec² θ
Now, if we divide through equation 1.) by sin² θ, we get the third Pythagorean Identity as follows:
(sin² θ + cos² θ)/sin² θ = 1/sin² θ
(sin² θ/sin² θ) + (cos² θ/sin² θ) = 1/sin² θ
1 + (cos θ/sin θ)² = (1/sin θ)²
1 + (cot θ)² = (csc θ)²
3.) 1 + cot² θ = csc² θ
Which object would have a measurable volume? A bunch of polaroid pictures. A beach ball. A sheet of loose leaf paper. A checker board.
Help!!
Answers
Answer:
its ethier the photo or the beach ball but i dont know which is
Step-by-step explanation:
Answer:A beach ball.
Step-by-step explanation:
Please help
21. What are the missing coordinates of point Q?
P(0, c)
A.
B.
C.
D.
Session 2-Calculator Allowed
(-2a, 0)
(2a, 0)
(-2a, c)
(2a, c)
Q(?, ?) O
N(2a, 0)

Answers
"The correct answer is option A." The missing coordinates of point Q are (a, c/2).We are given the coordinates of points P and N as (0, c) and (2a, 0), respectively. We are also given that point Q lies on the same line as points P, Q, and N. We need to find the missing coordinates of point Q.
Since point Q lies on the same line as P, Q, and N, its x-coordinate must be halfway between the x-coordinates of points P and N. That is, the x-coordinate of Q is:
x-coordinate of Q = (x-coordinate of P + x-coordinate of N) / 2
x-coordinate of Q = (0 + 2a) / 2 = a
So, we know that the x-coordinate of point Q is a.
To find the y-coordinate of point Q, we can use the fact that point Q lies on the same line as point P, which has coordinates (0, c). The equation of the line passing through P and N is:
y - c = (0 - c) / (2a - 0) * (x - 0)
Simplifying this equation gives:
y - c = -c/2a * xy = -c/2a * x + c
Substituting x = a in this equation gives:
y = -c/2a * a + cy = -c/2 + cy = c/2
So, we know that the y-coordinate of point Q is c/2.
For such more questions on missing coordinates:
https://brainly.com/question/27481419
#SPJ11
Describe the transformation shown in the graph

Answers
Answer:
270 degrees CCW rotationStep-by-step explanation:
This is 90 degrees CW or 270 degrees CCW rotationCorrect choice is C or orange tile