Which of the given values will make the inequality n - 93 > 175 true?
A n = 82
B n = 105
C n = 268
D n = 300
E n = 312
Answers
In the given choices, both (D) n = 300 and (E) n = 312 satisfies the inequality. So for both these options, the inequality is true.
We can solve for n by adding 93 to both sides of the inequality:
n - 93 > 175
Adding 93 on both sides
n - 93 + 93 > 175 + 93
n > 268
Therefore, the value of n that makes the inequality true is greater than 268.In the given options, n = 300 and n = 312 satisfy this condition. So this is inequality is true for both cases. The answer choice that fits this is (D) n = 300 and (E) n =312.
To know more on inequality
https://brainly.com/question/28823603
#SPJ4
Related Questions
IP A wave on a string is described by the following equation: What is the amplitude of this wave? y=(17 cm)cos(5.1 cmπx−14 sπt) Express your answer using two significant figures. A= Part B What is its wavelength? Express your answer using two significant figures. y=(17 cm)cos(5.1 cmπx−14 sπt) What is its period? Express your answer using two significant figures. T= Part D What is its speed? Express your answer using two significant figures
Answers
The amplitude of the wave is 17 cm, the wavelength is approximately 0.390 cm, the period is approximately 0.449 s, and the speed is approximately 0.868 cm/s.
In the equation given: y = (17 cm)cos(5.1 cmπx−14 sπt)
Part A: The amplitude of the wave is the coefficient of the cosine function, which is the value in front of it. In this case, the amplitude is 17 cm.
Amplitude (A) = 17 cm
Part B: The wavelength of the wave can be determined by looking at the argument of the cosine function. In this case, the argument is 5.1 cmπx. The wavelength is given by the formula:
λ = 2π / k
where k is the coefficient in front of x. In this case, k = 5.1 cmπ.
Wavelength (λ) = 2π / 5.1 cmπ ≈ 0.390 cm
Wavelength (λ) ≈ 0.390 cm
Part C: The period of the wave (T) is the time it takes for one complete oscillation. It can be calculated using the formula:
T = 2π / ω
where ω is the coefficient in front of t. In this case, ω = 14 sπ.
Period (T) = 2π / 14 sπ ≈ 0.449 s
Period (T) ≈ 0.449 s
Part D: The speed of the wave (v) can be calculated using the formula:
v = λ / T
where λ is the wavelength and T is the period.
Speed (v) = 0.390 cm / 0.449 s ≈ 0.868 cm/s
Speed (v) ≈ 0.868 cm/s
Therefore, the amplitude of the wave is 17 cm, the wavelength is approximately 0.390 cm, the period is approximately 0.449 s, and the speed is approximately 0.868 cm/s.
To learn more about wavelength
https://brainly.com/question/14316836
#SPJ11
if a, b, and c are boolean variables, then the value of !(a & !(b & !c)) is the same as which of these expressions: !a || (!b || c) !a || (b & !c) (!a || b) & !c
Answers
The value of the expression is the same as the second option: !a || (b & !c).
What are boolean variables?Boolean variables are variables that can have only one of two possible values: true or false. They are named after the 19th-century mathematician George Boole, who developed a system of logic based on binary values. In computer programming, boolean variables are commonly used to represent conditions or states that can be either true or false, such as whether a certain condition is met or whether a certain task has been completed.
The expression !(a & !(b & !c)) can be simplified using De Morgan's laws and distributive property to obtain:
!(a & !(b & !c)) = !a || (b & !c)
Therefore, the value of the expression is the same as the second option: !a || (b & !c).
Learn more on boolean variables here https://brainly.com/question/13527907
#SPJ1
joy organised a large wedding guests had to choose there meals from beef chicken or vegetarian
1/3 of the guests chose beef
5/12 of the guests chose chicken
69 Of the guests chose vegetarian
How many guests were in the wedding?
Answers
There were total 276 guests in the wedding that Joy organised.
Given,
fraction of the guest that chose beef = 1/3
fraction of the guest that chose chicken = 5/12
fraction of the guest that chose vegetarian = 1 - 1/3 - 5/12 = 1/4
we are asked to find the total number of guests in the wedding:
guests that chose vegetarian = 1/4
guests that chose vegetarian = 69
1/4 of the guest = 69
4/4 of the guest = 69 x 4 = 276
Hence there are total 276 guests in the wedding.
Learn more about Solving equations here:
brainly.com/question/723406
#SPJ9
Gasoline Many drivers of cars that can run on regular gas actually buy premium in the belief that they will get better gas mileage. To test that belief, we use 10 cars from a company fleet in which all the cars run on regular gas. Each car is filled first with - either regular or premium gasoline, decided by a coin toss, and the mileage for that tankful is recorded. Then the mileage is recorded again for the same cars for a tankful of the other kind of gasoline. We don't let the drivers know about this experiment. Here are the results (miles per gallon): a) Is there evidence that cars get significantly better fuel economy with premium gasoline? b) How big might that difference be? Check a 90% confidence interval. c) Even if the difference is significant, why might the company choose to stick with regular gasoline? d) Suppose you had done a "bad thing." (We're sure you didn't.) Suppose you had mistakenly treated these data as two independent samples instead of matched pairs. What would the significance test have found? Carefully explain why the results are so different.
Answers
a) There is not enough evidence to conclude that cars get significantly better fuel economy with premium gasoline.
In order to test the belief that premium gasoline provides better fuel economy, a study was conducted using 10 cars from a company fleet. Each car was randomly assigned either regular or premium gasoline, and the mileage for each tankful was recorded. The data was analyzed to determine if there is a significant difference in fuel economy between the two types of gasoline.
To evaluate this, a paired t-test can be used since the same cars were tested with both types of gasoline. The null hypothesis would be that there is no difference in fuel economy between regular and premium gasoline, while the alternative hypothesis would be that there is a significant difference.
The results of the study would be analyzed using the appropriate statistical test, such as a paired t-test, to determine the p-value. If the p-value is less than the chosen significance level (e.g., 0.05), then there would be evidence to reject the null hypothesis and conclude that there is a significant difference in fuel economy.
Learn more about Gasoline.
brainly.com/question/14588017
Can someone help me with part b? I've been stuck on it for an hour :(

Answers
Answer:
Check explanation
Step-by-step explanation:
You're given the equation
\(A=-0.6t^2 + 37.2t + 243\)
where t is the number of year after 1980.
I guess you'd have learned the average rate of change equation.
\(r=\frac{y_2-y_1}{x_2-x_1}=\frac{f(x_2)-f(x_1)}{x_2-x_1}\)
You're asked to find average rate of change from
\(t_1=2000-1980=20\)
\(t_2=2015-1980=35\)
So lets plug that in
\(r=\frac{A(t_2)-A(t_1)}{t_2-t_1}\)
\(r=\frac{A(35)-A(20)}{35-20}\)
\(r=\frac{[-0.6(35)^2 + 37.2(35) + 243]-[-0.6(20)^2 + 37.2(20) + 243]}{35-20}\)
\(r=\frac{[-0.6(35)^2 + 37.2(35) + 243]-[-0.6(20)^2 + 37.2(20) + 243]}{15}\)
plug that in your calculator to get the answer. I dont have a calculator with me so I can't find the answer.
Answer:
The average rate of change is 4.2 billion kilowatt hours per year.
In other words, the amount of nuclear energy increased, on average, by 4.2 billion kilowatt hours per year from 2000 to 2015.
Step-by-step explanation:
Recall that to find the average rate of change between two points, we simply need to find the slope between the two points.
Hence, to find the average rate of change from 2000 to 2015, find the slope between the points A(20) and A(35):
\(\displaystyle \begin{aligned} m_\text{avg} & = \frac{A(35)-A(20)}{(35)-(20)} \\ \\ & = \frac{(810)-(747)}{15} \\ \\ & = \frac{63}{15} = 4.2\end{aligned}\)
In conclusion, the amount of nuclear energy increased, on average, by 4.2 billion kilowatt hours per year from 2000 to 2015.
cual es la raiz cuadrada de 45
cual es la raiz cuadrada de 92
cual es la raiz cuadrada de 126
Answers
The square root of 45 ≈ 6.7082
The square root of 92 ≈ 9.5917
The square root of 126 ≈ 11.2249
How to solve
The square root of 45 is approximately 6.7082, which is derived from taking the square root of 45 \((\sqrt(45)).\)
For 92, the square root is approximately 9.5917 \((\sqrt(92))\).
As for 126, its square root is around 11.2249 \((\sqrt(126)).\)
These values are approximations because the square roots of 45, 92, and 126 are irrational numbers, meaning their decimal representation is non-repeating and non-terminating.
When working with these square roots in calculations, it is common to either use their approximate values or to keep them in square root form to maintain the highest level of precision.
Read more about square root here:
https://brainly.com/question/428672
#SPJ1
The Question in English
What is the square root of 45
what is the square root of 92
what is the square root of 126
30 drinkers were asked whether they like coffee or tea.
18 like coffee
15 like tea
11 like both
a) how many like coffee or tea?
b) how many like coffee but not tea
c) how many don't like either neither
ENTER YOUR RESPONSE
Answers
Answer:
a)22
b)7
c)8
Step-by-step explanation: its really complicated so ill try my best.
so the say 11 like both coffee and tea so that means that they also added 11 to
the other two sections. so if we take 11 away from 18 we get 7, and that's how many people like coffee and not tea. to get answer c) we need to also subtract 11 from 15, which gets us 4. so we have 11 plus 4 plus 7. and that gets us 22. so 30 subtract 22 gets us 8 so 8 people don't like tea or coffee. 22 is also the answer to a). did you get that? i hope so
12) The red ribbon is 21 centimeters longer than the blue nbbon. The blue ribbon is 48 centimeters shorter than the green ribbon The green ribbon is(2meters(35 centimeters long. How long is the red ribbon? - 253 48 2 IS red ribbon 21 cm blue ribbon [ 48cm WI green ribbon [ 2m 35cm T25 2 meters 1 니 The red ribbon is centimeters long
Answers
Explanation:
Red ribbon = 21cm + blue ribbon
Blue ribbon = green ribbon - 48 cm
Green ribbon = 2m 35cm
converting the length to centimeter:
100cm = 1m
Green ribbon = 2(100) + 35cm = 200 + 35
Green ribbon = 235cm
Blue ribbon = 235cm - 48cm
Blue ribbon = 187cm
Red ribbon = 21cm + 187cm
can you see the workings?please resp
the first blanks options are -2 , -1/2 , 2 , 1/2
The seconds are -5 , -3 , 5, 3
the thirds are -2, -1, 2, 1
and the fourths are -2, -1, 2, 1
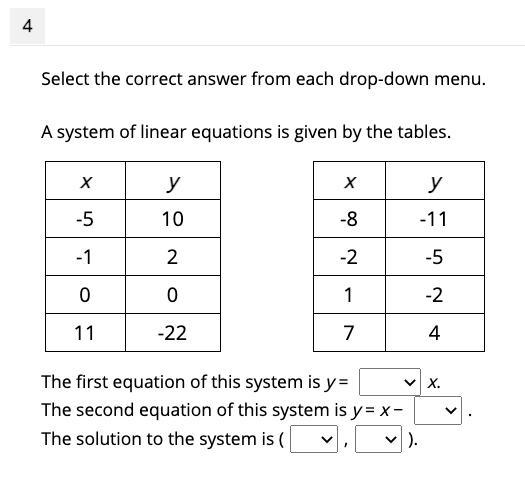
Answers
Answer:
equation 1
y = -2x
equation 2
y = x-3
Solution to both
(1,-2)
Step-by-step explanation:
We need to get the equations of both lines
General form is;
y = mx + c
where m is slope and c is the y-intercept
Table 1
since we have a point 0,0; the y-intercept here is zero
Let us get the slope. We can do this by selecting any two points
m = (y2-y1)/(x2-x1)
m = (2-10)/(-1+5) = -8/4 = -2
So the equation of the first line is;
y = -2x
Table 2
we get the slope
m = (4+2)/(7-1) = 6/6 = 1
The partial equation is;
y = x + c
To get c, we select any two point and substitute
4 = 7 + c
c = 4-7
c = -3
So the equation is;
y = x-3
To get the solution to both systems, we equate the y
-2x = x - 3
-2x-x = -3
-3x = -3
x = -3/-3
x = 1
To get y, we substitute;
recall; y = -2x
y = -2(1)
y = -2
Solution to the system is;
(1,-2)
l WILL GIVE BRAINLIEST......
find the range of X

Answers
Answer:
Step-by-step explanation:
Numbers that is less than 5 like 4,3,2,1,0
Answer:
1>x>-2 or -2<x<1
Step-by-step explanation:
2<3-x<5 (minus 3)
-1<-x<2 (devide by -1)
1>x>-2
How do I do the histogram

Answers
The histogram that represents this data-set is given at the end of the answer.
What is an histogram?An histogram is a graph that shows the number of times each element of x was observed.
When measures are spaced out, such as is the case in this problem, the bins of the histogram represent an interval of values. Hence, in this problem, we consider that:
6 measures are between 160 and 220.3 measures are between 220 and 280.4 measures are between 280 and 340.3 measures are between 340 and 400.2 measures are between 400 and 460.The histogram considering these intervals is given at the end of the answer.
More can be learned about histograms at https://brainly.com/question/25836450
#SPJ1

In order to determine an interval for the mean of a population with unknown standard deviation a sample of 61 items is selected. The mean of the sample is determined to be 23. The number of degrees of freedom for reading the t value is.
Answers
The number of degree of freedom for reading the t values is 60 , the correct option is (c) .
In the question ,
it is given that ,
number of items in the sample = 61 items
the mean of the sample is given as 23 ,
we have to find the degree of freedom(df) ,
the degree of freedom(df) can be solved using the formula
degree of freedom(df) \(=\) (number of observations) - 1
Substituting the values in the formula ,
we get ,
degree of freedom = 61 - 1
= 60
Therefore , The number of degree of freedom for reading the t values is 60 , the correct option is (c) .
The given question is incomplete , the complete question is
In order to determine an interval for the mean of a population with unknown standard deviation a sample of 61 items is selected. The mean of the sample is determined to be 23. The number of degrees of freedom for reading the t value is ?
(a) 22
(b) 23
(c) 60
(d) 61
Learn more about Degree Of Freedom here
https://brainly.com/question/22737637
#SPJ4
On a vertical line segment, point A is located at 50. Point B is located at 104. Point P is a point that divides segment AB in a ratio of 1:5 from A to B. Where is point P located?
Answers
Answer:
Step-by-step explanation:
Let the initial point on the line segment be O. If point A is located at 50 and point B is located at 104, then OA = 50 and OB = 104. Using the vector notation;
AO+OB = AB
(-OA)+OB = AB
-50+104 = AB
AB = 54
If point P divides the segment AB in a ratio 1:5, them AP:PB = 1:5
AP = 54/6
AP = 9
PB = 54-9
PB = 45
Hence the point P is located at 9 units from A and 45 units from B
PLEASE ANSWER ASAP! LOOK AT THE PIC ATTACHED: (please show work!)

Answers
Answer:
Answer is B
Step-by-step explanation:
Remember, perpendicular lines have opposite slopes. In order to do this, you just need to flip the sign (Change it to the opposite. For example, if it is 3, it would be -3), and change the slope to its reciprocal (For example, if it is 3, it would 1/3). Finally, since the equation is y = 1/2x + 10, the slope would change to -2x... so your answer is B
Can someone please help me woth this question...

Answers
Answer:
7£
Step-by-step explanation:
Shamus buys 2 adult tickets which are 24£, 3 children tickets which are 21£, and 1 senior ticket which is 8£. 24 + 21 + 8 is 53. If Shamus pays with three 20£ notes, he payed 60£ in total. Shamus only needs 53£ however. 60 - 53 is 7 so Shamus would get 7£ back as change.
the life of light bulbs is distributed normally. the variance of the lifetime is 625 and the mean lifetime of a bulb is 520 hours. find the probability of a bulb lasting for at most 549 hours. round your answer to four decimal places.
Answers
Light bulbs is normally distributed with a variance of 625 and a mean lifetime of 520 hours, we need to calculate the cumulative probability up to 549 hours. The answer will be rounded to four decimal places.
Given a normally distributed lifetime with a mean of 520 hours and a variance of 625, we can determine the standard deviation (σ) by taking the square root of the variance, which gives us σ = √625 = 25.
To find the probability of a bulb lasting for at most 549 hours, we need to calculate the area under the normal distribution curve up to 549 hours. This can be done by evaluating the cumulative distribution function (CDF) of the normal distribution at the value 549, using the mean (520) and standard deviation (25).
The CDF will give us the probability that a bulb lasts up to a certain point. Rounding the result to four decimal places will provide the desired precision.
Visit here to learn more about probability:
brainly.com/question/13604758
#SPJ11
The problem involves using normal distribution to find the probability of a given outcome. Using the Z-score, we can determine that the probability of a light bulb lasting for at most 549 hours is approximately 0.8770 or 87.70%
Explanation:Given the mean (µ) of the lifetime of a bulb is 520 hours. Also, the variance (σ²) is given as 625. Thus, the standard deviation (σ) is the square root of the variance, which is 25.
To find the probability of a bulb lasting for at most 549 hours, we first calculate the Z score. The Z-score formula is given as follows: Z = (X - µ) / σ, where X is the number of hours, which is 549. So substitute the given values into the formula. Z = (549 - 520) / 25, the Z value is 1.16.
We then look up the Z-table to find the probability associated with this Z-score (1.16), which is approximately 0.8770. Therefore, the probability of a bulb lasting for at most 549 hours is approximately 0.8770 or 87.70%.
Learn more about Probability here:https://brainly.com/question/32117953
#SPJ12
if necessary, how can a student determine the change in angular momentum δlδl of the cylinder from t=0t=0 to t=t0t=t0?
Answers
To determine the change in angular momentum (ΔL) of a cylinder from t = 0 to t = t0, a student can use the equation:
ΔL = I * Δω
where ΔL is the change in angular momentum, I is the moment of inertia of the cylinder, and Δω is the change in angular velocity.
To calculate Δω, the student needs to know the initial and final angular velocities, ω0 and ωt0, respectively. The change in angular velocity can be calculated as:
Δω = ωt0 - ω0
Once Δω is determined, the student can use the moment of inertia (I) of the cylinder to calculate ΔL using the equation mentioned earlier.
The moment of inertia (I) depends on the mass distribution and shape of the cylinder. For a solid cylinder rotating about its central axis, the moment of inertia is given by:
I = (1/2) * m * r^2
where m is the mass of the cylinder and r is the radius of the cylinder.
By substituting the known values for Δω and I into the equation ΔL = I * Δω, the student can calculate the change in angular momentum (ΔL) of the cylinder from t = 0 to t = t0.
It's important to note that this method assumes that no external torques act on the cylinder during the time interval. If there are external torques involved, the equation for ΔL would need to include those torques as well.
To learn more about angular momentum click here:
brainly.com/question/31592991
#SPJ11
THIS HAS MULTIPLE QUESTIONS PLEASE ANSWER ASAP
Question 1 Solve the inequality. |d + 2| ≥ 6
Question 2 Solve the equation. If there is no solution, select no solution. 5|x+3/4|=10
Question 3 Solve the inequality. –2 < 4 x – 10 < 6
Answers
Answer:
Question 1: d ≥ 4 or d ≤ -8
Step-by-step explanation:
Question 1 Solve the inequality. |d + 2| ≥ 6
d + 2 ≥ 6 or d + 2 ≤ -6
d ≥ 4 or d ≤ -8
One hundred people in your neighborhood always drive to work between 7:30 and 8:00 A.M. and arrive 30 minutes later. Why must two people always arrive at work at the same time, within a minute
Answers
Answer: Pigeonhole Principle
Step-by-step explanation:
The Pigeonhole Principle espouses that if there are more objects than the places the objects are supposed to fit into, some of those places will have more than one object. For instance, if there are 20 pigeons and only 19 pigeonholes, one pigeonhole will have more than one pigeon.
If one hundred people in your neighbourhood leave between 7:30 and 8:00 A.M. and arrive 30 minutes later that means they will arrive between 8:00 and 8:30 A.M. This means that 100 people will have to arrive in 30 minutes.
We would have to fit 100 people in 30 minutes. The minutes are the pigeonholes and the people are the pigeons. There will therefore be a situation where at least 2 people will arrive at the same minute because there are many more people than minutes for them to arrive in.
3. Consider the quadratic equation x2 + 2x - 35 = 0. Solve by factoring and using the zero-product property. What are solutions to quadratic equations called? Show your work.
Answers
Answer:
×=-2+12/2,the anwser is ×=5,×=-7
Michael is saving to buy his senior ring. The base cost of the ring is $280. There are also upgrades he can purchase for the ring. If he saves $35 each month, which solution represents how many months it will take Michael before he can purchase his ring?
Answers
Answer:
It will take him 8 months.
Step-by-step explanation:
If you divide 280 and 35 you get 8, which is the amount of months it takes.
What is the answer.”what is the slope and the y-intercept of the line on the graph below.

Answers
Answer: A: Slope = -4, y-intercept 1
Step-by-step explanation:
To find slope, do rise over run. The y-intercept is where the line crosses the y-axis.
\(3q + 2p + 7\)
Answers
5q+7
Explanation
3q+2q+7
Collect like terms by adding their coefficients
(3+2)q+7
Add the numbers
5x+7
12. Rewrite the expression in terms of the given function: (sec x + csc x)(sin x + cos x) - 2 - tan x; cotx O A. 2cot x B. cot x C. 2 + cotx D. 0
Answers
Answer: cot x
Step-by-step explanation:
(sec x + csc x)(sin x + cos x) - 2 - tan x >simplify to sin/cos
\(=(\frac{1}{cos x } +\frac{1}{sin x}) (sin x + cosx) -2-\frac{sinx}{cosx}\) >find common denominator
for first parenthesis
\(=(\frac{sinx+cosx}{sin xcos x }) (sin x + cosx) -2-\frac{sinx}{cosx}\) >Multiply the first 2
parenthesis
\(=(\frac{sin^{2} x+2sin x cos x+cos^{2} x}{sin xcos x }) -2-\frac{sinx}{cosx}\) >Use identity sin²x+cos²x=1
\(=(\frac{1 +2sin x cos x}{sin xcos x }) -2-\frac{sinx}{cosx}\) >Combine all fractions with
common denominator
\(=\frac{1 +2sin x cos x-2sinxcosx -sin^{2}x }{sin xcos x }\) >Simplify
\(=\frac{1 -sin^{2}x }{sin xcos x }\) >Use identity sin²x=1-cos²x
\(=\frac{1 -(1-cos^{2}x) }{sin xcos x }\) >Distribute negative
\(=\frac{1 -1+cos^{2}x }{sin xcos x }\) >simplify 1-1
\(=\frac{cos^{2}x }{sin xcos x }\) >simplify cos/cos
\(=\frac{cosx }{sin x }\) >Use identity cot=cos/sin
= cot x
Answer:
Option B, cotangent x or cot x
Step-by-step explanation:
First, I set up some shorthand based how each trig function operates in order to set up some conversion factors. You can also use trig identities if you are more familiar with those as the other answer suggests. That way is easier but it requires you to know the trig identities. If not, using the basic principles from angles of a right triangle can help:
Sine of x is the opposite leg over hypotenuse so we say S = O / H
Cosine of x is adjacent leg over hypotenuse so we say C = A / H
Tangent of x is opposite over hypotenuse so T = O / A
Cosecant of x is hypotenuse over opposite so csc = H / O
Secant of x is hypotenuse over adjacent so sec = H / A
Cotangent of x is adjacent over opposite so cot = A / O
For this first portion we are going to not think about the - 2 - tan x portion of the equation because we must FOIL the first part.
(sec x + csc x)(sin x + cos x)
FOIL stands for First, Outsides, Insides, and Lasts, marking what terms are multiply together in order to make an equation so:
Firsts: sec (sin x)
Outsides: sec (cos x)
Insides: csc (sin x)
Lasts csc (cos x)
So the new equation is:
sec (sin x) + sec (cos x) + csc (sin x) + csc (cos x)
Now we use our conversion factors to change each multiplication set:
\(\frac{H}{A}(\frac{O}{H}) + \frac{H}{A} (\frac{A}{H}) + \frac{H}{O}(\frac{O}{H}) + \frac{H}{O}(\frac{A}{H})\)
Use your knowledge of multiplying fractions and how variables in the numerator and denominator can cancel each other out. You simplify to:
\(\frac{O}{A} + 1 + 1 + \frac{A}{O}\)
Now use the conversion factors again to convert what is left into trig functions. O / A is tan x. A / O is cot x.
tan x + 2 + cot x.
NOW, bring back the portion we neglected earlier, simplify and solve.
tan x + 2 + cot x - 2 - tan x
tan x - tan x + 2 - 2 + cot x
0 + 0 + cot x
0 + cot x
cot x, option B
Slope
Rate Of Change
Pls Help

Answers
Answer:
-1/2
Step-by-step explanation:
HELPPPPPPPPPPPPPPPPPPPPPPP I"LLLL GIVE FIVE STAARS AND BRAINLIEST!!!!!!!!!!!!!!!
Figure 1- 6 blocks
figure 2- 11 blocks
Figure 3- 18 blocks
Which of the following functions represents f(n), the number of small squares in figure n?
a.f(n)=4n^2+2
b.f(n)=n^2+5
c.f(n)=(n+1)^2+2
d.f(n)=(n+1) (n+2)
Answers
Answer:
c. f(n) = (n+1)^2 + 2
Step-by-step explanation:
It is c. because...
f(n) = (1+1)^2 + 2
2^2 + 2
4 + 2 = 6 (first term)
f(n) = (2+1)^2 + 2
3^2 + 2
9 + 2 = 11 (second term)
f(n) = (3+1)^2 + 2
4^2 + 2
16 + 2 = 18 (third term)
if y is a positive integer, for how many different values of y is a whole number?
Answers
A positive integer y is a whole number by definition, so we are essentially being asked how many positive integers there are. There are infinitely many positive integers, so the answer to the question is also infinity.
A positive integer y is a whole number if it isn't a bit or a numeric. In other words, it's a number that can be expressed without using fragments or numbers, and can be written as a finite sum of positive integers. For illustration, 2, 5, and 10 are whole figures, but3/4,1.5, and √ 2 are not. To determine how numerous different values of y are whole figures, we need to understand the parcels of whole figures.
Whole figures have two main parcels they're closed under addition and addition. This means that when you add or multiply two whole figures, the result is always a whole number. For illustration, 2 3 = 5 and 2 × 3 = 6, both of which are whole figures. To find how numerous different values of y are whole figures, we can start with the lowest possible value of y, which is 1.
Learn more about whole numbers at
https://brainly.com/question/27934713
#SPJ1
what is the slope of the equation above?

Answers
Dhdjcusjbcjsjxjendxhdicisnchjd

Answers
Answer:
y=x+3
Step-by-step explanation:
slope is 1
intercept is 3
consider sequences that consist entirely of $a$'s and $b$'s and that have the property that every run of consecutive $a$'s has even length, and every run of consecutive $b$'s has odd length. examples of such sequences are $aa$, $b$, and $aabaa$, while $bbab$ is not such a sequence. how many such sequences have length 14?
Answers
The number of such sequences of strings of length 14 is 172.
Let \($a_n$\) and \($b_n$\) denote, the number of sequences of length n ending in A and B, respectively.
If a sequence ends in an A, then it must have been formed by appending two A's to the end of a string of length (n-2).
If a sequence ends in a B, it must have either been formed by appending one Bs to a string of length (n-1) ending in an A, or by appending two Bs to a string of length (n-2) ending in a B.
Thus, we get the recursions as follows -
\(a_n &= a_{n-2} + b_{n-2}\)
\(b_n &= a_{n-1} + b_{n-2}\)
By counting further, we find that \($a_1\)= 0, \(b_1\) = 1, \(a_2\) = 1, \(b_2\) = 0.
Similarly, we will get the following table -
Therefore, the number of such strings of length 14 is \($a_{14} + b_{14}\) = 80 + 92 = 172.
Read more about sequences:
brainly.com/question/6561461
#SPJ4
