Which do you think would have a higher value if c and d are positive decimal numbers:
4c + 2d or 6c + 3d? How can you be sure?
Answers
we can be sure that 6c + 3d will have a higher value than 4c + 2d if c and d are positive decimal numbers.
Explain variableA variable in mathematics is a symbol or letter that is used to indicate a quantity in a mathematical statement or equation that can have many values. It is a symbol that may be used to represent an arbitrary or undefined integer in algebraic expressions and equations.
Both expressions have the same common factor of 2, so we can simplify them as follows:
4c + 2d = 2(2c + d)
6c + 3d = 3(2c + d)
Since c and d are positive decimal numbers, we know that both 2c + d and 3(2c + d) are positive. Therefore, the expression with the higher value will be the one with the larger coefficient, which is 3 in the second expression.
So, we can be sure that 6c + 3d will have a higher value than 4c + 2d if c and d are positive decimal numbers.
To know more about factor, visit:
https://brainly.com/question/28983916
#SPJ1
Related Questions
the area A, of a rectangle is 120x (exponent of 2)+78x-90 , and a length, l, of the rectangle is 12x=15. which of the following given width, W, of the rectangle?
A. 9x+4
B. 10x - 19
C. 10x-6
D. 8x -6
Answers
Obtain minimum SOP expressions for the following Boolean functions using K-maps. (a) F(F,X,Y,Z)=〉m(2,3,6,7,8,9,12,13)->md(0,415) (b) F(W,X,Y,Z)=2m(0,3,4,5,6,7,1 1,12,13,14,15)2md(2,8,9) (c) F(F,X, Y,Z) 0,2,5,7,8,10,13) +Σ"d(1,9,11)
Answers
Using K-maps, the minimum SOP expressions for the given Boolean functions are as follows:
(a) F(F,X,Y,Z) = Y'Z' + X'Z + XYZ' + XY
(b) F(W,X,Y,Z) = W'X' + W'Y'Z + WX'Y' + WXYZ'
(c) F(F,X,Y,Z) = X'Y'Z' + XZ' + XYZ' + X'YZ
(a) For the function F(F,X,Y,Z), we create a K-map with variables X, Y, and Z as inputs and F as the output. By grouping adjacent 1s, we find that the minimum SOP expression is Y'Z' + X'Z + XYZ' + XY.
(b) For the function F(W,X,Y,Z), we create a K-map with variables W, X, Y, and Z as inputs and F as the output. By grouping adjacent 1s, we find that the minimum SOP expression is W'X' + W'Y'Z + WX'Y' + WXYZ'.
(c) For the function F(F,X,Y,Z), we create a K-map with variables X, Y, and Z as inputs and F as the output. By grouping adjacent 1s, we find that the minimum SOP expression is X'Y'Z' + XZ' + XYZ' + X'YZ.
The K-maps help visualize the simplification process by identifying adjacent 1s and creating groups based on their positions. The resulting SOP expressions provide simplified representations of the original Boolean functions.
Learn more about variables here:
https://brainly.com/question/29583350
#SPJ11
Please answer both ASAP I am stuck

Answers
Answer:
1st question: BD=88
2nd question: AB=24
Step-by-step explanation:
1st question:
BD is the total length (7x-10) which is equal to BC+CD [(4x-29)+(5x-9)]
so we have:
7x-10=9x-38
28=2x
x=14
BC= 4*14-29=27
CD= 5*14-9=61
BD=88
2nd question:
Since BD=BC
5x-26=2x+1
3x=27
x=9
AC=BC+AB
BC=2*9+1=18+1=19
43=19+AB
AB=24
Why did the National Assembly break away from the Estates General?
Answers
After Louis XVI's failed attempts to sabotage the Assembly and to keep the three estates separate, the Estates-General ceased to exist, becoming the National Assembly. It renamed itself the National Constituent Assembly on July 9 and began to function as a governing body and constitution-drafter.
National assembly
The National Assembly was the first revolutionary government of the French Revolution and existed from June 14th to July 9th in 1789. The National Assembly was created amidst the turmoil of the Estates-General that Louis XVI called in 1789 to deal with the looming economic crisis in France.
Learn more about National assembly here : -
https://brainly.com/question/9891529
#SPJ4
Ill give stars if correct.

Answers
Because 30 divided by 4
the question is on the picture

Answers
The length of the line segment is given by the distance equation
D = 7.2 units
What is the distance of a line between 2 points?The distance of a line between 2 points is always positive and given by the formula
Let the first point be A ( x₁ , y₁ ) and the second point be B ( x₂ , y₂ )
The distance between A and B is D , and the distance D is
Distance D = √ ( x₂ - x₁ )² + ( y₂ - y₁ )²
Given data ,
Let the distance of the line segment between two points be D
Now , the equation will be
Let the first point be represented as P ( 1 , 6 )
Let the second point be represented as Q ( 7 , 2 )
Now , distance between P and Q is D , and the distance D is
Distance D = √ ( x₂ - x₁ )² + ( y₂ - y₁ )²
D = √ ( 1 - 7 )² + ( 6 - 2 )²
On simplifying the equation , we get
D = √ ( -6 )² + ( 4 )²
D = √ ( 36 + 16 )
D = √ 52
D = 7.2 units
Hence , the distance is 7.2 units
To learn more about distance between 2 points click :
https://brainly.com/question/18234495
#SPJ1
is the integer k divisible by 4 ? (1) 8k is divisible by 16. (2) 9k is divisible by 12.
Answers
Yes , the integer k is divisible by 4 and statement (1) alone is sufficient to determine that k is divisible by 4.
Given data ,
Let the equation be represented as A
Now , the value of A is
a)
To determine if the integer k is divisible by 4, let's analyze the given statements:
Statement (1): 8k is divisible by 16.
This means that 8k is a multiple of 16. Since 16 is divisible by 4, we can conclude that k must be divisible by 4 as well. Therefore, statement (1) alone is sufficient to determine that k is divisible by 4.
8k = 16
k = 2
b)
This statement does not provide direct information about the divisibility of k by 4. While 12 is divisible by 4, the fact that 9k is divisible by 12 does not guarantee that k itself is divisible by 4.
9k = 12
k = 12/9
k = 4/3
So , it is not an integer
In conclusion, statement (1) alone is sufficient to determine that k is divisible by 4. Statement (2) is not sufficient on its own.
Click here to learn more about equations.
https://brainly.com/question/19297665
#SPJ1
Suppose that the distribution of a set of scores has a mean of 47 and a standard deviation of 14. if 4 is added to each score, what will be the mean and the standard deviation of the distribution of?
Answers
The new standard deviation of the distribution of X + 4 is also 14, for the given mean of 47 and standard deviation of 14.
Given:
Mean = 47
Standard deviation = 14
Adding 4 to each score, we get the new set of scores.
Let X be a random variable which represents the scores.
So the new set of scores will be X + 4.
Now,
Mean of X + 4 = Mean of X + Mean of 4
Therefore,
Mean of X + 4
= 47 + 4
= 51
So, the new mean of the distribution of X + 4 is 51.
Now, we will find the new standard deviation.
Standard deviation of X + 4 = Standard deviation of X
Since we have only added a constant 4 to each score, the shape of the distribution remains the same.
Hence the standard deviation will remain the same.
Know more about the standard deviation
https://brainly.com/question/475676
#SPJ11
1. Find the measure of y.
110°
z
yº
100°
87°
Answers
Answer:
97.8263768112
Step-by-step explanation:
Geometric Mean is denoted as 'x'
x = √(110×87)
x = √9570
∴ x = 97.8263768112
Define Geometric MeanThe Geometric Mean (GM) in mathematics is the average value or mean that, by calculating the product of the values of the set of numbers, denotes the central tendency of the numbers. In essence, we multiply the numbers together and calculate their nth root, where n is the total number of data values. For instance, the geometric mean for a given pair of numbers, say 3 and 1, is equivalent to (3 + 1) = 3 = 1.732.In other terms, the geometric mean is the product of n numbers divided by the nth root. The geometric mean differs from the arithmetic mean, as is noted. As a result of the fact that in arithmetic mean, the data values are added before being divided by the total number of values. However, when calculating the geometric mean, we multiply the provided data values before taking the root of the entire number of data values using the radical index. Take the square root, for instance, if there are two data points, the cube root if there are three, the fourth root if there are four, and so on.To learn more about Geometric Mean refer https://brainly.com/question/28347817
#SPJ1
7) Determine if the polynomials below are in the point polynomial time Justynach an! (points ==-+ 2022 in Riel (b) 3 points / 20021011.101 +2022 in C[x]. (c) 3 points] /= x+ 2022 in F7649[*] (Note that 7649 is prime. (d) pon-2 +3 in (e) [4 points] / -6° - 21x + 700 in Q[*]. (f) 14 points) f = 625x3 - 6633r2 + 86- 8855 in Qlur).
Answers
Let us check the given polynomials for point polynomial time as follows:
(a) Justynach an! (points ==-+ 2022 in Riel) This polynomial is not in point polynomial time because there is no condition on the polynomial and points.
(b) 3 points / 20021011.101 +2022 in C[x] This polynomial is not in point polynomial time because the given points are not on the polynomial.
(c) /= x+ 2022 in F7649[*] This polynomial is in point polynomial time because it is a monic polynomial and the given point is on the polynomial.
(d) pon-2 +3 This polynomial is not in point polynomial time because it is a constant polynomial and there are no points to verify.
(e) [4 points] / -6° - 21x + 700 in Q[*] This polynomial is in point polynomial time because all the points are on the polynomial.
(f) f = 625x3 - 6633r2 + 86- 8855 in Qlur. This polynomial is in point polynomial time because all the points are on the polynomial.
To know more about polynomial refer to:
https://brainly.com/question/7693326
#SPJ11
the measures of position that divide a set of data into four equal parts are called
Answers
The measures of position that divide a set of data into four equal parts are called quartiles.
Quartiles are statistical measures that divide a dataset into four equal parts, each containing approximately 25% of the data. These quartiles are denoted as Q1, Q2, and Q3.
Q1, also known as the first quartile or the 25th percentile, represents the value below which 25% of the data falls. It splits the lowest 25% of the dataset from the rest.
Q2, also known as the second quartile or the 50th percentile, is the median of the dataset. It represents the value below which 50% of the data falls, dividing the dataset into two equal parts.
Q3, also known as the third quartile or the 75th percentile, represents the value below which 75% of the data falls. It separates the highest 25% of the dataset from the rest.
These quartiles are useful in analyzing the distribution and dispersion of data, providing insights into the spread and central tendency.
They are commonly used in box plots, where the box represents the interquartile range (IQR), which is the range between Q1 and Q3, while the line inside the box represents the median (Q2).
Know more about quartiles here:
https://brainly.com/question/28169373
#SPJ11
How many radians is -89 degrees
Answers
Answer:
-1.5533
Step-by-step explanation:
-89 degrees x Pi/180 degrees
=-0.49444444444Pi rad
=-1.5533430342 rad
Znnzbamamaksmsnsnnsnsnsshhsjsjdhdndndhdbndjdbdbd
Non linear??????????

Answers
Answer:
Yes. That is correct
Step-by-step explanation:
xxxxxxxxxxxxxxxxxxxxxx
Pls help me with this

Answers
Answer: Can I see the whole questions?
Step-by-step explanation:
if f'(x) = x^2/1 x^5 and f(1)=3 then f(4)
Answers
Therefore, the value of function f(4) is: f(4) = ln (1025^(1/5) * e^15 / 2) - ln 2^(1/5) ≈ 20.212.
We can solve this problem by integrating the given derivative to obtain the function f(x), and then evaluating f(4).
From the given derivative, we can see that f'(x) can be written as:
f'(x) = x^2 / (1 + x^5)
To find f(x), we integrate both sides of the equation with respect to x:
∫ f'(x) dx = ∫ x^2 / (1 + x^5) dx
Using substitution, let u = 1 + x^5, so that du/dx = 5x^4 and dx = du / (5x^4).
Substituting these into the integral, we get:
f(x) = ∫ f'(x) dx = ∫ x^2 / (1 + x^5) dx
= (1/5) ∫ 1/u du
= (1/5) ln|1 + x^5| + C
where C is the constant of integration.
To determine the value of C, we use the initial condition f(1) = 3. Substituting x = 1 and f(x) = 3 into the above expression for f(x), we get:
3 = (1/5) ln|1 + 1^5| + C
C = 3 - (1/5) ln 2
So the function f(x) is:
f(x) = (1/5) ln|1 + x^5| + 3 - (1/5) ln 2
To find f(4), we substitute x = 4 into the expression for f(x):
f(4) = (1/5) ln|1 + 4^5| + 3 - (1/5) ln 2
= (1/5) ln 1025 + 3 - (1/5) ln 2
= ln (1025^(1/5) * e^15 / 2) - ln 2^(1/5)
To know more about function,
https://brainly.com/question/28278690
#SPJ11
is 8:10 less or more than 13:15
Answers
Answer:
8:10 is LESS than 13:15
Step-by-step explanation:
8:10 = 80%
13:15 = 86.7%
The area of a square is (4x2 + 20x + 25) square units. determine the length of each side of the square by factoring the area expression completely. show your work.
Answers
The length of each side of the square is (2x + 5)² units.
To determine the length of each side of the square, we need to factor the given area expression completely. The area of a square is equal to the square of the length of its side.
Given area expression: 4x² + 20x + 25
To factor this expression, we look for two binomials that multiply together to give the original expression. The first and last terms are perfect squares, which suggests that the expression may be factored as a perfect square binomial.
The perfect square binomial is given by: (a + b)^2 = a² + 2ab + b²
a²= (2x)²= 4x²
b² = (5)² = 25
2ab = 2(2x)(5) = 20x
the factored expression:
4x² + 20x + 25 = (2x + 5)²
To know more about square, refer here:
https://brainly.com/question/17207963#
#SPJ11
Earth is approximately 9. 3 × 107 miles from the sun. Saturn is approximately 8. 87 × 108 miles from the sun. About how much farther is Saturn from the sun than Earth is? A. 7. 94 × 107 miles B. 7. 94 × 108 miles C. 4. 3 × 107 miles D. 4. 3 × 108 miles.
Answers
To solve the problem we must know about Scientific notations.
Scientific notationsThe way through which a very small or a very large number can be written in shorthand. In scientific notations when a number between 1 and 10s is multiplied by a power of 10.
For example, 6,500,000,000,000 can be written as 6.5 x 10^12.
Saturn is (7.94 x 10^8) miles far from the sun than the Earth.
ExplanationGiven to us
Earth is approximately 9. 3 × 10^7 miles from the sun. Saturn is approximately 8. 87 × 10^8 miles from the sun.If we travel from the sun towards Saturn then we will find earth in between therefore, the earth lies in between these two.
Distance between Saturn and the earthDistance between Saturn and the earth
= Distance between Saturn and the sun - Distance between the earth and the sun
= (8.87 x 10^8) - (9.3 x 10^7)
= (88.7 x 10^7) - (9.3 x 10^7)
= (88.7 - 9.3) x 10^7
= 79.4 x 10^7
= 7.94 x 10^8
Hence, Saturn is (7.94 x 10^8) miles far from the sun than the Earth.
Learn more about Scientific notations:
https://brainly.com/question/1740231
Find the area of the parallelogram with vertices k(2, 2, 1), l(2, 3, 3), m(6, 9, 3), and n(6, 8, 1).
Answers
Let \(\vec K,\vec L,\vec M,\vec N\) be vectors pointing the vertices K, L, M, and N, respectively.
The side KL is parallel to and has the same length as the vector
\(\vec L - \vec K = (2\,\vec\imath + 3\,\vec\jmath + 3\,\vec k) - (2\,\vec\imath+2\,\vec\jmath+\vec k) = \vec\jmath + 2\,\vec k\)
Similarly, the side KN is parallel and as long as
\(\vec N - \vec K = (6\,\vec\imath+8\,\vec\jmath+\vec k) - (2\,\vec\imath+2\,\vec\jmath+\vec k) = 4\,\vec\imath+6\,\vec\jmath\)
These vectors have magnitudes
\(\|\vec L - \vec K\| = \sqrt{0^2 + 1^2 + 2^2} = \sqrt5\)
\(\|\vec N - \vec K\| = \sqrt{4^2 + 6^2 + 0^2} = 2\sqrt{13}\)
and their dot product is
\((\vec L - \vec K) \cdot (\vec N - \vec K) = 0\cdot4 + 1\cdot6+1\cdot0 = 6\)
The parallelogram spanned by the vectors \(\vec L-\vec K\) and \(\vec N-\vec K\) has area equal to the magnitude of their cross product, for which we have the identity
\(\bigg\|(\vec L - \vec K) \times (\vec N - \vec K)\bigg\| = \|\vec L - \vec K\| \|\vec N - \vec K\| \sin(\theta) \\\\ \implies \text{area} = 2\sqrt{65} \, \sin(\theta)\)
where \(\theta\) is the angle between the sides KL and KN.
From the dot product identity, we have
\((\vec L - \vec K) \cdot (\vec N - \vec K) = \|\vec L - \vec K\| \|\vec N - \vec K\| \cos(\theta) \\\\ \implies 6 = 2\sqrt{65} \cos(\theta)\)
Then
\(\cos(\theta) = \dfrac3{\sqrt{65}} \implies \sin(\theta) = \sqrt{1-\cos^2(\theta)} = 2\sqrt{\dfrac{14}{65}} \\\\ \implies \text{area} = 2\sqrt{65} \cdot 2\sqrt{\dfrac{14}{65}} = \boxed{4\sqrt{14}}\)
To get the total number of iterations in a nested loop, add the number of iterations in the inner loop to the number of iterations in the outer loop.
True
False
Answers
It is False that by adding the number of inner loops , we get the total number of iterations.
A loop is defined as a segment of code that executes multiple times. Iteration refers to the process in which the code segment is executed once. One iteration refers to 1-time execution of a loop. A loop can undergo many iterations.
There are 3 types of iteration: tail-recursion, while loops, and for loops. We will use the task of reversing a list as an example to illustrate how different forms of iteration are related to each other and to recursion. A recursive implementation of reverse is given below.
To learn more about iteration of loops
brainly.com/question/14266710
#SPJ4
Pls help asap thx its about Operations with Exponents
7.
8.
9.
10.

Answers
Answer:
7. 2s^7
8. 2s^4/5s^2
9. 108s^9
10. h^7
Step-by-step explanation:
7) (2s^3)^4
= 2s^(3+4)
= 2s^7.
8) (2s^2/5s)^2
= (2s^4/5s^2)
= 2s^4/5s^2.
9) 3s^5 × 4s^-2 × 9s^6
= 12s^{5+(-2)} × 9s^6
= 12s^3 × 9s^6
= 108s^9.
10) h^5/h^-2
= h^{5-(-2)}
= h^7.
if it helps don't forget to like and mark me
34. The distance a spring will stretch varies directly with how much weight is attached to the spring. If a spring stretches 8 inches with 90 pounds attached, how far will it stretch with 55 pounds attached? Round to the nearest tenth an inch
Answers
Madelyn has a points card for a movie theater.
She receives 70 rewards points just for signing up.
She earns 4.5 points for each visit to the movie theater.
She needs 115 points for a free movie ticket.
How many visits must Madelyn make to earn a free movie ticket?
Answers
The number of visits that Madelyn needs to make to the movie theater to earn a free movie ticket would be= 10.
How to calculate the number of visits needed by Madelyn?The number of points that Madelyn received for just signing up with the movie theater = 70 points.
The number of points she earns for each visit = 4.5 points
The total number of points the she needs = 115 points.
Let the total visit she requires = n
That is;
70+4.5n = 115
4.5n = 115-70
4.5n = 40
n = 10
Learn more about addition here:
https://brainly.com/question/29793687
#SPJ1
https://lamar.schoolobjects.com/eduphoria_webcontrols/attachmentwriter.aspx?orgguid=9267358f-cea3-413e-9ad1-b591dccc7264&attid=fe4b0fa8-610f-4118-9330-307fd0edc9ba
Answers
Answer:
ok
Step-by-step explanation:
Craig is considering four loans. loan l has a nominal rate of 8.254%, compounded daily. loan m has a nominal rate of 8.474%, compounded weekly. loan n has a nominal rate of 8.533%, compounded monthly. loan o has a nominal rate of 8.604%, compounded yearly. which of these loans will offer craig the best effective interest rate? a. loan l b. loan m c. loan n d. loan o please select the best answer from the choices provided a b c d
Answers
The effective interest rate of the loan would be
In this case, we are given 4 options:
Loan L has a nominal rate of 8.254% compounded dailyLoan M has a nominal rate of 8.474% compounded weeklyLoan N has a nominal rate of 8.533% compounded monthlyLoan O has a nominal rate of 8.604% compounded yearlyThe formula of compounded interest rate is:
\(A = P (1+\frac{r}{n})^{nt}\)
Where:
A = amount, P = principal amount, r = interest rate, n = number of times interest rate compounded, t = time
Let’s assume the principal amount is $100 for 1 year
Loan L =
\(A = 100 (1+\frac{0.08254}{356})^{356x1}\)
A = $108.603
Loan M =
\(A = 100 (1+\frac{0.08474}{52})^{52x1}\)
A = $108.834
Loan N =
\(A = 100 (1+\frac{0.08533}{12})^{12x1}\)
A = $108.875
Loan O =
\(A = 100 (1+\frac{0.08604}{1})^{1x1}\)
A = $108.604
Therefore, the best effective interest rate for Craig is Loan L with nominal rate of 8.254% compounded daily.
To learn more about interest rate, click here:
https://brainly.com/question/29117355
#SPJ4
Layne rode his bike from Point A to B by using Cherry Street. How much further would his trip have been if he took Orange Drive and Peach Avenue instead?
37 yards
14 yards
8 yards
28 yards

Answers
Juliet's monthly entertainment expenses are $275. 00 and account for 12% of her income. She would like to reduce her entertainment spending to 8% of her income. Calculate her new monthly entertainment buget
Answers
Using her monthly income, Juliet's new monthly entertainment budget is approximately $183.33.
What is her new monthly entertainment budget?To calculate Juliet's new monthly entertainment budget, we need to find her total monthly income and then calculate 8% of that amount.
Let's assume her current monthly entertainment expenses, $275.00, account for 12% of her income. We can set up the following equation:
275 = 0.12 * income
To find her total monthly income, we can divide both sides of the equation by 0.12:
income = 275 / 0.12
income ≈ 2291.67
Now that we know her total monthly income is approximately $2291.67, we can calculate her new monthly entertainment budget by taking 8% of her income:
new budget = 0.08 * income
new budget = 0.08 * 2291.67
new budget ≈ $183.33
Learn more on monthly income here;
https://brainly.com/question/29198497
#SPJ1
In a class of 40 students the number who studied French is 10 more than the number who studied History if 8 studied both French and History find using a venn diagram the number who Studied [1] History [2] French only
Answers
Answer:
11 students studied history
21 students studied French
8 students studied both
Step-by-step explanation:
first you have to subtract the number of students who studied both classes.
40-8=32
this leaves you with 32 students to study either history or French.
we know 10 more students studied French than history so subtract that from the 32 students because we already know where they go.
32-10=22
we're left with 22 students that can be equally split between the 2 classes.
22/2=11
so there are 11 more students in each history and French.
but don't forget to add the 10 more students that we already knew were in the French class.
11+10=21
Has the marrying age of a man changed over the years? The United States Bureau of the Census takes a formal count of everyone in the U.S. every 10 years and has provided the following data that gives the median age of an American man at the time of his first marriage.
Year
1910
1920
1930
1940
1950
1960
1970
1980
1990
2000
Median Age
25.1
24.6
24.3
24.3
22.8
22.8
23.2
24.7
26.1
26.8
Determine the average rate of change in median age per year from 1930 to 1960.
a.
-0.5 years of age per year
b.
20 years of age per year
c.
-0.05 years of age per year
d.
+0.05 years of age per year
Answers
-0.05 is the average rate of change in median age per year from 1930 to 1960.
What is ratio?The ratio can be defined as the number that can be used to represent one quantity as a percentage of another. Only when the two numbers in a ratio have the same unit can they be compared. Ratios are used to compare two objects.
Given, a data set that gives the median age of an American man at the time of his first marriage.
Year Median age
1910 25.1
1920 24.6
1930 24.3
1940 24.3
1950 22.8
1960 22.8
1970 23.2
1980 24.7
1990 26.1
2000 26.8
The average rate of change from 1930 to 1960 = (-24.3 + 22.8) / (1960-1930)
The average rate of change from 1930 to 1960 = -0.05
Therefore, the average rate of change in median age per year from 1930 to 1960 is -0.05.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ1
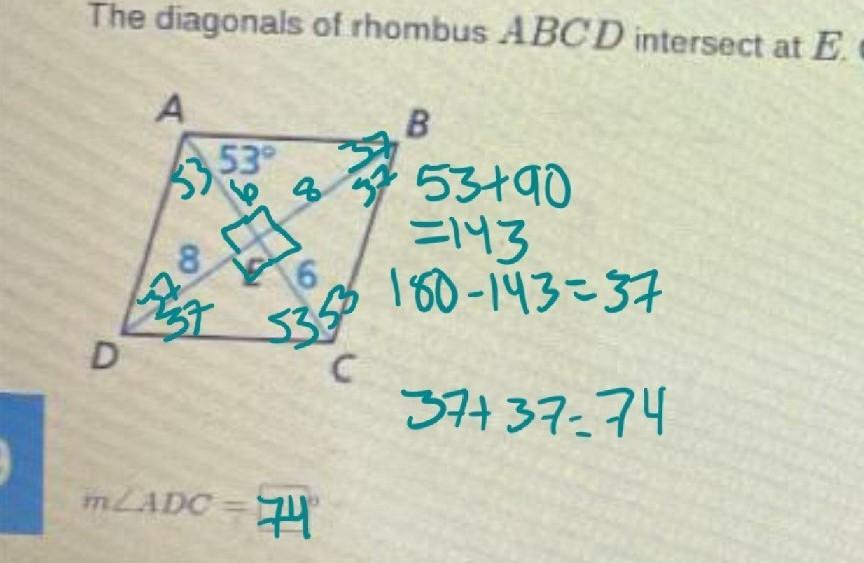
What is the measure of angle ADC?

Answers
angle ADC equals 74 degrees