where u get the 230,000 number

Answer:

54

Step-by-step explanation:

150/ 50 = 3

18 x 3 = 54

1.1) The volume of the cube is 27 cubic centimeters. 1.2)the density of the ice cube is approximately 0.917 grams per cubic centimeter (g/cm³).

1.3) the mass of the water cube is 27 grams. 1.4) the weight of the water and the ice would be the same under the same conditions. 1.5)In simpler terms, ice floats on water because it is lighter (less dense) than the water, allowing it to displace an amount of water equal to its weight and float on the surface.

1.1) The volume of the cube can be calculated using the equation: Volume = width x height x length. In this case, the cube measures 3 cm wide, 3 cm tall, and 3 cm long, so the volume is:

Volume = 3 cm x 3 cm x 3 cm = 27 cm³.

Therefore, the volume of the cube is 27 cubic centimeters.

1.2) Density is defined as mass divided by volume. The mass of the ice cube is given as 24.76 grams, and we already determined the volume to be 27 cm³. Therefore, the density of the ice cube is:

Density = Mass / Volume = 24.76 g / 27 cm³ ≈ 0.917 g/cm³.

Therefore, the density of the ice cube is approximately 0.917 grams per cubic centimeter (g/cm³).

1.3) The volume of the water cube is the same as the ice cube, which is 27 cm³. Given the density of liquid water as 1.00 g/cm³, we can calculate the mass of the water cube using the equation:

Mass = Density x Volume = 1.00 g/cm³ x 27 cm³ = 27 grams.

Therefore, the mass of the water cube is 27 grams.

1.4) The weight of an object depends on both its mass and the acceleration due to gravity. Since the volume of the water cube and the ice cube is the same (27 cm³), and the mass of the water cube (27 grams) is equal to the mass of the ice cube (24.76 grams), their weights would also be equal when measured in the same gravitational field.

Therefore, the weight of the water and the ice would be the same under the same conditions.

1.5) Ice floats on water because it is less dense than liquid water. The density of ice is lower than the density of water because the water molecules in the solid ice are arranged in a specific lattice structure with open spaces. This arrangement causes ice to have a lower density compared to liquid water, where the molecules are closer together.

When ice is placed in water, the denser water molecules exert an upward buoyant force on the less dense ice, causing it to float. The buoyant force is the result of the pressure difference between the top and bottom surfaces of the submerged object.

In simpler terms, ice floats on water because it is lighter (less dense) than the water, allowing it to displace an amount of water equal to its weight and float on the surface.

Learn more about cube;

brainly.com/question/15420947

#SPJ4

a) To graph the marginal utility of x, we need to find the derivative of the utility function with respect to x. Given that y=1, the utility function becomes U=x^(1/5). Taking the derivative of U with respect to x, we get dU/dx = (1/5)x^(-4/5). This represents the marginal utility of x.

When we graph the marginal utility of x, we put the marginal utility on the vertical axis and x on the horizontal axis. Since x^(-4/5) is positive for all positive values of x, the graph of the marginal utility of x will have a positive slope that decreases as x increases. The shape of the graph will resemble a downward-sloping curve that approaches zero as x approaches infinity.

b) The MRS (Marginal Rate of Substitution) for this consumer is the rate at which the consumer is willing to trade one good for another while keeping the total utility constant. In this case, the MRS is the negative ratio of the marginal utility of x to the marginal utility of y. Mathematically, MRS = -(dU/dx)/(dU/dy).

Since y is a constant and dU/dy = 0, the MRS simplifies to MRS = -(dU/dx)/0 = undefined. This means that the consumer is not willing to trade any amount of y for x, as the marginal utility of y is zero. The consumer only derives utility from x and does not value y in terms of marginal utility.

The graph of the marginal utility of x will have a positive slope that decreases as x increases. The MRS for this consumer is undefined, indicating that the consumer does not value y in terms of marginal utility.

To know more about marginal utility , visit ;

https://brainly.com/question/34280910

#SPJ11

Answer:

\(\frac{9+5\sqrt6}{23}\)

Step-by-step explanation:

We can rewrite the fraction as

\(\frac{2\sqrt{3}+3\sqrt{2}}{4\sqrt{3}+\sqrt{2}}\)

In order to rationalize the denominator of such a complex fraction, we must multiply the fraction by the conjugate of the denominator. In this case, the conjugate of the denominator would be \(4\sqrt{3}-\sqrt{2}\). Multiplying both sides of the fraction by the conjugate of the denominator would result in the fraction:

\(\frac{9+5\sqrt6}{23}\)

Answer:

\(12x\leq 24\); \(x\leq 2\)

Step-by-step explanation:

So you have 12 math problems that each take x amount of minutes, and have 24 minutes to finish them. Remember, you can't exceed the 24 minutes (but you are allowed to equal that time). So:

\(12x\leq 24\)

Then you can simplify by dividing both sides by 2:

\(x\leq 2\)

If PQ=RS, PQ=5x+9, and RS=x-31, then x=-10 can be proven by constructing two-column proof.

Given that PQ=RS, PQ=5x+9, and RS=x-31, we have to prove that x=-10. Let's construct a two-column proof to prove this.

Step 1: Write down the given information and the information to be proven.

Given: PQ=RS, PQ=5x+9, and RS=x-31To prove: x=-10

Step 2: Write down the reasons for each statement.                                          

 Given PQ = 5x+9                                            

 Given RS = x-31                                            

  Given 5x+9 = x-31                                        

 Substitution property 4x = -40                                                

Simplification x = -10                                                  

Division property of equality (Divide by 4)

Step 3: Write down the final statement that proves what we want to prove.x = -10    T

Therefore, PQ = RS = -10 + 31 = 21.

Learn more about division property from the given link

https://brainly.com/question/28749372

#SPJ11

First, we want to note two things:

We can describe this with an inequality:  x ≥ -10
Be sure you use ≥ and not >, since -10 is included.

We can describe this with interval notation: [ -10, infty )
Be sure you use [ and not ( on -10, since -10 is included.

You can also use set-builder notation: { x | x ≥ -10 }

Answer:

6

Step-by-step explanation:

10p-5/5 + 3(p-1) when p =2?

1)10(2)-5= 20-5= 15/5= 3

2) 3(2-1)=3(1)=3

3) 3+3=6

Answer:  See the image below.

Answer:

Step-by-step explanation:

o calculate the percent uncertainty, we need to divide the uncertainty (0.54 cm) by the measured value (23 m) and then multiply by 100 to get the percentage.

Step 1: Convert the measurement to a consistent unit. Since the uncertainly is given in centimeters (cm), we should convert the measured value from meters (m) to centimeters.

23 m = 23 * 100 cm = 2300 cm

Step 2: Calculate the percent uncertainty using the formula:

Percent Uncertainty = (Uncertainty / Measured Value) * 100

Percent Uncertainty = (0.54 cm / 2300 cm) * 100

Percent Uncertainty ≈ 0.02347826 * 100 ≈ 2.35%

Therefore, the percent uncertainty for the measuring tape is approximately 2.35%.

The cause-specific mortality rates per thousand for chronic conditions in the Bronx are (per thousand): Diabetes-related: 0.26,  Lung cancer: 0.44, Heart disease: 1.90 Asthma-related: 0.24.

To calculate the cause-specific mortality rate per thousand for chronic conditions in the Bronx, we divide the number of deaths from each specific condition by the total population and multiply by 1,000. By rounding the result to two decimal places, we can obtain the cause-specific mortality rate per thousand for each chronic condition of interest.

To calculate the cause-specific mortality rate per thousand for a particular chronic condition, we use the formula:

Mortality Rate = (Number of Deaths from the Condition / Total Population) * 1,000

Let's calculate the cause-specific mortality rates per thousand for each chronic condition based on the given figures:

Diabetes-related mortality rate:

(366 / 1,427,000) * 1,000 = 0.256 per thousand

Lung cancer mortality rate:

(633 / 1,427,000) * 1,000 = 0.443 per thousand

Heart disease mortality rate:

(2,711 / 1,427,000) * 1,000 = 1.898 per thousand

Asthma-related mortality rate:

(338 / 1,427,000) * 1,000 = 0.237 per thousand

Therefore, the cause-specific mortality rates per thousand for chronic conditions in the Bronx are approximately as follows:

Diabetes-related: 0.26 per thousand

Lung cancer: 0.44 per thousand

Heart disease: 1.90 per thousand

Asthma-related: 0.24 per thousand

These rates provide an indication of the number of deaths per thousand individuals in the population for each specific chronic condition of interest.

Learn more about decimal places here:

https://brainly.com/question/50455

#SPJ11

The value of x for the given equation is 16.

To find the value of x in the equation x + 10 = 26, we need to isolate x on one side of the equation by performing the same operation to both sides of the equation.

We can start by subtracting 10 from both sides of the equation:

x + 10 - 10 = 26 - 10

Simplifying the left-hand side gives:

x = 16

Therefore, the value of x is 16, as this is the solution that satisfies the equation x + 10 = 26.

Learn more about linear equation here: https://brainly.com/question/2030026
#SPJ1

The complete question is below:

Find the value of x: for x +10 = 26

The critical value for this two-tailed test is 2.6759.

To conduct a two-tailed test at the 0.01 level of significance with a sample of 55 observations, we use the t-distribution because the population standard deviation is unknown. The critical value is determined by dividing the significance level (0.01) by 2 to account for both tails of the distribution. This gives an alpha level of 0.005. Using the degrees of freedom for a sample of size 55 (54 degrees of freedom), we find the corresponding critical value from a t-distribution table or calculator. In this case, the critical value is approximately 2.6759 when rounded to four decimal places.Since the population standard deviation is unknown, we'll use the t-distribution instead of the standard normal distribution. The degrees of freedom for a sample of size 55 is 54. Using a t-distribution table or a statistical calculator, the critical value for an alpha level of 0.005 and 54 degrees of freedom is approximately 2.6759 (rounded to four decimal places).

learn more about two-tailed tests here:
https://brainly.com/question/8170655

#SPJ11

Answer: \(-2x^{2}+x+10\)

Step-by-step explanation:

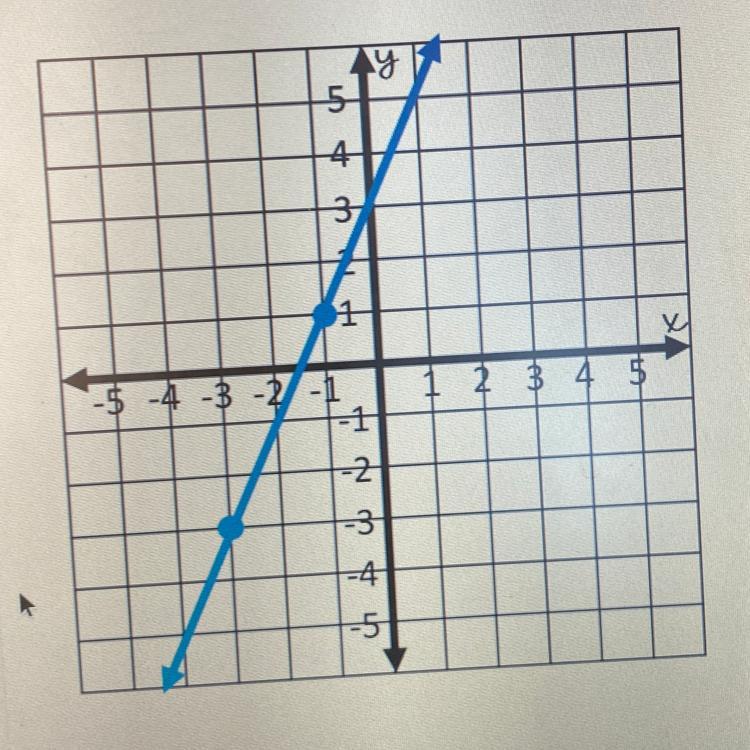
Answer:

slope is 4/2 or 2 if you're supposed to simplify.

Step-by-step explanation:

The line equation which models the data plotted on the graph is y = -16.67X + 1100

The equation for the line of best fit is expressed by the relation :

b = slope ; c = intercept

The slope , b = (change in Y/change in X)

Using the points : (28, 850) , (40, 650)

slope = (850 - 650) / (28 - 40)

slope = -16.67

The intercept is the point where the best fit line crosses the y-axis

Hence, intercept is 1100

Line of best fit equation :

Therefore , the equation of the line is y = -16.67X + 1100

Learn more on best fit : https://brainly.com/question/25987747

#SPJ1

the answer

155

324

5/9 (87/3(1/12)= 155/324

The price of a package of fruit bars are not proportional to the number of fruit bars in the package.

In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio, which is called the coefficient of proportionality or proportionality constant.

We are given that;

3 fruit bar = Rs 1.65

5 fruit bar= Rs 2.40

Now,

To determine whether the price of a package of fruit bars is proportional to the number of fruit bars in the package, we need to compare the unit prices of the two packages.

For the package of three fruit bars, the unit price can be found by dividing the total cost by the number of bars:

Unit price = 1.65 ÷ 3 = 0.55

For the package of five fruit bars, the unit price can be found in the same way:

Unit price = 2.40 ÷ 5 = 0.48

Since the unit prices are different, we can conclude that the price of a package of fruit bars is not proportional to the number of fruit bars in the package.

To know more about proportions visit;

brainly.com/question/24372153

#SPJ9

(-2, 5) Minimum

Step-by-step explanation:

y-5=(1/3)(x + 2)²

y-5=(1/3)(x²+4x+4))

y-5=1/3x²+4/3x+4/3

y=1/3x²+4/3x+4/3+5

y=1/3x²+4/3x+4/3+15/3

y=1/3x²+4/3x+19/3

graph is attached

x= -b/2a

x= (-4/3)/2(1/3)

x= (-4/3)/(2/3)

x= (-4/3)*(3/2)

3's cancel

x= (-4/1)*(1/2)

x = -4/2

x = -2

plug -2 back into

y=1/3x²+4/3x+19/3

y=1/3*4+4/3*-2+19/3

y=4/3-8/3+19/3

y=15/3

y=5

(-2,5)

if a is positive

graph looks like a smile

so minimum

if a is negative

graph looks like a frown

so maximum

quadraticswbi.weebly.com

Answer: 0.10

Step-by-step explanation:

Find the number in the hundredth place

9

9

and look one place to the right for the rounding digit

9

9

. Round up if this number is greater than or equal to

5

5

and round down if it is less than

5

5

.

0.10

Answer:

$368

Step-by-step explanation:

Well, if they pay their employees $10 per hour, and Tyrus worked 20 hours, then we have a base amount of 200, as 10*20=200. Next, we need to think about the 8% commission from 2100, so we multiply 2100*.92 to get 1932 so 2100-1932=168. So, to get the gross pay, you add the base amount, 200, and the commission, 168, together to get $368. Tyrus got a gross pay of 368 dollars last week.

Answer: Game 2.

Step-by-step explanation: The points double more than the last game by a lot, it's genuinely safe to say that game 2 solos enough to win over this entire argument.

Answer:

0.006

Step-by-step explanation:

0.6x0.005x0.02

Por lo tanto, pierde un total de 92 Bs.

Para averiguar la cantidad de dinero que un jugador de cartas pierde en total, debe calcular la suma de todas las ganancias y pérdidas.

El jugador de cartas comienza con 100 Bs, y luego gana 20 Bs.

Entonces, su cantidad total de dinero se convierte en

100 + 20 = 120 Bs.

Luego, pierde 35 Bs, lo que lo deja con

120 - 35 = 85 Bs.

Después de eso, pierde 52 Bs, y su saldo se convierte en

85 - 52 = 33 Bs.

Sin embargo, gana 75 Bs, por lo que su saldo aumenta a

33 + 75 = 108 Bs.

Luego pierde 115 Bs, lo que reduce su saldo a

108 - 115 = -7 Bs.

Finalmente, pierde 85 Bs, lo que significa que ha perdido un total de

-7 - 85 = -92 Bs.

Por lo tanto, el jugador pierde 92 Bs en total. En resumen, el jugador de cartas tiene 100 Bs al principio.

Luego gana 20 Bs, pierde 35 Bs, pierde 52 Bs, gana 75 Bs, pierde 115 Bs y pierde 85 Bs.

To learn more about Pierde :

https://brainly.com/question/23774082

#SPJ11

You're looking for "parabola" like shapes in which the lowest point has a y coordinate of y = 0. In this case, it would be the "parabola" portion on the right that has its lowest point at (3,0). The only interval that fits is \(2 \le x \le 4\) which in interval notation is written as [2,4]. So this fits with choice D.

The definite integral for the area of the surface generated by revolving the curve y = 6x^3 + 2x about the x-axis, over the interval 1 ≤ x ≤ 2, can be set up and evaluated as follows:

∫[1 to 2] 2πy √(1 + (dy/dx)^2) dx

To calculate dy/dx, we differentiate the given equation:

dy/dx = 18x^2 + 2

Substituting this back into the integral, we have:

∫[1 to 2] 2π(6x^3 + 2x) √(1 + (18x^2 + 2)^2) dx

Evaluating this definite integral will provide the surface area generated by revolving the curve about the x-axis.

b) The definite integral for the area of the surface generated by revolving the curve x = 4y - 1 about the y-axis, over the interval 1 ≤ y ≤ 4, can be set up and evaluated as follows:

∫[1 to 4] 2πx √(1 + (dx/dy)^2) dy

To calculate dx/dy, we differentiate the given equation:

dx/dy = 4

Substituting this back into the integral, we have:

∫[1 to 4] 2π(4y - 1) √(1 + 4^2) dy

Evaluating this definite integral will provide the surface area generated by revolving the curve about the y-axis.

By setting up and evaluating the definite integrals for the given curves, we can find the surface areas generated by revolving them about the respective axes. The integration process involves finding the appropriate differentials and applying the fundamental principles of calculus.

To know more about integral follow the link:

https://brainly.com/question/33191486

#SPJ11

To determine the number of roots of P(s) in the right half-plane, left half-plane, and on the jω-axis, we can use the Routh-Hurwitz stability criterion.

First, we construct the Routh array:

| 1 | 5 | 8 |

| 6 | 5 | 0 |

| -5.6 | 8 |

The first column of the Routh array has all positive elements, indicating that all the roots of the polynomial have positive real parts or are located on the jω-axis. However, the second column has one negative element, indicating that there is one root in the left half-plane.

To determine the number of roots on the jω-axis, we look for the number of sign changes in the first column of the Routh array. In this case, there is one sign change, indicating that there is one root on the jω-axis.

Therefore, the number of roots in the right half-plane is 0, the number of roots in the left half-plane is 1, and the number of roots on the jω-axis is 1.

The Routh array is a tabular method used in control engineering to determine the stability of a linear time-invariant system. It was introduced by Edward John Routh in the 19th century and is a valuable tool in analyzing the roots of a polynomial equation.

To construct a Routh array, the coefficients of the polynomial equation are arranged in a table, starting from the highest order term down to the constant term. The first two rows of the table are then calculated using the coefficients in the polynomial equation as follows:

Visit here to learn more about Routh array brainly.com/question/31318894

#SPJ11

The number of values in each group of the data set would be equal to the degrees of freedom for each group plus one.

In order to determine the number of values in each group of the data set based on the partially completed ANOVA table, we need to consider the total number of observations and the number of groups.

The ANOVA table consists of three main components: "Source of Variation," "Sum of Squares (SS)," and "Degrees of Freedom (df)." The "Source of Variation" represents the different factors or groups in the data set, while the "Sum of Squares" measures the variability within each group. The "Degrees of Freedom" represents the number of independent pieces of information available for estimating the population parameters.

In this case, since all groups are of the same size, we can determine the number of values in each group by examining the "Degrees of Freedom" column. The degrees of freedom for each group is the group size minus one (df = group size - 1). By adding one to the degrees of freedom for each group, we obtain the number of values in each group.

Learn more about ANOVA here:

https://brainly.com/question/30762844

#SPJ4

Answer:

250 miles

Step-by-step explanation:

The given distance between the house and the beach is 125 miles.

Let \(x\) miles be the distance between the house and the lunch stop.

So, at the time of the lunch stop, he already traveled \(x\) miles, the remaining distance is the distance between the lunch stop and the beach.

Let \(y\) miles be the remaining distance, so

\(y=125-x.\)

Give that the ratio of the distance he has traveled, \(x\), to the distance he still has to travel, \(y\), is \(2:3\),i.e

\(x:y=2:3\)

\(\Rightarrow \frac x y =\frac 2 3\)

\(\Rightarrow \frac {x}{125-x}=\frac 2 3\)

\(\Rightarrow 3\times x=2\times(125-x)\)

\(\Rightarrow 3\times x=2\times125-2\timesx\)

\(\Rightarrow 3 x=250-2x\)

\(\Rightarrow 3x-2x=250\)

\(\Rightarrow x=250\)

Hence, the distance traveled by Herman when he stops for lunch is 250 miles.