What is the z-score if u = 89, 0 = 11.5, and x = 82?O 1.370 -0.610.790 -1.21
Answers
The standard normal distribution (Z) is defined as the difference between the value of the variable, X, and the population mean, μ, and the result divided by the population standard deviation, σ.
\(Z=\frac{X-\mu}{\sigma}\approx N(0,1)\)For a determined population with normal distribution, the mean is μ=89, the standard deviation is σ=11.5 and the value of the variable is X=82, you can calculate the Z-value as follows:
\(\begin{gathered} Z=\frac{82-89}{11.5} \\ Z=\frac{-7}{11.5} \\ Z=-0.608\approx-0.61 \end{gathered}\)The Z-value is -0.61
Related Questions
Given the function h of x equals negative 2 times the square root of x, which statement is true about h(x)?The function is decreasing on the interval (0, [infinity]).The function is decreasing on the interval (–[infinity], 0).The function is increasing on the interval (0, [infinity]).The function is increasing on the interval (–[infinity], 0).
Answers
The function is decreasing on the interval (0, [infinity])
The function h of x equals negative 2 times the square root of x is a decreasing function on the interval (0, ∞). This means that as the value of x increases, the value of h(x) decreases. On the interval (-∞, 0), the function is increasing. This means that as the value of x decreases, the value of h(x) increases. The graph of the function looks like a parabola that opens downward and is symmetric around the y-axis. The graph is a concave down curve, and the y-intercept is at (0, 0). As the value of x gets closer to 0, h(x) approaches negative infinity. As x approaches infinity, h(x) approaches 0. This means that the range of h(x) is (-∞, 0].In order to determine if the function is increasing or decreasing on a given interval, we need to look at the sign of the derivative of the function on the interval.
The derivative of h(x) is -2/sqrt(x).
For the interval (0, [infinity]), the derivative of h(x) is negative, indicating that the function is decreasing.
For the interval (–[infinity], 0), the derivative of h(x) is positive, indicating that the function is increasing.
Learn more about confidence interval here
https://brainly.com/question/24131141
#SPJ4
Realiza las siguientes multiplicaciones
a) (+27) ⋅ (+2) =
b) (+12) ⋅ (−13) =
c) (−10) ⋅ (+10) =
d) (−56) ⋅ (+89) =
e) (−100) ⋅ (−135) =
f) (+553) ⋅ (+24) =
Answers
Answer:
A 54
b -156
c -100
d -4984
e 13500
f 13272
Approximately how many times greater is 374,000 than 22,000?
Answers
Answer:
352,000
Step-by-step explanation:
Subtract 374,000 by 22,000 and you will get 352,000 as your answer
The number 374000 is greater then 22000 by exactly 25200 amount.
What is mathematic expression?
A mathematical expression is defined as the collection of the numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
Here, to find out by how much times the number 374000 is greater then the number 22000 we simply subtract the number 374000 by 22000 which comes out be 35200.
It should be noted that, To cross verify the answer we can add 35200 with 22000 it must be equal to 374000.
374000 - 22000 = 352000
Therefore, the number 374000 is greater then 22000 by exactly 25200 amount.
Read more about addition here :
https://brainly.in/question/10133124
#SPJ2
What is the value of the expression below when x=6?

Answers
Answer:
2,622
Step-by-step explanation:
To determine the value of \( 2x^4 + 5x \) when x = 6, plug in the value of x, them evaluate.
\( 2(6)^4 + 5(6) \)
\( 2(1,296) + 30 \)
\( 2,592 + 30 \)
\( = 2,622 \)
What is the slope of the line that contains the points (-1,8) and (5,-4)?

Answers
Answer:
the answer would be D
Step-by-step explanation:
i worked it out and thats what i came to
Find the value of $10,000 in 10 years. The investment earns 8% for four years and then earns 4% for the remaining six years
Answers
Answer: After investing for 10 years at 8% interest
Step-by-step explanation: your $10,000 investment will have grown to $21,589 This calculator determines the future value of $10k invested for 10 years at a constant yield of 8.00% compounded annually
Analyze the graph of the function f(x) to complete the statement. On a coordinate plane, a curved line, labeled f of x, with a minimum value of (0, negative 3) and a maximum value of (negative 2.4, 17), crosses the x-axis at (negative 3, 0), (negative 1.1, 0), and (0.9, 0), and crosses the y-axis at (0, negative 3). f(x)<0 over and what other interval?
Answers
The interval where function f(x) is negative and greater than 0 is (-∞, -3) U (-1.1, 0)
We have,
The function f(x) crosses the x-axis at (-3, 0), (-1.1, 0), and (0.9, 0), it means that f(x) is negative for x values less than -3, between -1.1 and 0.9, and greater than 0.
Therefore, we can say that:
f(x) < 0 for x < -3 and -1.1 < x < 0.9
And,
The function f(x) has a minimum value of (0, -3) and a maximum value of (-2.4, 17).
This means that f(x) is positive for x values greater than -2.4. Therefore, we can say that:
f(x) > 0 for x > -2.4
Now,
Combining these inequalities, we can say that f(x) is negative over the intervals (-∞, -3) and (-1.1, 0.9), and positive over the interval (-2.4, ∞).
So,
The interval where f(x) is negative and greater than 0 is:
(-∞, -3) U (-1.1, 0)
Thus,
The interval where f(x) is negative and greater than 0 is (-∞, -3) U (-1.1, 0)
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
My question... please answer asap

Answers
Answer:
slope=1/4
y-intercept=3
y=.25x+3
Step-by-step explanation:
slope=rise over run so
slope=1/4
y-intercept is the value of y where the line crosses the y axis..
y-intercept=3
In y=mx+b form m is slope and b is y-intercept so...
y=.25x+3
A circle P is circumscribed about a regular hexagon ABCDEF
If segment AD is drawn, ADEF is a
Select one:
O a. rhombus
O b. rectangle
O c. trapezoid
O d. square
Answers
Answer:
C. Trapezoid
Step-by-step explanation:
A hexagon is a polygon with six sides, thus and six interior angles ABCDEF. After the segment AD (which is the diameter of the circle P) has been drawn, it divides the hexagon into two halves. With each half forming the shape of a trapezoid, so that ADEF is a trapezoid.
Thus, the appropriate option is C, trapezoid.
in a right triangle ABCD prove that angle abc is equal to angle CAD
Answers
Question 13 FUNDRAISER Owen is organizing a fundraiser. The proceeds will be split between a charity and the expenses from the fundraiser. Owen would like the cost of the fundraiser to be 15% of the proceeds. If the fundraiser will cost $500, how much money do they need to raise at the fundraiser?
Answers
Answer:
The amount to be raised at the fund raiser is $3,333.33
Step-by-step explanation:
Here, we want to know the amount of money needed to be raised for the fundraiser
Let the amount raised be $x
Thus;
15% of $x = $500
$500 is the cost of the fund raiser
15/100 * x = 500
15x/100 = 500
15x = (100 * 500)
x = (100 * 500)/15
x = 3,333.33
The perimeter of a square is 56. Express the length of a diagonal of the square in simplest radical form.?
Answers
The length of the diagonal of a square with a perimeter of 56 is 14√2.
What is a diagonal?A diagonal is the longest line that divides a plane shape into two equal parts.
To calculate the length of the diagonal of the square, first we need to find the length of the square using the perimeter formula.
Formula:
P = 4a............ Equation 1Where:
P = Perimeter of the squarea = Length of the squareFrom the question,
Given:
P = 56Substitute the value into equation 1 and solve for a
56 = 4aa = 56/4a = 14Finally to find the length of the diagonal of the square, we use the formula below
d = √(2a²)................... Equation 2Where:
d = Lenght of the diagonal of the squarea = Length of the square = 14Substitute into equation 2
d = √(2×14²)d = 14√2Hence, the length of the diagonal is 14√2.
Learn more about diagonal here: https://brainly.com/question/27341413
#SPJ1
Answer:
qfewwqeffwqfefewqwqreg
Step-by-step explanation:
PLS HELP- A satellite can move at 17,000 miles per hour. How many hours will it take to reach a star that is three light years away? Recall that 1 light year = 9.5 ∙ 1012 kilometers and 1 kilometer = 0.62 miles. Show your work.
Answers
Answer:
3.465 x 10⁸ hours
or
346,500,000 hours
Step-by-step explanation:
Distance to travel to star = 9.5 x 10¹² kilometers
1 kilometer = 0.62mile
Therefore
9.5 x 10¹² km = 9.5 x x 10¹ x 0.6 miles
= 5.89 x 10¹² miles
Speed of satellite = 17,000 mph
In scientific notation
17,000 = 17 x 10³ = 1.7 x 10⁴ mph
Time taken to reach star at distance of 5.89 x 10¹² miles
= 5.89 x 10¹² miles/1.7 x 10⁴ mph = 5.89/1.7 x 10¹²/10⁴
= 3.465 x 10¹²⁻⁴
= 3.465 x 10⁸ hours
= 346,500,000 hours
Please answer and explain fully thank you

Answers
Answer:
Therefore, the roots of the given equation are x = 2, x = 1, and x = -3.
Step-by-step explanation:
This problem involves finding the zeros (or roots) of a polynomial equation, which are the values of x that make the equation equal to zero. The given equation is cubic, meaning it has a degree of 3 and can have up to three real roots.
One way to find the roots of this equation is to use the Rational Root Theorem, which states that any rational root of a polynomial equation with integer coefficients must have the form p/q, where p is a factor of the constant term (in this case 18) and q is a factor of the leading coefficient (in this case 3). However, this method only works for finding rational roots, and there may be irrational or complex roots as well.
Another method is to use a graphing calculator or software to graph the equation and visually locate the x-intercepts, which are the points where the graph crosses the x-axis and the value of y is zero. From the graph, we can see that there are three real roots: one positive, one negative, and one between -2 and -1.
A third method is to use numerical methods (such as Newton's method or the Bisection method) to estimate the roots to a desired level of accuracy. However, this method involves iterative calculations and can be time-consuming.
Without using a graphing calculator, we can try to factor the given equation by using the Rational Root Theorem. The possible rational roots are ±1, ±2, ±3, ±6, ±9, ±18 (all factors of 18 divided by all factors of 3). We can test these roots by substituting them into the equation and seeing if the result equals zero.
Testing x = 1 gives:
3(1)^3 - 2(1)^2 - 13(1) + 18 = 3 - 2 - 13 + 18 = 6, which is not zero.
Testing x = -1 gives:
3(-1)^3 - 2(-1)^2 - 13(-1) + 18 = -3 - 2 + 13 + 18 = 26, which is not zero.
Testing x = 2 gives:
3(2)^3 - 2(2)^2 - 13(2) + 18 = 3(8) - 2(4) - 13(2) + 18 = 0, which means x = 2 is a root.
Using polynomial division, we can factor out (x - 2) from the cubic polynomial to obtain a quadratic polynomial that can be factored:
(3x^3 - 2x^2 - 13x + 18) / (x - 2) = 3x^2 + 4x - 9
Factoring the quadratic gives:
3x^2 + 4x - 9 = (3x - 3)(x + 3)
Setting each factor equal to zero and solving for x gives:
3x - 3 = 0, so x = 1
x + 3 = 0, so x = -3
Help me please 10 pointsssss

Answers
Answer:
I think it may be a but I am not completely sure
Step-by-step explanation:
X = -1/2 , 3
Since it’s asking for the length, X would not be negative.
RS = 4X = 4*3 = 12
Two turtles, Velma and Justine, were entered into a race.
The equation y = 4x represents Velma's distance in meters, y, after racing for x minutes. The graph below displays Justine's distance and time.
Based on the equation and graph, which two statements below are true?
A.Justine is twice as fast as Velma.
B. Justine is half as fast as Velma.
C. Justine and Velma have the same speed.
D. Justine moves a greater distance than Velma each minute.
E. Justine moves a shorter distance than Velma each minute.

Answers
Answer:
B and E
Step-by-step explanation:
the graph (Justine) shows the line
y = 2x
the line for Velma is
y = 4x
now we need to remember that the slope (inclination) of a line is the factor of x (so, 2 and 4 in the two line equations).
a slope is expressed as y/x and indicates how many units y changes when x changes a certain amount of units (like 1).
as described (and also confirmed by the graph) the x units are minutes, and the y units are meters.
so, as per her slope, Velma moves 4 meters in 1 minute.
and Justine moves 2 meters in 1 meter.
so, Justine is half as fast as Velma.
and therefore, Justine moves a shorter distance than Velma each minute.
Answer:
Step-by-step explanation:
B and E
Find the missing side length.
Assume that all intersecting sides meet at right angles.
Be sure to include the correct unit in your answer.
13 ft
5 ft
?
9 ft
6 ft
4 ft

Answers
The measure of the missing side length from the given figure is 11 feet.
What is right angle?The right angle is created when two straight lines cross at a 90° angle or when they are perpendicular at the intersection.
It is referred to as a right angle if the angle formed by two rays exactly equals 90 degrees, or π/2.
The adjacent angles are right angles if a ray is positioned so that its terminus is on a line and they are equal.
In the given figure, assuming that all the intersecting sides meet at right angles.
So, the opposite sides are parallel to each other.
Let x be the length of missing side.
Thus, The length of missing side = Sum of length of parallel sides
Now, x= 5+6
= 11 feet
Therefore, the length of side missing is 11 feet.
To learn more about the right angle visit:
https://brainly.com/question/3770177.
#SPJ1

Eugene and Jessica each improved their yards by planting hostas and geraniums. They bought
their supplies from the same store. Eugene spent $150 on 18 hostas and 6 geraniums. Jessica
spent $113 on 7 hostas and 16 geraniums. Find the cost of one hosta and the cost of one
geranium.
Answers
The cost of one hosta is approximately $7 and the cost of one geranium is approximately $4.
To find the cost of one hosta and one geranium, we can set up a system of equations based on the given information.
Let's assume the cost of one hosta is represented by 'h' and the cost of one geranium is represented by 'g'.
From the information given, we can set up the following equations:
Eugene's spending:
18h + 6g = $150
Jessica's spending:
7h + 16g = $113
We can now solve this system of equations to find the values of 'h' and 'g'.
Multiplying the first equation by 2 and the second equation by 3 to eliminate 'g', we get:
36h + 12g = $300
21h + 48g = $339
Now, we can subtract the second equation from the first to eliminate 'h':
(36h + 12g) - (21h + 48g) = $300 - $339
36h - 21h + 12g - 48g = -$39
15h - 36g = -$39
Simplifying further, we have:
15h - 36g = -$39
Now we can solve this equation for 'h' and substitute the value back into any of the original equations to find 'g'.
Let's solve for 'h':
15h = 36g - $39
h = (36g - $39) / 15
Substituting this value of 'h' into Eugene's equation:
18[(36g - $39) / 15] + 6g = $150
(648g - $702) / 15 + 6g = $150
648g - $702 + 90g = $150 * 15
738g - $702 = $2250
738g = $2250 + $702
738g = $2952
g = $2952 / 738
g ≈ $4
Now, substituting the value of 'g' back into Eugene's equation:
18h + 6($4) = $150
18h + $24 = $150
18h = $150 - $24
18h = $126
h = $126 / 18
h ≈ $7
Therefore, the cost of one hosta is approximately $7 and the cost of one geranium is approximately $4.
For such more questions on Cost of Hosta & Geraniums
https://brainly.com/question/14324591
#SPJ8
Write an equation of the line in point-slope form that passes through the given points.
(4,4) and (5,7)
Please explain answer
Answers
Answer: y-4 = 3(x - 5)
Step-by-step explanation:
The basic form for a point-slope equation is
y - b = m(x - a)
a is the x-value from the given coordinate, b is the y-value form the given coordinate, m is the slope. x and y are the variables in the function.
To find the slope, m, use the given coordinates. Get the difference in the y-values and divide by the difference in the x-values. This is "rise over run."
Given coordinate points: (4,4) and (5,7) \(m=\frac{y-y_{1} } {x-x_{1 }}\) substitute values:
m= 7-4/5-4 becomes m= 3/1 so the slope m = 3
To write the equation: Take the basic form, substitute b and a values from either given coordinate. And use the value of m we just calculated.
y - b = m(x - a) Using the second coordinate: (5,7)
y - 7 = 3(x - 5)
The attachment shows the graph of this equation.
(The equivalent slope-intercept form for this is y = 3x - 8 )

Answer:
Y - 4 = 3(X - 4)
Step-by-step explanation:
Y2 - Y1 / X2 - X1 = M, 7 - 4 / 5 - 4 = M, 3 / 1 = M, M = 3
Y - Y1 = M(X - X1),
Y - 4 = 3(X - 4),
Y - 4 = 3X - 12,
+4 +4
Y = 3X - 8
This data is from a sample. Calculate the mean, standard deviation, and variance. Suggestion: use technology. Round answers to two decimal places.
x
22.8
49.8
17.5
44.1
33.2
20.6
43.2
37.7
Mean =
Standard Deviation =
Variance =
Ooops - now you discover that the data was actually from a population! So now you must give the population standard deviation.
Population Standard Deviation =
Answers
1. Mean = 33.61
2. Standard Deviation = 11.3284
3. Variance = 128.33
What are the mean, standard deviation, and variance?The given data are: \(22.8, 49.8, 17.5, 44.1, 33.2, 20.6, 43.2, 37.7\)
To get mean, we will sum up all the numbers and divide by the total count. The mean is:
= (22.8 + 49.8 + 17.5 + 44.1 + 33.2 + 20.6 + 43.2 + 37.7) / 8
= 268.9 / 8
= 33.62
Standard Deviation: \(\sqrt((22.8 - 33.61)^2 + (49.8 - 33.61)^2 + (17.5 - 33.61)^2 + (44.1 - 33.61)^2 + (33.2 - 33.61)^2 + (20.6 - 33.61)^2 + (43.2 - 33.61)^2 + (37.7 - 33.61)^2) / 8\)
= \(\sqrt{128.3336}\)
= 11.3284420818
= 11.3284
Variance = (Standard Deviation)^2
Variance = \(11.3284 ^2\)
Variance = 128.33264656
Variance = 128.33.
Read more about measure of centres
brainly.com/question/15214370
#SPJ1
(4a-5)-(-2a-3) find the difference
Answers
Answer: \(6a-2\)
Step-by-step explanation:
\((4a-5)-(-2a-3)\\=4a-5+2a+3\\=6a-2\)
The difference of (4a-5)-(-2a-3) is 64a^15 = 9a is different to 5
Apply the product rule to 4a^5:
⇒ 4^3(a^5)^3
Raise 4 to the power of 3:
⇒ 64(a^5)^3
Apply the power rule and multiply exponents, (a^m)^n = a^mn:
⇒ 64a^5*3
Multiply 5 by 3:
64a^15
⇒ (4a-5)⇒ = 9a⇒ (-2a-3)⇒ = 5Therefore, The difference of (4a-5)-(-2a-3) is 64a^15 = 9a is different to 5
#SPJ3
Pre - Calculus evaluate exponential derivative at a point !

Answers
Answer:
\(\displaystyle\)\(\displaystyle f'(1)=-\frac{9}{e^3}\)
Step-by-step explanation:
Use Quotient Rule to find f'(x)
\(\displaystyle f(x)=\frac{3x^2+2}{e^{3x}}\\\\f'(x)=\frac{e^{3x}(6x)-(3x^2+2)(3e^{3x})}{(e^{3x})^2}\\\\f'(x)=\frac{6xe^{3x}-(9x^2+6)(e^{3x})}{e^{6x}}\\\\f'(x)=\frac{6x-(9x^2+6)}{e^{3x}}\\\\f'(x)=\frac{-9x^2+6x-6}{e^{3x}}\)
Find f'(1) using f'(x)
\(\displaystyle f'(1)=\frac{-9(1)^2+6(1)-6}{e^{3(1)}}\\\\f'(1)=\frac{-9+6-6}{e^3}\\\\f'(1)=\frac{-9}{e^3}\)
Answer:
\(f'(1)=-\dfrac{9}{e^{3}}\)
Step-by-step explanation:
Given rational function:
\(f(x)=\dfrac{3x^2+2}{e^{3x}}\)
To find the value of f'(1), we first need to differentiate the rational function to find f'(x). To do this, we can use the quotient rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $f(x)=\dfrac{g(x)}{h(x)}$ then:\\\\\\$f'(x)=\dfrac{h(x) g'(x)-g(x)h'(x)}{(h(x))^2}$\\\end{minipage}}\)
\(\textsf{Let}\;g(x)=3x^2+2 \implies g'(x)=6x\)
\(\textsf{Let}\;h(x)=e^{3x} \implies h'(x)=3e^{3x}\)
Therefore:
\(f'(x)=\dfrac{e^{3x} \cdot 6x -(3x^2+2) \cdot 3e^{3x}}{\left(e^{3x}\right)^2}\)
\(f'(x)=\dfrac{6x -(3x^2+2) \cdot 3}{e^{3x}}\)
\(f'(x)=\dfrac{6x -9x^2-6}{e^{3x}}\)
To find f'(1), substitute x = 1 into f'(x):
\(f'(1)=\dfrac{6(1) -9(1)^2-6}{e^{3(1)}}\)
\(f'(1)=\dfrac{6 -9-6}{e^{3}}\)
\(f'(1)=-\dfrac{9}{e^{3}}\)
Find the value of x.

Answers
Answer:
6 .x = 121°
Sum of all interior angles of a 7 sided polygon is 900°.
I'll Give brainliest to whoever answers is correct
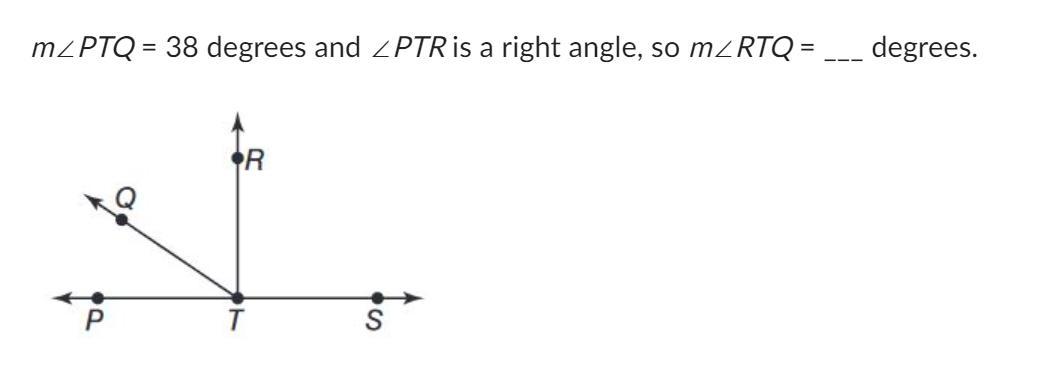
Answers
Answer:
52
Step-by-step explanation:
RTQ is 52 because if PTR is a right angle, right angles equal 90 degrees. So if PTQ is 38 degrees, we subtract 38 from 90 to get RTQ. 90-38 equals 52.
Answer:
52 degrees
Step-by-step explanation:
right angle = 90
90-38=52
So RTQ = 52 degrees
Round the number to the nearest hundred-thousandth 2.95632694
Answers
i pretty dumb and i really don’t know math haha..

Answers
\({x}^{ log_{3}(x) } = 81 {x}^{3} \)
can you solve by algebraically, not graphing and provide step by step explanation, please?
Answers
Answer:
x=81 or 1/3
Step-by-step explanation:
\(x^\log_3(x)} =81x^3\\\log_3(x^{\log_3(x)})=\log_3(81x^3)\\\(\log_3x)(\log_3x)=\log_381+\log_3x^3\\(\log_3x)^2=3\log_3x^+4\\\\Let u=\log_3x\\\\u^2-3u-4=0\\(u-4)(u+1)=0\\u=4 \\4=\log_3x\\x=3^4=81\\\\u=-1\\-1=\log_3x\\x=3^{-1}=1/3\)
The average high temperature during the hottest month in Beijing, China, is 72°F. The average high temperature during the coldest month in Beijing is 18°F. The function 1 =27 cos( π/6(m-6)) +45, where m represents the number of months after January, models the temperature throughout the year in Beijing. During which monke in the year would the temperature reach 55°F?
- August
- September
- November
- December
(it'll be SEPTEMBER, i just couldn't find the answer for it anywhere else, so here ya gooo.)
Answers
Answer:
- September
Step-by-step explanation:
The temperature in Beijing, in m months after January, is given by the following equation:
\(T(m) = 27\cos{((\frac{\pi}{6})(m-6))} + 45\)
In which m is the number of months after January.
During which month in the year would the temperature reach 55°F?
We have to find m for which: T(m) = 55. So
\(T(m) = 27\cos{((\frac{\pi}{6})(m-6))} + 45\)
\(55 = 27\cos{((\frac{\pi}{6})(m-6))} + 45\)
\(27\cos{((\frac{\pi}{6})(m-6))} = 10\)
\(\cos{((\frac{\pi}{6})(m-6))} = \frac{10}{27}\)
Now, we apply the inverse cosine, on both sides of the equation, to find the value of m.
\(\cos^{-1}{\cos{(\frac{\pi}{6})(m-6)}} = \cos^{-1}{\frac{10}{27}}\)
Now, with the help of a calculator, in radians:
\(\frac{\pi}{6}(m-6) = 1.19\)
\(\pi m - 6\pi = 6*1.19\)
\(\pi m = 6*1.19 + 6 \pi\)
\(m = \frac{6*1.19 + 6 \pi}{\pi}\)
\(m = 8.27\)
8.27 months after January, since 8.27 + 1 = 9.28, it happens during the month of September.
Answer: September
Step-by-step explanation:
Edge
determine whether y=2x^2 +1 is a function
Answers
Answer: Yes, this is a function!
Step-by-step explanation: Here are the requirements for determining if a 2-variable equation is a function or not.
2.
Each input should correspond to only one output
. In our case, any value of x you put into this equation only gives one value of y. We can verify this graphically using a simple test called the
vertical line test.
To do this, graph the function with the x axis being the horizontal axis and the y axis being the vertical axis (this matters!) In our case, this will be a parabola opening upwards. The test says that if I can draw vertical lines through every part of the graph and each vertical line only crosses the graph once, the equation is a function. In our case, I can draw vertical lines through everywhere in a parabola and they will only cross once. This shows that we have a function!
Hope this helps!
Bye for now,
Iz
What is the greatest common factor of 8,16,40
Answers
Step-by-step explanation:
To find the greatest common factor (GCF) of 8, 16, and 40, we can determine the largest number that evenly divides all three of them.
Let's first find the prime factorization of each number:
- 8 = 2 * 2 * 2
- 16 = 2 * 2 * 2 * 2
- 40 = 2 * 2 * 2 * 5
Now, let's identify the common factors by finding the minimum exponent for each prime factor:
- 2 is a common factor with an exponent of 2 (appearing twice in the prime factorization of 8 and 16).
- 5 is not a common factor since it appears only in the prime factorization of 40.
The GCF is obtained by multiplying the common factors with their respective minimum exponents:
GCF = 2^2 = 4
Therefore, the greatest common factor of 8, 16, and 40 is 4.