What is the value of x in the equation -6x = 5x + 22?
Options:
A. ) –22
B. ) –2
C. ) 2
D. )22
Thank you!
Answers
Answer:
D
Step-by-step explanation:
collect like terms and divide by -11
Related Questions
hellp with this i dont understand please

Answers
| t | 0 | 1 | 2 | 3 | 4 | 5 |
| d | 0 | 60 | 120 | 180 | 240 | 300|
\(\rule{300pt}{3pt}\)
#bGraph is attached!!~\(\rule{300pt}{3pt}\)
#cTake any two points from the table and find the slope.
Points:
(1,60) & (3,180)
\( \large \tt \: m = \frac{ y_{2} - y_{1}}{ x_{2} - x_{1}} \)
\( \sf \: m = \frac{180 - 60}{3 - 1} \)
\( \sf \: m = \frac{120}{2} \)
\( \sf \: m = \cancel \frac{120}{2} = 60\)
Therefore, Slope is 60..

Find the equation of the line containing the point
P(−2, 3)
and perpendicular to the graph of
3x + 9y = −2.

Answers
Answer:
Step-by-step explanation:
y = 3x + 9
Wayward shoes spends $13 making each pair of its slip-on sneakers. Last week, they sold 95 pairs of these sneakers for $45 each. How much profit did Wayward shoes make last week.
Answers
Answer:
$3040 profit made
Step-by-step explanation:
$13×95=$1235 cost to make all the shoes they sold
$45×95=$4275 money she made
$4275-$1235=$3040 profit
Show the algorithm/abstract strategy to justify the 3/5?
Answers
The algorithm/abstract strategy to justify the fraction 3/5 involves interpreting it as a division, performing the division, and obtaining the decimal representation as the results.
To justify the fraction 3/5, we can use the concept of division and understand it as a ratio or proportion.
Algorithm/Abstract Strategy:
Start with the numerator, which is 3.
Identify the denominator, which is 5.
Interpret the fraction as a ratio or comparison between the numerator and denominator.
Understand that 3/5 represents a division where the numerator (3) is divided by the denominator (5).
Perform the division: 3 ÷ 5.
Simplify the division to its simplest form, if necessary.
The result of the division, in this case, is the decimal representation of the fraction.
If required, convert the decimal representation to a percentage or any other desired form.
For example, if we perform the division 3 ÷ 5, the result is 0.6.
So, 3/5 can be justified as the ratio or proportion where the numerator (3) is divided by the denominator (5) resulting in 0.6.
For similar question on algorithm/abstract strategy.
https://brainly.com/question/31332020
#SPJ8
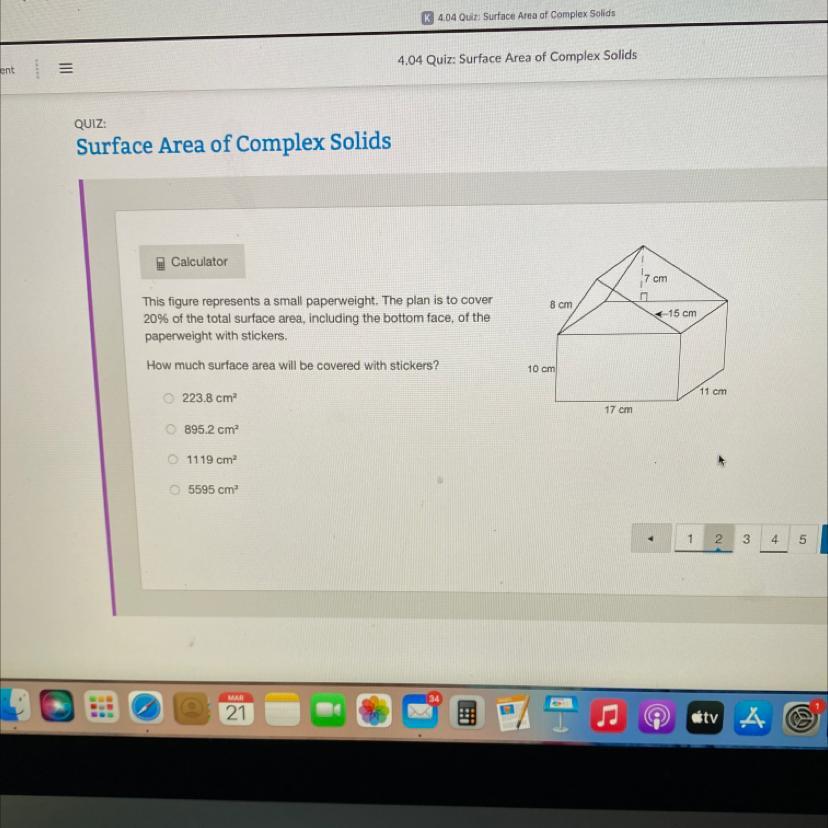
Calculator
cm
n
8 cm
This figure represents a small paperweight. The plan is to cover
20% of the total surface area, including the bottom face, of the
paperweight with stickers.
15 cm
How much surface area will be covered with stickers?
10 cm
223.8 cm
11 cm
17 cm
895.2 cm?
1119 cm
5595 cm
1
2
3
4
5
Answers
Answer:
223.8
Step-by-step explanation:
I failed the test to get the answer
Answer:
the answer is 223.8
Step-by-step explanation:
When x > 0 and y > 0, what expression is equivalent to √180x^9y^16 in simplest form?
Answers
Answer:
\(6x^4y^8\sqrt{5x}\)
Step-by-step explanation:
\(\textsf{When $x > 0$ and $y > 0$, we want to find the expression that is equivalent to}\) \(\sqrt{180x^9y^{16}}.\)
\(\textsf{First, apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(\sqrt{180}\sqrt{x^9}\sqrt{y^{16}}\)
\(\textsf{Rewrite $x^9$ as $x^{8+1}$:}\)
\(\sqrt{180}\sqrt{x^{(8+1)}}\sqrt{y^{16}}\)
\(\textsf{Apply the exponent rule:} \quad a^{b+c}=a^b \cdot a^c\)
\(\sqrt{180}\sqrt{x^{8}\cdot x^1}\sqrt{y^{16}}\)
\(\sqrt{180}\sqrt{x^{8}}\sqrt{x}\sqrt{y^{16}}\)
\(\textsf{Apply\:the\:radical\:rule:\:}\sqrt[n]{a^m}=a^{\frac{m}{n}},\:\quad a\geq 0\)
\(\sqrt{180}\;x^{\frac{8}{2}}\sqrt{x}\;y^{\frac{16}{2}}\)
\(\sqrt{180}\;x^4\sqrt{x}\;y^8\)
\(\sqrt{180}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Rewrite $180$ as $(6^2 \cdot 5)$:}\)
\(\sqrt{6^2 \cdot 5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{ab}=\sqrt{a}\sqrt{b}\)
\(\sqrt{6^2} \sqrt{5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{a^2}=a, \quad a \geq 0\)
\(6 \sqrt{5}\sqrt{x}\;x^4\;y^8\)
\(\textsf{Apply the radical rule:} \quad \sqrt{a}\sqrt{b}=\sqrt{ab}\)
\(6 \sqrt{5x}\;x^4\;y^8\)
\(\textsf{Rearrange:}\)
\(6x^4y^8\sqrt{5x}\)
\(\textsf{Therefore, when $x > 0$ and $y > 0$, the expression that is equivalent to}\)
\(\sqrt{180x^9y^{16}}\;\textsf{is}\;\;\boxed{6x^4y^8\sqrt{5x}}\:.\)
Lucas is planting grass on the shaded portions of the yard. What will be the total area covered by grass?
Answers
Complete Question:
Lucas is planting grass on the shaded portions of the yard. What will be the total area of covered by grass? Fill in the missing.
Part A= 12 x ? = ? ft²
Part B= 0.5 x ? x 9 = ?ft²
Part C= 0.5 x 7 x ? = ?ft²
Total Area= ?ft²
Answer:
\(A = 108ft^2\)
\(B = 27ft^2\)
\(C = 24.5ft^2\)
\(Area = 159.50ft^2\)
Step-by-step explanation:
Given
See attachment
From the attachment;
Part A is a rectangle with dimension 9ft by 12ft
So,
\(A = 12ft * 9ft\)
\(A = 108ft^2\)
Part B is a triangle with dimension: height = 6 and base = 9
The height is calculated as:
\(Height = 12ft - 6ft = 6ft\)
And the base is:
\(Base = 18ft - 9ft = 9ft\)
So, the area is:
\(B = 0.5 * 6ft * 9ft\)
\(B = 27ft^2\)
Part C is a triangle with dimension: height = 7 and base = 7
So, the area is:
\(C = 0.5 * 7 * 7ft^2\)
\(C = 24.5ft^2\)
Total Area is:
\(Area = A + B + C\)
\(Area = 108ft^2 + 27ft^2 + 24.5ft^2\)
\(Area = 159.50ft^2\)

In an orchard 2/5 of the trees are banana trees, 1/4 of the trees are orange trees and the rest are apple trees. If there are 220 trees in all, find the number of each kind
Answers
Answer: banana- 88
Orange-55
Apple-143
Step-by-step explanation:
220 divided by 5, times 2,
that’s the banana trees
220 divided by 4, that’s the oranges
Add the answers together
Take the answer away from 220 that’s the apples
Graph each function between 0 and 2

Answers
The function oscillates between two horizontal asymptotes, y=3 and y=-3, as x approaches the vertical asymptotes.
How to study graph?
To graph the function y=3cot(x) between 0 and 2, we can start by identifying the key characteristics of the cotangent function. The cotangent function is defined as the ratio of the adjacent side to the opposite side of a right triangle, with respect to a given angle. As such, the cotangent function is periodic with a period of π and has vertical asymptotes at x=nπ, where n is an integer.
The coefficient of 3 in the given function y=3cot(x) vertically stretches the function by a factor of 3, and does not affect the period or the vertical asymptotes.
Between 0 and 2, there are two vertical asymptotes at x=0 and x=π. To graph the function, we can plot a few points along the curve, using the symmetry properties of the cotangent function. Specifically, the cotangent function is odd, meaning that cot(-x)=-cot(x), and thus the graph is symmetric about the origin.
At x=π/4, we have cot(π/4)=1, and thus y=3cot(π/4)=3. Similarly, at x=3π/4, we have cot(3π/4)=-1, and thus y=3cot(3π/4)=-3. Using the symmetry property, we can also plot points at x=-π/4 and x=-3π/4, with y=3cot(-π/4)=-3 and y=3cot(-3π/4)=3, respectively.
Connecting these points with smooth curves, we can see that the graph of y=3cot(x) oscillates between two horizontal asymptotes, y=3 and y=-3, as x approaches the vertical asymptotes at x=0 and x=π.
Overall, the graph of y=3cot(x) between 0 and 2 can be summarized as follows:
There are two vertical asymptotes at x=0 and x=π.
The function oscillates between two horizontal asymptotes, y=3 and y=-3, as x approaches the vertical asymptotes.
The graph is symmetric about the origin.
To know more about functions visit :-
https://brainly.com/question/11624077
#SPJ1

Two pedestrians simultaneously left two villages 27 km apart and walked toward each other, meeting after 3 hours. The first pedestrian walked at a speed of 4 km per hour. At what speed (in km per h) did the second pedestrian walk?
Answers
The speed of the second pedestrian is 5 kilometers per hour.
At what speed did the second pedestrian walk?Let's say that the speed of the second pedestrian is S.
We know that the other pedestrian walks at a speed of 4km/h, and they (together) travel a distance of 27km in 3 hours, then we can write the linear equation:
(4km/h + S)*3h = 27km
It says that both pedestrians work, together, a total of 27km in 3 hours.
Now we can solve that linear equation for S, to do this, we need to isolate S in the left side of the equation.
4km/h + S = 27km/3h = 9 km/h
S = 9km/h - 4km/h = 5km/h
The speed of the second pedestrian is 5 kilometers per hour.
If you want to learn more about speed:
https://brainly.com/question/4931057
#SPJ1
Use the recursive formula f(n) = 0.4 ⋅ f(n − 1) + 12 to determine the 2nd term if f(1) = 4.
Answers
Answer:
f(2) = 13.6
Step-by-step explanation:
Using the recursive formula and f(1) = 4 , then
f(2) = 0.4 f(1) + 12 = (0.4) × 4) + 12 = 1.6 + 12 = 13.6
consider the expresson 1/2x to the second power +x+7. complete 2 descriptions of the part of the expression
Answers
The entire expression is a sum with 0 factors
The coefficients are 1/2, 1 and 7
How to describe the expressionFrom the question, we have the following parameters that can be used in our computation:
1/2x² + x + 7
The above expression is a quadratic expression and it has three terms
Quadratic expressions with real roots have 2 factors, otherwise it would have 0 factor
The expression 1/2x² + x + 7 does not have a real root because
b² < 2ac
Also in the expression, the coefficients are 1/2, 1 and 7
i.e. a = 1/2, b = 1 and c = 7
Read more about quadratic expression at
https://brainly.com/question/1214333
#SPJ1
Complete question
consider the expresson 1/2x² + x + 7.
complete 2 descriptions of the part of the expression
The entire expression is a sum with __ factors
The coefficients are _
to determine whether families with children would use school vouchers to send their children to charter schools, from which of the following populations should you select a sample?
Answers
Parents of children under the age of 18.
It is seldom feasible to get data from every member of a group of individuals when conducting research on them. In its place, you pick a sample. The population that will actually take part in the study is the sample. It is referred to as a sampling method. You can use one of the following two main sampling techniques in your study:
Random selection is a key component of probability sampling, which enables you to draw robust statistical conclusions about the entire group.
Non-probability sampling entails non-random selection based on practicality or other factors, making it simple to gather data.
To know more about sampling visit: brainly.com/question/13287171
#SPJ4
Please help with this

Answers
Answer:
C) 42
Step-by-step explanation:
The parallel lines divide the transversals proportionally.
x/35 = 30/25
x = 35(6/5) . . . . multiply by 35, reduce the fraction
x = 42
A city council consists of six Democrats and seven republicans. If a committee of four people is selected, find the probability of selecting two Democrats and two Republicans.
Answers
Answer:
\(\bold{\dfrac{63}{143}}\)
Step-by-step explanation:
Number of Democrats = 6
Number of Republicans = 7
Total number of members = 6+7 = 13
To find:
Probability of selecting two Democrats and two Republicans if 4 members are selected in the committee = ?
Solution:
This is a selection problem.
Total number of ways to select 4 members in the committee out of total 13 = \(_{13}C_4 = \dfrac{13\times 12\times 11\times 10}{4\times 3\times 2} = 715\)
Number of ways to select 2 Democrats = \(_{6}C_2 = \dfrac{6\times 5}{2} = 15\)
Number of ways to select 2 Republicans = \(_{7}C_2 = \dfrac{7\times 6}{2} = 21\)
Number of ways to select 2 Democrats and 2 Republicans = 15 \(\times\) 21 = 315
Formula for probability of an event E can be observed as:
\(P(E) = \dfrac{\text{Number of favorable cases}}{\text {Total number of cases}}\)
Here, required probability:
\(\dfrac{315}{715} = \bold{\dfrac{63}{143}}\)
which value of y makes the inequality 3y^2+2(y-5)>8 true?
A. y = 0
B. y = –1
C. y = –2
D. y = –3
Answers
you substitute each of the values into y
3(-3)^2+2(-3-5)>8
you square the -3 and then multiply by 3, you’re left with 27+2(-3-5)>8
You then subtract -3-5 inside the parentheses and are left with 27+2(-8)>8 multiply the 2 and -8
27+(-16)>8 or 27-16>8
Subtract and you’re left with 11>8
All the others are the same steps, but they are not true
The student government snack shop sold 32 items this week.
For each snack type, what percentage of all snacks sold were of that type? Do not round your answers.

Answers
The percentages of each snack type that were sold are given as follows:
Fruit cup: 25%.Veggie sticks: 18.75%.Chips: 43.75%.Water: 12.5%.How to obtain the percentage?A percentage is one example of a proportion, as it is obtained by the number of desired outcomes divided by the number of total outcomes, and then multiplied by 100%.
Hence the percentages for each type are obtained as follows:
Fruit cup: 8/32 x 100% = 25%.Veggie sticks: 6/32 = 18.75%.Chips: 14/32 = 43.75%.Water: 4/32 = 12.5%.More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
Polynomial multiple choice help

Answers
2. A graph
4. C- Neither even or odd
5. A- 32
—
3. A or D (not sure)
1. A,B or C but not D (I don’t think)
Hope this helps :)
Determine the value of a if f(x) =(ax²-1 if x < 1 a(x² - 2x + 1) ifx>1 is continuous atx = 1.
Answers
-1 does not equal 0, the equation is not true for any value of "a". This means that there is no value of "a" for which the function f(x) is continuous at x = 1.
To determine the value of "a" for which the function f(x) is continuous at x = 1, we need to check if the left-hand limit and the right-hand limit of f(x) as x approaches 1 are equal, and if the value of f(x) at x = 1 is equal to these limits.
First, let's calculate the left-hand limit of f(x) as x approaches 1. For x < 1, the function is given by f(x) = (ax² - 1). To find the left-hand limit, we substitute x = 1 into this expression:
lim(x→1-) f(x) = lim(x→1-) (ax² - 1) = a(1²) - 1 = a - 1.
Next, let's calculate the right-hand limit of f(x) as x approaches 1. For x > 1, the function is given by f(x) = (a(x² - 2x + 1)). Substituting x = 1 into this expression, we have:
lim(x→1+) f(x) = lim(x→1+) (a(x² - 2x + 1)) = a(1² - 2(1) + 1) = a(1 - 2 + 1) = a.
For the function f(x) to be continuous at x = 1, the left-hand limit and the right-hand limit should be equal. Therefore, we have:
a - 1 = a.
To solve this equation for "a," we subtract "a" from both sides:
-1 = 0.
Since -1 does not equal 0, the equation is not true for any value of "a". This means that there is no value of "a" for which the function f(x) is continuous at x = 1.
for such more question on equation
https://brainly.com/question/17482667
#SPJ8
The volume of this sphere is 15500cm3.
Work out the length of the radius,
r
.
Give your answer rounded to 1 DP
Answers
Answer:
r = 15.5
Step-by-step explanation:
4/3 pi r^3 = 15500 cm^3
r^3 = 15500 ÷ (4/3 pi)
r^3 = 3700.35
r = cube root of 3700.35
r = 15.467
r = 15.5
Answer:
4/3 π r³= 15500
r³=15500×3/4×7/22
r≈15.2 cm
Step-by-step explanation:
Write an equation of the line in slope-intercept form.

Answers
Answer:
Step-by-step explanation:
Y-intercept is -2.
Using slope formula, 2-(-2)/2-0 = 4/2 = 2 = slope.
Plugging into slope-intercept form:
y=mx+b => y=2x-2
what polynomial should be subtracted from 3x^2+4x-1 to get the difference equal to 0
Answers
Answer:
\( {x}^{2} + \frac{4}{3} x - \frac{1}{3} \)
can be subtracted
What is the symbol ~, if you're trying to find the probability of ~A?
the addition probability
the probability of the event not happening
the multiplication probability
None of these choices are correct.
Answers
The symbol ~ (tilde) is commonly used to represent the negation or complement of an event. When we refer to ~A, it means "not A" or "the complement of A." In terms of probability, ~A represents the event not happening or the event A occurring.
an investment that you bought ____ and sold for ___ made a profit
A.400, 500
B.500,300
C.500, 400
D.400, 300
Answers
The question mentions you make a profit, which is to make more money than what you spent or put in. All other choices would make the statement say you ended up having less money, which is money lost, not profit.
A tank is full of water. Find the work (in ft-lb) required to pump the water out of the spout. Use the fact that water weighs 62.5 lb/ft3. (Round your answer to the nearest whole number.) 3 ft6 ft12 ft A frustum of a cone with a spout is given. The smaller radius is 3 ft, the larger radius is 6 ft, and the height is 12 ft.
Answers
The work required to pump the water out of the spout is approximately 64,307,077 ft-lb
To find the work required to pump the water out of the spout, we need to calculate the weight of the water in the tank and then convert it to work using the formula: work = force × distance.
First, let's calculate the volume of water in the tank. The frustum of a cone can be represented by the formula: V = (1/3)πh(r1² + r2² + r1r2), where r1 and r2 are the radii of the two bases and h is the height.
Given r1 = 3 ft, r2 = 6 ft, and h = 12 ft, we can calculate the volume:
V = (1/3)π(12)(9 + 36 + 18) = 270π ft³
Now, we can calculate the weight of the water using the density of water:
Weight = density × volume = 62.5 lb/ft³ × 270π ft³ ≈ 53125π lb
Next, we convert the weight to force by multiplying it by the acceleration due to gravity (32.2 ft/s²):
Force = Weight × acceleration due to gravity = 53125π lb × 32.2 ft/s² ≈ 1709125π lb·ft/s²
Finally, we can calculate the work by multiplying the force by the distance. Since the water is being pumped out of the spout, the distance is equal to the height of the frustum, which is 12 ft:
Work = Force × distance = 1709125π lb·ft/s² × 12 ft ≈ 20509500π lb·ft ≈ 64307077 lb·ft
for more search question water
https://brainly.com/question/17120212
#SPJ8
A town of 3200, grows at a rate of 25% every year. Find the size of the city in 10 years.
Answers
The size of the city in 10 years is equal to 29,802.32
Given the following data:
Population = 3200Growth rate = 25% = 0.25Time = 10 years.To calculate the size of the city in 10 years:
In this exercise, you're required to determine the size of this city in the next ten (10) years.
The formula for exponential growth.Mathematically, the exponential growth of a population is given by this formula;
\(P = a(1+r)^t\)
Where:
P is the total population.r is the growth rate.t is the time.Substituting the given parameters into the formula, we have;
\(P = 3200(1+0.25)^{10}\\\\P = 3200(1.25)^{10}\\\\P = 3200 \times 9.3132\)
P = 29,802.32
Read more on here: https://brainly.com/question/23213182
Determine whether the data come from a normally distributed population. Choose the correct answer below. A. The distribution is not normal. The points are not reasonably close to a straight line. B. The distribution is normal. The points show a systematic pattern that is not a straight-line pattern. C. The distribution is not normal. The points show a systematic pattern that is not a straight-line pattern. D. The distribution is normal.
Answers
The distribution is not normal. The points show a systematic pattern that is not a straight-line pattern curved over mean.
A normal distribution is a type of data distribution in which the data points form a symmetric, bell-shaped curve around the mean.
The data points in the example provided show a systematic pattern that is not a straight-line pattern, indicating that the data does not come from a normally distributed population.
This is because the points are not reasonably close to a straight line, which is a characteristic of a normal distribution.
Learn more about mean here
https://brainly.com/question/15323584
#SPJ4
what is the reciprocal of 2 8/9
Answers
9/26
2 8/9 = 26/9
Reciprocal of 16/9 is 9/26
Find the total area of the shaded region. Ay 1.5- 14 x=5y3 (5,1) * = 5y? 0.5- х 07 0 2.5 5 7.5 Find the area of the region enclosed by the curves x= x = 7y?, x=0, and y=1. The area of the region enclosed by the curves is (Type a simplified fraction.)
Answers
The total area of the shaded region for the region x = 5y³ , x = 5y² in the interval ( 5, 1 ) is equal to ( 5 / 12 ).
From the attached graph :
The area of the shaded region :
x = 5y³ , x = 5y² for the interval ( 5, 1 ) is equal to :
= \(\int\limits^1_0 {( 5y^{2 } - 5y^{3 }}) \, dy\)
= [ ( 5y³/3 ) - ( 5y⁴ / 4 ) ]\(| \limits^1_0\)
Substitute the lower limit and upper limit we get,
= (5 /3 )( 1 )³ - 0 - ( 5 / 4 )( 1⁴) + 0
= ( 5 / 3 ) - ( 5 / 4 )
= ( 20 - 15 ) / 12
= 5 / 12
Therefore, the total area of the shaded region in the given graph for the lower and upper limit is equal to ( 5 / 12 ) .
The given question is incomplete, I answer the question in general according to my knowledge:
Find the total area of the shaded region x = 5y³ , x = 5y² for the interval
( 5, 1 ).
Graph is attached.
learn more about area here
brainly.com/question/27683633
#SPJ4

Pls hellllp will gib brainliest

Answers
Answer:
B
Step-by-step explanation:
312-96=216
216/24=9
Answer:
B
Step-by-step explanation:
24x9+96