What is the value of x if 15 = 5x +45?
Answers
Answer:
x=-6
Step-by-step explanation:
start by subtracting 45 on both sides to get the variable by itself.
Next divide by 5 to get the value of x.
Use a Calculator to help :)
Related Questions
What is (gof)(x) if f(x) = 3x - 1 and g(x) = 4x² + 9?
Answers
Step-by-step explanation:
(gof)(x) is basically g(f(x))
= 4 × (3x - 1)² + 9
= 4 × (9x² - 6x + 1) + 9
= 36x² - 24x + 4 + 9
= 36x² - 24x + 13
Flora drew the following graph to answer the question. What was her mistake when she drew her graph? (NO LINKS)

Answers
Answer:
Her elevation went down too quickly, if she is going down 300 ft per hour at a constant rate, at 1 hour, she should be at 2700 feet. It should take her about 10 hours to get down the mountain.
this is due in 30 mins

Answers
11) The pre-image, R at the point (-2, 3) on the grid shown produces an image following the reflection across the line y = 2·x - 3 as follows;
I. The line \(\overline{RR'}\) which is obtained from the image R' following a reflection across the line y = 2·x - 3, is perpendicular to the line y = 2·x - 3, because the points R and R' are vertically opposite each other, therefore, the slope is the negative inverse of the slope of y = 2·x - 3, which is -0.5
II. Please find attached the graph made using MS Excel showing the points R and R'
What is a reflection transformation?A reflection transformation is one in which a point is reflected across a line such that the distances of the image and the pre-image from the line are the same and the line acts like a mirror producing an image of the object.
The coordinates of point R = (-2, 3)
The equation of the line of reflection is; y = 2·x - 3
The coordinates of the image of a point, (x₁, y₁) reflected across a line, a·x + b·y + c = 0, is found as follows;
The image of is found using the formula;
\(\dfrac{x - x_1}{a} =\dfrac{y-y_1}{b} = -\dfrac{2\cdot (a\cdot x_1+b\cdot y_1+c)}{a^2+b^2}\)
The equation, y = 2·x - 3, can be expressed in the form a·x + b·y + c = 0, as follows;
y = 2·x - 3
0 = 2·x - 3 - y
Therefore;
a = 2, b = -1, and c = -3
(x₁, y₁) = (-2, 3)
\(\dfrac{x - (-2)}{2} = -\dfrac{2\times (2\times (-2)- 3-3)}{2^2+(-1)^2}=4\)
\(\dfrac{x +2}{2} = 4\)
x = 2× 4 - 2 = 6
x = 6
\(\dfrac{y-3}{-1} = 4\)
y = 4 ×(-1) + 3 = -1
The coordinates of the image, (x, y) = (6, -1)
The slope of the line is -(1/2)
The equation of the perpendicular line is therefore;
(y - 3) = -0.5·(x - (-2)) = -0.5·x - 1
y = -0.5·x - 1 + 3 = -0.5·x + 2
Equation of the perpendicular line through R; y = -0.5·x + 2
The intersection point is therefore;
-0.5·x + 2 = 2·x - 3
2.5·x = 5
x = 5 ÷ 2.5 = 2
y = 2×2 - 3 = 1
y = 1
The point is therefore, (2, 1)
The difference in the x-values = 2 - 2 = 4
The difference in the y-value = 1 - 3 = -2
Therefore, 4 is added to the x-value of the point (2, 1) and 2 is subtracted to get the image as follows;
(x, y) = (2 + 4, 1 - 2) = (6, -1)
The slope of \(\overline{RR'}\) = (3 - (-1))/(-2 - 6) = -0.5
b. Graphically, the equation of the line \(\overline{RR'}\) can be used to find the point R', by adding the horizontal distance and subtracting the vertical distance of the point R from the the point of intersection of the two lines.
Please find attached the graph showing R and the image R' created with MS Excel.
Learn more about reflection transformation in geometry here;
https://brainly.com/question/4070544
#SPJ1
Which function represents a reflection of f(x) = 2*

Answers
Answer:
h(x)=2x-1
Step-by-step explanation:
The Given function is
f(x) =2*(0.35)* x
→y=0.7* x→Pre image
The line passes through first and third quadrant.
it is equation of straight line passing through origin and slope =0.7.
When this line is reflected over y axis , the equation of new line will be
→y= - 0.7 x⇒image
Slope of image will be = -0.7
The Image passes through Second and fourth Quadrant.
John has $50 and his sister has $100. John is saving $6 per week and his sister is saving $4 per week. Which of the following equations will lead you to find when John and his sister will have the same amount of money?
6x - 50 = 4x - 100
6x + 50 = 4x + 100
6x/50 = 4x/100
10x + 150 = 0
Answers
The correct expression is 6x + 50 = 4x + 100
What is expression?A sentence with variable and numbers connected by one or more operations is called an expression.
Given that, John has $50 and his sister has $100. John is saving $6 per week and his sister is saving $4 per week.
Amount John have = 6x+50
Amount his sister have = 4x+100
Therefore, establishing the equation, the equations will be equal, since the amount both have is equal, therefore, for equating the expression will find the value x which is the number of week.
6x + 50 = 4x + 100
6x-4x = 100-50
2x = 50
x = 50/2
x = 25
Therefore, they will have equal amounts in 25 weeks.
Hence, the equation for them having the same amount is 6x + 50 = 4x + 100.
For more references on expressions, click;
https://brainly.com/question/14083225
#SPJ1
Identify the error below. Then, solve the equation correctly.

Answers
Answer:
Error: +3x should be -3x
x should equal 3
Step-by-step explanation:
In this problem, you have to pay attention how values are transferred from one side to the other. This includes paying attention t the signs.
In 3x + 4 = 8x - 11, you want to try an keep all the values positive
3x + 4 = 8x - 11
- 3x - 3x
4 = 5x - 11
+11 +11 <--This part of the equation was correct.
15 = 5x
/5 /5 <--This part of the equation should result in dividing by 5
3 = x
Hope this helps!
How many cubes with an edge length of 1/5 inch are needed to build a cube with an edge length of 1 inches?
Answers
125 cubes with an edge length of 1/5 inch are needed to build a cube with an edge length of 1 inch.
What is a cube?A cube is a 3-dimensional solid shape with six square faces that are all congruent, and with all edges of equal length.
The volume of a cube is calculated by cubing the length of one of its edges.
To find the number of cubes with an edge length of 1/5 inch that are needed to build a cube with an edge length of 1 inch, we need to calculate the ratio of the volumes of the two cubes.
The volume of the larger cube with an edge length of 1 inch is:
V_large = (1 inch)^3 = 1 cubic inch
The volume of the smaller cube with an edge length of 1/5 inch is:
V_small = (1/5 inch)^3 = 1/125 cubic inches
To find the number of small cubes, we need to divide the volume of the larger cube by the volume of the smaller cube:
Number of small cubes = V_large / V_small = 1 cubic inch / (1/125 cubic inches) = 125
To know more about volume visit:
https://brainly.com/question/4678941
#SPJ1
The square root of 75 is_____ (round to the hundredths place if necessary)
Answers
Hope this helps =)
A prism has base of length 15cm and width x cm The cross section is right angled triangle The height is 4cm less than its width The volume is 440cm3
Show that
3xsq -12x -176

Answers
Answer:
665tggy66yh345666ygvv
The perimeter of a rectangular lawn i 50 meter. It' 16 meter long how wide i it?
Answers
The width of the rectangle is 9 meter.
Now, According to the question:
The perimeter of a rectangle is defined as the sum of all the sides of a rectangle. For any polygon, the perimeter formulas are the total distance around its sides. In case of a rectangle, the opposite sides of a rectangle are equal and so, the perimeter will be twice the width of the rectangle plus twice the length of the rectangle and it is denoted by the alphabet “p”.
Now, Solving the problem:
Perimeter of rectangle is 50 meter sq.
Length of the rectangle(L) is 16 meter.
We have to find the width (W) of the rectangle.
We know that,
Perimeter of rectangle is = 2 (L + W)
50 = 2(16 + W)
50 = 32 + 2W
2W = 50 - 32
2W = 18
W = 18/2
W = 9
Hence, The width of the rectangle is 9 meter.
Learn more about Perimeter of rectangle at:
https://brainly.com/question/22109593
#SPJ4
Pleaseeeee helppp domain and range

Answers
Answer:
\(-5\leq x\leq 3\)
Step-by-step explanation:
The reason is that if you count each line on the graph you see that it starts at -5 and ends at 3.
(Hint: each line on the graph is incrementing by 1)
Hope this helps! :)
Please mark as brainiest if this worked or ask me a question if you do not understand :)
Given that a = 6i- 3j, find:
a the unit vector in the same direction of a
b the angle that a makes with the positive x-axis.
Answers
The unit vector in the same direction will be equal to (6 i/5.1 - 3 j/5.1).
What is a Vector?A vector is a quantity with both magnitude and direction in physics. It is often depicted by an arrow with the same direction as the amount and a length proportionate to the size of the quantity.
A vector lacks position, but has magnitude and direction. A vector is therefore unaffected by displacement parallel to itself as far as its length is unaltered.
As per the given data in the question,
The unit vector is calculated as:
\(\vec u_a=\frac{\vec a}{||\vec a||}\)
\(\vec a= x \vec i+y \vec j\)
Now, calculate the magnitude of the vector,
\(\vec a\) = √(x² + y²)
\(|\vec a|\) = √6² - 3²
= √36 - 9
= 5.1
So, the unit vector will be,
\(\vec u_a\) = (6 i - 3 j)/5.1
To know more about vector:
https://brainly.com/question/29740341
#SPJ1
Point C is located at (1, 2), and point D is located at (-4,-2). Find the point that is the distance from point C
to point D. (1 point)
a. (-0.25, 1)
b. (-1.5,0)
c. (-0.5, 1.5)
d. (0.25, 2.25)
Answers
Answer:
The answer would be c
Step-by-step explanation:
i choosed c because u have da negative sign in front of 4 and 2 and positive numbers with 1 and 2
Answer:
b
Step-by-step explanation:
I think this means to find the mid-point(?) of the line which by doing that you take both x-values and you add them and then divide by two, and then you take both y-values and add them and then divide by two. So you have: (1+-4)=-3, (-3/2)=-1.5
-1.5=x
(2+-2)=0, (0/2)=0
0=y
(-1.5, 0)
simplify 3 to the 2nd power + 1 x 2
Answers
Answer: The answer is 20
Step-by-step explanation:
\(\huge\text{Hey there!}\)
\(Equation:\)
\(\rm{3^2 + 1\times 2}\)
\(Simplifying:\)
\(\rm{3^2 + 1\times 2}\)
\(\rm{= 3\times 3+ 1\times 2}\)
\(\rm{= 9 + 1\times2}\)
\(\rm{= 9 + 2}\)
\(\rm{= 11}\)
\(Therefore, your\ answer\ should\ be:\)
\(\huge\boxed{\frak{11}}\huge\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Which of the following correctly graphs the system of equations?
{y=x−3
y=−2x+3




Answers
The third one
This graph is the only one that shows the correct slops with the correct y intercepts (-3 and 3)
help help help help help help

Answers
use desmos it help lot


A local charity holds a carnival to raise money. In one activity, participants make a $3 donation for a chance to spin a wheel that has 10 spaces marked with the values 0, 1, 2, 5, and 10. The participant wins the dollar amount marked on the space on which the wheel stops. Let X represent the value of a spin. The distribution of X is given in the table.
A 2-column table with 5 rows. Column 1 is labeled value of a spin with entries 0, 1, 2, 5, 10. Column 2 is labeled probability with entries 0.4, 0.2, 0.2, 0.1, 0.1.
What is the median of the distribution?
1
1.5
2
2.1
Answers
Answer:2
Step-by-step explanation:
The median of the probability distribution given in the table is 1.
Given that X, the value of a spin and the corresponding probability distribution.
X : 0 1 2 5 10
P(X) : 0.4 0.2 0.2 0.1 0.1
CF : 0.4 0.6 0.8 0.9 1
So the sum of the cumulative frequency = 1
We have to find the value where the half of the cumulative frequency lies in.
1/2 = 0.5
0.5 lies in between 0.4 and 0.6.
The value of the spin that corresponds to 0.6 is 1.
So the median of the distribution is 1.
Learn more about Median of the Distribution here :
https://brainly.com/question/11146087
#SPJ7
which veal represents the functions ?
A. graph A only
B. graph D only
C. graph B and graph D
D. graph C and graph D

Answers
hola quien habla español bueno ya no Adios :)
Answer:
C.(B and D
Step-by-step explanation:
Suppose a golf club company has designed a new club, which it claims will allow a professional golfer to make a hole in 120% of the time and an amateur golfer 10% of the time. Professional an amateur golfers sign up to play 5 games of 18 holes each
Answers
A professional golfer to make about 40.7 holes over 5 rounds of golf with the new club, while an amateur golfer would only make about 1.6.
First, let's define some variables to represent the probabilities of making a hole for a professional golfer and an amateur golfer:
Let p be the probability that a professional golfer makes a hole with the new club.
Let q be the probability that an amateur golfer makes a hole with the new club.
According to the company's claims, we know that:
p = 1.2q (since the professional golfer makes a hole 120% of the time, which is 1.2 times the probability of the amateur golfer making a hole)
Next, we need to determine the probability of each golfer making a hole during one round of golf, which consists of 18 holes. Let's assume that each hole is independent of the others, meaning that the outcome of one hole does not affect the outcome of another. In that case, the probability of making at least one hole in a round can be calculated using the complement rule:
The probability that a professional golfer makes at least one hole in a round is 1 minus the probability that the golfer misses every hole: \(1 - (1-p)^{18} .\)
The probability that an amateur golfer makes at least one hole in a round is\(1 - (1-q)^{18} .\)
Now, let's use these probabilities to calculate the expected number of holes each golfer will make in 5 rounds of golf:
The expected number of holes made by a professional golfer in 5 rounds is 5 times the expected number of holes made in one round, which is \((1 - (1-p)^{18} )\times18.\)
The expected number of holes made by an amateur golfer in 5 rounds is 5 times the expected number of holes made in one round, which is \((1 - (1-q)^{18} )\times18.\)
We can simplify these expressions using the relationship between p and q:
The expected number of holes made by a professional golfer in 5 rounds is \(518(1 - (1-1.2q)^{18} ).\)
The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-q)^{18} ).\)
We can now evaluate these expressions using the values of p and q:
\(p = 1.2q, so q = p/1.2\)
Substituting this into the expressions above, we get:
The expected number of holes made by a professional golfer in 5 rounds is\(518(1 - (1-1.2(p/1.2))^{18} ) = 518(1 - (1-p)^{18} ).\)
The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-p/1.2)^{18} ).\)
Finally, we can evaluate these expressions using the given probabilities:
The expected number of holes made by a professional golfer in 5 rounds is\(518(1 - (1-1.2q)^{18} ) = 518(1 - (1-1.2(0.1))^{18} ) = 40.7.\)
The expected number of holes made by an amateur golfer in 5 rounds is \(518(1 - (1-q)^{18} ) = 518(1 - (1-0.1/1.2)^{18} ) = 1.6.\)
So according to these calculations, we would expect a professional golfer to make about 40.7 holes over 5 rounds of golf with the new club, while an amateur golfer would only make about 1.6
for such more question on probability
https://brainly.com/question/24756209
#SPJ4
what is the range of the function y= 2x + 3 when the domain is {-3, -1, 1}?
Answers
Answer:
Step-by-step explanation:
domain = x
range = y
when the domain is -1
y = 2(-1) - 3
y = -2 - 3
y = -5
range is -5
When the domain is 0
y = 2(0) - 3
y = 0 - 3
y = -3
range is -3
when the domain is 5
y = 2(5) - 3
y = 10 - 3
y = 7
range is 7
The range is { -5, -3, 7 }
Which value is the best estimate for
√
162
Answers
Answer:
12.7
Step-by-step explanation:
1, 5, 4, 7, 3, 7, 9, 2. if the third odd number is greater than 6, multiply 9 by 3; if it is less than 5, divide 18 by 3. the correct answer is
Answers
The Correct answer is 27
Odd number are the numbers that are not multiple 2 and cannot be divided into two parts equally.
For examples: 3 , 5 , 7, 9,11 . . . . .
According to the question,
If the third odd number is greater than 6, multiply 9 by 3; if it is less than 5, divide 18 by 3.
Sequence of the number is 1, 5, 4, 7, 3, 7, 9, 2
where 1 , 5 , 7 , 7 ,9 are odd numbers
The third odd number is 7 which is greater than 6
according to question we have to multiple 9 by 3
= 9 × 3
= 27
To know more Odd number here
https://brainly.com/question/10850080
#SPJ1
is 3:4 and 9:16 equivalent
Answers
So, 3/4 = 3*4 / 4*4 = 12/16
Now, 12/16 > 9/16 i.e. 3/4 > 9/16
So. 3:4 is larger between 3:4 and 9:16.
Answer:
No
Step-by-step explanation:
Equivalent ratios are created by multiplying/ dividing the parts by the same value.
3 : 4 ( multiply both parts by 4 )
= 12 : 16 not 9 : 16
you cut a board into pieces that are 1/3 ft long. If the board is 5 ft how many pieces will you have
Answers
Answer:
b
Step-by-step explanation:
Answer:
15
Step-by-step explanation:
One foot would have 3 1/3 pieces (because 3 * 1/3 = 1) so that means 5 would have 15 pieces (because 3 * 5 = 15)
A box contains 5 red markers, 6 blue markers, and 5 yellow markers. What is known about the probability model for the situation select all correct answers
Answers
The probability model for this situation is a discrete probability model because we are dealing with a finite number of markers in the box.
1. The probability model is based on the three different colors of markers in the box: red, blue, and yellow.
2. There are a total of 16 markers in the box, with 5 red markers, 6 blue markers, and 5 yellow markers.
3. The probability of selecting a marker of a certain color can be calculated by dividing the number of markers of that color by the total number of markers in the box.
4. For example, the probability of selecting a red marker is 5/16, the probability of selecting a blue marker is 6/16, and the probability of selecting a yellow marker is 5/16.
5. Since the probability model is based on a finite number of markers, it is a discrete probability model.
6. The probability of selecting any one marker is independent of the probability of selecting any other marker, assuming that the markers are well-mixed and that the selection process is random.
Learn more about discrete probability model: https://brainly.com/question/17145091
#SPJ11
What is the total surface area of the rectangular prism shown?

Answers
Answer:
128 in^2
Step-by-step explanation:
L * W
16 * 8 = 128 in^2
Watches and bacteria: A group of researchers investigated the contamination of medical personnel watches at a New York hospital, since there is a potential for patient exposure to potentially dangerous bacteria.They sampled watches worn by physicians, physician assistants, and medical students at a teaching hospital in New York. Nearly half (46.6%) of the watches tested harbored microorganisms that can cause illness. By comparison, only one of the 10 watches worn by security guards tested positive for a disease-carrying microorganism. The researchers want to determine if the difference is statistically significant.Which of the following is an appropriate statement of the null hypothesis, H0?A. The proportion of contaminated wrist-watches from medical personnel is the same as the proportion of contaminated wrist-watches from security guards, i.e., H0: p = 46.6%.B. The proportion of contaminated wrist-watches from medical personnel is not the same as the proportion of contaminated wrist-watches from security guards, i.e., H0: p not equal 46.6%.C. The proportion of contaminated wrist-watches from medical personnel is greater than the proportion of contaminated wrist-watches from security guards, i.e., H0: p > 46.6%.
Answers
An appropriate statement of the null hypothesis, H₀ is that: A. The proportion of contaminated wrist-watches from medical personnel is the same as the proportion of contaminated wrist-watches from security guards, i.e., H0: p = 46.6%.
What is a null hypothesis?In Mathematics, a null hypothesis (H₀) can be defined the opposite of an alternate hypothesis (Ha) and it asserts that two (2) possibilities are the same.
For an experiment to test the contamination of medical personnel wrist-watches at a New York hospital, the appropriate null hypothesis and alternative hypothesis would be given by this mathematical expression:
H₀: p = 10.
Ha: p < 10.
In this context, we can logically that the proportion of contaminated wrist-watches would be the same for both sample proportion i.e., H₀: p = 46.6%.
Read more on null hypothesis here: https://brainly.com/question/14913351
#SPJ1
Matthew has n nickels and d dimes. He has a minimum of $1 worth of coins
altogether. Write this situation as an inequality.
Answers
Answer: \(5n + 10d \ge 100\)
===============================================
Explanation:
5n represents the value of all the nickels, where n is the number of nickels. Let's say he had 8 nickels. This would mean 5n = 5*8 = 40 cents is from just the nickels.
The 10d represents the value of all the dimes. For example, if he had d = 2 dimes, then he has 20 cents from those dimes because 10d = 10*2 = 20.
Combining the two expressions leads to 5n+10d as the total value of both types of coins. This total value is in cents. We want this value to be 100 cents or more. This is why we set 5n+10d to be greater than or equal to 100. That's how we arrive to \(5n+10d \ge 100\)
Optionally we can divide each term by 5 to get \(n + 2d \ge 20\) ,but I'll put the other inequality as the answer because it seems more descriptive in my opinion. Keeping 5n shows each nickel is 5 cents, and 10d shows each dime is 10 cents. Something like n+2d loses a bit of its descriptive nature.
The inequality for the given situation is 5n+10d≥100.
Given that, Matthew has n nickels and d dimes. He has a minimum of $1 worth of coins altogether.
What are inequalities?Inequalities are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
We know that,
A nickel is worth 5 cents. A dime is worth 10 cents. A dollar is worth 100 cents.
Now, the inequality 5n+10d≥100
Therefore, the inequality for the given situation is 5n+10d≥100.
To learn more about the inequalities visit:
https://brainly.com/question/20383699.
#SPJ5
Answer soon pls it’s a test

Answers
Answer: A
Step-by-step explanation:
Unit means per 1, there are 4 units. 2.12 divided by 4 is 0.53
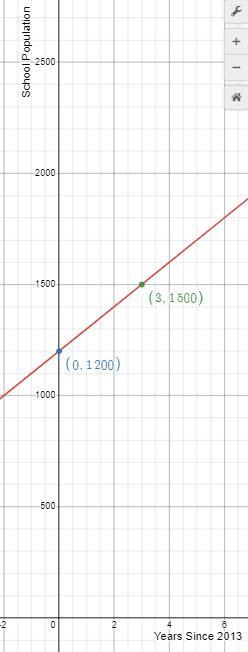
A primary school had 1200 students enrolled in 2013 and 1500 students in 2016.if the students population grows as a linear function of time t,where t is the number of years after 2013.how many will be enrolled in the school in 2020?and find the linear function that relates the students population to time t.
Answers
Answer:
y=100t+1200, where t is years since 2013 and
Step-by-step explanation:
We only have two points from which to form an equation. Since we are told that it is a linear equation, two points is all we need to find an equation in the form of y=mx+b, where m is the slope (the rate of change) and b is the y-intercept (the value of y when x=0). Let's make the x axis the year and y the student population.
Let's put the data into an x,y format, but before we do, lets be sure to adopt the problem's fervent wish that we treat the x variable, t, as the years since 2013. "t is the number of years after 2013." (0,1200) becomes is the data point for 2013. The school's population will be the y-axis.
(0,1200) [primary school had 1200 students enrolled in 2013], and
(3,1500) [1500 students in 2016]
---
First calculate m, the slope. Slope is the Rise/Run between the two points (the change in y over the change in x)
Going from (2013,1200) to (2016,1500) we find that:
Rise (in y) = (1500 - 1200) = 300 students
Run (on x) = (2016 - 2013) = 3 years
The Rise/Run, or slope, m, is 300/3 or 100: m = 100
Lets put that into our equation format:
y = 100x + b
X will be the time, in years. The problem asks that we define x in terms of years after 2013, and that this be assigned the variable, t:
y = 100t +b, where t is years after 2013.
(The 100 tells us that the student population increases by 100 per year)
We now need b, the y-intercept. One can either graph this and look for the value of y when x=0, of simply input either of the data points. This looks easy enough to input a point and solve for b:
Remember that t is the (year - 2013)
y = 100t +b Solve for (2013,1200)
t = 2013 - 2013 = 0
1200 = 100*(0) + b
b = 1200
Actually, b was easy enough to find without either calculating or graphing, since one of our two points tells us the y-intercept (0,1200).
The equation becomes y = 100t + 1200
See the attached graph.