What is the value of the expression?
Drag and drop the answer into the box to match the expression.
0.3(14−1)+0.35
I will give branliest to who gets correct answer
Answers
Answer:
0.3(14-1)+0.35 = 4.25
Step-by-step explanation:
Answer: 4.25 is the answer
Step-by-step explanation:
0.3(14−1)+0.35
=(0.3)(13)+0.35
=3.9+0.35
=4.25
BRANILIIST PLS
Related Questions
a train travels at a speed of 30 mph and travel a distance of 240 miles. how long did it take the train to comlete its journey
Answers
Answer: 8 hours
Step-by-step explanation: 240 mph ÷ 30 = 8 hours
Mackenzie works as a salesperson at an electronics store and sells phones and phone accessories. Mackenzie earns a $10 commission for every phone she sells and a $4 commission for every accessory she sells. On a given day, Mackenzie made a total of $126 in commission and sold 7 more accessories than phones. Write a system of equations that could be used to determine the number of phones sold and the number of accessories sold. Define the variables that you use to write the system.
Answers
Answer:
Let p= the number of phones sold
Let a= the number of accessories sold
Step-by-step explanation:
10p+4a=126
a=p+7
The system of equation should be 10p+4a=126 and a=p+7
Given that,
Mackenzie earns a $10 commission for every phone she sells and a $4 commission for every accessory she sells. On a given day, Mackenzie made a total of $126 in commission and sold 7 more accessories than phones.Based on the above information, the equation is as follows:
Here we assume p= the number of phones sold
And, a= the number of accessories sold
So, the equations are 10p+4a=126 and a=p+7
learn more: https://brainly.com/question/5566317?referrer=searchResults
- 45 × 47 solve using distributive property
Answers
Answer: -2115
Step-by-step explanation:
We can use the distributive property to simplify the calculation of -45 × 47 as follows:
\(\huge \boxed{\begin{minipage}{4 cm}\begin{align*}-45 \times 47 &= -45 \times (40 + 7) \\&= (-45 \times 40) + (-45 \times 7) \\&= -1800 - 315 \\&= -2115\end{align*}\end{minipage}}\)
Refer to the attachment below for explanation
Therefore, -45 × 47 = -2115 when using the distributive property.
________________________________________________________

To solve this problem using the distributive property, we can break down -45 into -40 and -5. Then we can distribute each of these terms to 47 and add the products:
\(\begin{aligned}-45 \times 47 &= (-40 - 5) \times 47 \\ &= (-40 \times 47) + (-5 \times 47) \\ &= -1{,}880 - 235 \\ &= \boxed{-2{,}115}\end{aligned}\)
\(\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}\)
Work out the length of x.
Give your answer rounded to 1 decimal place.
9 m
14.5 m
The diagram is not drawn accurately
Please help

Answers
Answer:
Calculate the value of x. Give your answer ... Hyp. 5.8 m. Opp. 1. Adi. Diagram NOT accurately drawn. POR is a triangle. Angle Q = 90° ... the value of x. Give your answer correct to 1 decimal place. ... a. Diagram NOT accumtely drawn. 9,6 cm. 6.4 cm. A. Hyp. To. Aaj. LMN is a right-angled triangle. MN = 9.6 cm. ... x = ton-14.5.
Step-by-step explanation:
please be right
Sheena made a scale drawing of her classroom using a scale of 1 inch = 10 feet. One wall of the classroom in the drawing is 4 inches long. Which proportion can be used to findx, the length of the actual wall, in feet?
Answers
The proportion that can be used to find the length of the actual wall, in feet, is x/4 inches = 10 feet/1 inch.
Given that Sheena made a scale drawing of her classroom with a scale of 1 inch = 10 feet, and the length of the wall in the drawing is 4 inches, we can set up a proportion to find the length of the actual wall in feet.
Let x represent the length of the actual wall in feet.
Using the scale of the drawing, we can set up the following proportion:
x feet / 4 inches = 10 feet / 1 inch
To solve for x, we can cross-multiply and solve the resulting equation:
x feet * 1 inch = 4 inches * 10 feet
x = (4 inches * 10 feet) / 1 inch
x = 40 feet
Therefore, the proportion that can be used to find the length of the actual wall, in feet, is x/4 inches = 10 feet/1 inch.
Learn more about proportions and scale drawings here: brainly.com/question/12100213
#SPJ11
Henry measured the lengths of his three surfboards at 6 feet 8 inches, 5 feet 10 inches, and 6 feet 4 inches. Writing the inches as fractions, list the lengths of the boards in order from longest to shortest.
Answers
The length can be listed in order from longest to shortest.
How can we convert all the measurements to a common unit?First, we need to convert all the measurements to a common unit. We can choose feet or inches, but let's convert everything to inches to avoid working with mixed units.
6 feet 8 inches = (6 x 12) + 8 = 80 inches
5 feet 10 inches = (5 x 12) + 10 = 70 inches
6 feet 4 inches = (6 x 12) + 4 = 76 inches
Now we can list the lengths in order from longest to shortest:
80 inches > 76 inches > 70 inches
So the order from longest to shortest is:
6 feet 8 inches > 6 feet 4 inches > 5 feet 10 inches
Learn more about measurements
brainly.com/question/4725561
#SPJ11
Help me pls. Graphing Using Slope. Look at the pictures



Answers
Answer:
answers attached
Step-by-step explanation:



A student flips a coin three times. What is the probability the coin lands tails up exactly two times?
Answers
Answer:
1:3
Step-by-step explanation:
I believe this would be right
The probability the coin lands tails up exactly two times is 3/8
How to determine the probability?When a coin is flipped three times, the sample space is;
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
In the above sample space, there are 3 occurrences where the coin lands tail up, out of the 8 occurrences.
So, the probability is:
P = 3/8
Hence, the probability the coin lands tails up exactly two times is 3/8
Read more about probability at:
https://brainly.com/question/25870256
#SPJ2
GUYS...HELP ME WITH THIS...WILL GIVE BRAINLIEST...
solve for x .....
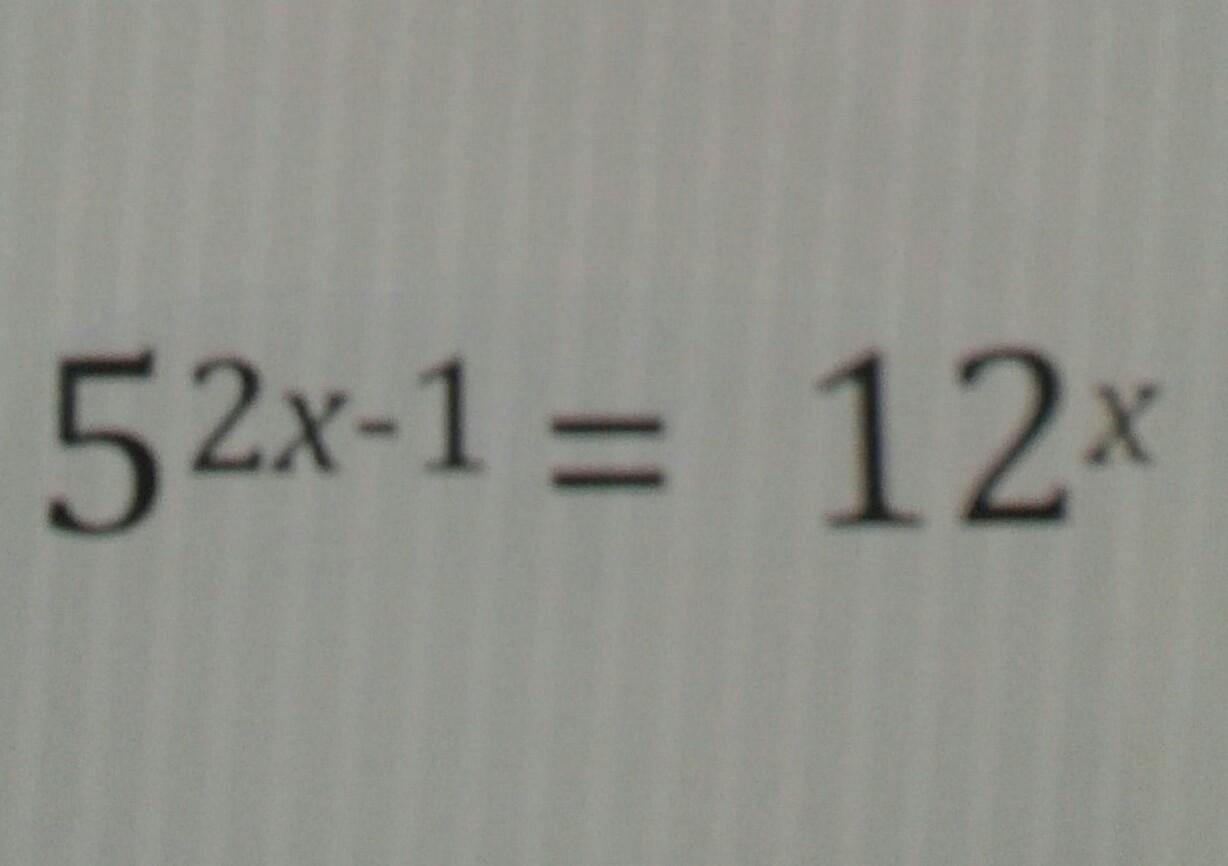
Answers
Answer:
2.19
Step-by-step explanation:
\( {5}^{2x - 1} = {12}^{x} \\ \\ taking \: log \: on \: both \: sides \\ \\ log {5}^{2x - 1} = log {12}^{x} \\ \\ (2x - 1)log {5} = x \: log \: 12 \\ \\ 2x \: log \: 5 - log \: 5 = x \: log \: 12 \\ \\ x \: log \: 5 ^{2} -x \: log \: 12 = log \: 5 \\ \\ x \: (log \: 25 -log \: 12) = log \: 5 \\ \\ \\ x = \frac{log \: 5 }{(log \: 25 -log \: 12) } \\ \\ x = \frac{0.698970004}{1.39794001 -1.07918125 } \\ \\ x = \frac{0.698970004}{0.318758763 } \\ \\ x = 2.19278679 \\ \\ x \approx 2.19\)
Just answer with the value to put in the box thanks !

Answers
Answer:
x = 10.8
Step-by-step explanation:
9 ÷ x = x ÷ (9 + 4)
9 × (9 + 4) = x × x
9 × 13 = x²
117 = x²
x = 10.81665383
I've been stuck on this for 7 minutes please help me

Answers
Answer:
P(green or red) = 935/2721
P(blue, red, or yellow) = 409/907
P(not brown) = 2236/2721
P(not green) = 2171/2721
Step-by-step explanation:
Probability in this problem can be represented by the ratio:
\(\dfrac{\text{part}}{\text{whole}}\)
We can apply this to the first question:
The probability of choosing a green or red M&M can be represented with:
\(\dfrac{\# \text{ of red and green M}\& \text{Ms}}{\text{total } \# \text{ of M}\& \text{Ms}}\)
(Note: '#' means 'number')
We can fill this ratio in with the values given in the table.
\(\dfrac{385 + 550}{2721}\)
This simplifies to:
\(\dfrac{935}{2721}\)
So, the probability of choosing a green or red M&M is 935/2721.
⎯⎯
We can apply this same concept to the rest of the questions.
test the series for convergence or divergence. 4 5 − 4 7 + 4 9 − 4 11 + 4 13 −
Answers
Therefore, the series 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - ... is convergence in nature.
To test the convergence or divergence of the given series: 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - ..., we can use the alternating series test. The alternating series test states that if a series has the form (-1)^n b_n, where b_n is a positive sequence that is decreasing and approaches zero as n approaches infinity, then the series converges.
In the given series, we have b_n = 4/(2n+3), which is a positive sequence that approaches zero as n approaches infinity. To see that b_n is decreasing, we can note that b_{n+1}/b_n = 2(2n+3)/(2n+5) < 1 for all n, since the numerator is always less than the denominator. Therefore, b_n is a positive, decreasing sequence that approaches zero as n approaches infinity.
Furthermore, the series has the form (-1)^n b_n, where the sign alternates between positive and negative. Therefore, we can apply the alternating series test, which tells us that the series converges.
To know more about convergence,
https://brainly.com/question/20876952
#SPJ11
the obtained value must be compared against which of the following? a. test value b. critical value c. expected value
d. observed value
Answers
The obtained value must be compared against the critical value. Hence, the correct option is b.
In hypothesis testing, the critical value is a threshold or cutoff point that is determined based on the chosen significance level (alpha level) and the distribution of the test statistic. It helps in determining whether to reject or fail to reject the null hypothesis.
After calculating the test statistic (such as z-score or t-statistic) from the observed data, it is compared to the critical value associated with the chosen significance level.
If the test statistic exceeds the critical value, it falls into the critical region, leading to the rejection of the null hypothesis.
If the test statistic is less than or equal to the critical value, it falls into the non-critical region, resulting in a failure to reject the null hypothesis.
Therefore, the obtained value must be compared against the critical value to make a decision in hypothesis testing. Hence, the correct answer is option b.
To know more about critical value refer here:
https://brainly.com/question/32389590#
#SPJ11
Lottie and Ollie shared some money in the ratio 5:1.
Ollie received £15.
How much did Lottie receive?
Answers
Answer:
=£75
Step-by-step explanation:
ratio=5(lottie):1(Ollie)
we do 15/1 which will stay the same as 15
15/1=15
Then we times 15 by 5( lotties share)=75
15*5=75
Therefore lottie got £75
=£75
Answer:
75 : 15
Step-by-step explanation:

Indicate below weather the equation in the box is true or false

Answers
Answer:
False
Step-by-step explanation:
4/8 equals to 1/2 but 6/10 equals to 3/5. Correct would be if it was 5/10
the 14c:12c ratio can be used to date fossils that are up to approximately how old?
Answers
The 14C:12C ratio can be used to date fossils that are up to approximately 50,000 years old. This is because the half-life of carbon-14 (14C) is about 5,730 years, which limits its effective dating range.
In summary, the 14C:12C ratio is used to date fossils that are up to approximately 50,000 years old due to the half-life of carbon-14 (14C).
Carbon-14 is a radioactive isotope of carbon that is formed in the upper atmosphere through the interaction of cosmic rays with nitrogen-14. It is incorporated into the carbon cycle and taken up by living organisms through photosynthesis or consumption of other organisms. While an organism is alive, the 14C:12C ratio remains relatively constant. However, once the organism dies, it no longer takes in carbon-14, and the 14C atoms in its remains undergo radioactive decay. By measuring the 14C:12C ratio in a fossil sample and comparing it to the 14C:12C ratio in the atmosphere at the time of death, scientists can estimate the age of the fossil. However, the effectiveness of carbon-14 dating diminishes as the age of the sample exceeds around 50,000 years, as the amount of remaining carbon-14 becomes too small to accurately measure.
To learn more about radioactive isotope click here, brainly.com/question/28039996
#SPJ11
What is the slope-intercept equation for the linear function represented by the
table?

Answers
Answer: y= 3/2x - 6
Step-by-step explanation:
The equation is y=mx + b
The y-intercept is when x = 0, so on the table y-intercept = -6
The slope is rise/run, we see that y increase by three and x increase by 2, so the slope is 3/2
to get the slope of any straight line, we simply need two points off of it, let's use those ones in the picture below.
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{-3})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{3}-\stackrel{y1}{(-3)}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{2}}} \implies \cfrac{3 +3}{4} \implies \cfrac{ 6 }{ 4 } \implies {\Large \begin{array}{llll} \cfrac{3 }{ 2 } \end{array}}\)
now, the y-intercept occurs when x = 0, recheck the picture below.

Solve for x:-
\(\sf -10 + x + 4 - 5 = 7x - 5\)
Answers
Answer:
x = -1
Step-by-step explanation:
Now we have to,
→ find the required value of x.
The equation is,
→ -10 + x + 4 - 5 = 7x - 5
Then the value of x will be,
→ -10 + x + 4 - 5 = 7x - 5
→ -11 + x = 7x - 5
→ 7x - x = -11 + 5
→ 6x = -6
→ x = -6/6
→ [ x = -1 ]
Hence, the value of x is -1.
A wire is attached to the top of a tower and to a point on the ground that is 35 m from the base of the tower. If the wire makes a 65 degree angle with the ground, how long is the wire? Round your answer to the nearest tenth.
Answers
Answer:
83
Step-by-step explanation:
The length of the wire is 83meter.
Given that,
A wire is attached to the top of a tower and to a point on the ground that is 35 m from the base of the tower.
If the wire makes a 65-degree angle with the ground.
We have to determine,
How long is the wire?
According to the question,
The computation of the length of the wire is shown below:
Let, the length of the wire be x,
There is 35m from the base of the tower,
And, the angle with the ground is 65 degree
Therefore,
The length of the wire is given by,
\(cos65 = \dfrac{35}{x}\\\\\)
Substitute the value of cos65 in the equation,
\(cos65 = \dfrac{35}{x}\\\\x = \dfrac{35}{cos65}\\\\x = \dfrac{35}{0.42}\\\\x = 83.33 \ meter\)
Hence, The length of the wire is 83meter.
To know more about Trigonometry click the link given below.
https://brainly.com/question/14418346
Which part of the merge sort is accomplished with recursion?
a. Recursion is used to break the list down repeatedly until it gets to one element.
b. Recursion is used to find the correct order of each element.
c. Recursion is used to put the elements back together once they are broken apart.
d. Recursion is used to determine if the list needs to be sorted.
Answers
The part of the merge sort that is accomplished with recursion is option a, where recursion is used to break the list down repeatedly until it gets to one element.
Merge sort is a divide-and-conquer algorithm, where the original list is divided into smaller sublists until each sublist contains only one element. This process is accomplished through recursive calls, where the function is called repeatedly on smaller sublists until each sublist contains only one element.
Once the sublists are reduced to single elements, the merge sort algorithm uses another recursive function to merge the sublists back together in sorted order.
Recursion is not used to find the correct order of each element, as this is accomplished during the merging phase. Similarly, recursion is not used to determine if the list needs to be sorted, as merge sort is always used to sort a list.
Learn more about recursion here:
https://brainly.com/question/30063488
#SPJ4
Answer:
Recursion is used to break the list down repeatedly until it gets to one element.
Step-by-step explanation:

Simplify a raised to the negative third power over quantity 2 times b raised to the fourth power end quantity all cubed
Answers
Here is the answer
I hope it helped you

After drinking, the body eliminates 37% of the alcohol present in the body per hour.
a) The amount of alcohol in grams in the body on an hourly basis is described by a discrete time dynamical system (DTDS) of the form xn+1=f(xn), where xn is the number of grams of alcohol in the body after n hours. Give the updating function f (as a function of the variable x).
b) Peter had three alcoholic drinks that brought the alcohol content in his body to 41 grams, and then he stopped drinking. Give the initial condition (in grams) for the DTDS in (a).
c) Find the solution of the DTDS in (a) with the initial condition given in (b). (Your answer will be a function of the variable n, which represents time in hours.)
Answers
The solution of the DTDS is xn = (0.63)^n * 41 grams, where n represents time in hours.
a) The updating function f(x) for the discrete time dynamical system (DTDS) can be derived from the given information that the body eliminates 37% of the alcohol present in the body per hour.
Since 37% of the alcohol is eliminated, the amount remaining after one hour can be calculated by subtracting 37% of the current amount from the current amount. This can be expressed as:
f(x) = x - 0.37x
Simplifying the equation:
f(x) = 0.63x
b) The initial condition for the DTDS is given as Peter having 41 grams of alcohol in his body after consuming three alcoholic drinks. Therefore, the initial condition is:
x0 = 41 grams
c) To find the solution of the DTDS with the given initial condition, we can use the updating function f(x) and iterate it over time.
For n hours, the solution is given by:
xn = f^n(x0)
Applying the updating function f(x) repeatedly for n times:
xn = f(f(f(...f(x0))))
In this case, since the function f(x) is f(x) = 0.63x, the solution can be written as:
xn = (0.63)^n * x0
Substituting the initial condition x0 = 41 grams, the solution becomes:
xn = (0.63)^n * 41 grams
Learn more about function at: brainly.com/question/30721594
#SPJ11
a count went up from 450 to 600. what was approximate percentage increase?
Answers
Please help me all I need is 41,42,43. Also could u friend me I just sighned up

Answers
Answer:
trailing zeros are dropped1846 beats42×(selling price for 1 tin)Step-by-step explanation:
41. The product of 0.25 and 0.4 is 0.100, with three decimal places. Trailing zeros are usually dropped--except when they are used to indicate significant digits in a calculation. Hence, the usual presentation of the result is ...
0.25 × 0.4 = 0.1
__
42. To find total beats, multiply beats per second by seconds.
(52 beats/second)(35.5 seconds) = (52)(35.5) beats = 1846 beats
The hummingbird's wings will beat 1846 times in 35.5 seconds.
__
43. To find total sales for the week, multiply the price of a tin of popcorn by the number sold in the week (42).
Answer:
41) 0.25 × 0.4 = 0.1
It has only one decimal place in the product because 0.25 has two significant figures and 0.4 has one significant figure. When multiplying, the product will always match with the number that has the least amount of significant figures. Since 0.4 has one significant figure, the product, 0.1, will also have one significant figure.
42) 35.5 s × 52 times/s = 1,846 times
43) 42 tins × $9.25/tin = $388.50
Hope that helps.
The sides of a triangle are (x + 3) cm, (2x - 1) cm, and (3x + 4) cm. What is the perimeter of the triangle? *
Answers
Answer:
Step-by-step explanation:
Perimeter is all sides added together...
X+3+2x-1+3x+4
Combine like terms
X+2x+3x.. 6x
3-1+4.. 2+4.. 6
Answer:
6x+6
PLEASE HELP! I’m not sure if i’m right

Answers
Answer:
looks right
Step-by-step explanation:
Answer:
you are correct
Step-by-step explanation:
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.


Answers
We are given two plots of normal distributions A and B.
The mean of a normal distribution is located at the center of the plot.
Since the centers of both of the normal distributions A and B seems to be aligned, therefore, they both seems to have equal means.
The standard deviation basically determines the shape of the distribution.
As you can see, the normal distribution A is more spread out and thus has a larger standard deviation than normal distribution B.
Therefore, the two correct options are
• The means of A and B are equal.
,• A has larger standard deviation.
a recent survey found that out of a random sample of 150 drivers, 100 of them wear seatbelts. what is the 95onfidence interval for the proportion p of drivers that do not wear seatbelts?
Answers
The 95% CI for proportion of driver that do not wear seat belt is 0.255 < p < 0.405.
What is Confidence interval?
A confidence interval (CI) is a range of estimates for an unknown parameter in frequentist statistics. The 95% confidence level is the most popular, however other levels, such 90% or 99%, are occasionally used when computing confidence intervals.
As given,
n = 150 = drivers
x = 100 = wear seat belts.
We have to find 95% confidence interval for proportion P that do not wear seat belt.
From 150 we have 100 wear seat belts
Not wear seat belt = 150 - 100
Not wear seat belt = 50
P = 50/150
P = 0.33
95% confidence interval for P is
CI = (P - zα/2√(P(1 - P)/n), P + zα/2√(P(1 - P)/n))
For 95% CI, zα/2 = 1.96
Substitute values,
CI = (0.33 - 1.96√(0.33(1 - 0.33)/150), 0.33 + 1.96√(0.33(1 - 0.33)/150))
CI = (0.33 - 0.075, 0.33 + 0.075)
CI = (0.255, 0.405)
Therefore 95% CI for proportion of driver that do not wear seat belt is 0.255 < p < 0.405.
To learn more about Confidence interval CI from the given link.
https://brainly.com/question/20309162
#SPJ4
Using the information in the diagram determine the height of the tree

Answers
Given
To find the height of the tree.
Explanation:
It is given that,
From the figure, it is clear that ΔABC and ΔADE.
That implies,
\(\begin{gathered} \frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC} \\ \frac{x}{2x}=\frac{y}{2y}=\frac{DE}{200} \\ \frac{1}{2}=\frac{DE}{200} \\ DE=\frac{200}{2} \\ DE=100 \end{gathered}\)Hence, the height of the tree is 100ft.


please just find the measures of the segment plzzzzzzzz

Answers
Answer:
BE=19 AD=29
Step-by-step explanation: