what is the square root of 149 rounded to the nearest hundredth?
Answers
149 rounded to the nearest hundredth is 12.2
Solve: Square root of 149 rounded to the nearest hundredth's.
Solution:
The square root of 149 cannot be simplified. √149 is already in its simplest radical form.
The square root of 149 is 12.2065556157
Rounding that number to the nearest tenth is equals to 12.2
Therefore, 149 rounded to the nearest hundredth is 12.2
Related Questions
Suppose an annuity pays 6% annual interest, compounded semi-annually. You invest in this annuity by contributing $4,500 semiannually for 6 years. What will the annuity be worth after 6 years? Assume that the annuity is compounded with the same frequency as deposits are made unless stated otherwise.
Answers
The annuity that should be worth after 6 years is $63,900.
Given that,
The present value is $4,500.The semi-annual time period should be = 6 × 2 = 12.The rate of interest on semi-annual basis should be = 6% ÷ 2 = 3%Now the following formula should be used:
\(Amount = Present\ value \times \frac{(1+ rate)^{(n)} - 1} {rate}\\\\= \$4,500 \times \frac{(1+0.03)^{12} - 1}{0.03}\\\\= \$4,500 \times \frac{0.4257}{0.03}\\\\= \$4,500 \times 14.1920\\\\= \$63,864\\\\= \$63,900\)
Therefore we can conclude that the annuity that should be worth after 6 years is $63,900.
Learn more about the annuity here: brainly.com/question/17096402
Answer: 63900
Step-by-step explanation: Use the savings annuity formula
PN=d((1+r/k)N k−1)r/k
to calculate the value of P6. The question states that r=0.06, d=$4,500, k=2 compounding periods per year, and N=6 years. Substitute these values into the formula results in
P6=$4,500 ((1+0.06/2)6⋅2−1)/(0.06/2).
Simplifying, we have P6=$4,500 ((1.03)12−1)/(0.03). Therefore P6=$63,864.13. Our final answer is 63900.
PLS HELP ASAP I WILL GIVE 50 POINTS AND BRAINIEST IM DESPERATE !!!!
A regular pentagon and a regular hexagon are both inscribed in the circle below, Which shape has a bigger area? explain your reasoning.
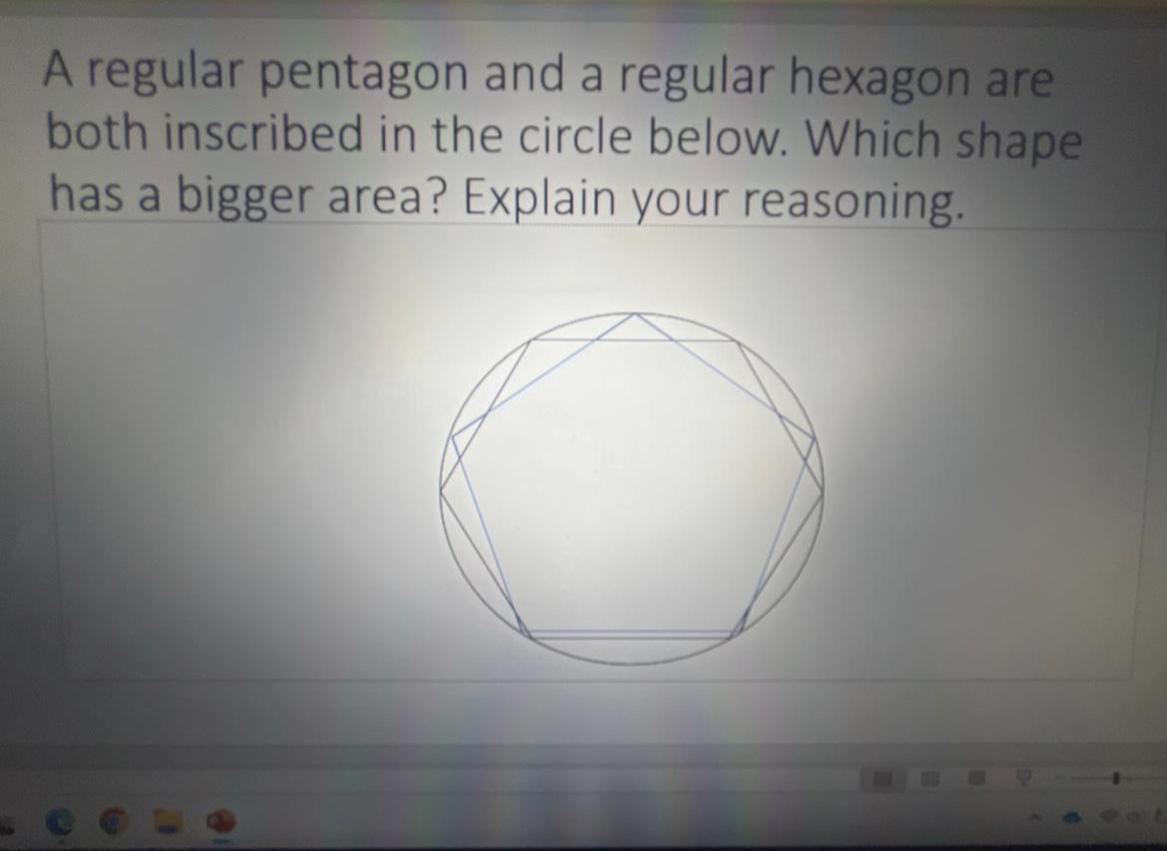
Answers
The shape that has a bigger area is the regular hexagon.
Which shape has a bigger area?The shape that has a bigger area is the regular hexagon. A hexagon is a polygon with six sides while a pentagon is a polygon with five sides. The area of a polygon measures the surface of the shape.
The polygon with six sides has a greater surface so it is expected that its area will be bigger than that of the pentagon with fewer sides.
Learn more about regular pentagons here:
https://brainly.com/question/858867
#SPJ1
When a = 1 and b = 5, what is the value of c?
Answers
Answer:
5.1
Step-by-step explanation:
a² + b² = c²
1² + 5² = c²
1 + 25 = c²
26 = c²
c = 5.1
Answer:
The constant of variation is k =
3/8
When a = 1 and b = 5, what is the value of c?
3/40
what is f(x)=0
what does it equal too
Answers
Answer:
x=1 at f(x)=0
Step-by-step explanation:
When graphing the function, always try to remember that f(x) is almost the same as saying 'y'. Then find the point that corresponds on the graph where y=0, which is x=1.
For the parabola y = (x+14)^2 -4, The value of the y coordinate of the vertex is?
Answers
Answer:
-4
Step-by-step explanation:
y = (x+14)^2 -4
The equation is in vertex form
y = a(x-h)^2 + k where (h,k) is the vertex
The y coordinate of the vertex is k = -4
Answer:
y - coordinate = - 4
Step-by-step explanation:
The equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is a multiplier
y = (x + 14)² - 4 ← is in vertex form
with vertex = (- 14, - 4 )
The y- coordinate of the vertex = - 4
What is the solution to the system of equations y equals 1.5 x minus 4y equals negative x?
Answers
The solution to the system of equations is (1.6,-1.6).
What is the system of equations?
Two or more equations in algebra must be solved jointly (i.e., the solution must satisfy all the equations in the system). The number of equations must match the number of unknowns for a system to have a singular solution.
Here, we have
Given equations:
y = 1.5x - 4....(1)
y = -x....(2)
Substitute y = -x in the first equation
-x = 1.5x - 4
Collect like terms
-1.5x - x = -4
This gives
-2.5x = -4
Divide both sides by -2.5
x = 1.6
Substitute x = 1.6 in y = -x
y = -1.6
Hence, the solution to the system of equations is (1.6,-1.6)
To learn more about the system of equations from the given link
https://brainly.com/question/28405823
#SPJ4
Answer my math question I asked so many times I lost most of points by

Answers
Write a brief statement about life in the mid-1800s using the following terms. A. Prejudice B. Discrimination C. Famine d. Nativists e. Emigrant
Answers
Answer:
Step-by-step explanation:
Life in the mid-1800s was marked by widespread prejudice and discrimination against minority groups, including immigrants and African Americans. The period was also characterized by a series of famines that led to significant suffering and mortality. Nativist movements gained popularity, promoting the interests of those born in the United States over those of immigrants. At the same time, millions of emigrants left their homes in search of better opportunities in America, despite the obstacles they faced upon arrival.
Answer:
(if you would like a short one/ still need help)
Nativists we’re prejudice and discriminatory towards Irish emigrants who had come to the United States after the events of the Irish Potato Famine
hope this helps :)
Can someone please help me

Answers
Answer:
1. a=3
2. a=3
3. a=9
Step-by-step explanation:
1. 9/a+9-4=12-56/8+3
We move all terms to the left:
9/a+9-4-(12-56/8+3)=0
Domain of the equation: a=0
a∈R
We add all the numbers together, and all the variables
9/a+9-4-8=0
We add all the numbers together, and all the variables
9/a-3=0
We multiply all the terms by the denominator
-3*a+9=0
We add all the numbers together, and all the variables
-3a+9=0
We move all terms containing a to the left, all other terms to the right
-3a=-9
a=-9/-3
a=+3
Find the midpoint of the line segment AB if A = (7, 2) and B = (5, -4). ( with photo pls)
Answers
Answer:
(6, -1)
Step-by-step explanation:
The midpoint formula, (y2+y1)/2 and (x2+x1)/2 will help us find our answer. So (2-4)/2= -1 and (7+5)/2=6, so (6,-1) is the midpoint of segment AB.
Identify the formula to calculate the number of bit strings of length six or less, not counting the empty string. a. Σ7i = 02i b. Σ6i = 02i c. Σ6i = 02i d. (Σ7i = 02i) - 1
Answers
The formula to calculate the number of bit strings of length six or less, not counting the empty string, is (Σ6i=0 2i) - 1.
To explain this formula, let's break it down. The Σ6i=0 represents a summation from i=0 to i=6. The 2i represents the number of possibilities for each bit (either 0 or 1) and the summation allows us to count all possible combinations of bit strings of length 6 or less.
However, we need to subtract 1 from the total because we are not counting the empty string. This formula ensures that we are only counting bit strings with at least one bit set to either 0 or 1.
In simpler terms, the formula tells us to take 2 to the power of each possible bit position (from 0 to 6), add up all those possibilities, and then subtract 1 to account for the empty string. This gives us the total number of possible bit strings of length six or less.
To know more about strings refer here
https://brainly.com/question/30099412#
#SPJ11
Light travels at a rate of about 9,460,528,400,000,000 m per year.
Choose the best approximation of how many meters light travels per year.
Choose 1 answer:
(A) 9x10^15
(B) 9x10^16
Answers
Answer:
A
Step-by-step explanation:
You just find out which number is closer to the speed of light
Answer:
9x10^15
Step-by-step explanation:
9,460,528,400,000,000
If you count the numbers up until 9 you get 15. So the easy hack is to just count the numbers up until the VERY first then whichever answer had that number is the right one.
Determine whether the function is a polynomial function. If it is a polynomial function, then state the degree and leading coefficient.

Answers
The polynomial function is h(x)=\(\sqrt[3]{64x^{3} +27x^{6} }\). The degree of the polynomial is 6 and the leading coefficient is 27.
Given that,
The polynomial function is h(x)=\(\sqrt[3]{64x^{3} +27x^{6} }\)
We have to analyze the function to see if it is a polynomial function. State the degree and leading coefficient if the function is a polynomial.
The sum of one or more terms, each of which is either a number or a number multiplied by the independent variable and raised to a positive integer exponent, is known as a polynomial function.
The exponent of the variable, or zero if there is no variable, determines a term's degree.
The biggest term degree is the polynomial of the Function.
The Distributive Property is used to join terms having the same Degree.
Usually, terms are presented in order of decreasing Degree.
An nth degree polynomial function of x is often stated as follows:
F(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + aₙ₋₂xⁿ⁻² +... + a₁x + a₀
So,
h(x)=\(\sqrt[3]{64x^{3} +27x^{6} }\)
Therefore, the degree of the polynomial is 6 and the leading coefficient is 27.
To learn more about polynomial visit: brainly.com/question/11536910
#SPJ1
two independent samples of sizes 20 and 25 are randomly selected from two normal populations with equal variances. in order to test the difference between the population means, the test statistic is:
Answers
To test the difference between the population means, the test statistics we use is t-test.
According to the question we have been given that,
There are two independent samples of sizes 20 and 25.
The population is normally distributed and have equal variances.
We have to test the difference between the population means. For that the test statistics we will use is t- test.
t - test is used when we have to compare the means of two groups and how they are related. Also the sample size should be less than 30 (<30)
Learn more about t-test here :https://brainly.com/question/17205773
#SPJ4
A researcher plans to study the causal effect of police crime using data from a random sample of U.S. counties. He plans to regress the county's crime rate on the (per capita) size of the country's police force. Why is this regression likely to suffer from omitted variable bias? A. Other regressors are likely perfectly collinear with the (per capita) size of the county's police force, so they should be included in the regression B. There are other important determinants of a country's crime rate, including demographic characteristics of the population, that if left out of the regression C. There are other important determinants of a country's crime rate, including demographic characteristics of the population, that if left out of the regression D. None of the above are correct
Answers
Answer:
Step-by-step explanation:B
Simplify a+a+a+a+a+a
Answers
Answer:
a+a+a+a+a+a= 6a
Step-by-step explanation:
brainliest???
Jeff ran 6 miles in 4 hours. At this rate, how many miles will he run in 6 hours
Answers
Answer:
he ran 9 miles in 6 hours
Step-by-step explanation:
trust me
pls mark me as brainliest
9 mi
Step-by-step explanation:
Step 1. Calculate the rate.
rate = distance/time
r = d/t = 6 mi/4 h
===============
Step 2. Calculate the time.
r = d/t Multiply both sides by t
d = tr
t = 6 h Calculate the distance
d = 6 × 6/4
d = 36/4
d = 9 mi
Jeff will run 9 mi in 6 h.
how to do this question plz answer me step by step plzz plz

Answers
Answer:
2 Pi
Step-by-step explanation:
Notice that the shape is made of:
● 1 square with a side of 1 meter length
● 4 half-circles wich means 2 cicles with a diameter lf 1 meter.
■■■■■■■■■■■■■■■■■■■■■■■■■■
The square is inside so it isn't necessary to calculate the perimeter.
The perimeter of a circle is:
P' = d × Pi
We have 4 half-squares wich means two circles
So the total perimeter is:
● P = 2×P'
● P = 2 × d × Pi
● P = 2 × 1 × Pi
● P = 2Pi
let f(x) = 3/3-× and g (×) = 11+x find the domain of (f/g) (x)

Answers
Answer:
\(\lbrace x|x\text{ is a real number and x }\ne\text{ -11},3\rbrace\)Explanation:
Here, we want to get the domain of the given function
We start by dividing the two as follows:
\((\frac{f}{g})(x)\text{ = }\frac{f(x)}{g(x)}\)\(\begin{gathered} So,\text{ we have it that:} \\ \frac{3}{3-x}\times\frac{1}{11+x}\text{ = }\frac{3}{33+3x-11x-x^2}\text{ = }\frac{3}{33-8x-x^2} \end{gathered}\)The domain refers to the possible x-values
To get that, we need to solve the quadratic equation in the denominator
We have that as:
\(\begin{gathered} 33-8x-x^2=0 \\ 33-11x+3x-x^2=0 \\ 11(3-x)+x(3-x)=\text{ 0} \\ (11+x)(3-x)\text{ = 0} \\ x\text{ = -11 or 3} \end{gathered}\)So, we have the domain as:
\(\mleft\lbrace x|x\text{ is a real number and x }\ne\text{ -11},3\mright\rbrace\)Pls help I need a lot ive failed this 3 times I can't fail again ahhh please help

Answers
Answer:
B.) and C.)
Step-by-step explanation:
Figure can be cut in half = reflection symmetry
Figure can be flipped = 180 rotational symmetry
(if those four choices in the picture are the only choices)
12 Katy and Ross tutor math students. The table below shows the amount
of money they collected each week for four weeks
vo
WEEKLY MONEY COLLECTED
Week Money Collected (m)
1
2
3
4
$450
$510
$600
$480
If they tutored a total of 136 students, which equation represents the
relationship between the money collected (m) and the number of
students tutored (x)?
(Don’t mind the doodles)

Answers
Answer: I believe the answer is A.
Step-by-step explanation: Sorry if it's wrong.
Julius sells two robots a small one and a larger model. the price for the smaller robot is X and the price for the large robot is Y. write an equation that will let him earn a profit of $13,050 if he sells 15 small robots and 42 large robots.
Answers
Answer:
15x + 42y = $13 050
Step-by-step explanation:
hope that helped :)
need help on this equation

Answers
Answer:
x =1Step-by-step explanation:
Given the following DE = 4X-2
EF = 3x+2
FG 5x-3
GD = 2x+5
Since DE is parallel to GF, this means that the sides are equal hence;
4x - 2 = 5x - 3
4x - 5x = -3 + 2
-x = -1
x = 1
Hence the value of x is 1
Can anyone help me with this question please ?

Answers
Answer:
-0.20412414523 there you go
jessica has four small boxes that are the same size and one large box. Each of the four small boxes is 4 centimeters wide and 2 centimeters long. The large box has a volume of 96 cubic centimeters. jessica puts the four small boxes into the large box. there’s no space leftover.
What is the height of the one small box?
Answers
Answer:
H = 3
Step-by-step explanation:
V of Large box = 4 x (V of Small box)
96/4 = 24
24 = V Small box.
V = L x W x H
24 = 2 x 4 x H
24 = 8 x H
3 = H
Therefore height of small box is 3.
The height of the one small box is 4 cm if Jessica puts the four small boxes into the large box. there’s no space leftover.
What is a cuboid?It is defined as the six-faced shape, a type of hexahedron in geometry.
It is a three-dimensional shape.
Jessica has four small boxes that are the same size and one large box.
The dimensions for the small boxes:
Width w = 4 cm
Length l = 2 cm
Volume of a large box = 96 cubic centimetres
As Jessica puts the four small boxes into the large box. there’s no space leftover, mathematically,
The volume of the large box = 4(Volume of the small boxes)
The volume of the large box = 4(l×w×h)
Where h is the height of the small box.
96 = 4(3×2×h)
24h = 96
h = 4 cm (divide by 48 on both sides)
Thus, the height of the one small box is 4 cm if Jessica puts the four small boxes into the large box. there’s no space leftover.
Learn more about the cuboid here:
brainly.com/question/9740924
a helpful rule for converting radians to degrees is
Answers
Answer:
Degrees = Radians x 180/π
or
Degrees = 57.2958 x radians
Step-by-step explanation:
1 radian = 180/π degrees
1 radian = 57.2958 degrees
Multiply radians by this factor of 57.2958 to get the equivalent measure in degrees
π radians = 180°
2π radians = 360° which is the number of degrees in a circle
For anything greater than 2π radians you will have to subtract 360°
For example, 7 radians using the formula is 7 x (57.2958 ) ≈ 401.07°
But this still falls in the first quadrant, so relative to the x-axis it is
401.07 - 360 = 41.07°
1. Which of the following is a rational number? (4 points)
197, 198, 199, 100
197
198
199
V100

Answers
Answer:
\(the \: rational \: number \: is \: \sqrt{100} \)
Step-by-step explanation:
The reason why
\( \sqrt{97} \)
isn't a rational number is because, when simplified, it results in 9.848857802.... its decimal doesn't terminate(stop).
The reason why
\( \sqrt{98} \)
isn't a rational number is because, when simplified, it results in 9.899494937.... it's decimal doesn't terminate(stop).
The reason why
\( \sqrt{99} \)
isn't a rational number is because, when simplified, it results in 9.949874371.... it's decimal doesn't terminate(stop).
The reason why
\( \sqrt{100} \)
is a rational number is because, when simplified, it results in 10, its decimal terminates (stops).
A quantity with an initial value of 8500 grows exponentially at a rate such that the quantity doubles every 9 years. What is the value of the quantity after 23 years, to the nearest hundredth?
Answers
Answer: We can use the formula for exponential growth to find the value of the quantity after 23 years:
Q(t) = 8500 * 2^(t/9)
Where Q(t) is the value of the quantity after t years, and t/9 is the number of doublings that have occurred.
Substituting t = 23 into the formula:
Q(23) = 8500 * 2^(23/9) = 8500 * 2^2.56 = 8500 * 12.90 = 109350
So, after 23 years, the quantity has a value of approximately 109,350, rounded to the nearest hundredth.
Step-by-step explanation:
someone smart please help me

Answers
Answer:
It would be the fourth option.
Step-by-step explanation:
Hope this helps:)
Simplify: (9x^3+2x^2-5x+4)-(5x^3-7x+4)
Show all steps used to solve this problem and write your final answer in factored form in the space provided.
Answers
To simplify (9x^3+2x^2-5x+4)-(5x^3-7x+4), we can start by combining like terms.
First, we need to distribute the negative sign to the second set of parentheses:
(9x^3+2x^2-5x+4) - 1(5x^3-7x-4)
= 9x^3 + 2x^2 - 5x + 4 - 5x^3 + 7x - 4 (distributing the negative sign)
= (9x^3 - 5x^3) + 2x^2 - 5x + (4 - 4 + 7x) (grouping like terms)
= 4x^3 + 2x^2 + 2x (combining like terms)
Therefore, the simplified expression is 4x^3 + 2x^2 + 2x.
We cannot factor this expression further as there are no common factors between the terms.
1) Remove parentheses.
\(9x^{3}+ 2x^{2} -5x+4-5x^{3} +7x-4\)
2) Collect like terms.
\((9x^{3}-5x^{3})+2x^{2} +(-5x+7x)+(4-4)\)
3) Simplify.
\(4x^{3}+2x^{2}+2x\)
--------------------------(DONE)---------------------------------