What is the slope of a line perpendicular to the line y=8x+1?
A. -8
B. 8
C.-1/8
Answers
Answer:
-1/8
Step-by-step explanation:
The sign and number is opposite.
Related Questions
Solve for x. I NEED HELP ASAP!

Answers
Answer:
x = 105
Step-by-step explanation:
The sum of the interior angles of a polygon is
sum = 180° (n - 2) ← n is the number of sides
Here n = 7, thus
sum = 180° × 5 = 900°
Sum the interior angles and equate to 900
x + 102 + 165 + 123 + x + 11 + 128 + 161 = 900, that is
2x + 690 = 900 ( subtract 690 from both sides )
2x = 210 ( divide both sides by 2 )
x = 105
Which statement is correct?
N
H
#
w
T
А.
ATNW - AHCL
В.
ANWT ACHL
C
ANWT 2 ALCH
D
AWTNAHCL

Answers
Answer:
b
Step-by-step explanation:
n hc l
a n w t
yan lng po Ang Alam k
someone help it’s urgent! I’ll brainlist you.

Answers
Answer:
Constant: -17
Coefficient: 7
Number of terms: 3
Step-by-step explanation:
Constant: -17
-> This is the number that doesn't change. No matter what m or p is, -17 will be -17
Coefficient: 7
-> The coefficient is the number next to the variable. In this case, the number "with" (being multiplied by) p is 7
Number of terms: 3
-> There are three terms. A term includes positive/negative, number, variables, etc.
-> The terms are:
[] \(9m^{4}\)
[] \(7p\)
[] \(-17\)
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly.
- Heather
Point M is the midpoint of AB. Find BM.

Answers
since we know that M is the midpoint of the AB segment, that simply means that the two halves it makes are congruent, namely AM = BM.
\(\stackrel{AM}{4x+13}~~ = ~~\stackrel{BM}{3x+17}\implies x+13=17\implies x=4~\hfill \stackrel{3(4)~~ + ~~17}{BM=29}\)
The required length of the side BM is 29.
What is algebra?Algebra is a study of mathematical expressions, in which numbers and quantities are represented in formulas and equations by letters and other universal symbols.
In the given question,
Point M is the midpoint of line AB.
AM = 4x + 13,
and BM = 3x + 17
To find the length of MB, use midpoint property.
Since, Point M is the midpoint of AB,
Therefore, AM = MB
4x + 13 = 3x + 17
4x - 3x = 17 - 13
x = 4
The length of MB = 3x + 17 = 3 × 4 + 17 = 12 + 17 = 29.
The length of MB, where M is midpoint of AB, is 29.
To know more about Algebra on:
https://brainly.com/question/24875240
#SPJ2
Which equation has the same solution as x2 + 16x – 11 = 4?
Answers
Answer:
x^2 + 16x - 15 = 0.
Step-by-step explanation:
x^2 + 16x – 11 = 4 Subtract 4 from both sides:
x^2 + 16x - 15 = 0 is one equation with the same roots.
Also any equation which is a multiple of the above will have the same roots. For example if we multiply by 3:
3x^2 + 48x - 45 = 0.
What is -5/12 + 2/3 please I don’t understand
Answers
Step-by-step explanation:
please mark me as brainlest
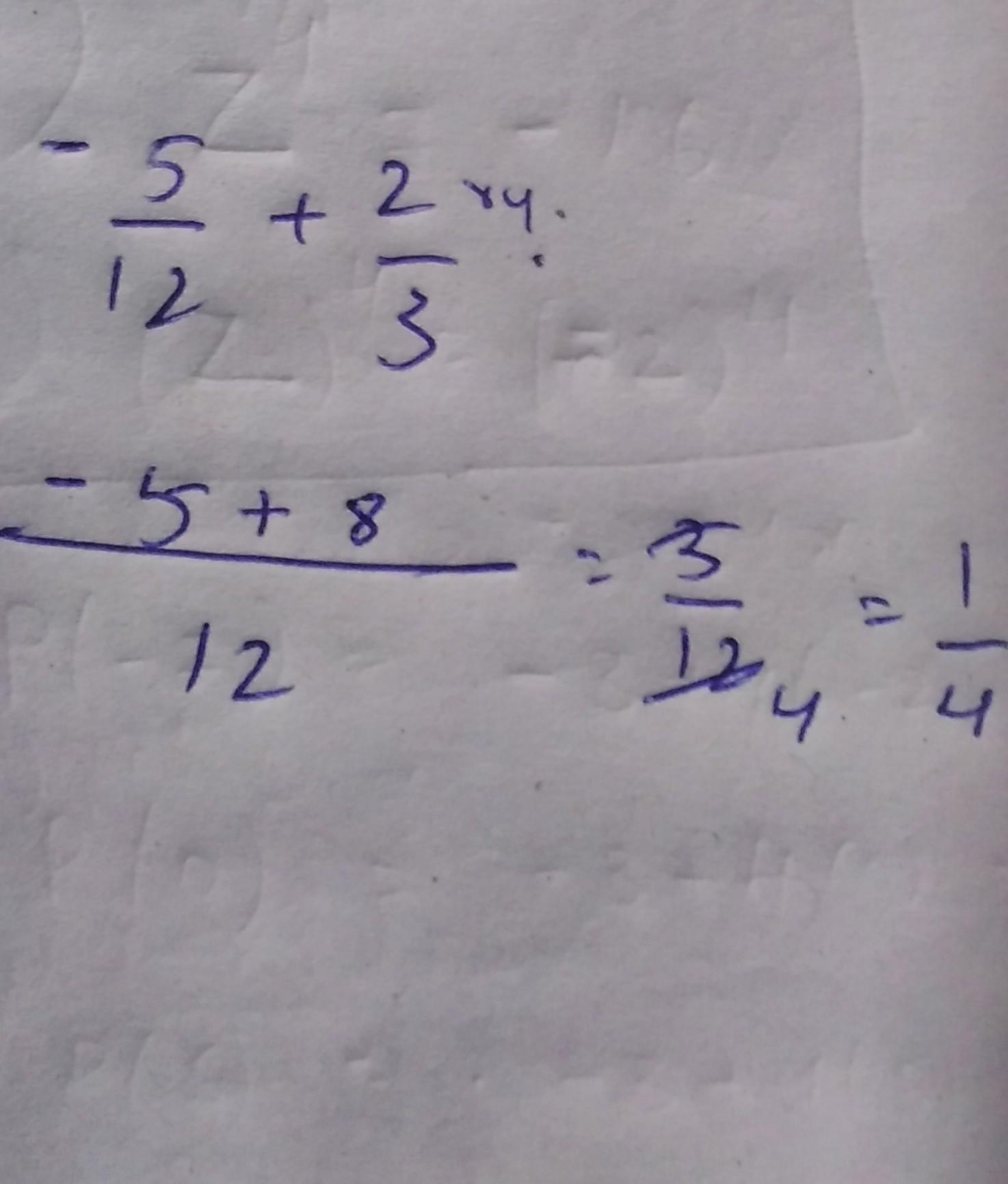
4 = (x+1)^2 what are the solutions to the equation?
(A) x=1 + square root of 2
(B) x= -1 + square root of 2
(C) x= 1 + 2
(D) x= -1+2
Answers
Option C
The solution of equation x^2+3x+4=0 is x= -3+- square root of -7/ 2
Solution: Need to identify correct option for solution of the equation x^2 + 3x + 4 = 0.
Given equation is quadratic equation. We can find solution of this equation using quadratic formula.
According to quadratic formula for general equation solution of the equation is given by
The given equation is So in our case, a = 1, b = 3 and c = 4
On applying quadratic formula we get
As i is square root of -1,
Hence correct option is C that is roots of quadratic equation
Step-by-step explanation: Tell me if i'm wrong
A firm knows its marginal cost of production for a product is MC = 3x + 20 and that marginal revenue for the product is MR = 34 - 4x where x stands for the number of goods produced and sold. What is the optimal level of production for this product (the number of goods that should be produced and sold in order to maximize the profit achieved.) 3 2 14 15
Answers
To find the optimal level of production for this product, we need to set the marginal cost equal to the marginal revenue and solve for x. So, 3x + 20 = 34 - 4x. 7x = 14 x = 2. Therefore, the optimal level of production for this product is 2 goods.
To find the optimal level of production for this product, you should set the marginal cost (MC) equal to the marginal revenue (MR), since the profit is maximized when these two values are equal.
MC = MR
3x + 20 = 34 - 4x
Now, solve for x:
3x + 4x = 34 - 20
7x = 14
x = 2
So, the optimal level of production for this product is 2 goods. This is the number of goods that should be produced and sold in order to maximize the profit achieved.
Learn more about marginal cost here:
brainly.com/question/8993267
#SPJ11
Find the radius of a circle if a 28 foot chord is 6 feet from the center of the circle. (Must be
perpendicular. ) Find the exact value and then round to the nearest hundredth.
Answers
Check the picture below.

Choose the system of equations which matches the following graph.
A. 3x-6y=12
9x-18y=36
B. 3x+6y=12
9x+18y=36
Answers
The system of equations that matches the given graph is:
A. 3x - 6y = 12
9x - 18y = 36
To determine which system of equations matches a given graph, we need to analyze the slope and intercepts of the lines in the graph.
Looking at the options provided:
A. 3x - 6y = 12
9x - 18y = 36
B. 3x + 6y = 12
9x + 18y = 36
Let's analyze the equations in each option:
For option A:
The first equation, 3x - 6y = 12, can be rearranged to slope-intercept form: y = (1/2)x - 2.
The second equation, 9x - 18y = 36, can be simplified to 3x - 6y = 12, which is the same as the first equation.
In option A, both equations represent the same line, as they are equivalent. Therefore, option A does not match the given graph.
For option B:
The first equation, 3x + 6y = 12, can be rearranged to slope-intercept form: y = (-1/2)x + 2.
The second equation, 9x + 18y = 36, can be simplified to 3x + 6y = 12, which is the same as the first equation.
In option B, both equations also represent the same line, as they are equivalent. Therefore, option B does not match the given graph.
for such more question on system of equations
https://brainly.com/question/4262258
#SPJ8
How do I find the X and Y for this equation using elimination method?
6x+6y=54
2x - 6y= 2
Answers
Answer:
X=7 Y=2
I will lead you through it and show you how you can find x through eliminating y, and finding y through eliminating x! So, both ways! :)
Step-by-step explanation:
When looking to use the elimination method, either all x OR y coefficients must be equal before finding one or another. That might sound a little confusing so let me explain!
Finding x by eliminating y: (they already set it up for us, this way!)
6x+6y=54 6y and -6y will cancel each other out!
2x - 6y= 2
6x=54 Add both lines!
2x=2
8x=56 Now, divide 8 on both sides to find x!
x=7 The product is x equals 7! Plug into a line to find y!
6(7)+6y=54
42+6y=54 Subtract both sides by 42
6y=12 Divide both sides by 6
y=2
So, X=7 and Y=2 ! To check that this is true, plug both variables into one line!
2(7)-6(2)=2
14-12=2
2=2 2 equals 2, so this is true! Lets check the other line to make
sure!
6(7)+6(2)=54
42+12=54
54=54 Yes, this is also true! That means we found the true value of the variables. :)
Finding y by eliminating x: Now, how do we find X and Y using the elimination method if the terms are not equal? We will continue to use this problem since it meets the standards of unequal terms! However, we will find y by eliminating x!
We must get the x terms to be equal to they can cancel each other out! So, we will multiply a line by a certain variable until it matches the x term on the other line. We will multiply line 2 until it matches line 1's x term, but make sure the signs (positive/negative) are opposite so they cancel out! In other problems, one line's term may not be able to be multiplied until it reaches its term since it is not a factor of it! So, both lines would be multiplied b a specific number until they have a common multiple! Confusing? Just focus on the underlined portion of this paragraph as that is what you will need for this question. Lets work hard now! :)
6x+6y=54 Multiply line 2 by -3 so the x term will be cancel out line 1's x!
2x - 6y= 2
6x+6y=54
(2x - 6y= 2) -3 Yes, all of it!
6x+6y=54
-6x+18y=-6 Add both lines
24y=48 Divide 24 by both sides!
y=2 y is equivalent to 2! Plug value into a line!
6x+6(2)=54
6x+12=54 Subtract 12 on both sides!
6x=42 Divide 6 on both sides.
x=7 X is equal to 7!
So, X=7 and Y=2 , just like we found and even checked before! I hope this helped. Elimination method is my favorite method and overall favorite lesson in Algebra, for me, since it is pretty easy once you get a hang of it! Goodluck all! :)
The book fair sold 60% of the books
donated to the book fair. They sold
72 books. How many books were
donated in all?
Answers
Answer:
120 Books
Step-by-step explanation:
60% of 120 is 72
What does congruent mean in 6th grade math
Answers
Congruent means equals to
꒰Answer꒱
꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒷꒦
In geometry, two figures/objects are congruent if they have the same shape and size
꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒷꒦
I hope this helps you!! ‘٩꒰。•◡•。꒱۶’
꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒦꒷꒷꒦꒷꒦꒷꒷꒦
- Cherry *・.。
find the angles of a cyclic quadrilateral ABCD in Angle A = (4x+20 )^0 , Angle B = (3x+5 )^0 , Angle C =(4y)^0 , Angle D = (7y-5)^0
Answers
Answer:
<A = 120degrees
<B = 80degrees
<C = 60degrees
<D = 100degrees
Step-by-step explanation:
For a cyclic quadrilateral, the sum of the adjacent angle of the quadrilateral are equal, hence;
<A + <C = 180
<B + <D = 180
Substitute the given values
4x+20+4y = 180
4x+4y =1 60
x + y = 40 ...1
Similarly;
3x+5+7y - 5 = 180
3x+7y = 180 ....2
Solving simultaneously
x + y = 40 ...1 .....* 3
3x+7y = 180 ....2 ...... *1
__________
3x + 3y = 120 ...1 .
3x+7y = 180 ....2
Subtract
3y - 7y = 120 - 180
-4y = -60
y = 15
Since x+y = 40
x + 15 = 40
x = 40 - 15
x = 25
<A = 4x+20
<A = 4(25)+20
<A = 120degrees
<C = 180 - <A
<C = 180 - 120
<C = 60degrees
<B = 3x+5
<B = 3(25)+5
<B = 80degrees
<D = 180 - <B
<D = 180 - 80
<D = 100degrees
Suppose that e and f are two events and that p(e and f)=0.1 and p(e)=0.2. what is p(f|e)?
Answers
The Probability of P(F/E) is 0.5 .
Baye's Theorem helps in finding the conditional probability probability of an event A given that event B has already occurred.
For Example : The probability of event A given that event B has already occurred is denoted by P(A/B) and is calculated by
\(P(A/B)=\frac{P(A.and.B) }{P(B)}\)
It is given in the question that
P(E and F)=0.1 and
P(E)=0.2
Using Baye's Theorem ,we get
\(P(F/E)=\frac{P(F .and .E)}{P(E)}\)
Substituting the values ,we get
\(P(F/E)=\frac{0.1}{0.2}\\ \\ =\frac{1}{2} \\ \\ =0.5\)
Therefore , the probability of P(F/E) is 0.5 .
Learn more about Probability here https://brainly.com/question/17764757
#SPJ4
Help needed ASAP will give BRAINLIEST and 5 stars

Answers
Answer:
1. Dwell.
Step-by-step explanation:
It's the most fitting option.
In the tournament described in Exercise 11 of Section 2.4, a top player is defined to be one who either beats every other player or beats someone who beats the other player. Use the WOP to show that in every such tournament with n players n∈ N, there is at least one top player.
Answers
Using the Well-Ordering Principle (WOP), it can be proven that in every tournament with n players (where n is a natural number), there is at least one top player, defined as someone who either beats every other player or beats someone who beats the other player.
We will prove this statement by contradiction. Assume that there exists a tournament with n players where there is no top player. This means that for each player, there exists either another player who beats them or a chain of players such that each player beats the next one. Now, consider the set S of all players in this tournament. Since S is a non-empty set of natural numbers, it has a least element, let's say k.
Now, player k either beats every other player in the tournament, making them a top player, or there exists a player, let's say player m, who beats player k. In the latter case, we have a chain of players: k, m, p_1, p_2, ..., p_t, where p_1 beats p_2, p_2 beats p_3, and so on until p_t.
However, this contradicts the assumption that there is no top player, as either player k beats every other player (if m does not exist), or player m beats someone who beats the other player (if m exists). Hence, by contradiction, we have shown that in every tournament with n players, there is at least one top player.
Learn more about non-empty set here:
https://brainly.com/question/1581607
#SPJ11
The demand function for a manufacturer's product is p=f(q)=−0.17q+255, where p is the price (in dollars) per unit when q units are demanded (per day). Find the level of production that maximizes the manufacturer's total revenue and determine this revenue. What quantity will maximize the revenue? q= units.
Answers
Given function f(q)=−0.17q+255 is a demand function, which relates price with quantity demanded.
The revenue of a manufacturer can be calculated as total revenue = price × quantity;
which can be expressed as R(q)= q*p=q*(−0.17q+255)=−0.17q²+255q.
To maximize the revenue, we need to take the derivative of the revenue function R(q) with respect to q and set it equal to zero.
Hence, R'(q) = -0.34q + 255 = 0 Or, 0.34q = 255q = 750
Now, the quantity of the manufacturer that will maximize the revenue is 750 units.
Now, to determine the maximum revenue, substitute this value of q in the revenue function.
Hence, R(q) = -0.17q² + 255q R(750) = -0.17(750)² + 255(750) = 106875 units.
Therefore, the maximum revenue is 106875 units when 750 units are produced.
Learn more about maximization: https://brainly.com/question/25120629
#SPJ11
Anyone know? I don’t really get it..

Answers
Answer:
D is the correct ans
Step-by-step explanation:
Because
In a random sample of 200 school district residents, 94 stated they are in favor of starting the school day 15 minutes later each day. Calculate a 90% confidence interval for the true proportion of district residents who are in favor of starting the day later
Answers
The 90% confidence interval for the proportion of district residents in favor of starting the school day 15 minutes later is (0.392, 0.548). The true proportion is estimated to lie within this interval with 90% confidence.
To calculate the 90% confidence interval for the true proportion of district residents who are in favor of starting the school day 15 minutes later, we can use the following formula:
CI = p ± z*(√(p*(1-p)/n))
where:
CI: confidence interval
p: proportion of residents in favor of starting the day later
z: z- score based on the confidence level (90% in this case)
n: sample size
First, we need to calculate the sample proportion:
p = 94/200 = 0.47
Next, we need to find the z- score corresponding to the 90% confidence level. Since we want a two-tailed test, we need to find the z- score that cuts off 5% of the area in each tail of the standard normal distribution. Using a z-table, we find that the z- score is 1.645.
Substituting the values into the formula, we get:
CI = 0.47 ± 1.645*(√(0.47*(1-0.47)/200))
Simplifying this expression gives:
CI = 0.47 ± 0.078
Therefore, the 90% confidence interval for the true proportion of district residents who are in favor of starting the school day 15 minutes later is (0.392, 0.548). We can be 90% confident that the true proportion lies within this interval.
Learn more about the confidence interval here: brainly.com/question/24131141
#SPJ4
the accompanying dataset provides data on monthly unemployment rates for a certain region over four years. compare​ 3- and​ 12-month moving average forecasts using the mad criterion. which of the two models yields better​ results? explain.
Answers
To compare the 3-month and 12-month moving average forecasts using the mean absolute deviation (MAD) criterion, we need to calculate the MAD for each model and then compare them. The MAD is a measure of the average magnitude of the forecast errors, and a lower MAD indicates a better forecast.
To calculate the MAD for the 3-month moving average model, we need to first calculate the forecasted values for each month by taking the average of the unemployment rates for the previous 3 months. For example, the forecasted value for April 2018 would be the average of the unemployment rates for January, February, and March 2018. We then calculate the absolute deviation between the forecasted value and the actual value for each month, and take the average of those deviations to get the MAD for the 3-month moving average model.
We can repeat this process for the 12-month moving average model, but instead of taking the average of the previous 3 months, we take the average of the previous 12 months.
Once we have calculated the MAD for both models, we can compare them to determine which model yields better results. Generally, a lower MAD indicates a better forecast. However, it is important to note that the MAD criterion only considers the magnitude of the forecast errors and does not take into account the direction of the errors (i.e., overestimation versus underestimation).
Learn more about MAD,
https://brainly.com/question/29111637
#SPJ4
Full Question ;
The accompanying dataset provides data on monthly unemployment rates for a certain region over four years. Compare 3- and 12-month moving average forecasts using the MAD criterion. Which of the two models yields better results? Explain. Click the icon to view the unemployment rate data. Find the MAD for the 3-month moving average forecast. MAD = (Type an integer or decimal rounded to three decimal places as needed.) A1 fx Year D E F G H I 1 2 3 1 с Rate(%) 7.8 8.3 8.5 8.9 9.4 9.6 9.4 9.5 9.7 9.9 9.8 10.1 9.9 9.7 9.8 9.91 9.7 9.4 9.6 9.4 9.3 9.5 9.9 9.5 9.2 9.1 8.9 A B Year Month 2013 Jan 2013 Feb 2013 Mar 2013 Apr 2013 May 2013 Jun 2013 Jul 2013 Aug 2013 Sep 2013 Oct 2013 Nov 2013 Dec 2014 Jan 2014 Feb 2014 Mar 2014 Apr 2014 May 2014 Jun 2014 Jul 2014 Aug 2014 Sep 2014 Oct 2014 Nov 2014 Dec 2015 Jan 2015 Feb 2015 Mar 2015 Apr 2015 May 2015 Jun 2015 Jul 2015 Aug 2015 Sep 2015 Oct 5 7 3 ) 1 2 3 1 5 7 9.1 ) 9. 1 2 3 1 5 7 ) 9.1 8.9 8.9 8.9 8.9 8.7 8.4 8.3 8.3 8.4 8.1 8.1 8.4 8.2 8.3 7.7 7.9 7.9 7.8 1 2 2015 Dec 2016 Jan 2016 Feb 2016 Mar 2016 Apr 2016 May 2016 Jun 2016 Jul 2016 Aug 2016 Sep 2016 Oct 2016 Nov 2016 Dec 3 1 5 3 2 2
A farmer plants corn in 1/4 of his field.He plants white corn 3/5 of the corn section of his field.This situation is show in the model. What fraction of the whole field with white corn?
Answers
Answer:
The white corn section covers \(\frac{3}{20}\) of the whole field.
Step-by-step explanation:
The statement indicates that section of the white corn is a portion within the corn section of the field. The statement can be interpreted as a multiplication of rational numbers. That is to say:
\(x = \frac{1}{4} \times \frac{3}{5}\)
\(x = \frac{1 \times 3}{4 \times 5}\)
\(x = \frac{3}{20}\)
The white corn section covers \(\frac{3}{20}\) of the whole field.
Prove that the illumination at a point 0.5 m away from a lamp is
40 m/m2 if the illumination from the same source, 1 m away is 10
m/m2 .
Answers
To prove the relationship between the illumination at two different distances from a lamp, we can use the inverse square law of light propagation. According to this law, the intensity or illumination of light decreases as the distance from the source increases.
The inverse square law states that the intensity of light is inversely proportional to the square of the distance from the source. Mathematically, it can be expressed as:
I1 / I2 = (D2 / D1)^2 where I1 and I2 are the illuminations at distances D1 and D2, respectively. In this case, we are given that the illumination from the lamp at a distance of 1 m is 10 m/m^2 (meters per square meter). Let's assume that the illumination at a distance of 0.5 m is I2.
Using the inverse square law, we can write the equation as:
10 / I2 = (1 / 0.5)^2
Simplifying the equation, we have:
10 / I2 = 4
Cross-multiplying, we get:
I2 = 10 / 4 = 2.5 m/m^2
Therefore, we have proven that the illumination at a point 0.5 m away from the lamp is 2.5 m/m^2, not 40 m/m^2 as stated in the question. It seems there may be an error or inconsistency in the given values.
Learn more about inverse square law here: brainly.com/question/15481424
#SPJ11
1. Does the system of linear equations shown below have a solution? Explain.

Answers
Answer:
hb Step-by-step explanation:
Find the shortest distance from the point (2,0,-3) to the plane x+y+z=1
Answers
Shortest distance from the point (2, 0, -3) to the plane x + y + z = 1 is √3 units.
How to find the shortest distance from a point to a plane?To find the shortest distance between a point and a plane, we can use the formula:
distance = |ax + by + cz + d| / √(a² + b² + c²)
where a, b, and c are the coefficients of the plane's equation, d is the constant term, and (x, y, z) is the coordinates of the point.
In this case, the plane is x + y + z = 1, so a = 1, b = 1, c = 1, and d = -1. The point is (2, 0, -3), so x = 2, y = 0, and z = -3. Plugging in these values, we get:
distance = |1(2) + 1(0) + 1(-3) - 1| / √(1² + 1² + 1²)
= 3 / √3
= √3
Therefore, the shortest distance from the point (2, 0, -3) to the plane x + y + z = 1 is √3 units.
Learn more about constant term.
brainly.com/question/26099230
#SPJ11
\(3 + 3 + 3 = \)
\(5 + 5 + 5 + 5 = \)
\(5 + 5 + 3 = \)
\(3 + 3 + 3 + 5 = \)
\(5 + 5 + 5 = \)
\(5 + 5 + 3 - 3 = \)
\(5 + 5 + 3 + 3 + 3 = \)
NO FILES PLEASE
Answers
Answer:
\(3 + 3 + 3 =9 \)
\(5 + 5 + 5 + 5 =20 \)
\(5 + 5 + 3 =13 \)
\(3 + 3 + 3 + 5 = 14\)
\(5 + 5 + 5 =15 \)=15
\(5 + 5 + 3 - 3 =10 \)
\(5 + 5 + 3 + 3 + 3 =19 \)
Answer:
Step-by-step explanation:
3+3+3=9
5+5+5+5=20
3+3+3+5=14
5+5+5=15
5+5+3-3=10
5+5+3+3+3=19
6 chairs cost £84 in total.
How much does 1 chair cost?
Give your answer in pounds (£).
Answers
Answer: £14
Step-by-step explanation:
Divide the pounds from the chairs, in this case £84 / 6 is £14. So each chair costs £14.
can someone help me solve for y and x and find out the angles of all the angles visable

Answers
Answer:
x = 10 , y = 15
Step-by-step explanation:
8x - 10 and 7x are alternate angles and are congruent , then
8x - 10 = 7x ( subtract 7x from both sides )
x - 10 = 0 ( add 10 to both sides )
x = 10
Then
8x - 10 = 8(10) - 10 = 80 - 10 = 70
6y + 20 and 8x - 10 are same- side interior angles and sum to 180°, that is
6y + 20 + 70 = 180
6y + 90 = 180 ( subtract 90 from both sides )
6y = 90 ( divide both sides by 6 )
y = 15
g(t)=−9t−4g, left parenthesis, t, right parenthesis, equals, minus, 9, t, minus, 4
g\Big(g(g, left parenthesis
\Big)=23)=23
Answers
The resulting expression if the value of t is 23 is g(23) = -4g - 207
Function and valuesA function is an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Given the function below;
g(t)=−9t−4g
We are to determine the value of g(23). Substitute t = 23;
g(t)=−9t−4g
g(23) = -9(23) - 4g
g(23) = -207 - 4g
g(23) = -4g - 207
Hence the resulting expression if the value of t is 23 is g(23) = -4g - 207
Learn more on function and value here: https://brainly.com/question/2284360
#SPJ1
(4x10^3) (7x10^4) perform the indicated computation
Answers
Answer:
28x^11000
Step-by-step explanation:
4x103(7x104)
Simplifies to:
28x11000