What is the product of −2 1/4 and 2 1/2?
Enter your answer as a mixed number, in simplified form, in the box.

Answers
Answer:
-5 5/8
Step-by-step explanation:
-2 1/4 * 2 1/2
~Turn into improper fractions
-9/4 * 5/2
~Multiply both numerators and denominators
-45/8
~Turn into a mixed number
-5 5/8
Best of Luck!
Related Questions
what is C in the triangle
C=
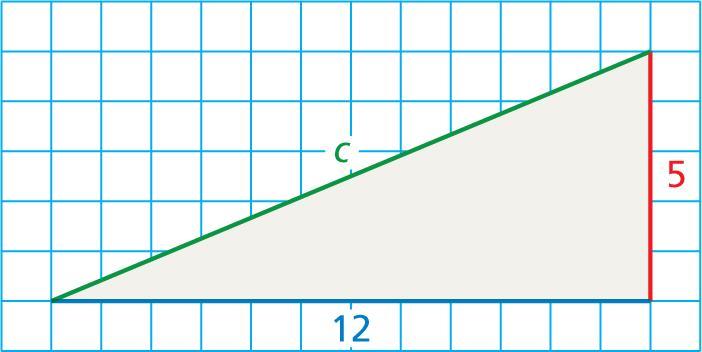
Answers
Answer:
C = 13
Step-by-step explanation:
\(A^{2}\) + \(B^{2}\) = \(C^{2}\)
\(5^{2}\) + \(12^{2}\) = 169
\(\sqrt{169}\) = 13
Answer:
C = 13
Step-by-step explanation:
Use the following formula to answer this question.
C = square root a^2+b^2
Rewrite the formula using the information you already know.
C = square root 5^2 + 12^2
C = 13
I hope this helped to answer your question.
please explain how to use cancellation method with examples. I'm really confused...
Answers
Answer:
Cancellation it enables us to eliminate or get rid of one of the variables, so we can solve a more simplified equation.
Some textbooks refer to the elimination method as the addition method or the method of linear combination.
This is because we are going to combine two equations with addition!
Step 1
First, we align each equation so that like variables are organized into columns.
Step 2
Second, we eliminate a variable.
If the coefficients of one variable are opposites, you add the equations to eliminate a variable, and then solve.
If the coefficients are not opposites, then we multiply one or both equations by a number to create opposite coefficients, and then add the equations to eliminate a variable and solve.
Step 3
Thirdly, we substitute this value back into one of the original equations and solve for the other variable.
Example of how to apply the elimination method for solving systems of equations is attached.

A box contains 11 transistors, 4 of which are defective. If 4 are selected at random, find the probability of the statements below a. All are defective b. None are defective
Answers
The probability that none of the 4 selected transistors are defective is approximately 0.2884.
a. To find the probability that all 4 transistors selected are defective, we can use the formula for probability of multiple independent events:
P(all defective) = P(defective) * P(defective) * P(defective) * P(defective)
Since there are 4 defective transistors out of 11 in total, the probability of selecting a defective transistor on the first draw is 4/11. Since the draws are independent, the probability of selecting a defective transistor on the second draw is also 4/11, and so on. Therefore:
P(all defective) = (4/11) * (4/11) * (4/11) * (4/11) ≈ 0.0026
So the probability that all 4 selected transistors are defective is approximately 0.0026.
b. To find the probability that none of the 4 selected transistors are defective, we can again use the formula for probability of multiple independent events:
P(none defective) = P(not defective) * P(not defective) * P(not defective) * P(not defective)
Since there are 4 defective transistors out of 11 in total, the probability of selecting a non-defective transistor on the first draw is 7/11. Since the draws are independent, the probability of selecting a non-defective transistor on the second draw is also 7/11, and so on. Therefore:
P(none defective) = (7/11) * (7/11) * (7/11) * (7/11) ≈ 0.2884
So the probability that none of the 4 selected transistors are defective is approximately 0.2884.
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
Can u please answer this question in the picture below or above I guess

Answers
Answer: B. 72ᴼ alternate exterior angles theorem
Step-by-step explanation:
Alternate exterior angles because they’re angles on the outside of the transversal.
Alternate exterior angles are also congruent to each other, so that’s why 2 is congruent to 72ᴼ
!!!!Help Plz!!!!
What is the measure of GHI in the figure below?

Answers
Answer:
<GHI =
Step-by-step explanation:
135°
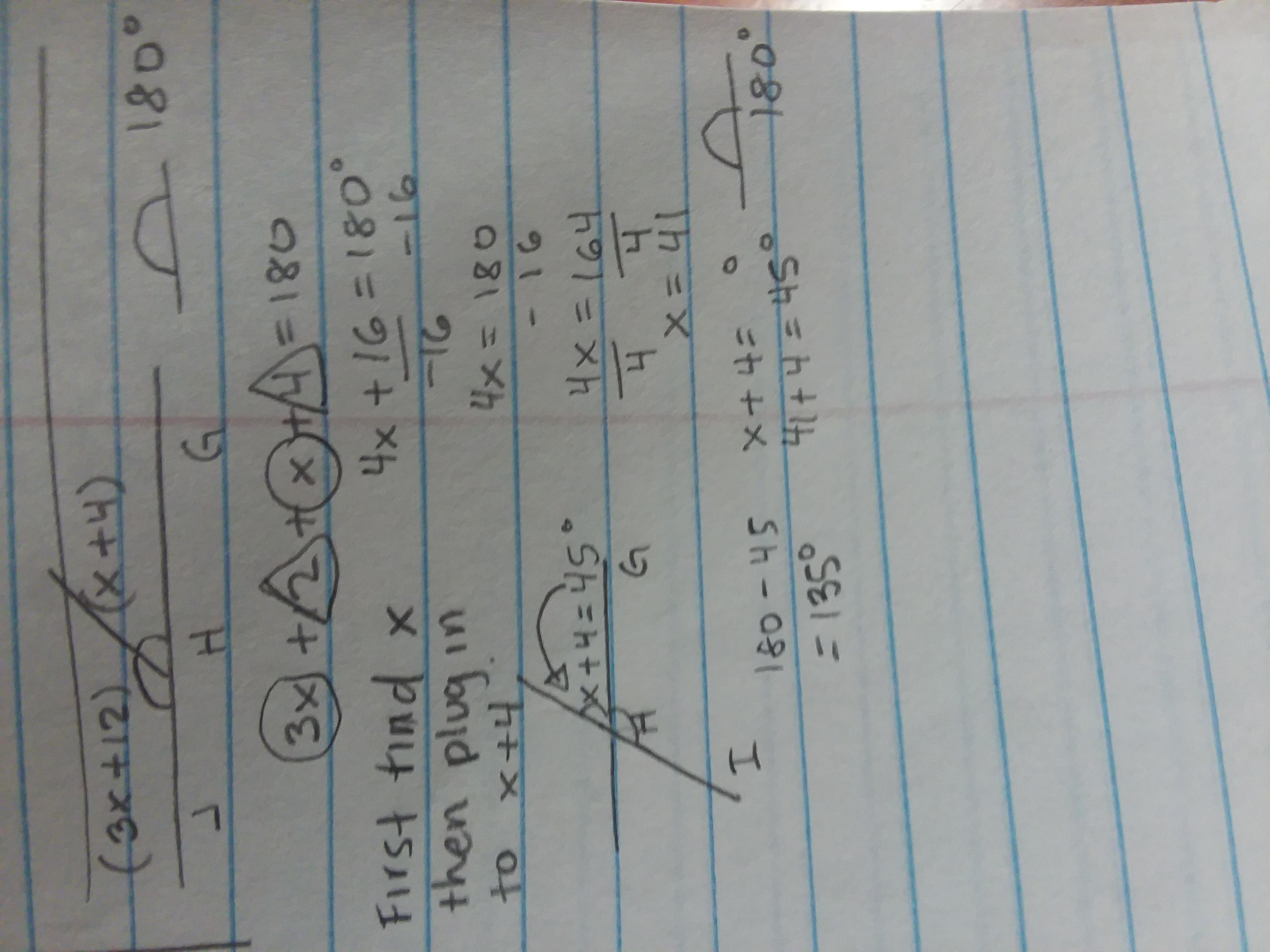
A copy machine can print 360 copies every 4 minutes. How many copies can it print in 12 minutes?
Answers
Answer:
1080
Step-by-step explanation: multiply by 3!!
Answer:
in 4 minutes is 1440 and in 12 minutes is 4320
Step-by-step explanation:
because you have multiply the 4 and the 12 by 360
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I, find the value of tan(A−B).
Answers
If cosA = 24/25 tanB = 4/3 and angles A and B are in Quadrant I. The value of tan(A-B) is -23/33.
What is the value of tan(A-B)?We can start by using the identity: tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
From the given information, we have:
cos A = 24/25, which means sin A = sqrt(1 - cos^2 A) = 7/25 (since A is in Quadrant I)
tan B = 4/3, which means sin B = 4/sqrt(4^2 + 3^2) = 4/5 and cos B = 3/sqrt(4^2 + 3^2) = 3/5
Now, we can use the definitions of sine and cosine to find tan A:
tan A = sin A / cos A = (7/25)/(24/25) = 7/24
Substituting the values we have found into the formula for tan(A - B), we get:
tan(A - B) = (tan A - tan B)/(1 + tan A tan B)
= [(7/24) - (4/3)]/[1 + (7/24)(4/3)]
= (-13/72)/(25/72)
= -13/25
Therefore, tan(A - B) = -13/25.
Learn more about tan(A - B) here:https://brainly.com/question/24305408
#SPJ1
Solve each system by substitution.y - 4x = 3 2x - 3y = 211. Rewrite the first equation in terms of . y=2. Substitute the value of into the second equation. 2x - 3 = 213. Solve for X .4. Substitute the value of in one of the original equations. Solve for y .5. Write your answer as an ordered pair (x,y) .Solution: ( , )

Answers
We have to solve this system by substitution.
This method let us define a varaible in function of the other (or others, if they are more than two) and then replace it in the other equations by this relation.
The system is:
\(\begin{gathered} y-4x=3 \\ 2x-3y=21 \end{gathered}\)1. From the first equation, we can easily define y in function as x:
\(\begin{gathered} y-4x=3 \\ y=4x+3 \end{gathered}\)2. Now, we substitute y in the second equation:
\(\begin{gathered} 2x-3y=21 \\ 2x-3(4x+3)=21 \end{gathered}\)3. We got an equation that is expressed only in function of x, so we can solve it as:
\(\begin{gathered} 2x-3(4x+3)=21 \\ 2x-3\cdot4x-3\cdot3=21 \\ 2x-12x-9=21 \\ -10x=21+9 \\ -10x=30 \\ x=\frac{30}{-10} \\ x=-3 \end{gathered}\)4. If we replace x in the equation for y, we get:
\(\begin{gathered} y=4x+3 \\ y=4(-3)+3 \\ y=-12+3 \\ y=-9 \end{gathered}\)5. Then, we can write the answer a s a pair (x,y) = (-3,-9)
The expression 2.5a+2b gives the cost (in dollars) for a DVDs and b CDs at a moving sale. a. The cost for 1 DVD is $ and the cost for 1 CD is $ . b. The total cost for 4 DVDs and 4 CDs is $ . Question 2 c. Is $20 enough to buy 6 DVDs and 3 CDs?
Answers
Answer/Step-by-step Explanation:
Given:
a = no. of DVDs
b = no. of CDs
Total cost ($) for DVDs and CDs = \( 2.5a + 2b \)
a. The cost for 1 DVD = 2.5(a) = 2.5(1) = $2.5
The cost for 1 CD = 2(b) = 2(1) = $2
b. Total cost for 4 DVDs and 4 CDs:
Substitute a = 4, and b = 4 into the equation.
\( 2.5(4) + 2(4) \)
\( 10 + 8 = 18 \)
Total cost for 4 DVDs and 4 CDs = $18
c. To find out if $20 would be enough to buy 6 DVDs and 3 CDs, substitute a = 6, and b = 3 into the equation. Solve for the total cost to see if it equals $20 or is less than $20. If it's greater than $20, then it won't be enough.
\( 2.5(6) + 2(3) \)
\( 15 + 6 = 21 \)
6 DVDs and 3 CDs cost more than $20, therefore, $20 is not enough.
Determine whether the integral is convergent or divergent. [infinity] 137xe^-x^2 dx
integral.gif
−[infinity]
O convergentO divergent
If it is convergent, evaluate it. (If the quantity diverges, enter DIVERGES.)
Answers
The value of the integral is \((137/2) \sqrt(\pi).\)
How to find the value of the integral?To determine the convergence of the integral, we can use the limit comparison test. We compare the given integral with the integral of a known function that has the same behavior for large values of x.
Let's choose the function \(f(x) = e^(^-^x^2).\)
Then we have:
∫ from -∞ to ∞ 137x \(e^(^-^x^2)\)dx ≤ ∫ from -∞ to ∞ \(e^-^x^2 dx\)
To evaluate the integral on the right-hand side, we can use the fact that:
∫ from -∞ to ∞ \(e^-^x^2 dx\) = \(\sqrt(\pi)\)
Therefore, we have:
∫ from -∞ to ∞ 137x \(e^-^x^2 dx\) ≤ \(\sqrt(\pi)\)
Since \(\sqrt(\pi)\) is a finite constant, the given integral is convergent.
To evaluate the integral, we can use integration by parts.
Let u = x and dv = 137 \(e^-^x^2 dx\), so that du/dx = 1 and v = (-137/2) \(e^-^x^2 dx\).
Then we have:
∫ from -∞ to ∞ 137x \(e^-^x^2 dx\) = [-137x \(e^-^x^2^/^2 dx\)] from -∞ to ∞ + ∫ from -∞ to ∞ (137/2) \(e^-^x^2 dx\)
The first term evaluates to zero because \(e^-^x^2\) goes to zero faster than x as x approaches infinity. Therefore, we have:
∫ from -∞ to ∞ 137x \(e^-^x^2dx\) = (137/2)∫ from -∞ to ∞ \(e^-^x^2 dx\)= \((137/2) \sqrt(\pi)\)
Therefore, the value of the integral is \((137/2) \sqrt(\pi).\)
Learn more about integral
brainly.com/question/30900582
#SPJ11
4x-1+3x-1+7x=180 I can’t believe I can’t get my answer
Answers
The value x of given linear equation in one variable is \(13\)
To solve for x in the equation \(4x-1 +3x -1 +7x = 180\), we first need to combine the like terms on the left side:
\(4x-1 +3x -1 +7x = 180\)
Next, we can isolate the variable term by adding \(2\) to both sides:
\(14x -2 +2 = 180+2\\14x = 182\)
Finally, we can solve for x by dividing both sides by \(14\):
\(x = \frac{182}{14}\)
This can be simplified by dividing both the numerator and denominator by their greatest common factor, which is \(14\):
\(x = 13\)
Therefore, the value of \(x\) that satisfies the equation \(4x-1 +3x -1 +7x = 180\) is \(x = 13\)
To Know more about linear equation in one variable visit:
https://brainly.com/question/11897796
#SPJ1
what happens to the expected value of M a, sample size increases? a. It decreases 10, b. t also increases. e. It stays constant. d· The expected value does not change in a predictable manner when sample size increases.
Answers
The expected value of M does not change in a predictable manner when sample size increases; it can increase, decrease, or stay the same.
The expected value of M, or the mean of a sample, is determined by the values of the individual elements that comprise it. As such, when the sample size increases, the expected value of M could increase, decrease, or remain constant, depending on the particular values of the individual elements in the sample. This is because the expected value of M is the average of the individual elements and the contribution of each element to the average depends on its value and the number of elements in the sample. Therefore, the expected value of M does not change in a predictable manner when sample size increases. Depending on the individual elements in the sample, the expected value of M could be higher, lower, or constant.
Learn more about expected value here
https://brainly.com/question/18523098
#SPJ4
True or False. A confidence interval for proportions is used to estimate the population proportion not the sample proportion True False
Answers
The statement A confidence interval for proportions is used to estimate the population proportion not the sample proportion is true.
A confidence interval for proportions is a statistical tool used to estimate the range of values within which the population proportion is likely to lie. It is calculated based on the sample proportion, sample size, and a specified level of confidence.
The sample proportion is only used as a point estimate of the population proportion, but the confidence interval takes into account the variability of the sample proportion and provides a range of values that are likely to include the population proportion with a certain level of confidence.
for such more question on confidence interval
https://brainly.com/question/14771284
#SPJ11
ggjfhghfhtdhdhdttjtjfj
Answers
Tamela compared the rates of three cable companies.
TV Watchers—$63.00 for 140 channels
Tel-EVision—$53.75 for 125 channels
Channels Galore—$41.80 for 110 channels
Which cable company has the best rate of price per channel?
Channels Galore has the best rate for price per channel.
Tel-EVision has the best rate for price per channel.
TV Watchers has the best rate for price per channel.
All of the companies have the same rate.
Answers
Answer:y = 4x-5.
Step-by-step explanation:
The ratio of c:d is 1:3. The ratio of d:e is 2:3. What is the ratio of c:d:e?
Answers
The ratio of c:d:e is 1:3:2.
How The answer was obtainedTo find the ratio, you can multiply the first ratio by the second ratio: 1 * 2 = 2 and 3 * 3 = 9, so the ratio becomes 2:9:6, which can be simplified to 1:3:2.
A ratio is a comparison between two values. To calculate a ratio, divide the first value by the second value. For example, if you have three apples and seven bananas, the ratio of apples to bananas would be 3/7.
You can also simplify a ratio by dividing both values by their greatest common divisor. For example, if the ratio of apples to bananas is 6/14, you could simplify it to 3/7.
It's also possible to express a ratio as a fraction, decimal, or percentage. To convert a ratio to a fraction, simply divide the two values. To convert a ratio to a decimal, divide the numerator by the denominator. To convert a ratio to a percentage, multiply the ratio by 100.
Learn more on calculations for ratio here https://brainly.com/question/2328454
#SPJ1
Use the discriminant to determine how many and what kind of solutions the quadratic equation 3x^2 -4x=-2 has.
Answers
Find the value of x. Write your answer in simplest form.

Answers
See the workup in photo below.
Find the area and circumference of a circle with the
radius of 8.5 cm.
Answers
Answer:
Area: 226.98
Circumference: 53.41
Step-by-step explanation:
Answer:
Area = 72.25π ≈226.98 cm
Circumference = 17π ≈ 53.41 cm
Step-by-step explanation:
Area formula for a circle = πr²
Circumference formula = 2πr
r = 8.5cm
Find a vector equation and parametric equations for the line. (Use the parameter \( t \).) the line through the point \( (5,3,3) \) and parallel to the vector \( 3 \mathbf{i}-\mathbf{j}+7 \mathbf{k} \
Answers
The Parametric equations for the line (5+ 3t, 3 - t, 3 + 7t).
The equation given by
r(t) = (5i + 3j + 3k) -t(3i - j +7k)
= (5 + 3t)i (3 - t)j +(3 + 7t)
The vector equation is:
[x(t), y(t), z(t)] = (5+ 3t, 3 - t, 3 + 7t)
Therefore, the Parametric equations for the line (5+ 3t, 3 - t, 3 + 7t).
Learn more about Parametric equations here:
brainly.com/question/29168942
#SPJ4
Complete Question:
Find a vector equation and parametric equations for the line. (Use the parameter \( t \).) the line through the point \( (5,3,3) \) and parallel to the vector \(\( 3 \mathbf{i}-\mathbf{j}+7 \mathbf{k}\)
You must decide whether to buy new machinery to produce product X or to modify existing machinery. You believe the probability of a prosperous economy next year is 0.7. Prepare a decision tree and use it to calculate the expected value of the buy new option. The payoff table is provided below (+ for profits and - for losses).
When entering the answer, do not use the $ symbol. Do not enter the thousand separator. Enter up to 2 decimal places after the decimal point. For example, $6,525.35 must be entered as 6525.35
N1: Prosperity ($) N2: Recession ($)
A1 (Buy New) $1,035,332 $-150,000
A2(Modify) $823,625 $293,648
Answers
The expected value of the "Buy New" option is 724732.60.
Decision Tree:
To solve the given problem, the first step is to create a decision tree. The decision tree for the given problem is shown below:
Expected Value Calculation: The expected value of the "Buy New" option can be calculated using the following formula:
Expected Value = (Prob. of Prosperity * Payoff for Prosperity) + (Prob. of Recession * Payoff for Recession)
Substituting the given values in the above formula, we get:
Expected Value for "Buy New" = (0.7 * 1,035,332) + (0.3 * -150,000)Expected Value for "Buy New" = 724,732.60
Therefore, the expected value of the "Buy New" option is 724,732.60.
Conclusion:
To conclude, the decision tree is an effective tool used in decision making, especially when the consequences of different decisions are unclear. It helps individuals understand the costs and benefits of different choices and decide the best possible action based on their preferences and probabilities.
The expected value of the "Buy New" option is 724,732.60.
For more questions on expected value
https://brainly.com/question/14723169
#SPJ8
15 points to Answer this!! Really need help this Important!!

Answers
Answer:
where is your 15 points
Step-by-step explanation:
this answer is 8points
ase logo ko pagal mat banaya karo
Write the equation of the line in fully simplified slope-intercept form

Answers
Answer:
Take 2 points through which the line is passing.
Let it be (0, -3) and (1, 2)
\(slope ,m = \frac{y_{2} -y_{1} }{x_{2} -x_{1} } = \frac{2--3}{1-0} = 2+3 = 5\)
\(equation \ of \ the \ line = (y - y_2) = m(x - x_2)\\\)
\((y - 2) = 5( x - 1)\\y - 2 = 5x - 5 \\y = 5x - 5 + 2\\y = 5x -3\)
guys Im getting a tattoo I'm 13 tho..but should I get butterflies or hearts? let me know assasp
Answers
solve for X
2x(x-1/2)=0
Answers
Answer:
x=0, 1/2
Step-by-step explanation:
Answer:
x=0, x=1/2
Step-by-step explanation:
2x(x-1/2)=0
Use the zero factor Principle
x=0 or x-1/2=0
Solve x-1/2=0;
Add 1/2 to both sides;
x-1/2+1/2=0+1/2
Simplify;
x=1/2
The solutions to the quadratic equations are;
x=0, x=1/2
Answered by NONE other than the ONE & ONLY #QUEEN herself aka #DRIPPQUEENMO!!!
HOPE THIS HELPED!!!
Which of these numbers equals -6*(-1/2)?
A. -3
B. -2
C. 2
D. 3
Answers
Answer:
D option
Step-by-step explanation:
Refer to attachment.
Hope it helps.

Answer: D) 3
Step-by-step explanation:
Have a good day:)
find the critical value(s) and rejection region(s) for the type of z-test with level of significance . include a graph with your answer. right-tailed test, a=0.03.
Answers
Answer:
c
Step-by-step explanation:
The red line represents the critical value, and the shaded region on the right-hand side of the red line represents the rejection region. If the calculated test statistic is greater than the critical value of z, which is 1.88 in this case, we will reject the null hypothesis.
The critical value(s) and rejection region(s) for the type of z-test with a level of significance a = 0.03 and a right-tailed test are as follows :Step 1: Determine the critical value of zThe critical value is calculated by using the normal distribution table and the level of significance. A right-tailed test will have a critical value of zα. For a level of significance of 0.03, we will look for the z-value that corresponds to 0.03 in the normal distribution table.Critical value for a = 0.03 is z = 1.88 (approx).Step 2: Determine the Rejection Region The rejection region for a right-tailed test is defined as any z-value that is greater than the critical value. That is, if the test statistic is greater than 1.88, we reject the null hypothesis at the 0.03 level of significance, and if it is less than or equal to 1.88, we fail to reject the null hypothesis.Therefore, the rejection region for a right-tailed test with a level of significance of 0.03 is as follows:Rejection Region: Z > 1.88 OR Z ≤ -1.88Graph: The graph for the given values will be as follows:The red line represents the critical value, and the shaded region on the right-hand side of the red line represents the rejection region. If the calculated test statistic is greater than the critical value of z, which is 1.88 in this case, we will reject the null hypothesis.
To know more about critical value Visit:
https://brainly.com/question/32607910
#SPJ11
Simplify.
2(m + 11)
2m + 11
2m + 22
24m
22m
Answers
Answer:
b 2m + 22
Step-by-step explanation:
m times 2 is 2m and 11 times 2 is 22
Answer:
2m + 22
Step-by-step explanation:
Step 1: Write expression
2(m + 11)
Step 2: Distribute (Distributive Property)
2m + 22
We simply distribute 2 to each term in the parenthesis.
what is the solution to 2x+10=28
Answers
Given the equation:
\(2x+10=28\)to solve for x, first we have to move the constant 10 to the right side of the equation. When we do this, we have to change its sign to a negative sign:
\(\begin{gathered} 2x+10=28 \\ \Rightarrow2x=28-10=18 \\ 2x=18 \end{gathered}\)Now we can divide both sides of the equation by 2 to get the following:
\(\begin{gathered} \frac{1}{2}(2x=18)\Rightarrow\frac{2}{2}x=\frac{18}{2}=9 \\ \Rightarrow x=9 \end{gathered}\)therefore, x = 9
hello, whats up? i have got a question what is the answer for this equation will mark brainlest n-8= -32 and 2-4n =66
Answers
Answer:
see explanation
Step-by-step explanation:
n - 8 = - 32 ( add 8 to both sides )
n = - 24
---------------------
2 - 4n = 66 ( subtract 2 from both sides )
- 4n = 64 ( divide both sides by - 4 )
n = - 16