What is the least common denominator of 2/3 and 17/20
Answers
Answer:
60 is the least common denominator.
2/3 = 40/60
17/20 = 51/60
Solution
Rewriting input as fractions:
2/3, 17/20
For the denominators (3, 20) the least common multiple (LCM) is 60.
Therefore, the least common denominator (LCD) is 60.
Calculations to rewrite the original inputs as equivalent fractions with the LCD:
2/3 = 2/3 × 20/20 = 40/60
17/20 = 17/20 × 3/3 = 51/60
Related Questions
On which triangle can the law of cosines be used to find the length of an unknown side?
Law of cosines: a2 = b2 + c2 – 2bccos(A)
Triangle Q R S is shown. The length of Q R is s, the length of R S is q, and the length of Q S is 12. Angle R Q S is 36 degrees, angle Q S R is 57 degrees, and angle S R Q is 87 degrees.
Triangle Q R S is shown. The length of Q R is s, the length of R S is 7, and the length of Q S is 12. Angle R S Q is 57 degrees.
Triangle Q R S is shown. The length of Q R is s, the length of R S is 7, and the length of Q S is b. Angle R S Q is 57 degrees and angle S Q R is 36 degrees.
Triangle Q R S is shown. The length of Q R is s, the length of R S is q, and the length of Q S is 12. Angle R Q S is 36 degrees and angle Q S R is 57 degrees.
Answers
Answer:
(b) Triangle QRS is shown. The length of QR is s, the length of RS is 7, and the length of QS is 12. Angle RSQ is 57 degrees.
Step-by-step explanation:
The Law of Cosines can be used to find an unknown side when that side is opposite a known angle, and the lengths of the sides of that angle are known. That will be the case when the known sides share a vertex, and the angle at that vertex is known.

Answer: OPTION B
Step-by-step explanation:
rate of change for y=5x+25
Answers
Answer:5
Step-by-step explanation:
rate of change is the same thing as slope (or m)
The required rate of change for the given equation y = 5x + 25 is 5.
Given that,
For the given equation y =5x +25 the rate of change is to be determined.
The slope of the line is the tangent angle made by line with horizontal. i.e. m =tanx where x in degrees.
What is the rate of change?The rate of change is defined as the change in value with the rest of the time is called rate of change.
Here,
The given equation,
y = 5x + 25
Differentiate the above equation with respect to x,
dy/dx = d(5x +25)/dx
dy/dx = 5dx/dx + d25/dx
dy/dx = 5 (since dx/dx =1 and d25/dx = 0)
here dy/dx is the slope of the equation or m or rate of change = 5
Thus, the required rate of change for the given equation y = 5x + 25 is 5.
Learn more about the rate of change here:
https://brainly.com/question/13103052
#SPJ2
Can someone pls help me

Answers
Answer:
6
Step-by-step explanation:
\( {(3 \sqrt{13}) }^{2} - {9}^{2} = {x}^{2} \\ 9(13) - 81 = {x}^{2} \\ 117 - 81 = {x}^{2} \\ 36 = {x}^{2} \\ x = 6
Use Pythagorean theorem
\(\\ \sf\longmapsto P^2=H^2-B^2\)
\(\\ \sf\longmapsto P^2=(3√13)^2-9^2\)
\(\\ \sf\longmapsto P^2=117-81\)
\(\\ \sf\longmapsto P^2=36\)
\(\\ \sf\longmapsto P=6\)
help please??????????????????

Answers
Answer:
-5 and 2
-2 and -1
-3 and 0
There is no shortcut to solving this type of problem. You just have to use trial and error.
:)
Answer:
-2+ (-3)
-5+ 0
-1+ (-2)+ (-2)
Hope this helps!
LMK if it does
x = 1 - y² and x = y² - 1. sketch the region, set-up the integral that Consider the region bounded by would find the area of the region then integrate to find the area.
Note: • You may use the equation function (fx) in the answer window to input your solution and answer, OR
• Take a photo of your handwritten solution and answer then attach as PDF in the answer window.
Answers
The region bounded by the curves x = 1 - y^2 and x = y^2 - 1 is a symmetric region about the y-axis. It is a shape known as a "limaçon" or
"dimpled cardioid."
To find the area of the region, we need to determine the limits of integration and set up the integral accordingly. By solving the equations
x = 1 - y^2
and
x = y^2 - 1
, we can find the points of intersection. The points of intersection are (-1, 0) and (1, 0), which are the limits of integration for the y-values.
To calculate the area, we integrate the difference between the upper curve (1 - y^2) and the lower curve (y^2 - 1) with respect to y, from -1 to 1:
Area =
∫[-1,1] (1 - y^2) - (y^2 - 1) dy
After evaluating the integral, we obtain the area of the region bounded by the given curves.
To learn more about
Area
brainly.com/question/30307509
#SPJ11
In this triangle, what is the value of x?

Answers
Answer: 4.46cm
Step-by-step explanation:
Use [SOH CAH TOA]
We have two sides that are labeled. Use 85cm and x.
Using the angle 63 degrees would mean you are using SOH.
SOH = Opposite/Hypotenuse.
If the above is true, then: Sin63 = x/85
Since we don't know what x is, you want to move 85 to the other side.
85(Sin63) = x
Now, you can find x. Multiply 85 and Sin63. Your answer should be 4.46 (if rounded to 2 decimals).
Find 15% more than rupees 60
Answers
Answer: 60rupees*1.15=69 rupees
Step-by-step explanation: 15% more is 15% + 100% so 15% more of 60 rupees is 60*1.15
SOMEONE PLEASE HELP I NEED THE ANSWER NOW AND RIGHT NOW PLEASEEEEE!!!!!!

Answers
Answer:
B
Step-by-step explanation:
Its easy
please help me!
NO BOTS

Answers
Answer:
16 < 24 < 25
Step-by-step explanation:
√16 = 4
√25 = 5
f(13) = -3x+ 7
What’s the answer?
Answers
Answer:
3.3
Step-by-step explanation:
7-7=0
-3+-7=-10
10 divided by 3 is 3.3
A biologist is studying a group of alligators in a swamp and tagged 4 hatchlings, 5 juveniles, and 6 adults. The biologist estimates that this tagged sample is a reliable reflection of the ratios of hatchlings, juveniles, and adults in the general alligator population for the area. The biologist estimates that the total number of alligators in the area is 120. The most likely number of adults in the total population is ______?
A. 32
B. 48
C. 72
D. 120
AND PLZ NO LINKSSSS
Answers
Answer:
48
Step-by-step explanation: Take the 6 adults and divide it by one of the multiple choice answers to get a ratio. The ratio of 48 / 6 = 8. You can then see if that ratio helps you add up all the alligators to 120.
4 x 8 + 5 x 8 + 6 x 8 = 120
Help <3
also I need help with the unit I don't know what they mean by units

Answers
Answer:
2 floors/second
Step-by-step explanation:
The points on the graph at the ends of the interval of interest are ...
(seconds, floors) = (3, 3) and (5, 7)
The slope of the line between these points is given by the slope formula:
m = (y2 -y1)/(x2 -x1)
where the points are (x1, y1) and (x2, y2). For the points shown above, the slope is ...
m = (7 floors -3 floors)/(5 seconds -3 seconds)
= (4 floors)/(2 seconds) = 4/2 floors/second = 2 floors/second
In your answer form:
A = 2
B = floors
C = second
_____
Additional comment
Any measurement will vary, depending on the units in which the measurement is made. A length, for example, might be 12 inches, or 1 foot. The length numbers 12 or 1 don't mean anything, unless you know the units they are counting.
__
When x- and y-values are pure numbers, their ratio, or the ratio of their changes, is a pure number. It has no units. We do a lot of algebra this way. (This is mainly to get you used to doing the arithmetic without having the confusion of units getting in the way.)
When x- and y-values on a graph are identified as having particular units, the slope of any curve on that graph has units that are the ratio of the y-units to the x-units. (Any area on the graph will be the product of the x-units and the y-units.)
Here, the units of the vertical (y) scale are "floors." The units of the horizontal (x) scale are "seconds". You know this because that is how the graph is labeled. Then the slope of a line on the graph has units of ...
"y-units"/"x-units" = floors/second
The choice of singular or plural for the units depends a little on what makes sense in English. Usually, the denominator unit will be singular. Often, the numerator unit is plural, especially of the value is more than 1.
__
As we show above, you can do the math with the units attached to the numbers. They are treated algebraically as though they are variables. Only numbers with like units can be added or subtracted. (You cannot add (combine) 3 inches and 4 feet for the same reason you cannot add 3x and 4y—they are unlike terms.) You can multiply and divide units as needed. For computing area, we often do something like (3 ft)(4 ft) = 12 ft·ft = 12 ft².
If you make it a practice to consider units along with the numbers, you will find they help you do the correct arithmetic. If you are considering an area computation that does not result in square units, for example, you might need to do a units conversion or reconsider the proposed computation. Using units in computation is especially helpful in physics and chemistry.
find the truth set of each predicate. a. predicate: 6/d is an integer, domain: z b. redicate: 1≤x^2 ≤ 4, domain: Z
Answers
To find the truth set of the predicate "6/d is an integer" over the domain of integers (Z), we need to determine all the values of d for which the statement is true. a) Therefore, the truth set of the predicate is {1, 2, 3, 6}. b) the truth set of the predicate is {1, 2}.
First, we note that 6/d can only be an integer if d is a divisor of 6. The divisors of 6 are 1, 2, 3, and 6.
For d = 1, we have 6/1 = 6, which is an integer. For d = 2, we have 6/2 = 3, which is also an integer. For d = 3, we have 6/3 = 2, which is an integer. For d = 6, we have 6/6 = 1, which is an integer. Therefore, the truth set of the predicate is {1, 2, 3, 6}.
To find the truth set of the predicate "1≤x^2 ≤ 4" over the domain of integers (Z), we need to determine all the values of x for which the statement is true. First, we note that x^2 can only be an integer if x is an integer. The integers between 1 and 4 (inclusive) are 1, 2, 3, and 4.
For x = 1, we have 1^2 = 1, which satisfies the predicate. For x = 2, we have 2^2 = 4, which also satisfies the predicate.
For x = 3, we have 3^2 = 9, which is not less than or equal to 4, so it does not satisfy the predicate. For x = 4, we have 4^2 = 16, which is not less than or equal to 4, so it does not satisfy the predicate.
Therefore, the truth set of the predicate is {1, 2}.
Know more about integer here:
https://brainly.com/question/15276410
#SPJ11
at a certain auto parts manufacturer, the quality control division has determined that one of the machines produces defective parts of the time. if this percentage is correct, what is the probability that, in a random sample of parts produced by this machine, exactly are defective?
Answers
The probability of a random sample of parts produced by this machine being exactly defective = 0.15
Step-by-step explanation:
Let the percentage of defective part be 12%
and the sample be out of 7 , 2 are defective.
P(X=x) = (e-λ λ x)/ x! [ poisson distribution]
Since, 12% defective parts is produced by one of the machines of the time.
μ= (12%×7)= 0.84
the number of defective product =2
Therefore ,
P(X=2) = 0.15
Thus the required probability becomes 0.15
In Statistics, Poisson distribution is one of the important topics. It is used for calculating the possibilities for an event with the average rate of value. Poisson distribution is a discrete probability distribution.
To learn more about Poisson distribution
https://brainly.com/question/24327826
#SPJ4
QUESTION:
Image below
20points!!!

Answers
Answer:
Step-by-step explanation:
X. 2 2 -3
-4 -6 2
There are 150% more MMs in the regular size bag than the fun size. If there are 6 MMs in the fun size bag, how many are there in the regular size bag?
Answers
Answer:
9
Step-by-step explanation:
150% - 1.5
6*1.5 = 9
There are 9 MMs in the regular sized bag.
Answer:
15 MMsStep-by-step explanation:
There are 150% more MMs than 6:
6 + 150% = 6 + 6*1.5 = 6 + 9 = 15If B = [4 -1 2 0] , what is detB⁻¹ ?
Answers
The value of the determinant of the inverse of the matrix \(\(B\)\) \(\(\text{det}(B^{-1})\) is \(\frac{1}{2}\)\).
Given the matrix \(\(B = \begin{bmatrix} 4 & -1 & 2 & 0 \end{bmatrix}\)\), we need to find \(\(\text{det}(B^{-1})\)\) .
First, let's calculate the determinant of the matrix \(\(B\)\), denoted as \(\(\text{det}(B)\)\):
\(\[\text{det}(B) = 4 \cdot (-1 \cdot 0 - 2 \cdot 2) - (-1) \cdot (4 \cdot 0 - 2 \cdot 2) + 2 \cdot (4 \cdot 2 - (-1) \cdot (-1)) \\= 4 \cdot (-4) - (-1) \cdot (-4) + 2 \cdot (8 - 1) \\= -16 + 4 + 14 \\= 2.\]\)
Now, we can find the determinant of the inverse of the matrix \(\(B\)\), denoted as \(\(\text{det}(B^{-1})\)\):
\(\[\text{det}(B^{-1}) = \frac{1}{\text{det}(B)} \\= \frac{1}{2}\]\)
Therefore, \(\(\text{det}(B^{-1}) = \frac{1}{2}\)\).
Learn more about determinants: https://brainly.com/question/16981628
#SPJ11
Ryan is planning to attend a public university after he graduates from high school in 2 years. He is devising a plan to save money each month to help with the expenses of attending the university. The cost of attending the public university for one-year is $24,500. His family has promised to contribute $12,700 each year he is in school. What is the minimum amount of money Ryan must contribute to his savings per month for the next 2 years to have enough money to pay for his first year of tuition?
a
$491.67
b
$459.58
c
$387.51
d
$587.85
Answers
Answer:
A. 491.67
Step-by-step explanation:
please rank brainliest:)
Help me. I'm so stinking confused.

Answers
Answer: There are 7 coffee shops per square mile
Step-by-step explanation:
1,400,000/100,000=14
14x17=238
238/34=7
You are dealt a hand of three cards, one at a time. Find the probability of each of the following. a) The first diamond you get is the third card dealt. b) Your cards are all spades. c) You get no aces. d) You have at least one red card.
Previous question
Answers
a) The probability of the first diamond being the third card dealt is 1/4.
b) The probability of having all spades in the hand is 1/64.
c) The probability of not getting any aces is 48/64.
d) The probability of having at least one red card is 1 - (probability of having no red cards), which is 1 - 1/4 = 3/4.
a) In a standard deck of 52 cards, there are 13 diamonds. Since the first diamond must be the third card dealt, there are 51 remaining cards after the first two cards are dealt. Out of these 51 cards, 12 are diamonds. Therefore, the probability is 12/51, which simplifies to 1/4.
b) There are 13 spades in a deck, so the probability of getting a spade on the first card is 13/52. For the second card, the probability is 12/51, and for the third card, it is 11/50. Since these events are independent, we multiply the probabilities together: (13/52) * (12/51) * (11/50) = 1/64.
c) There are 4 aces in a deck, so the probability of not getting an ace on the first card is 48/52. Similarly, for the second card, it is 47/51, and for the third card, it is 46/50. Multiplying these probabilities gives (48/52) * (47/51) * (46/50) = 48/64.
d) To find the probability of having at least one red card, we can calculate the probability of having no red cards and subtract it from 1. The probability of not getting a red card on the first card is 26/52, and similarly, for the second and third cards, it is (25/51) * (24/50). The probability of having no red cards is (26/52) * (25/51) * (24/50) = 1/4. Therefore, the probability of having at least one red card is 1 - 1/4 = 3/4.
To know more about probability here: brainly.com/question/32004014 #SPJ11
Solve the system of equations. 3 x + 4 y = − 23 x = 3 y + 1 3x+4y=−23 x=3y+1
x=
Answers
Answer:
x=−5
y=−2
Step-by-step explanation:
{3x+4y=-23}{x=3y+1}
x=−5
y=−2
What’s the length of ab
Answers
The line segment /AB/ would have the length of 18
What is the isosceles triangle?A triangle with two equal sides is known as an isosceles triangle. In other words, two of the three sides of an isosceles triangle are congruent. The third side, known as the base, is usually longer than the other two sides.
In an isosceles triangle, the angles opposite the congruent sides are also congruent. These angles are referred to as the base angles, while the angle directly across from the base is referred to as the vertex angle.
We know that the base angles of the isosceles triangle are equal as such the two sides are equal in length thus;
6x = 3x + 9
6x - 3x = 9
3x = 9
x = 3
Thus the length/AB/= 6(3) = 18
Learn more about isosceles triangle:https://brainly.com/question/29774496
#SPJ1

in order to fairly set flat rates for auto mechanics, a shop foreman needs to estimate the average time it takes to replace a fuel pump in a car. how large a sample must he select if he wants to be 99% confident that the true average time is within 15 minutes of the sample average? assume the standard deviation of all times is 30 minutes.
Answers
The value of n is 25 according to standard deviation in the question.
What is standard deviation?
Standard Deviation is a measure that shows what quantity variation (such as unfold, dispersion, spread,) from the mean exists. the quality deviation indicates a “typical” deviation from the mean. it's a well-liked live of variability as a result of it returns to the first units of live of the info set.
Main body:
s = 30 minutes
C.I. = 99%
mean = 15 minutes
z value for 99% = 2.58
mean = z*s/√n
15 = 2.58 * 30 / √n
√n = 5.06
n = 25
Hence the value of n is 25 .
To know more about standard deviation click on the link below
brainly.com/question/475676
#SPJ4
which of the following points is on the unit circle
Answers
The required answer is the all of the given points (A, B, C, and D) are on the unit circle.
The unit circle is a circle with a radius of 1 unit centered at the origin of a coordinate plane. Points on the unit circle can be represented by their coordinates (x, y), where x is the cosine of the angle and y is the sine of the angle.
To determine which of the following points is on the unit circle, we need to check if the coordinates satisfy the equation x^2 + y^2 = 1. If the coordinates satisfy this equation, then the point is on the unit circle.
consider the points given and check if they are on the unit circle:
- Point A: (1, 0)
- Point B: (0, -1)
- Point C: (-√2/2, √2/2)
- Point D: (0, 1)
Checking each point:
- Point A: (1, 0)
- 1^2 + 0^2 = 1 + 0 = 1
- The coordinates satisfy the equation, so point A is on the unit circle.
- Point B: (0, -1)
- 0^2 + (-1)^2 = 0 + 1 = 1
- The coordinates satisfy the equation, so point B is on the unit circle.
- Point C: (-√2/2, √2/2)
- (-√2/2)^2 + (√2/2)^2 = 2/4 + 2/4 = 4/4 = 1
- The coordinates satisfy the equation, so point C is on the unit circle.
- Point D: (0, 1)
- 0^2 + 1^2 = 0 + 1 = 1
- The coordinates satisfy the equation, so point D is on the unit circle.
In conclusion, all of the given points (A, B, C, and D) are on the unit circle because their coordinates satisfy the equation x^2 + y^2 = 1.
To know about unit circle . To click the link.
https://brainly.com/question/11987349
#SPJ11
3.
Find a relationship between x and y so that (x, y) is equidistant from the two points (3,-1)
and (2,5). Show your work.
Answers
Answer:
The answer is 6.082763
Step-by-step explanation:
We use the Distance formula for this problem.
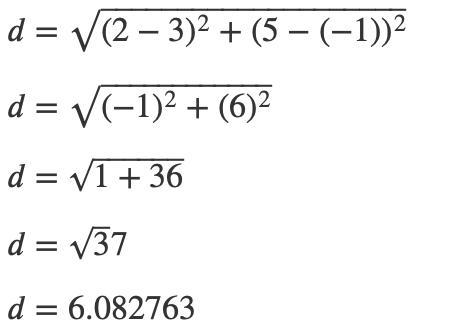
what is the formula for calculating installment
Answers
Answer: The formula is Monthly Payment = P (r(1+r)^n)/((1+r)^n-1)
Step-by-step explanation:
EMI = [P x R x (1+R)^N]/[(1+R)^N-1], where P stands for the loan amount or principal, R is the interest rate per month [if the interest rate per annum is 11%, then the rate of interest will be 11/(12 x 100)], and N is the number of monthly instalments
The forecast for 2019 by the linear regression method is 87.3723 83.7387 89.0824 84.9406
forecasting regression File Edit View Insert Format Tools Data Window T ABC ABC B Calibri 11 fx Σ = A C E ***
Answers
The linear regression method forecasts the values for 2019 as 87.3723, 83.7387, 89.0824, and 84.9406.
To provide a step-by-step explanation of the linear regression method used to forecast the values for 2019:
Linear regression is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. In this case, the dependent variable is the forecasted value for 2019, and the independent variable is time.
The given forecast values, 87.3723, 83.7387, 89.0824, and 84.9406, represent the predicted values for the corresponding time periods.
The linear regression method estimates a straight line that best fits the historical data, allowing for the prediction of future values. In this case, the method estimates the relationship between time and the forecasted values.
By fitting a linear regression model to the historical data, the method calculates the coefficients for the line equation, which represents the trend or pattern observed in the data.
Once the coefficients are determined, the linear regression model can be used to forecast values for future time periods. The model assumes that the relationship between time and the forecasted values will continue to follow the estimated trend.
In this case, the linear regression method predicts the values 87.3723, 83.7387, 89.0824, and 84.9406 for the year 2019 based on the observed trend in the historical data.
It's important to note that without additional context or information about the specific dataset and variables involved, it's difficult to provide a more detailed explanation. The linear regression method relies on the assumption that the relationship between the dependent and independent variables is linear and that there are no other significant factors influencing the forecasted values.
For more questions like Linear regression click the link below:
https://brainly.com/question/32505018
#SPJ11
Joe drives 325 miles to Chicago for a business meeting. If Joe drives at a constant rate of 65 mph, how long will it take to get him to Chicago?
A) 4 hrs.
B)4. 5 hrs.
C)5 hrs.
D)5. 5 hrs.
Answers
It will take Joe 5 hours to reach Chicago.
To calculate the time it will take for Joe to reach Chicago, we can use the formula:
Time = Distance / Rate
Given that Joe drives 325 miles at a constant rate of 65 mph, we can plug these values into the formula:
Time = 325 miles / 65 mph = 5 hours
The correct answer is:
C) 5 hrs.
Know more about Distancehere:
https://brainly.com/question/13034462
#SPJ11
find [t]-1 given that cos sin sin cos and show that [t]21 5[t]t and hence that [t] is an orthogonal matrix.
Answers
TT is equal to T-1, so the given matrix is an orthogonal matrix.
What is an orthogonal matrix?
A matrix is said to be orthogonal if its antipode is also its transpose and if its relationship to the inner product is established. A real square matrix with orthonormal vectors in its columns and rows is known as an orthogonal matrix or orthonormal matrix in direct algebra. Where QT is the transpose of Q and I is the identity matrix is one system to put this into words. However, the matrix is said to be orthogonal, If the transpose of a square matrix with real figures or values is equal to the inverse matrix of the matrix. In other words, an identity matrix will always be affected by the product of a square orthogonal matrix and its transpose.Here, the determinant of T,
|T| = cos²∅ + sin²∅
= 1
Now, its cofactors,
\(T_{11}\) = cos ∅
\(T_{12\) = sin ∅
\(T_{21\)= -sin ∅
\(T_{22\) = cos ∅
Now, the adjoint matrix of cofactors matrix transpose \(T^T\) is equal to \(T^{-1.\)
Hence, the given matrix is an orthogonal matrix.
Learn more about orthogonal matrix here: https://brainly.com/question/13258857
#SPJ4
The point P(6, –1) is translated according to the rule (x, y) → (x – 5, y – 2). What are the coordinates of P'? P'(1, 2) P'(1, 1) P'(1, –3) P'(4, 4)
Answers
Answer:
(1, -3)
Step-by-step explanation:
If the point P(6, –1) is translated according to the rule (x, y) → (x – 5, y – 2).
To get the coordinate of P', we will replace x as 6 and y as -1 in the translation given as shown
Coordinate of P' = (6 -5, -1, -2)
Coordinate of P' = (1, -3)
hence the coordinate of P' is (1, -3)
Answer:
p'(1 -3)
Step-by-step explanation: