What is the equation of the line that passes through (5, -2) and (-3, 4)?
Answers
Answer:
y = (-3/4)x + 7/4
Step-by-step explanation:
Step 1: Define general form of equation of line
An equation of a straight line on two-dimensional plane could be represented in form of: y = Mx + b, with M is slope and b is y-intercept
Step 2: Set up the system to solve for parameters of equation of line
(solve for M and b)
That equation passes 2 points, which are represented in form of (x, y), (5, -2) and (-3, 4).
Substitute these values of x and y into the original equation in step 1:
-2 = 5M + b
4 = -3M + b
Step 3: Solve the system of equations in step 2 for M and b
Subtract 1st equation from 2nd equation:
6 = -8M
=> M = -6/8 = -3/4
Substitute M back into 1st equation:
=> -2 = 5*(-3/4) + b
=> b = -2 + 15/4
=> b = 7/4
=> The equation of the line that passes through (5, -2) and (-3, 4):
y = (-3/4)x + 7/4
Hope this helps!
:)
Answer:
Y= -4/3(x-7/2)
Step-by-step explanation:
So first calculate the difference between them,
changes by 8 x units, and -6 y units.
Then substitute them into y/x to find gradient
-6/8 = -4/3
so now we have a part of the equation:
Y= -4/3(x-a)
substitute Y= -2 and x=5 (from (5,-2))
-2= -4/3(5-a)
-2= -20/3+4a/3
Multiply by 3 on both sides
-6= -20+4a
add 20 on both sides
14=4a
a=7/2
use this as the value of a
Y= -4/3(x-7/2)
Related Questions
How does 5x/4 -2=3x/2-4 simplify to -5/2
Answers
X = 8
Step by step:
Add two to both sides
5x/4 = 3x/2 - 2
Now multiply 4 with both sides
5x = 6x - 8
Take the 5x to the other side
0= 6x -5x -8
0= x - 8
X = 8
Find the magnitude and direction of the vector using the given information. V=<6,7>

Answers
Answer:
The magnitude of the vector is 9.165 and it's direction is 40.6°
Step-by-step explanation:
Vector Quantities:A vector quantity is a quantity that has both size (magnitude) and direction. Examples of vector quantities are force, velocity and impulse.
Magnitude of vector v is given by
|v| = √6²+7²
= √36+49
= √84
= 9.165
Direction of vector v is obtained by:
\( \tan( \theta) = \frac{x}{y} \)
\(\theta = {tan}^{ - 1} ( \frac{6}{7}) \)
\(\theta = {40.6°}\)
Learn more about vector quantities from: https://brainly.in/question/3437975
#SPJ1
Using the Zero Product Property identify the solution set for (x + 3) (x + 8) = 0
a. -3, 8
b. -3, -8
c. 3, 8
d. 3, -8
Answers
solve the equation 2^x + 5 = 3^x + 1 through three iterations of successive approximation. then answer the questions in the table
what is the approximate solution after three iterations?
what is the approximate solution after four iterations?
use graphing technology to find the most accurate answer possible. how does this answer compare with the solution found by four iterations of successive approximation?
Answers
Answer:
1. 29/16=1.8125
2. 59/32=1.84375
3. (word by word so make sure to kinda change it up) Solution found using graphing technology: 1.8453.
1.8453 - 1.84375 = 0.00155. This solution is very close to the solution found using graphing technology.
Step-by-step explanation:
Answer:
Step-by-step explanation:
1. 29/16=1.8125
2. 59/32=1.84375
3. (word by word so make sure to kinda change it up) Solution found using graphing technology: 1.8453.
1.8453 - 1.84375 = 0.00155. This solution is very close to the solution found using graphing technology.

joe is going to travel to dallas. he lives 320 miles away and can average 69 miles per hour. use an equation to represent the distance D from Dallas in terms of h, the number of hours joe has traveled
Answers
Given parameters:
Distance = 320miles
Average speed = 69miles per hour
Unknown;
A motion equation = ?
Given that D should represent Distance
h number of hours traveled by Joe
Speed is a physical quantity defined as the distance divided by time taken.
It is mathematically expressed as;
Speed = \(\frac{Distance}{time taken}\)
Now substitute D for distance and h for the number time;
Speed = \(\frac{D}{h}\)
So distance;
D = Speed x h
For this journey;
D = 69h
The equation is D = 69h
Answer:
The answer is B. D=320-69h
Just took the quiz :)
what is the answer x- 8=-6?
Answers
Step-by-step explanation:
x- 8=-6
x= -6+8
x=2
hope it helps
Answer x=2
Step-by-step explanation:
how would i anwser this? help pls!

Answers
Answer:
Step-by-step explanation:
To get the y values all you need to do is substitute the x value in the equation y=-2/3x+7.
For example:
y=-2/3(-6)=7
-2/3x6=-4
-4+7=3
(-6,3)
You can double check your work by filling the x and y coordinates in the equation and when solved if it it true you know you were correct.
To get the x value, you need to fill in the y in the equation y=-2/3x+7
for example:
5=-2/3x+7
-2=-2/3x
3=x
(3,5)
y=-2/3x+7
y=-2/3(15)+7
y=-10+7
y=-3
(15,-3)
y=-2/3x+7
15=-2/3x+7
8=-2/3x
-12=x
(-12,15)
PLEASE HELP!!! It would be greatly appreciated

Answers
Someone please help me fast! here is screenshot algebra. QUICK PLSSS

Answers
Answer:
\(\displaystyle{f(x)=3^x-5}\)
Step-by-step explanation:
Being translated up-down means that the value exists outside of x. Therefore, we can cancel B and C choice since those are horizontal (left-right) translation.
Our only choice is A and D. However, D is being translated up since it's +5. Thus, the only correct answer that a function is being translated down is:
\(\displaystyle{f(x)=3^x-5}\)
or A choice.
Solve the equation 9 (5 + x) = 15 and 3/7
Write out the steps
Answers
x= 138 (6/7) - 5
x= 143 (6/7)
Jordan is working two summer jobs, making $6 per hour walking dogs and making $15 per hour clearing tables. In a given week, he can work a maximum of 11 total hours and must earn at least $120. If xx represents the number of hours walking dogs and yy represents the number of hours clearing tables, write and solve a system of inequalities graphically and determine one possible solution.
Answers
Answer:
xx=5 and yy=6
Step-by-step explanation:
Hope it helps you
A manufacturer must test that his bolts are 4.00 cm long when they come off the assembly line. He must recalibrate his machines if the bolts are too long or too short. After sampling 121 randomly selected bolts off the assembly line, he calculates the sample mean to be 4.21 cm. He knows that the population standard deviation is 0.83 cm. Assuming a level of significance of 0.02, is there sufficient evidence to show that the manufacturer needs to recalibrate the machines? Step 2 of 3: Compute the value of the test statistic. Round your answer to two decimal places.
Answers
The sample mean of 4.21 cm is significantly different from the specified target mean of 4.00 cm.
Step 1: State the hypotheses.
- Null Hypothesis (H₀): The mean length of the bolts is 4.00 cm (μ = 4.00).
- Alternative Hypothesis (H₁): The mean length of the bolts is not equal to 4.00 cm (μ ≠ 4.00).
Step 2: Compute the value of the test statistic.
To compute the test statistic, we will use the z-test since the population standard deviation (σ) is known, and the sample size (n) is large (n = 121).
The formula for the z-test statistic is:
z = (X- μ) / (σ / √n)
Where:
X is the sample mean (4.21 cm),
μ is the population mean (4.00 cm),
σ is the population standard deviation (0.83 cm), and
n is the sample size (121).
Plugging in the values, we get:
z = (4.21 - 4.00) / (0.83 / √121)
z = 0.21 / (0.83 / 11)
z = 0.21 / 0.0753
z ≈ 2.79 (rounded to two decimal places)
Step 3: Determine the critical value and make a decision.
With a level of significance of 0.02, we perform a two-tailed test. Since we want to determine if the mean length of the bolts is different from 4.00 cm, we will reject the null hypothesis if the test statistic falls in either tail beyond the critical values.
For a significance level of 0.02, the critical value is approximately ±2.58 (obtained from the z-table).
Since the calculated test statistic (2.79) is greater than the critical value (2.58), we reject the null hypothesis.
Conclusion:
Based on the computed test statistic, there is sufficient evidence to show that the manufacturer needs to recalibrate the machines. The sample mean of 4.21 cm is significantly different from the specified target mean of 4.00 cm, indicating that the machine's output is not meeting the desired length. The manufacturer should take action to recalibrate the machines to ensure the bolts meet the required length of 4.00 cm.
for more such question on mean visit
https://brainly.com/question/1136789
#SPJ8
i dont understand how this question works so therefeore i dont know how to do it, can anyone help?
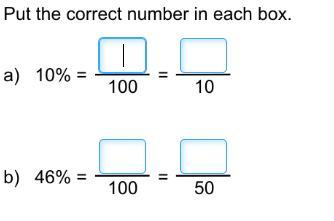
Answers
is simply changing from percentage form to a decimal form usually, but the fractional form works the same. Check the picture below.

Use Pascal's triangle to find the following. Use heads as the x of the first value, reading the triangle from the left to right. write the combination in nCr form and verify with your calculator. the number of ways to get 4 heads and 2 tails tossing a coin 6 times?
10
6
15
20
Answers
According to Pascal's triangle, The number of ways to get 4 heads and 2 tails tossing a coin 6 times is Option C.15
Pascal's Triangle:Pascal's triangle is a mathematical pattern that is named after French mathematician Blaise Pascal.
It is a triangular array of numbers, with the first row having the number 1 and each following row being constructed by adding the two numbers directly above it.
It is used to solve combinatorial problems and to find the binomial coefficients.
For instance, to find the number of ways to get 4 heads and 2 tails while flipping a coin 6 times, Pascal's Triangle is used.
The given question is as follows: Use Pascal's triangle to find the following.
Use heads as the x of the first value, reading the triangle from the left to right. write the combination in nCr form and verify with your calculator.
the number of ways to get 4 heads and 2 tails tossing a coin 6 times.
The solution is as follows: When we flip a coin, we either get a head or a tail.
Therefore, the probability of getting a head is 1/2, while the probability of getting a tail is also 1/2.
We can now use the binomial formula to determine the number of ways to get 4 heads and 2 tails in 6 coin flips: `(6C4)*(1/2)^4*(1/2)^2 = 15`.
This implies that there are 15 ways to get 4 heads and 2 tails when flipping a coin 6 times.
The answer to the given question is C.15.
For more questions on Pascal's triangle
https://brainly.com/question/29174649
#SPJ8
2 starting terms of a diginacci sequence when the 2021st term is 11
Answers
Hello,
In a diginacci sequence, all term is the sum off digits of the 2 terms before.
Answer: 2,3
\(u_{-2}=1\\u_{-1}=1\\u_0=digit(u_{-2})+digit(u_{-1})=1+1=2\\u_1=1+2=3\\u_2=2+3=5\\u_3=3+5=8\\u_4=5+8=13\\u_5=8+1+3=12\\...\\u_{18}=11\\u_{19}=8\\u_{20}=10\\u_{21}=9\\u_{22}=10\\u_{23}=10\\u_{24}=2**********\\u_{25}=3**********\\2020=24*84+4\\u_{2020}=u_{4}=13\\\)
We must begin with 13 , 10
Proof:
Dim a As Long, b As Long, c As Long, nb As Integer
a = 13
b = 10
nb = 1
Print nb, a
While nb < 2021
nb = nb + 1
c = somme&(a, b)
a = b
b = c
' Print nb, a
Wend
Print nb, a
End
Function somme& (a1 As Long, b1 As Long)
Dim strA As String, strB As String, n As Long
strA = LTrim$(Str$(a1))
strB = LTrim$(Str$(b1))
n = 0
For i = 1 To Len(strA)
n = n + Val(Mid$(strA, i, 1))
Next i
For i = 1 To Len(strB)
n = n + Val(Mid$(strB, i, 1))
Next i
somme& = n
End Function
Show the steps needed to Evaluate (2)^-2
Answers
Answer:
\(\dfrac{1}{4}\)
Step-by-step explanation:
Given expression:
\(2^{-2}\)
\(\boxed{\textsf{Exponent rule}: \quad a^{-n}=\dfrac{1}{a^n}}\)
Apply the exponent rule to the given expression:
\(\implies 2^{-2}=\dfrac{1}{2^2}\)
Two squared is the same as multiplying 2 by itself, therefore:
\(\begin{aligned}\implies 2^{-2}&=\dfrac{1}{2^2}\\\\&=\dfrac{1}{2 \times 2}\\\\&=\dfrac{1}{4}\end{aligned}\)
Solution
\(2^{-2}=\dfrac{1}{4}\)
Answer:
1/4
Step-by-step explanation:
Now we have to,
→ find the required value of (2)^-2.
Let's solve the problem,
→ (2)^-2
→ (1/2)² = 1/4
Therefore, the value is 1/4.
For a standard normal distribution, find:
P(z > -1.6)
Express the probability as a decimal rounded to 4 decimal places.
Answers
Answer:
P(z > -1.76) = 1 - P(z < -1.76) = 1 - 0.0392 = 0.960
Using the identity. (a - b) ²= (a² - 2ab + b²), evaluate 699²
Answers
Step-by-step explanation:
hope it helps you.......

\(\\ \sf\longmapsto 699^2\)
\(\\ \sf\longmapsto (700-1)^2\)
\(\\ \sf\longmapsto 700^2-2(700(1)+(1)^2\)
\(\\ \sf\longmapsto 490000-1400+1\)
\(\\ \sf\longmapsto 488600+1\)
\(\\ \sf\longmapsto 488601\)
the phone company charges $33 for having a smartphone plus $9.95 a month for 2gb. IF mark has only $146.43 to spend on a phone, how many months can he have the phone? inequalities
Answers
The number of months Mark can have the phone is given by the equation
A = 11.4 months
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the number of months be represented as = A
Now , the equation is
Now , the total amount with Mark = $ 146.43
The initial amount for the smartphone = $ 33
The amount per month for 2GB is = $ 9.95
So , the amount for A months = $ 9.95 ( A )
So , the equation will be
Initial amount for the smartphone + the amount for A months = total amount with Mark
Substituting the values in the equation , we get
33 + 9.95 ( A ) = 146.43 be equation (1)
On simplifying the equation , we get
Subtracting 33 on both sides of the equation , we get
9.95 ( A ) = 113.43
Divide by 9.95 on both sides of the equation , we get
A = 11.4 months
Therefore , the value of A is 11.4 months
Hence , the number of months is 11.4 months
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
fv=100000, pmt=4000, i/y=5%, n=10, what is pv?
Answers
The Present value is $6,139.132.
We have,
FV=100000, pmt = 4000, I =5%, n=10
So, The present value formula is
PV=FV / (1 + \(i)^n\)
So, PV = 100, 000 / (1+ 5/100\()^{10\\\)
PV = 100,000 / (1+ 0.05\()^{10\\\)
PV = 100, 000/ (1.05\()^{10\\\)
PV = 100,000 / 1.6288946
PV= $6,139.132
Learn more about Future Value here:
https://brainly.com/question/14860893
#SPJ1
Find the Error, a student is simplifying the expression negative cube root 0.125 using rational numbers. The student claims that the expression cannot be simplified because it is not possible to take the square root of a negative number. Find the error made by the student and correct it. Need help ASAP. giving 50 points and brainliest if you solve
Answers
Answer:
Step-by-step explanation:
so the cube root of 0.125 is 0.5
make that a negative so -0.5
=
Homework: HW 4.2
Question 27, 4.4.71
ler
....
If 4 coins can be exchanged for 5.9352 dubloons, how many dubloons can be obtained for 9 coins?
t.c
..
How many dubloons can be obtained for 9 coins?
om
e
(Round to the nearest hundredth.)
...
age...
Answers
Answer:
5.33
Step-by-step explanation:
Is the figure line symmetric?
If yes, how many lines of symmetry does the figure have?
Snow flake
A.
No
B.
Yes; 3 lines of symmetry
C.
Yes; 6 lines of symmetry
D.
Yes; 12 lines of symmetry
Answers
The figure is indeed symmetric and the number of lines of symmetry the snowflake has is C. Yes; 6 lines of symmetry.
How many lines of symmetry does a snowflake have ?Generally a snowflake is hexagonal and has 6-way radial symmetry. Thus, one can rotate it 60 degrees (the sixth of full rotation) and it still appears the same.
So, overall, this means that a snowflake holds 6 lines of symmetry which divide it into two identical halves reflecting each other. Consequently, it can be rotated in 60-degree increments and still holds identicality. Akin to this final property, the snowflake artifact possesses six uniquely divided
Find out more on lines of symmetry at https://brainly.com/question/28709515
#SPJ1
PLEASE HELP DUEEE NOW !!!A diagram of a roundabout that is being designed to improve driver safety on a busy road is shown. The radius of the circular field planned for landscaping is 27.5 feet. What is the approximate distance around the outside of the circular field?
A. 345.4 feet
B. 172.7 feet
C. 86.35 feet
D. 2,323.1 feet

Answers
The approximate distance around the outside of the circular field is the circumference = 172.7 feet and the correct option is B.
How to evaluate for the circumference of a circleTo calculate the circumference of a circle, multiply the diameter of the circle with π (pi). The circumference can also be calculated by multiplying 2×radius with pi (π = 3.14).
We shall derive the approximate distance around the outside of the circular field by calculating for the circumference as follows:
Radius of the circular feild = 27.5
circumference of the circular feild = 2 × 27.5 feet × 3.14
circumference of the circular feild = 55 feet × 3.14
circumference of the circular feild = 172.7 feet.
Therefore, the approximate distance around the outside of the circular field is derived as the circumference which is equal to 172.7 feet.
Know more about circle here: https://brainly.com/question/20489969
#SPJ1
Jug A contains 6/7 as much water as Jug B.Jug C contains 3/5 as much water as Jug A.Find the ratio of the volume of water in Jug B to the volume of water as Jug C.
Answers
The ratio of the volume of water in Jug B to the volume of water in Jug C is 35:18.
Let's assume the volume of water in Jug B is x.
According to the given information, Jug A contains 6/7 as much water as Jug B. Therefore, the volume of water in Jug A can be calculated as (6/7) * x.
Similarly, Jug C contains 3/5 as much water as Jug A. Hence, the volume of water in Jug C can be expressed as (3/5) * [(6/7) * x].
To find the ratio of the volume of water in Jug B to the volume of water in Jug C, we divide the volume of water in Jug B by the volume of water in Jug C:
(x) / [(3/5) * (6/7) * x]
Simplifying the expression, we get:
x / (18/35 * x)
The x values cancel out, leaving us with:
1 / (18/35)
To simplify further, we multiply the numerator and denominator by the reciprocal of the denominator:
1 * (35/18)
The final ratio is:
35/18
For more such questions on ratio
https://brainly.com/question/30370621
#SPJ8
Solve for x.
\(\mathrm{3^{2x}=11}\)
\(\sf[ Round\; to \;two \;decimal \;places\; as\; needed]\)
Answers
Step-by-step explanation:
3^2x = 11
we take the logarithm (to the base of 3) of both sides.
log3(3^2x) = log3(11)
2x = log3(11) = log(11)/log(3)
x = log(11)/log(3) / 2 = log(11)/(2×log(3)) =
= 1.091329169... ≈ 1.09
Answer:
3^2x = 11
we take the logarithm (to the base of 3) of both sides.
log3(3^2x) = log3(11)
2x = log3(11) = log(11)/log(3)
x = log(11)/log(3) / 2 = log(11)/(2×log(3)) =
= 1.091329169... ≈ 1.09
Step-by-step explanation:
Suppose that the radius of a sphere is divided by 9. What happens with the surface area?

Answers
Answer:
Rad/9
Step-by-step explanation:
Here’s is a graph of the function f.
Use the graph to find the following.
If there is more than one answer, separate them with commas

Answers
Answer:
The local minima are 1 and -2
The values at which the function f has a local minimum are -3 and 4
Step-by-step explanation:
Main Concepts:
Brief side-discussion about local vs global minimums
Concept 1. What a Local minimum is
Concept 2. Where a local minimum is at
Brief side-discussion: a Local minimum vs Absolute or Global minimum
A local minimum is the height of any "low" point on a continuous section of the function where all of the points "near" it are higher.
In contrast, an Absolute minimum (sometimes called a "global minimum"), is the lowest height the function ever reaches.
Concept 1. What a Local minimum is
This problem is asking about local minimums, of which there are two:
the height of the point in the trough on the leftthe height of the point in the trough on the right"The Local minimum value" itself IS the height of the point (the "y"-value).
The point on the left has coordinates (-3,1), and the point on the right has coordinates (4,-2).
So, the local minima are 1 and -2
Concept 2. Where a local minimum is at
The minima are different from "The values AT which the function has a local minimum" which is the input (or, "x"-value) that will produce that output when put into the function.
So, the values at which the function f has a local minimum are -3 and 4
For triangle ABC (shown here), the value of angle BCD is equal to 30 degrees. If CD is the height of the triangle and is 12 centimeters, then what is the perimeter of triangle ABC?

Answers
The perimeter of triangle ABC could be either approximately 27.98 cm or approximately 14.66 cm, depending on the length of AB.
What is the perimeter?
The perimeter is a mathematical term that refers to the total distance around the outside of a two-dimensional shape. It is the length of the boundary or the sum of the lengths of all the sides of a closed figure.
Let's call the length of AB x and the length of BC y.
First, we can use the fact that CD is the height of the triangle to find the area of triangle ABC:
Area of triangle ABC = 1/2 * CD * AB
Substituting the given values, we have:
1/2 * 12 * x = 6x
So the area of triangle ABC is 6x square centimeters.
We can also use the fact that angle BCD is 30 degrees to set up a trigonometric equation involving x and y:
tan(30) = x/y
Simplifying, we get:
y = x/tan(30) = x/(1/√(3)) = √(3) * x
Now we can use the formula for the area of a triangle in terms of its sides:
Area of triangle ABC = 1/2 * AB * BC * sin(B)
where B is the angle between sides AB and BC. In this case, we know that angle BCD is 30 degrees, so angle BCA is 60 degrees, and angle ABC is 90 degrees. Therefore, we have:
Area of triangle ABC = 1/2 * x * √3 * x * sin(60)
Simplifying, we get:
Area of triangle ABC = 1/4 * √3 * x²
Since we already found that the area of triangle ABC is 6x square centimeters, we can set these two expressions equal to each other and solve for x:
6x = 1/4 * √(3) * x²
Multiplying both sides by 4/√3, we get:
24/√(3) * x = x²
Simplifying, we get:
x² - 24/√(3) * x = 0
Using the quadratic formula, we get:
x = (24/√(3) ± √((24/√(3))² - 410)) / 2*1
Simplifying, we get:
x = 16√(3) / 3 or x = 8 √(3) / 3
Since we are looking for the perimeter of triangle ABC, we need to find y as well. Using the equation we derived earlier, we have:
y = √(3) * x
Therefore, we have two possible triangles:
Triangle ABC1: AB = 16 √(3) / 3, BC = 16, and AC = 8 √7 / 3
Triangle ABC2: AB = 8 √3 / 3, BC = 8, and AC = 4 √7 / 3
The perimeter of each triangle is the sum of its side lengths. Therefore:
Perimeter of triangle ABC1 = 16 √3/ 3 + 16 + 8 √7 / 3 ≈ 27.98 cm
Perimeter of triangle ABC2 = 8 √3 / 3 + 8 + 4 √7 / 3 ≈ 14.66 cm
hence, the perimeter of triangle ABC could be either approximately 27.98 cm or approximately 14.66 cm, depending on the length of AB.
To learn more about the perimeter visit:
brainly.com/question/397857
#SPJ1
Calculator What is the area of a sector with a central angle of 144° and a radius of 11 cm? Use 3.14 for π and round your final answer to the nearest hundredth. Enter your answer as a decimal in the box. cm² K
Answers
Rounding to the nearest hundredth, the area is approximately 151.976 cm².
The formula for the area of a sector is:
A = (θ/360) x πr²
where θ is the central angle in degrees, r is the radius, and π is pi (3.14).
Plugging in the given values, we get:
A = (144/360) x 3.14 x 11^2
A = 0.4 x 3.14 x 121
A = 151.976
To learn more about the area;
https://brainly.com/question/27683633
#SPJ1