Answers
Answer:
4 dollars per week
Step-by-step explanation:
Related Questions
I’m circle Y, what is m

Answers
In circle Y, the measure of m∠SZT is equal to: B. 94°.
What is a chord of circle?In Mathematics, a chord of circle can be defined as a line segment that typically join any two (2) points of a circle.
Generally speaking, the inscribed angle of a circle is equal to half of the central angle of a circle. Mathematically, this is given by this mathematical expression:
m∠STR = 1/2(SYR)
m∠STR = 1/2(50)
m∠STR = 50°.
m∠TSU = 1/2(TYU)
m∠TSU = 1/2(72)
m∠TSU = 36°.
For m∠SZT, we have the following:
m∠SZT = 180° - (m∠STR + m∠TSU)
m∠SZT = 180° - (50 + 36)
m∠SZT = 180° - 84°
m∠SZT = 94°
Read more on intersecting chords here: https://brainly.com/question/27251228
#SPJ1
If the first urn has 8 blue balls and 2 red balls, the second urn has 8 blue balls and 2 red balls, and the third urn has 7 blue balls and 3 red balls. What is the probability of drawing 1 blue ball?
Your answer:
a) 0
b) 8/10
c) 988/1000
d) 52/1000
e) 448/100
f) 960/100
Answers
The probability of drawing 1 blue ball from the first, second, and third urns is calculated using the formula: probability of drawing 1 blue ball from the first urn = 4/5, probability of drawing 1 blue ball from the second urn = 4/5, and probability of drawing 1 blue ball from the third urn = 7/10. The weighted average of these probabilities is then calculated, resulting in the correct option of 52/1000.
If the first urn has 8 blue balls and 2 red balls, the second urn has 8 blue balls and 2 red balls, and the third urn has 7 blue balls and 3 red balls, the probability of drawing 1 blue ball is given as follows:
Probability of drawing 1 blue ball from the first urn = (number of blue balls in the first urn)/(total number of balls in the first urn)
= 8/(8 + 2)
= 4/5
Probability of drawing 1 blue ball from the second urn = (number of blue balls in the second urn)/(total number of balls in the second urn) = 8/(8 + 2)
= 4/5
Probability of drawing 1 blue ball from the third urn = (number of blue balls in the third urn)/(total number of balls in the third urn)
= 7/(7 + 3)
= 7/10
Therefore, the probability of drawing 1 blue ball from the three urns is the weighted average of the probability of drawing 1 blue ball from each urn. So, we multiply each probability by the proportion of balls in each urn and add them up.
So, the probability of drawing 1 blue ball from the three urns is given by:
(4/5)*(1/3) + (4/5)*(1/3) + (7/10)*(1/3)
= 52/150
= 26/75
So, the correct option is d) 52/1000.The probability of drawing 1 blue ball from the three urns is 52/1000.
To know more about probability Visit:
https://brainly.com/question/31828911
#SPJ11
The Mean, Median and only Mode of 5 numbers, 15, 12, 14, 19 and x, are all equal. Find the value of x.
Answers
If the Mean, Median and only Mode of 5 numbers, 15, 12, 14, 19, and x, are all equal, the value of x must be 15.
What is the mean, median, and mode?The mean of a data set refers to the average value, which is obtained as the quotient of the total value divided by the number of items in the data set.
The median is the central (middle) value when the values of the data set are arranged in ascending or descending order.
The mode is the value that occurs most in the data set.
15, 12, 14, 19, and x
The total value = 75 (15 + 12 + 14 + 19 + x), where x = 15
Mean = 15 (75 ÷ 5)
Median = 15 (12, 14, 15, 15, 19)
Mode = 15 (15, 15, occurring more than the other numbers).
Learn more about the mean, median, and mode at https://brainly.com/question/14532771.
#SPJ1
If f (x)=3^5-x + 6, what is the value of f (5), to the nearest tenth?
Answers
Answer:
240
Step-by-step explanation:
3^5 - 5 + 6
243 - 5 = 238+6= 244
240?
help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
Find integer matrices A,B not multiples of each other such that Nul(A)=Nul(B) and Col(A)=Col(B).
Answers
The matrices A and B that were defined are the integer matrices:
A = [1 0 0; 0 1 0]
B = [1 1 0; 0 0 0]
Both A and B are integer matrices, and they have the same null space and column space but are not multiples of each other. Therefore, they satisfy the requirements " Integer matrices A,B not multiples of each other such that Nul(A)=Nul(B) and Col(A)=Col(B)."
Let A and B be 3x3 matrices given by:
A = [1 0 0; 0 1 0]
B = [1 1 0; 0 0 0]
We can see that A and B have the same null space and column space, but they are not multiples of each other. To show that A and B have the same null space, we need to find the null space of both matrices.
For A, we need to solve the equation Ax = 0:
[1 0 0; 0 1 0] [x1; x2; x3] = [0; 0]
This Equations has the unique solution x = [0; 0; 0], so null space of A is the trivial subspace {0}.
For B, first solve the equation Bx = 0:
[1 1 0; 0 0 0] [x1; x2; x3] = [0; 0]
This equations has the general solution x = [-x2; x2; x3], where x2 and x3 are arbitrary integers, so null space of B is the subspace spanned by the vector [-1; 1; 0].
Show that A and B have the same column space, we have to show the columns of A and B span the same subspace. The columns of A are [1; 0] and [0; 1], which span the entire 2-dimensional space. The columns of B are [1; 0] and [1; 0], which span the 1-dimensional subspace { [x; x] : x is an integer }. But, the column space of A is also the subspace { [x; y] : x and y are integers }, which is the same as the column space of B.
Therefore, A and B have the same column space.
Since A and B have the same null space and column space but are not multiples of each other, they satisfy the conditions " integer matrices A,B not multiples of each other such that Nul(A)=Nul(B) and Col(A)=Col(B)."
To know more about Integer Matrices:
https://brainly.com/question/29348107
#SPJ4
Function p represents the number of people in the library on a Monday as a function of hours since the library opened.
Here is the graph of function p

Answers
Answer:
C (3rd choice)
Step-by-step explanation:
Domain (x-values):
We can see that there is a max number of 14 hours and a min. of 0 hours. This means that the domain is [0, 14]. Note that the domain would be in brackets (as opposed to parentheses) because the values are included in the data set. Since time works on a continuum, it can be reasonably concluded that all values should be included (e.g., 1.5 hours exists). Therefore, we would state that all numbers from 0 to 14 are valid in the domain.
Range (y-values):
We can see that there is a max of 85 people and a min. of 0 people. This means that the range is [0, 85]. Again, since the values 0 and 85 are both included in the data, the range is notated in brackets. Be mindful that there is no such thing as half person, so the range must only include whole numbers. That means this chart acts as a step-function.
Helpppp
Evan spent 20 hours doing homework last week. This week he spent 25 hours doing homework. He says that he spent 125% more time doing homework this week. Is he correct? Show your work to justify your decision.
Answers
Answer: Evan is incorrect
Step-by-step explanation:
20/20 - 25 x 100 =
5/20 x 100/1 =
500/20
500/20 = 20%
Evan would only be correct is he doubled the 20 hours to make it 40 hours
Hope this helps✌
he charactertistic polynomial of the matrix C=[-3, 0, 6; -6, 0, 12; -3, 0, 6]
is p(λ)= −λ2(λ−3).
The matrix has two distinct eigenvalues, λ1<λ2:
λ1=________ has an algebraic multiplicity(AM)=____ the dimension of the corresponding eigenspace (GM) is___
λ2=_____has an algebraic multiplicity(AM)=____ the dimension of the corresponding eigenspace (GM) is___
Is the matrix C diagonalizable? (enter YES or NO)
Answers
The matrix has two distinct eigenvalues, λ1<λ2:
λ1= 0 has an algebraic multiplicity(AM)= 2 the dimension of the corresponding eigenspace (GM) is 1
λ2= 3 has an algebraic multiplicity(AM)= 1 the dimension of the corresponding eigenspace (GM) is 1
Matrix C is NOT diagonalizable.
The characteristic polynomial of the matrix C is given as p(λ) = -λ^2(λ-3). To find the eigenvalues, we set p(λ) = 0.
-λ^2(λ-3) = 0
This equation has two distinct eigenvalues, λ1 and λ2:
λ1 = 0, which has an algebraic multiplicity (AM) of 2 (since the exponent of λ^2 is 2). To find the dimension of the corresponding eigenspace (GM), we solve the system (C - λ1I)x = 0, which is already in the form of matrix C. Since there is only one independent vector, the GM for λ1 is 1.
λ2 = 3, which has an algebraic multiplicity (AM) of 1. To find the dimension of the corresponding eigenspace (GM), we solve the system (C - λ2I)x = 0. In this case, there is only one independent vector, so the GM for λ2 is also 1.
A matrix is diagonalizable if the sum of the dimensions of all eigenspaces (GM) equals the size of the matrix. In this case, the sum of GMs is 1 + 1 = 2, while the size of the matrix is 3x3. Therefore, the matrix C is not diagonalizable.
Your answer:
λ1 = 0, AM = 2, GM = 1
λ2 = 3, AM = 1, GM = 1
Matrix C is NOT diagonalizable.
Visit here to learn more about eigenvalues:
brainly.com/question/31650198
#SPJ11
George wants to invest his money such that he accumulates $10,000 after 3 and half years at a rate of 4% compounded monthly? How much money should he invest daily?
Answers
Answer:
$8.77Step-by-step explanation:
Using the compound interest formula \(A = P(1+\frac{r}{n} )^{nt}\)
A = amount compounded (in $)
P = Principal (in $)
r = rate (in %)
t = time it takes to accumulate fund (in years)
n = time of compounding (in years)
Given P = $10,000, r = 4%, t = 3.5 years n = 1/12 years (since it is compounded monthly)
\(A = 10000(1+\frac{0.04}{(1/12)} )^{(3.5)(1/12)}\\A = 10000(1+0.48)^{0.2916}\\A = 10000(1.48)^{0.2916}\\A = 10000*1.12111\\A = 11,211.1\)
Amount he will compound after 3.5years will be $11,211.1.
Amount he should invest daily = Amount compounded/time taken (in days)
Since 3.5years ≈ 1278 days
Amount he should invest daily = $11,211.1/1278
Amount he should invest daily = $8.77
Which of the following goals is NOT a long-term goal?
saving for the down payment on a house
saving for a weekend vacation
saving for retirement
saving for higher education such as college
Answers
Answer:
Saving for a weekend vacation
Step-by-step explanation:
The goals that should not have the long-term goal should be considered is the saving for the weekend vacation.
What is long term goal?A long-term goal should be that arise in the near future. It plays a vital role for the successful carrer. Also, it is something which needs to achieve in near future. It needs the time and planning.
Here in the given situation, the saving for the down payment, retirement for the higher education these all represents the long term goal.
Therefore, the second option is correct.
Learn more about retirement here: https://brainly.com/question/24597215
PLS HELP IM STRUGGLING!!!!!!

Answers
Answer:
i think ist D correct me if im wrong
Step-by-step explanation:
Answer:
22.7
Step-by-step explanation:
if ∡M is 90° then you can do:
sin 65 = h/25
h = 25(sin 65°)
h = 22.65
if x=-2, y=-6 and z=4, Find the value of 4xy 3marks
Answers
Answer:
Step-by-step explanation:
4xy=4*(-2)*(-6)
4xy=48
Suppose an insurance company wants to determine the average speed of cars passing through an intersection. They randomly selected 85 cars and found their average speed to be 42 miles per hour with standard deviation of 4.2 miles per hour. A 90% confidence interval for the average speed of all the cars passing through the intersection is
Answers
The 90% confidence interval for the average speed of all the cars passing through the intersection is (41.29, 42.71) miles per hour.
To calculate the confidence interval, we can use the formula:
Confidence interval = Sample mean ± (Critical value * Standard error)
Given that the sample mean is 42 miles per hour and the standard deviation is 4.2 miles per hour, we need to determine the critical value and the standard error.
Since we have a sample size of 85, we can use the t-distribution with (n-1) degrees of freedom to find the critical value. With a 90% confidence level, the corresponding critical value for a two-tailed test is approximately 1.66.
The standard error is calculated as the standard deviation divided by the square root of the sample size:
Standard error = (Standard deviation) / √(Sample size)
Standard error = 4.2 / √85 ≈ 0.456
Now we can plug in the values into the confidence interval formula:
Confidence interval = 42 ± (1.66 * 0.456)
Confidence interval ≈ (41.29, 42.71)
Therefore, the 90% confidence interval for the average speed of all the cars passing through the intersection is (41.29, 42.71) miles per hour.
Based on the given data and calculations, we can conclude that with 90% confidence, the average speed of all the cars passing through the intersection falls within the range of 41.29 to 42.71 miles per hour.
To know more about intersection , visit :
https://brainly.com/question/12089275
#SPJ11
Find all zeros and write the polynomial as a product of linear factors
P(x) = x^3 -5x^2 + 2x +12
Show work please
Answers

Luis has an account at GESA Credit Union. He had a balance of $500.00 starting January 15th. He made deposits of $100, $250, and $300. He also made withdrawals of $400.32, $100, $55.55, and $62.62. What would be his ending balance after all the transactions?
SHOW THE WORK PLEASE
Answers
Answer:
the ending balance is $531.51
Step-by-step explanation:
The computation of the ending balance is shown below:
= Opening balance + all deposits - all withdrawls
= $500 + $100 + $250 + $300 - $400.32 - $100 - $55.55 - $62.62
= $531.51
hence, the ending balance is $531.51
Karen is at least 4 years more than twice mary's age (m). Karen is 46 years old. Write a simplified inequality that represents marys age answer
Answers
Answer:
46 ≥ 2m + 4
m ≥ 21
Step-by-step explanation:
At least is ≥
Karen's age = 46 years old
Mary's age = m years old
Karen is at least 4 years more than twice mary's age (m).
46 ≥ 2m + 4
46 - 4 ≥ 2m
42 ≥ 2m
m ≥ 42/2
m ≥ 21
The probability that maria succeeds at any given free-throw is 75\%75%75, percent. She was curious how many free-throws she can expect to succeed in a sample of 101010 free-throws. She simulated 252525 samples of 101010 free-throws where each free-throw had a 0. 750. 750, point, 75 probability of being a success. Maria counted how many free-throws were successes in each simulated sample. Here are her results:.
Answers
The probability of Maria succeeding is 0.2.
Probability is the branch of discrete mathematics. It is used for calculating how likely an event is to occur or happen.
P( E ) = number of favourable outcomes / number of total outcomes → 1
The results from the 25 samples showing success in each of the 10 trial throws:
10 successes - 1 outcome9 successes - 5 outcomes8 successes - 6 outcomes7 successes - 8 outcomes6 successes - 5 outcomes5 successes - 0 outcomeMaria succeeds fewer than 7 times i.e. 5 and 6 times for 0 + 5 = 5 outcomes.
The probability of Maria succeeding at fewer than 7 throws in a sample of 10 free throws,
Number of favourable outcomes = 5 → (i)
Number of total outcomes = 25 → (ii)
Substitute (i) and (ii) in 1,
P( E ) = 5 / 25
= 1 / 5
P( E ) = 0.2
To know more about probability problems refer to:
https://brainly.com/question/24756209
#SPJ4
The complete question is

Which equation represents the partial sum of the geometric series?
125 + 25 + 5 + 1
25 + 5 + 1 + one-fifth
1 + one-fifth + StartFraction 1 Over 25 EndFraction + StartFraction 1 Over 125 EndFraction
StartFraction 1 Over 125 EndFraction + one-fifth + 5 + 125
Answers
The partial sum of the geometric series is:
125 + 25 + 5 + 1
Option First is true.
What is Geometric series?
Geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. The formula for calculating the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence is known as the geometric series formula. The series has the following notation: a, ar, ar2, ar3,... where r is the "common ratio" and an is the first term
Given that;
The geometric series.
∑ 125 (1/5)ⁿ⁻¹ ; where, n = 1 to 4.
Now, Calculate the partial sum of the geometric series as;
The geometric series = ∑ 125 (1/5)ⁿ⁻¹
Substitute n = 1, 2, 3, 4, we get;
= 125 (1/5)¹⁻¹ + 125 (1/5)²⁻¹ + 125 (1/5)³⁻¹ + 125 (1/5)⁴⁻¹
= 125 (1/5)⁰ + 125 (1/5)¹ + 125 (1/5)² + 125 (1/5)³
= 125 + 25 + 125/25 + 125/125
= 125 + 25 + 5 + 1
Thus, The partial sum of the geometric series 125+ 25 + 5 + 1
Option A is true.
Learn more about the geometric series visit: brainly.com/question/5220881
#SPJ4
What point is a reflection of (-4, -9) across the x-axis?
Answers
is translation a and b?
Answers
where a is the number of units to move right or left along the x-axis and b is the number of units to move up or down along the y-axis.
40
Why are the solutions to the proportions 8
=
х
and
40
10
8 the same?
10
O because both result in the equation 8X= 400, which simplifies to X = 5
O because both result in the equation 8x=400, which simplifies to x = 50
O because both result in the equation 40x=80, which simplifies to X = 2
O because both result in the equation 40x = 80, which simplifies to X = 20

Answers
Answer:
B.
Step-by-step explanation:
They both have the same solution because both end up having
=> 8x = 500
Which is further simplified into
=> x = 50
find the area of the polygon with the given points A (-5,-2) B (4,-2) C (4, -7) D (-5, -7)
Answers
Step by step
It’s a rectangle!
9 units long (x axis) by 5 units tall (y axis)
= 45 units squared

andrew is riding his bike. he biked a distance of 14 miles at a rate of 7 miles per hour. using the distance formula, d
Answers
According to the question It took Andrew 2 hours to bike a distance of 14 miles at a rate of 7 miles per hour.
Using the distance formula, we can calculate the time it took for Andrew to bike a distance of 14 miles at a rate of 7 miles per hour. The formula for distance is:
Distance = Rate × Time
Rearranging the formula to solve for time:
Time = Distance / Rate
Plugging in the given values:
Time = 14 miles / 7 miles per hour
Time = 2 hours
Therefore, it took Andrew 2 hours to bike a distance of 14 miles at a rate of 7 miles per hour.
To know more about rate visit -
brainly.com/question/12892661
#SPJ11
A _____ measures the dispersion around the expected value.
A. standard deviation
B. mean
C. coefficient of variation
D. chi square
Answers
The correct answer is A. Standard deviation measures the dispersion or variability around the expected value or mean of a data set. It is a commonly used statistical measure to quantify the spread of data points.
Standard deviation is calculated by taking the square root of the variance. The variance is the average of the squared differences between each data point and the mean. By squaring the differences, negative values are eliminated, ensuring that the measure of dispersion is always positive.
A higher standard deviation indicates greater variability or dispersion of data points from the mean, while a lower standard deviation suggests that the data points are closer to the mean.
On the other hand, the mean (option B) is a measure of central tendency that represents the average value of a data set. It does not directly measure the dispersion or variability around the mean.
The coefficient of variation (option C) is a relative measure of dispersion that is calculated by dividing the standard deviation by the mean. It is useful for comparing the relative variability between different data sets with different scales or units.
The chi-square test (option D) is a statistical test used to determine if there is a significant association between categorical variables. It is not a measure of dispersion around the expected value.
For more such questions on standard deviation.
https://brainly.com/question/24298037
#SPJ8
Evaluate the integral by reversing the order of integration 7/2 cosx V1+cosx dc dụ.
Answers
The evaluated integral is (7/4) (π - (3√3)/6) (rounded to an appropriate decimal approximation based on the given values of π and √3).
To evaluate the integral ∫∫(7/2 cos(x)) dV, where the region of integration is given by V: 1 ≤ c ≤ 2 and 0 ≤ x ≤ cos⁻¹(2c-1), we can reverse the order of integration.
Step 1: Write the integral with reversed order of integration:
∫∫(7/2 cos(x)) dc dx
Step 2: Determine the limits of integration for the reversed order. The variable c now varies from 1 to 2, and x varies from 0 to cos⁻¹(2c-1). Therefore, the integral becomes:
∫[1,2] ∫[0,cos⁻¹(2c-1)] (7/2 cos(x)) dx dc
Step 3: Integrate with respect to x first. The integral with respect to x is straightforward:
∫[1,2] [sin(x)] [0,cos⁻¹(2c-1)] (7/2) dc
Step 4: Evaluate the inner integral:
∫[1,2] [sin(cos⁻¹(2c-1))] (7/2) dc
Step 5: Simplify the inner integral using the trigonometric identity sin(cos⁻¹(u)) = √(1 - u²):
∫[1,2] [√(1 - (2c-1)²)] (7/2) dc
Step 6: Integrate with respect to c:
(7/2) ∫[1,2] [√(1 - (2c-1)²)] dc
Step 7: Evaluate the integral:
Using the trigonometric substitution u = sin(t), du = cos(t) dt, and the limits change to t: π/6 ≤ t ≤ π/2.
(7/4) ∫[π/6, π/2] [√(1 - sin²(t))] cos(t) dt
Step 8: Simplify the integrand:
(7/4) ∫[π/6, π/2] [cos²(t)] dt
Step 9: Apply the double-angle formula for cosine:
(7/4) ∫[π/6, π/2] [(1 + cos(2t))/2] dt
Step 10: Split the integral into two separate integrals:
(7/4) [∫[π/6, π/2] (1/2) dt + ∫[π/6, π/2] (cos(2t)/2) dt]
Step 11: Integrate each term separately:
(7/4) [(t/2) + (sin(2t)/4)] evaluated from π/6 to π/2
Step 12: Substitute the limits and simplify:
(7/4) [((π/2)/2 + (sin(2(π/2))/4) - ((π/6)/2) - (sin(2(π/6))/4)]
Step 13: Simplify further:
(7/4) [(π/4 + 0 - π/12 - (1/4)(√3/2))]
Step 14: Simplify and calculate the final value:
(7/4) [(π/4 - π/12 - (√3/8))]
= (7/4) [(3π - π - 3√3)/12]
= (7/4) [(2π - 3√3)/12]
= (7/4) (π - (3√3)/6)
Learn more about the integral at
https://brainly.com/question/31059545
#SPJ4
It rained One and one-sixteenth inches on Saturday and 0.4 inches on Sunday. Which is the most reasonable estimate for the amount of rain that fell over two days?
0.5 inches
1.5 inches
2 inches
3 inches
Answers
Answer:
0.5 Inches
Step-by-step explanation:
1/16=.0625 which is about .1 for estimating purposes
.1 on Saturday + .4 on Sunday = .5 inches of rain over the two days
Answer: 1.5 inches
Step-by-step explanation:
"The amount of rain that fell over two days" means the sum of the two amounts of rain that fell on Saturday and Sunday.
\(1\frac{1}{16} +0.4=1\frac{10}{160} + \frac{4}{10} = 1\frac{10}{160} + \frac{64}{160} = 1\frac{74}{160}\)
This number is close to \(1\frac{80}{160}\), which is 1.5 inches.
A pipe is leaking at a rate of 9
gallons per second. How fast is this
quarts per minute?
Q) 1840 qt/min
s) 1890 qt/min
FYRST.
R) 2160 qt/min
T) 2060 qt/min
Answers
Answer:
2160
Step-by-step explanation:
9×60×4 = 2160 because there is 60 seconds in a minute and 4 quarts a gallon
Peter says 3/4 of a pizza is always the same as 6/8 of a pizza. Nadia says while 3/4 and 6/8 are equivalent fractions, 3/4 and 6/8 of a pizza could represent different amounts.
PLEASE HELP ASAP I HAVE 3 MINS LEFT!!!
PLEASE ANSWER THE PICTURE I SENT YOU BECAUSE IT HAS TO DO WITH THE QUESTION.
JUST DO NUMBER 2

Answers
Peter is right and Nadia is wrong.
What are equivalent fractions?Equivalent fractions are fractions that represent the same value, even though they look different.
Given is that Peter says 3/4 of a pizza is always the same as 6/8 of a pizza. Nadia says while 3/4 and 6/8 are equivalent fractions, 3/4 and 6/8 of a pizza could represent different amounts.
{ 1 } -
3/4 = (3 x 2)/(4 x 2) = 6/8
Peter is right.
Now -
3/4 = 6/8
So it could not represent two different quantities. So, Nadia is wrong.
{ 2 } -
3/4 = 6/8 = 9/12 = 12/15
These all represent the same quantity. Division of all the expressions will result in same value.
Therefore, Peter is right and Nadia is wrong.
To solve more questions on equivalent fractions, visit the link below -
https://brainly.com/question/29775885
#SPJ1
someone please help I CAN'T SOLVE THIS I NEED TO FIND M AND Z
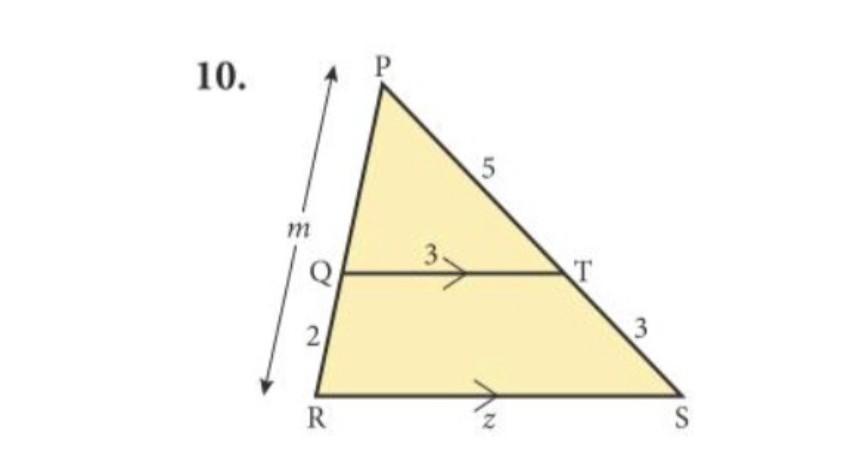
Answers
Answer:
m = \(\frac{16}{3}\) , z = \(\frac{24}{5}\)
Step-by-step explanation:
Δ PQT and Δ PRS are similar ( by AA postulate ), so the ratios of corresponding sides are equal, that is
\(\frac{PQ}{PR}\) = \(\frac{PT}{PS}\) , substitute values
\(\frac{m-2}{m}\) = \(\frac{5}{8}\) ( cross- multiply )
8(m - 2) = 5m ← distribute parenthesis on left side
8m - 16 = 5m ( subtract 5m from both sides )
3m - 16 = 0 ( add 16 to both sides )
3m = 16 ( divide both sides by 3 )
m = \(\frac{16}{3}\)
and
\(\frac{QT}{RS}\) = \(\frac{PT}{PS}\) , substitute values
\(\frac{3}{z}\) = \(\frac{5}{8}\) ( cross- multiply )
5z = 24 ( divide both sides by 5 )
z = \(\frac{24}{5}\)
