What is the awnser
5+5 =?
Answers
Answer:
10
Step-by-step explanation:
Answer:
10
Step-by-step explanation:
Related Questions
help please help asap :)

Answers
Answer:
4x^3
Step-by-step explanation:
20 x^5 + 28 x^4 + 12x^3
4*5*x^5 + 4*7*x^4 + 4*3*x^3
Factor out 4x^3
4x^3 ( 5x^2 + 7x +3)
help
(5a-3a^3)*(4a-1)
Answers
Answer:
\(-12a^{4} + 3a^{3} + 20a^{2} -5a\)
Step-by-step explanation:
\((5a-3a^{3} )\) • \((4a-1)\)
Let's use FOIL (first, outer, inner, last) to solve this. We'll multiply the terms by one another in that fashion.
\(20a^{2} - 5a - 12a^{4} + 3a^{3}\)
Rearrange in decreasing exponents.
\(-12a^{4} + 3a^{3} + 20a^{2} -5a\)
Lance is drawing a triangle. He draws one
side that is 8 inches long and another side
Se that is 5 inches long. Which one of the yeu
following could be the third side?
Answers
The possible lengths for the third side could be: any length between 1 inch and 12 inches (but not equal to either 8 inches or 5 inches) any length greater than 12 inches
What is triangle ?
Triangle can be defined in which it consists of three sides , three angles and sum of three angles is always 180 degrees.
Given ,
Lance is drawing a triangle. He draws one side that is 8 inches long and another side Se that is 5 inches long.
The third side of the triangle can be any length that satisfies the triangle inequality theorem. According to this theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
So, in Lance's triangle, if the first side is 8 inches long and the second side is 5 inches long, then the third side must be less than 8 + 5 = 13 inches.
So, the possible options for the third side are:
6 inches
7 inches
9 inches
10 inches
11 inches
12 inches
13 inches or longer.
Therefore, The possible lengths for the third side could be: any length between 1 inch and 12 inches (but not equal to either 8 inches or 5 inches) any length greater than 12 inches
To learn more about Triangle from given link.
https://brainly.com/question/2773823
#SPJ1
Consider the following vector field.
F(x, y, z) =
9ex sin(y), 2ey sin(z), 8ez
sin(x)
(a)
Find the curl of the vector field.
curl(F) =
(b)
Find the divergence of the vector field.
div(F) =
Answers
The curl of the vector field
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
The divergence of the vector field
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
To find the curl of the vector field F(x, y, z) = 9ex sin(y), 2ey sin(z), 8ez sin(x), we need to compute the determinant of the curl matrix.
(a) Curl of F:
The curl of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
curl(F) = (∂R/∂y - ∂Q/∂z)i + (∂P/∂z - ∂R/∂x)j + (∂Q/∂x - ∂P/∂y)k
In this case, we have:
P(x, y, z) = 9ex sin(y)
Q(x, y, z) = 2ey sin(z)
R(x, y, z) = 8ez sin(x)
Taking the partial derivatives, we get:
∂P/∂y = 9ex cos(y)
∂Q/∂z = 2ey cos(z)
∂R/∂x = 8ez cos(x)
∂R/∂y = 0 (no y-dependence in R)
∂Q/∂x = 0 (no x-dependence in Q)
∂P/∂z = 0 (no z-dependence in P)
Substituting these values into the curl formula, we have:
curl(F) = (0 - 2ey cos(z))i + (8ez cos(x) - 0)j + (0 - 9ex cos(y))k
= -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
Therefore, the curl of the vector field F is given by:
curl(F) = -2ey cos(z)i + 8ez cos(x)j - 9ex cos(y)k
(b) Divergence of F:
The divergence of a vector field F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k is given by the following formula:
div(F) = ∂P/∂x + ∂Q/∂y + ∂R/∂z
In this case, we have:
∂P/∂x = 9e^x sin(y)
∂Q/∂y = 2e^y sin(z)
∂R/∂z = 8e^z
Substituting these values into the divergence formula, we have:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Therefore, the divergence of the vector field F is given by:
div(F) = 9e^x sin(y) + 2e^y sin(z) + 8e^z
Learn more about divergence of the vector this link:
https://brainly.com/question/30907324
#SPJ11
a round pizza was cut into 9 sectors whose central angles are in the ratio of 1:2:3:4:5:6:7:8:9. what is the central angle of the largest piece?
Answers
The sum of the central angles is 360 degrees. If the ratios are 1:2:3:4:5:6:7:8:9, the sum of the ratios is 45. The central angle of the largest piece is 360 degrees / 45 = 8 degrees.
A round pizza cut into 9 sectors has its central angles in the ratio of 1:2:3:4:5:6:7:8:9. This means that the central angle of each sector is proportional to the ratio assigned to it. The sum of the central angles of all the sectors is 360 degrees, which represents a complete circle. The sum of the ratios is 45, which indicates that the central angle of each sector can be calculated by dividing 360 by 45. The central angle of the largest sector, which has a ratio of 9, is 360 divided by 45, which equals 8 degrees. In conclusion, the central angle of the largest sector of the pizza is 8 degrees.
To learn more about central angle visit: https://brainly.com/question/10945528
#SPJ4
What does y equal? A. 51 B. 39 C. 37
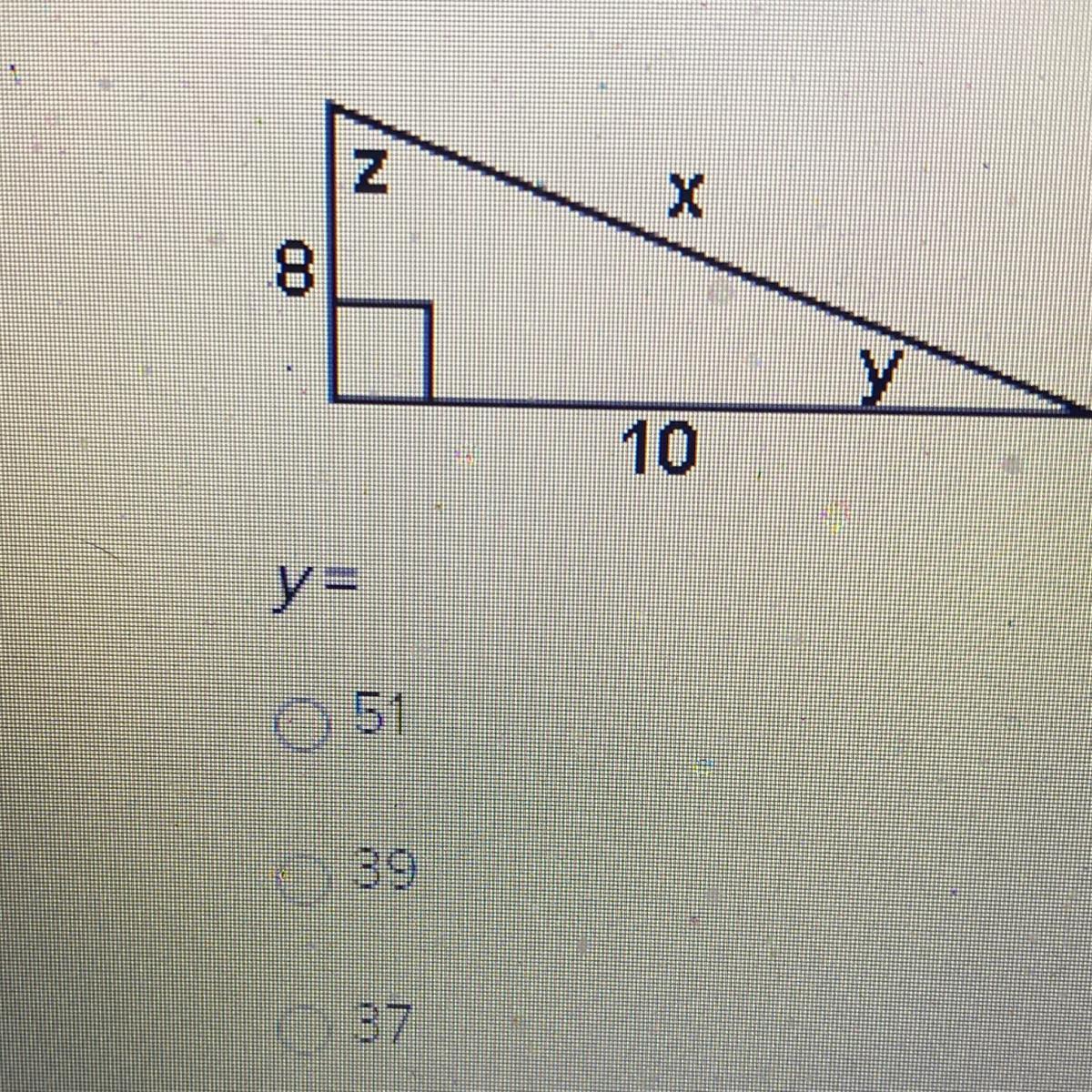
Answers
Answer:
B. 39°
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
BracketsParenthesisExponentsMultiplicationDivisionAdditionSubtractionLeft to RightAlgebra I
Equality PropertiesGeometry
[Right Triangles Only] SOHCAHTOA[Right Triangles Only] tanθ = opposite over adjacentStep-by-step explanation:
Step 1: Identify
Angle θ = y
Opposite Leg = 8
Adjacent Leg = 10
Step 2: Solve for y
Substitute [Tangent]: tan(y) = 8/10Simplify: tan(y) = 4/5Inverse Trig: y = tan⁻¹(4/5)Evaluate: y = 38.6598Round: y ≈ 39°f(x1, x2) 421 +222 3x² +213 5x11² (√₁+√₂)² 10ln(₁) (x₁+x₂)(x² + x3) min(3r1, 10√2) max{5x1,2r2} MP1(x1, x₂) MP2(X1, X₂) TRS(x1, x₂) Output (2,4)
Answers
The given mathematical expression is evaluated for the input values (2, 4). The result of the expression is calculated using various operations such as addition, multiplication, square root, natural logarithm, minimum, maximum, and function composition.
The expression f(x1, x2) involves several mathematical operations. Let's evaluate each part of the expression step by step:
1. The first term is 421 + 222, which equals 643.
2. The second term is 3x² + 213. Plugging in x1 = 2 and x2 = 4, we get 3(2)² + 213 = 3(4) + 213 = 12 + 213 = 225.
3. The third term is 5x11². Substituting x1 = 2 and x2 = 4, we have 5(2)(11)² = 5(2)(121) = 1210.
4. The fourth term is (√₁+√₂)². Replacing x1 = 2 and x2 = 4, we obtain (√2 + √4)² = (1 + 2)² = 3² = 9.
5. The fifth term is 10ln(₁). Plugging in x1 = 2, we have 10ln(2) = 10 * 0.69314718 ≈ 6.9314718.
6. The sixth term is (x₁+x₂)(x² + x3). Substituting x1 = 2 and x2 = 4, we get (2 + 4)(2² + 4³) = 6(4 + 64) = 6(68) = 408.
7. The seventh term is min(3r1, 10√2). As we don't have the value of r1, we cannot determine the minimum between 3r1 and 10√2.
8. The eighth term is max{5x1,2r2}. Since we don't know the value of r2, we cannot find the maximum between 5x1 and 2r2.
9. Finally, we have MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2), which are not defined or given.
Considering the given expression, the evaluated terms for the input values (2, 4) are as follows:
- 421 + 222 = 643
- 3x² + 213 = 225
- 5x11² = 1210
- (√₁+√₂)² = 9
- 10ln(₁) ≈ 6.9314718
- (x₁+x₂)(x² + x3) = 408
The terms involving min() and max() cannot be calculated without knowing the values of r1 and r2, respectively. Additionally, MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2) are not defined.
To learn more about logarithm click here: brainly.com/question/30226560
#SPJ11
over what interval does f(x)=2^x increase faster than g(x)=8/3x
Answers
Using exponential function concepts, it is found that f(x) increases faster than g(x) on the interval of 0 < x < 1.
What is an exponential function?An exponential function is modeled by:
\(y = ab^x\)
In which:
a is the initial value.b is the rate of change.In the interval of 0 < x < 1, a lower value of b leads to a greater change, while for x > 1, a higher value of b leads to greater change.
In this problem, the functions are:
\(f(x) = 2^x\)
\(g(x) = \left(\frac{8}{3}\right)^x\)
Hence:
\(b_f = 2\(
\(b_g = \frac{8}{3}\)
Since \(b_g > b_f\), f(x) increases faster than g(x) on the interval of 0 < x < 1.
More can be learned about exponential function concepts at https://brainly.com/question/25537936
a $45 pair of rainboots is on sale for $38.2. what percent does the customer save?
Answers
Answer:
Step-by-step explanation:
Discount = 45 - 38.20 = $ 6.80
Discount % = \(\frac{Disscount}{Original price}*100\)
= \(\frac{6.80}{45}*100\)
= 15.11 %
Percentage of savings = 15.11%
Find the circumference and area of the circle of radius 4.2 cm.
Answers
The circumference of the circle is 26.4 cm and the area of the circle is 55.3896 cm².
The circumference and area of a circle of radius 4.2 cm can be calculated using the following formulas:
Circumference = 2πr, where r is the radius of the circle and π is a constant approximately equal to 3.14.
Area = πr², where r is the radius of the circle and π is a constant approximately equal to 3.14.
Circumference = 2πr = 2 × 3.14 × 4.2 cm = 26.4 cm
Area = πr² = 3.14 × (4.2 cm)² = 55.3896 cm²
Given the radius of the circle as 4.2 cm, the circumference of the circle can be found by using the formula for the circumference of a circle. The circumference of a circle is the distance around the circle and is given by the formula C = 2πr, where r is the radius of the circle and π is a constant approximately equal to 3.14. By substituting the given value of r, the circumference of the circle is calculated as follows:
Circumference = 2πr = 2 × 3.14 × 4.2 cm = 26.4 cm
Similarly, the area of the circle can be found by using the formula for the area of a circle. The area of a circle is given by the formula A = πr², where r is the radius of the circle and π is a constant approximately equal to 3.14. By substituting the given value of r, the area of the circle is calculated as follows:
Area = πr² = 3.14 × (4.2 cm)² = 55.3896 cm²
Therefore, the circumference of the circle is 26.4 cm and the area of the circle is 55.3896 cm².
To know more about the circumference visit:
https://brainly.com/question/402655
#SPJ11
jacob and elizabeth are 210 feet apart when they begin walking directly toward one another. jacob travels at a constant speed of 2.5 feet per second and elizabeth travels at a constant speed of 4.5 feet per second. let t represent the number of seconds that have elapsed since jacob and elizabeth started walking toward one another. write an expression in terms of t that represents the number of feet jacob has traveled since he started walking toward elizabeth.
Answers
The number of feet Jacob has traveled since he started walking toward Elizabeth is 2.5t .
Let the distance between Jacob and Elizabeth is 210 feet
Distance = speed x time
Jacob is walking at the constant speed of 2.5 feet per second
and Elizabeth is walking at a constant speed of 4.5 feet per second
Let the distance traveled by jacob be x and distance traveled by Elizabeth be (210 - x)
Let t be time passed when they both started walking towards each other
So the time taken by Jacob to cover x amount of distance is t
so by formula Distance = speed x time
x = 2.5 x t
So number of feet jacob has traveled since he started walking toward elizabeth is 2.5t.
Distance is a measurement of how far apart two things or points are, either numerically or occasionally qualitatively. Distance can refer to a physical length in physics or to an estimate based on other factors in common usage.
Learn more about Time, Speed, Distance:
https://brainly.com/question/26046491
#SPJ4
Your friend writes 1.475% as a decimal. Is your friend correct? Explain your reasoning. 1.475% = 1.475% = 147.5
Answers
Answer:
no because the decimal doesn't have a % sign its 147.5
answerrrrrr plssss ill giveee brainliesttttt

Answers
\(m\angle E=\sin \dfrac{\sqrt{10}}{2\sqrt5}=\sin \dfrac{\sqrt2}{2}=45^{\circ}\)
abc is a right triangle with ab=ac. bisector of <a meets bc at d. prove that bc = 2ad.
Answers
Answer:
Let ac=ab=5
With this, bc= 5√2
Step-by-step explanation:
So to find ad, Let ad be x
5√2=(2)(x)
(5√2/2)= x
This proves that bc=2ad

What conclusion could be drawn from the following premises and by what rule (excluding Add., Simp., and Conj.)?² 1. (~Av~B)~(Cv~D), ~AV~B 1.. 2. (Av B) D (~B vC), ~(~BVC) (Av~B) /.. 3. ~(Av~ B), (~A~B) v (Av~B) 1. 4. (CVD). (~(Cv~D) v~C) (Cv~D) /.. 5. (E=~F) v (F= (~E~F)), ~(E = ~F) 1.. 6. ~AD (Bv~C), ~Av (~Bv~C). (~BV~C) (~Av(Cv~B)) /.. 7. (~AD (~Bv~A)) (ADB),~(A~B) /.. 8. (ADB) D (AD (CDA)), (CD (ADC)) (ADB) /.. 9. ~ (Cv (AVC))~(AD (CDA)), ~(CV(AVC)) /.. 10. (CV(AVC)) v (~Av~C), ~(~Av~C) 1. N
Answers
From the given premises, the following conclusions can be drawn:
(AvB)
~(~BVC)
(AB) v (Av~B)
((CvD) v~C)
~(E = ~F)
(BVC)
~ (A~B)
(CD (ADC))
~(CV(AVC))
~(AvC)
From premise 1, using De Morgan's law, we can conclude (AvB).
From premise 2, applying De Morgan's law, we get ~(~BVC).
By simplifying the expression in premise 3, we obtain (AB) v (Av~B).
By simplifying the expression in premise 4, we get ((CvD) v~C).
From premise 5, we can conclude ~(E = ~F).
From premise 6, we obtain (BVC).
Using double negation, we can conclude ~ (A~B) from premise 7.
From premise 8, applying Commutation, we get (CD (ADC)).
From premise 9, we have ~(CV(AVC)).
By simplifying the expression in premise 10, we obtain ~(AvC).
The conclusions are derived from the given premises using logical rules such as De Morgan's law, double negation, Commutation, and simplification. These rules allow us to manipulate the expressions and derive logical conclusions based on the given information.
To learn more about simplificationclick here:
brainly.com/question/23509407
#SPJ11
9. There are 56 children who need to be divided into teams of 8. How many children will
be on each team? What is this problem asking you?
PLEASE HELP I NEED TO KNOW ASAPPP!!! :(
problem 9.

Answers
Answer:
Your answer is 7 children on each team
Step-by-step explanation:
The question clearly states "divided," so divide 56 by 8.
The question is asking you how many kids are on each team.
If I didn't understand the question properly, let me know. :) good luck!
yumiko solved |x|>5 by solving x>-5 and x<5. explain the error yumiko made
Answers
Answer:
switched signs around
Step-by-step explanation:
I believe that s/he switched the signs around so
|x|>5 is solved by x<-5 and x>5
but I'm not quite sure, sorry
Please show work;) goodnight also

Answers
Answer:
k f78iiujyhtgrf
Step-by-step explanation:
Use the distributive property to simplify the following expression: 7(4 - 3x)
1.28 - 3x
2.7x
3.28 - 21x
4.21x
Answers
Answer: 3. 28-21x
Step-by-step explanation: distribute the 7 to both 4 and -3x
7 x 4= 28
7 x -3x = -21x
28-21x
Hope this helps (^_^)
Answer:
28 - 21x
Step-by-step explanation:
7(4 - 3x)
7×4 = 28
7× -3x = -21x
If a projectile is launched vertically upward from 800 ft above the ground with an initial velocity of 80 ft per second, its height in feet t seconds after launch is given by s=−16t2+80t+800
.
The projectile will take _____ seconds to return to the ground.
After _______ seconds, the projectile will be 576 feet above the ground.
Answers
Hello!
10 seconds to return to the ground.
7 seconds to reach 576 feet above the ground.
Find the amount of time taken to reach the ground by setting the equation equal to 0:
0 = -16t² + 80t + 800
Factor out -16 from the equation:
0 = -16(t² - 5t - 50)
Factor the terms inside of the parenthesis:
0 = -16(t - 10)(t + 5)
Find the zeros:
t - 10 = 0
t = 10
t + 5 = 0
t = -5
Time can only be positive in this instance, so the correct answer is 10 sec.
Find the time by substituting in 576 for the height:
576 = -16t² + 80t + 800
Subtract 800 from both sides:
-224 = -16t² + 80t
Rearrange:
0 = -16t² + 80t + 224
Simplify:
0 = -16(t² - 5t - 14)
0 = -16(t - 7)(t + 2)
t = 7 seconds.
Example 1: What is the probability of choosing a marble
2 questions with stripes? What is the complement of
choosing a marble with no design?
P(stripes)
P'(no design?
Answers
Answer:
The probability of choosing a marble with stripes, P(stripes), would be 0.2. The complement of choosing a marble with no design, P'(no design), would also be 0.2.
Step-by-step explanation:
1. The probability of choosing a marble with stripes, P(stripes), would depend on the proportion of marbles with stripes in the overall population of marbles available to choose from.
2. If, for example, there are 20 marbles with stripes and 80 marbles without stripes in a set of 100 total marbles, the probability of choosing a marble with stripes would be 20/100, or 0.2.
3. The complement of choosing a marble with no design, P'(no design), would be the probability of choosing a marble with stripes, or P(stripes).
4. This is because the complement of an event is the probability of the event not occurring.
5. So, if the probability of choosing a marble with stripes is 0.2, the probability of not choosing a marble with stripes (i.e. choosing a marble with no design) would also be 0.2.
Suppose that there are 5 children in a gymnastics class. One day, they count the number steps each person takes while walking on their hands until they lose their balance and come down. The results are:
Chloe (20), Michael (8), Helen (22), Joshua (26), and Laura (24).
The mean number of steps these children took while walking on their hands is 20 steps.
(a) Identify the population and the parameter.
(b) List all 10 possible SRSs of size n=2. Calculate the mean number of steps taken while walking on their hands for each sample.
(c) Display the sampling distribution of the sample mean on a dotplot
Answers
a) A population is the number of children in gymnastic class = 5.
b) The parameter is the mean number of steps taken by the 5 children.
c) Parameters on the other hand are statistical metrics, values, or calculations derived from the population figure or information. Here, the mean value of steps obtained from the step counts of the population data is called the parameter.
The descriptive measurements of a whole population are called parameters. However, because it is impossible to measure a population as a whole, its values are typically unknown. As a result, you can acquire parameter estimates by selecting a random sample from the population.
The whole number or collection of comparable objects or persons connected to a certain study or research could be referred to as the population.
In the case above, a specific gymnastics class is the focus, hence the population is made up of all people or kids who participate in this particular gymnastics class.
On the other hand, statistical measures, values, or calculations that are produced from population data are known as parameters.
Here, the mean value of steps obtained from the step counts of the population data is called the parameter.
A parameter is a value that describes a characteristic of an entire population, such as the population means.
The population means and standard deviation are two common parameters.
Hence, Population = the number of children in gymnastic class = 5.
Parameter = a mean number of steps taken by the 5 children.
To know more about Probability click the link given below.
brainly.com/question/23135833
#SPJ4
S0 = 0 is the initial position of the particle, and let Sn be the position of the particle at times n = 0, 1, 2, 3. . . The position Sn for n ≥ 1 can be thought of as a sum of random displacements: Sn = X1 + X2 +. . . + Xn. Assume the Xi ’s are i. I. D. With Range(Xi) = {−1, 0, 2}, P(Xi = k) = 1 3 for all k ∈ Range(X) (so note that there is a bit of a "drift" to the right). (a) What is the probability distribution of the position S2 = X1 + X2? (b) Compute P(S90,000 ≤ 29, 500); express the result in decimals
Answers
a) The probability distribution are P(S₂ = -2) = 1/9, P(S₂ = -1) = 2/9, P(S₂ = 0) = 1/9, P(S₂ = 1) = 2/9, P(S₂ = 2) = 2/9, P(S₂ = 3) = 2/9, P(S₂ = 4) = 1/9
b) The probability that the particle's position S90,000 is less than or equal to 29,500 is approximately 0.0571.
In this problem, we are given a particle's initial position S₀ = 0, and its position Sₙ after n time intervals, where the position is a sum of n independent and identically distributed random displacements X₁, X₂, ..., Xₙ. Each displacement Xᵢ can take on one of three values: -1, 0, or 2, with equal probability 1/3 for each.
(a) To find the probability distribution of S₂ = X₁ + X₂, we can enumerate all possible values of S₂ and compute their probabilities. The possible values of S₂ are -2, -1, 0, 1, 2, 3, 4, and their respective probabilities are:
P(S₂ = -2) = P(X₁ = -1, X₂ = -1) = (1/3)² = 1/9
P(S₂ = -1) = P(X₁ = -1, X₂ = 0) + P(X₁ = 0, X₂ = -1) = 2(1/3)² = 2/9
P(S₂ = 0) = P(X₁ = 0, X₂ = 0) = (1/3)² = 1/9
P(S₂ = 1) = P(X₁ = 2, X₂ = -1) + P(X₁ = -1, X₂ = 2) = 2(1/3)² = 2/9
P(S₂ = 2) = P(X₁ = 2, X₂ = 0) + P(X₁ = 0, X₂ = 2) = 2(1/3)² = 2/9
P(S₂ = 3) = P(X₁ = 2, X₂ = 1) + P(X₁ = 1, X₂ = 2) = 2(1/3)² = 2/9
P(S₂ = 4) = P(X₁ = 2, X₂ = 2) = (1/3)² = 1/9
(b) To compute P(S90,000 ≤ 29,500), we can use the Central Limit Theorem (CLT) to approximate the distribution of S90,000. The CLT states that the sum of a large number of independent and identically distributed random variables tends to follow a normal distribution, regardless of the underlying distribution of the individual variables. For n large enough, we have:
S90,000 ≈ N(μ, σ²), where μ = nE(X) and σ² = nVar(X)
Here, n = 90,000, E(X) = (-1 + 0 + 2)/3 = 1/3, and Var(X) = [(2-1/3)² + (-1-1/3)² + (0-1/3)²]/3 = 10/9. Therefore, we have:
μ = 90,000(1/3) = 30,000
σ² = 90,000(10/9) ≈ 100,000
Now, we can standardize the variable Z = (S90,000 - μ)/σ and use a standard normal table or calculator to find the probability:
P(S90,000 ≤ 29,500) = P(Z ≤ (29,500 - 30,000)/√100,000) ≈ P(Z ≤ -1.58) ≈ 0.0571 (rounded to four decimal places)
To learn more about distribution click on,
https://brainly.com/question/14690794
#SPJ4

How do you translate a horizontal graph?
Answers
To translate a horizontal graph, you need to adjust the x-axis. This can be done by shifting the graph to the left or right. Additionally, you can stretch or shrink the graph by adjusting the scale of the x-axis.
A horizontal graph is a type of graph that is used to represent data in a two-dimensional space. To translate a horizontal graph, you must adjust the x-axis. This can be done by shifting the graph to the left or right. Additionally, you can stretch or shrink the graph by adjusting the scale of the x-axis. This can be done by changing the number of points on the x-axis, or by making the intervals between points larger or smaller. When translating a graph, it is important to make sure that the y-axis remains unchanged as this will ensure that the data is accurately represented. Translating a horizontal graph is a useful way to compare and analyze data. It allows you to see how changes in one variable affect the other variables in the data set. It is also an essential skill for data analysis and is used in many different fields, such as finance and economics.
Learn more about graph here
https://brainly.com/question/17267403
#SPJ4
Write an integer for the situation. 15 degrees below normal
Answers
Answer:
It's -15 than normal
-2/5(10x-3)-8.4> -12.4 i need the answer quick
Answers
Answer:
x < \(\frac{10}{13}\)
Step-by-step explanation:
hope this helps :)
3/7 g=9 how do you do it?

Answers
The answer is g = 21
just multiply the fraction.
3 × 7 is 21.
Jonczyk Company is considering two different, mutually exclusive capital expenditure proposals. Project A will cost $454,000, has an expected useful life of 13 years and a salvage value of zero, and is expected to increase net annual cash flows by $68,000. Project B will cost $300,000, has an expected useful life of 13 years and a salvage value of zero, and is expected to increase net annual cash flows by $47,000. A discount rate of 9% is appropriate for both projects. Click here to view PV table.
Calculate the net present value and profitability index of each project. (If the net present value is negative, use either a negative sign preceding the number e.g. -45 or parentheses e.g. (45). Round present value answers to 0 decimal places, e.g. 125 and profitability index answers to 2 decimal places, e.g. 15.52. For calculation purposes, use 5 decimal places as displayed in the factor table provided, e.g. 1.25124.)
Answers
Net present value is a measure of profitability. The NPV of an investment is the net cash inflow received over the project's life, less the initial cash outflow, adjusted for the time value of money.
A higher NPV means the project is more lucrative. The profitability index measures the benefit-cost ratio of a project and is calculated by dividing the present value of future cash flows by the initial cash outflow. A profitability index greater than one indicates that the project will be profitable, whereas a profitability index less than one indicates that the project will not be profitable.
Calculation of Net Present Value (NPV) of Project AInitial Outlay = $454,000Net annual cash flows = $68,000Discount Rate = 9%Use the PV of an annuity of $1 table to determine the PV of net cash flows.Using the formula for NPV,NPV of Project A = PV of net cash flows – Initial OutlayNPV of Project A = 68,000 × 7.63930 – 454,000NPV of Project A = $56,201.85Calculation of Profitability Index of Project AProfitability Index of Project A = Present value of future cash flows / Initial OutlayProfitability Index of Project A = 68,000 × 7.63930 / 454,000Profitability Index of Project A = 1.14
Calculation of Net Present Value (NPV) of Project BInitial Outlay = $300,000Net annual cash flows = $47,000Discount Rate = 9%Use the PV of an annuity of $1 table to determine the PV of net cash flows.Using the formula for NPV,NPV of Project B = PV of net cash flows – Initial OutlayNPV of Project B = 47,000 × 6.10338 – 300,000NPV of Project B = $37,100.86Calculation of Profitability Index of Project BProfitability Index of Project B = Present value of future cash flows / Initial OutlayProfitability Index of Project B = 47,000 × 6.10338 / 300,000Profitability Index of Project B = 0.96
The NPV and profitability index calculations show that project A is the better investment since it has a higher NPV and profitability index than project B.
To know more about Net present value visit
https://brainly.com/question/32720837
#SPJ11
9a ^ 2 + 24a + 16
please send me the answer fast
Answers
Answer:
(3a +4)²
have a nice day!
two friends natasha and tricia share a sum of money in the ratio 5:3 respectively if tricia share was $126.75,calculate the total sum of money shared
Answers
Answer:
253.48
Step-by-step explanation:
Hello this is answer