Answers
Answer:
for the area of the Circle we use A=πd
A=3.14x12 A=37.68
for a rectangle it is A=ab
A=12x15 A=180
37.68+180=142.32
your answer is 142.32 m 2
Related Questions
(SAT Prep) Find the value of x.

Answers
The angle measure of x is 115°.
What is a parallelogram?A parallelogram is a four-sided shape with two sets of parallel sides, which means that opposite sides are both parallel and have equal length. Parallelograms also have opposite angles with the same measure, and their diagonals intersect at the midpoint and bisect each other. This results in the parallelogram being divided into two triangles that are congruent. Examples of parallelograms include rectangles, squares, and rhombuses, and they are commonly used in both geometry and everyday life, particularly in the design of buildings and other structures.
We can call this figure ACDEF. Let us join CB.
Now we can see that BDEF is a parallelogram. Opposite angles of a parallelogram are equal, hence ∠DBF = ∠DEF = x°
And also consider the triangle ABC,
∠BAC = 50°
∠ABC = 180 - ∠DBF = 180° - x° (linear pair)
∠ACB = 180 - ∠ACD = 180° - x° (linear pair)
We know that all the angles of a triangle adds up to 180°.
Using this we can find x°:
∠BAC + ∠ABC + ∠ACB = 180°
50° + 180° - x° + 180° - x° = 180°
-2x° + 410 = 180°
-2x° = 180° - 410° = -230°
x° = -230/ -2
x ° = 115°
To know more about parallelogram visit:
brainly.com/question/11220936
#SPJ1

Find the unit rate. Round to the nearest hundredth, if necessary.
$340 for 14 ft
The unit rate is $
Answers
well, from 340 down to 150, their difference is 190.
now, if we take 340 to be the 100%, what is 190 off of it in percentage?
(60) POINTS AND 5 STAR AND THANKS AND BRIAN-LIST!!!!!
The chart below describes the speed of four desktop printers.
Which printer is the fastest?
A Roboprint
B Voltronn
C Vantek Plus
D DLS Pro
6 A store sells bags of 12 apples for $3.60. What is the unit cost per apple?
A $0.30
B $0.33
C $3.33
D $3.60
Answers
Answer:
1. Send me the chart and ill get you the answer.
2. unit cost is $0.30
Step-by-step explanation:
2. $0.30
what is 5\sqrt(3ft *3\sqrt(12))
Answers
The solution of 5√3 × 3√12 = 30√3.
What is square root?Square root of a number is defined as the number in which the multiplication by itself gives the original number. That is the square root of 9 would be = 3 in which when multiplied by itself gives the original number being 9.
Other examples include √ 4 = 2, √ 25 = 5, √100 = 10.
To simplify the give expression;
5√3 × 3√12= 5√3 × 3√4×3
= 5√3 × 3×2√3
= 5√3 × 6 √3
= 30√3.
Learn more about square root here ;
https://brainly.com/question/28428939
#SPJ1
QUESTION IS DOW BELOW 5 POINTS EACH PLEASE HELP PLEASE HELP PLEASE HELP

Answers
a. Central angle in the circle is: Angle BAC
b. A major arc is: Arc BEC
c. A minor arc is: Arc BC
d. measure of arc BEC is: 260°
e. m(BC) = 100°
What is a Central Angle?A central angle has two of its sides as radii of the circle, forming an angle at the center of the circle, where the vertex is at the center of the circle.
What is a Major Arc?A major arc has a measure that is greater than 180 degrees. That is, it is more than half a circle (semicircle). Thus, measure of major arc > 180 degrees.
What is a Minor Arc?A minor arc has a measure that is less than 180 degrees. That is, it is not more than half a circle (semicircle). Thus, measure of minor arc < 180 degrees.
a. Central angle in the circle is: Angle BAC
b. A major arc in circle A is: Arc BEC
c. A major arc in circle A is: Arc BC.
d. Measure of arc BEC = 360 - 100 [according to the central angle theorem]
Measure of arc BEC = 260°.
e. Measure of angle BAC = 100° [given]
Measure of arc BC = angle BAC [according to the central angle theorem]
Measure of arc BC = 100°
Learn more about major and minor arcs on:
https://brainly.com/question/23498567
#SPJ1
the phone company charges $33 for having a smartphone plus $9.95 a month for 2gb. IF mark has only $146.43 to spend on a phone, how many months can he have the phone? inequalities
Answers
The number of months Mark can have the phone is given by the equation
A = 11.4 months
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the number of months be represented as = A
Now , the equation is
Now , the total amount with Mark = $ 146.43
The initial amount for the smartphone = $ 33
The amount per month for 2GB is = $ 9.95
So , the amount for A months = $ 9.95 ( A )
So , the equation will be
Initial amount for the smartphone + the amount for A months = total amount with Mark
Substituting the values in the equation , we get
33 + 9.95 ( A ) = 146.43 be equation (1)
On simplifying the equation , we get
Subtracting 33 on both sides of the equation , we get
9.95 ( A ) = 113.43
Divide by 9.95 on both sides of the equation , we get
A = 11.4 months
Therefore , the value of A is 11.4 months
Hence , the number of months is 11.4 months
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Which table represents a relation that's a non-function?




Answers
Answer:
The table in the attachment is the right option
Step-by-step explanation:
A table that represents a function must have exactly one y-value assigned to every x-value. In other words, a table that is a function cannot have any x-value (input) with two corresponding different y-values (outputs).
The table in the attachment below represents a relation that is non-function because it has two outputs, 5 and 7, that are assigned or corresponding to one input, 7.

What is the answer?? 3(b-5)<-2b
Answers
Answer:
b < 3
Step-by-step explanation:
3 ( b - 5 ) < - 2b
3 ( b ) - 3 ( 5 ) < - 2b
3b - 15 < - 2b
3b + 2b < 15
5b < 15
b < 15/5
b < 3
3(b-5)<-2b
3b<-2b+5
Add the 2b over.
5b<5
Divide by 5.
b<1
Check by plugging in.
3(1-5)<-2(1)
3(-4)<-2
-12<-2
1 is a possibly solution to the inequality.
Order from least to greatest

Answers
Answer:
-sqrt15, 1/4, 1.7, sqrt7
Step-by-step explanation:
-sqrt15 is in the negatives so it is lowest. 1/4 is 0.25, sqrt7=2..... and 1.7=1.7
Jolene invests her savings in two bank accounts, one paying 3 percent and the other paying 9 percent simple
interest per year. She puts twice as much in the lower-yielding account because it is less risky. Her annual
interest is 3120 dollars. How much did she invest at each rate?
Amount invested at 3 percent interest is $____
Amount invested at 9 percent interest is $___
Answers
Let's denote the amount Jolene invested at 3 percent interest as 'x' dollars. Since she put twice as much in the lower-yielding account, the amount she invested at 9 percent interest would be '2x' dollars.
To calculate the interest earned from each account, we'll use the formula: Interest = Principal × Rate × Time.
For the 3 percent interest account:
Interest_3_percent = x × 0.03
For the 9 percent interest account:
Interest_9_percent = 2x × 0.09
We know that the total annual interest is $3120, so we can set up the equation:
Interest_3_percent + Interest_9_percent = 3120
Substituting the above equations, we have:
x × 0.03 + 2x × 0.09 = 3120
Simplifying the equation:
0.03x + 0.18x = 3120
0.21x = 3120
Dividing both sides of the equation by 0.21:
x = 3120 / 0.21
x = 14857.14
Therefore, Jolene invested approximately $14,857.14 at 3 percent interest and twice that amount, $29,714.29, at 9 percent interest.
Answer:
Step-by-step explanation:
X is the amount invested at 6%
Y is the amount invested at 9%
0.06X + 0.09Y = 4998
X = 2Y
0.06(2Y) + 0.09Y = 4998
.12Y + 0.09Y = 4998
0.21Y = 4998
21Y = 499800
Y = 499800/21 = 23800
So X = 2*23800 = 47600
$47,600 is invested at 6% and $23800 is invested at 9%
What is the value of 3?

Answers
9514 1404 393
Answer:
3 ⇒ 12
Step-by-step explanation:
Apparently "a = b" in this case is used to mean f(a) = b. It appears as though the function is ...
f(x) = x(x+1)
Then f(3) = 3(3+1) = 3·4 = 12
_____
Additional comment
IMO this is a poor use of the equal sign, which should be reserved for situations where the left side expression has the same value as the right side expression.
what is the value of x? Hiking trails oak trail 125 degrees. pine trail x degrees. ash trail.

Answers
Graph the point on the graph.

Answers
Answer:
see below
Step-by-step explanation:
To graph this equation, start at the origin (0,0) since there is not y-intercept.
Because slope is characterized by rise/run ( i.e. how many units up or down depending on whether it is positive or negative and then however many units to the right.
Because the rise (up and down, numerator) is 1, we know that we will go up one unit.
The run (side to side, denominator) is 4, so we will go to the right 4 units.
This makes the first point (4, 1).
Continue doing this until you get an idea of the line and connect the points to get the graph
Answer:
Info down in Explaination
Step-by-step explanation:
To graph this equation, start at the origin (0,0) since there is not y-intercept.
Because slope is characterized by rise/run ( i.e. how many units up or down depending on whether it is positive or negative and then however many units to the right.
Because the rise (up and down, numerator) is 1, we know that we will go up one unit.
The run (side to side, denominator) is 4, so we will go to the right 4 units.
This makes the first point (4, 1).
Continue doing this until you get an idea of the line and connect the points to get the graph
Can someone help me do the long division of this please
Its
P-4 divided by 10p^3-45p^2+26p-33

Answers
Answer:
\(10p {}^{2} - 5p + 6 + \frac{ - 9}{p - 4} \)
Step-by-step explanation:
10p²-5p+6
p-4√10p³-45p²+26p-33
- 10p³-40p²
-5p²+26p
- -5p²+20p
6p-33
- 6p-24
-9
To be labeled as a jumbo egg, the egg is supposed to weigh 2.5 oz. Priya buys a carton of jumbo eggs as 2.4 oz. what is the percentage error?
Answers
ANSWER
4%
EXPLANATION
We want to find the perecntage error in the given situation.
Percentage error is given as:
\(\text{ \%error = }\frac{|x_2-x_1|}{x_1}\cdot\text{ 100}\)where:
x1 = expected value of weight
x2 = measured value of weight
The numerator represents the absolute value of the difference between the two weights.
Therefore, the percentage error is:
\(\begin{gathered} \text{ \%error = }\frac{|2.4\text{ - 2.5}|}{2.5}\cdot\text{ 100 = }\frac{|-0.1|}{2.5}\cdot\text{ 100} \\ \text{ \%error = }\frac{0.1}{2.5}\cdot\text{ 100 = 0.04 }\cdot\text{ 100} \\ \text{ \%error = 4\%} \end{gathered}\)The percentage error is 4%.
All the following are Perfect Squares except for which one?
198
121
81
64
Answers
Answer:
Step-by-step explanation:
198 is not a perfect square
All the given numbers are perfect squares except 198
The given numbers:
1981218164To find:
non perfect square number among the given numbersA perfect square is obtained by multiplying two equal integers
The perfect squares obtained by multiplying two equal integers are shown below.
64 = 8 x 8 (it is a perfect square)81 = 9 x 9 (it is a perfect square)121 = 11 x 11 (it is a perfect square)The non-perfect square is shown below
198 = 14.07 x 14.07 (14.07 is not an integer, hence 198 is not a perfect square)Thus, all the given numbers are perfect squares except 198
Learn more here: https://brainly.in/question/4881002?tbs_match=3
Which expression is always equivalent to sin x when 0° < x < 90°?
(1) cos (90°- x)
(3) cos (2x)
(2) cos (45° - x)
(4) cos x
Answers
The expression that is always equivalent to sin x when 0° < x < 90° is (1) cos (90° - x). Option 1
To understand why, let's analyze the trigonometric functions involved. In a right triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. Since we are considering angles between 0° and 90°, we can guarantee that the side opposite the angle will always be the shortest side of the triangle, and the hypotenuse will be the longest side.
Now let's examine the expression cos (90° - x). The cosine of an angle is defined as the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. In a right triangle, when we subtract an angle x from 90°, we are left with the complementary angle to x. This means that the remaining angle in the triangle is 90° - x.
Since the side adjacent to the angle 90° - x is the same as the side opposite the angle x, and the hypotenuse is the same, the ratio of the adjacent side to the hypotenuse remains the same. Therefore, cos (90° - x) is equivalent to sin x for angles between 0° and 90°.
On the other hand, options (2) cos (45° - x) and (3) cos (2x) do not always yield the same value as sin x for all angles between 0° and 90°. The expression cos x (option 4) is equivalent to sin (90° - x), not sin x.
Option 1 is correct.
For moresuch questions on equivalent visit:
https://brainly.com/question/2972832
#SPJ8
Please help solve this

Answers
Answer: ∞
Step-by-step explanation: First, find the indefinite integral F (x), and then evaluate F (∞)–F(– ∞).
f(t)= (t-5)^2 - 9 what are the zeros of the function? Smaller T: Larger t: What is the vertex of the parabola?: (__,__)
Answers
Smaller t = 2
Larger t = 5
Step-by-step explanation:
Given:
The given function is.
Find the zeros of the function.
Solution:
Simplify the equation above equation.
Now, we first find the root of the above equation.
Use quadratic formula with .
Put a, b and c value in above equation.
For positive sign
t = 2
For negative sign
t = 5
Put t = 2 in given function.
Put t = 5 in given function.
So, the zeros of the function is t = 2 or 5
Therefore, the smaller value of t = 2 and larger value of t = 5.
Please help and show how you found the answer step by step.
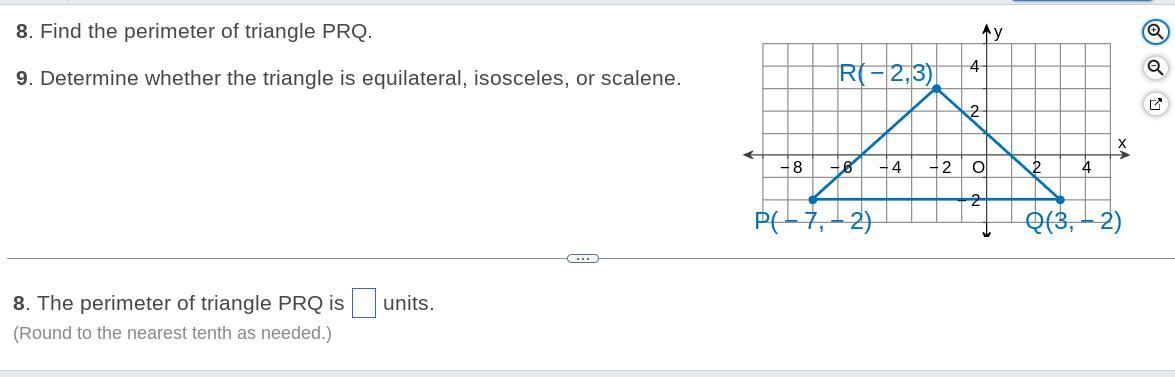
Answers
According to the information, the perimeter of the triangle is ≈ 31.18
How to calculate the perimeter of the triangle?To find the distance between two points, we can use the distance formula:
distance = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Let's label the coordinates as follows:
Point 1: (-2, 3)
Point 2: (3, -2)
Now we can substitute these values into the distance formula:
distance = sqrt((3 - (-2))^2 + (-2 - 3)^2)
distance = sqrt((5)^2 + (-5)^2)
distance = sqrt(25 + 25)
distance = sqrt(50)
distance ≈ 7.07
Therefore, the distance from (-2, 3) to (3, -2) is approximately 7.07 units.
To find the perimeter of the triangle, we need to find the length of all three sides of the triangle and then add them up.
Using the distance formula, we can find the length of the sides:
Side 1: (-2,3) to (3,-2)
d = √[(3 - (-2))^2 + (-2 - 3)^2]
= √[5^2 + (-5)^2]
= √50
= 5√2
Side 2: (3,-2) to (-7,-2)
d = √[(-7 - 3)^2 + (-2 - (-2))^2]
= √[(-10)^2 + 0^2]
= 10
Side 3: (-7,-2) to (-2,3)
d = √[(-2 - (-7))^2 + (3 - (-2))^2]
= √[5^2 + 5^2]
= 5√2
Therefore, the perimeter of the triangle is:
5√2 + 10 + 5√2 = 15√2 + 10 ≈ 31.18 (rounded to two decimal places)
An two of the three sides are equal, so it is an isosceles triangle.
Lean more about isosceles triangle in: https://brainly.com/question/2456591
#SPJ1
5 2/3 + 29/69+6 21/23 what is the sum
Answers
Answer:
To add mixed numbers, we first need to convert them to improper fractions. 5 2/3 = (5 x 3 + 2)/3 = 17/3 6 21/23 = (6 x 23 + 21)/23 = 139/23 Now we add the fractions together: 17/3 + 29/69 + 139/23 To add these fractions, we need to find a common denominator. The smallest common denominator for 3, 69, and 23 is 3 x 69 x 23 = 15087. So we rewrite each fraction with the common denominator: 17/3 x 5039/5039 = 85763/15087 29/69 x 219/219 = 633/15087 139/23 x 657/657 = 9123/15087
Type the correct answer in each box. Functions h and K are inverse functions, and both are defined for all real numbers Using this relationship, what is the value of each function composition?
(h o k) (3)=
(k o h)(-4b) =
Answers
Answer:
(h o k) (3) = 3
(k o h) (-4b) = -4b
Step-by-step explanation:
An inverse function is the opposite of a function. An easy way to find inverse functions is to treat the evaluator like another variable, then solve for the input variable in terms of the evaluator. One property of inverse functions is that when one finds the composition of inverse functions, the result is the input value, no matter the order in which one uses the functions in the combination. This is because all terms in a function and their inverse cancel each other and the result is the input. Thus, when one multiplies two functions that are inverse of each other, no matter the input, the output will always be the input value.
This holds true in this case, it is given that (h) and (k) are inverses. While one is not given the actual function, one knows that the composition of the functions (h) and (k) will result in the input variable. Therefore, even though different numbers are being evaluated in the composition, the output will always be the input.
Determine whether each of the following provides enough information to prove that △SQP ≅ △SQR. Select Yes or No for each statement.
Q is the midpoint of PR.
∠P ≅ ∠R
∠SQP is a right angle, ∠PSQ ≅ ∠RSQ
∠SQP is a right angle, m∠P = 33°, m∠RSQ = 57°
∠P ≅ ∠R, ∠PSQ ≅ ∠RSQ
Answers
For each statement for triangle SQP and SQR, Q is the midpoint of PR: No, ∠P ≅ ∠R: No, ∠PSQ ≅ ∠RSQ: Yes, m∠P = 33°, m∠RSQ = 57°: No, ∠P ≅ ∠R, ∠PSQ ≅ ∠RSQ: Yes.
What is triangle?
A triangle is a geometric shape that consists of three line segments connected end-to-end to form a closed shape. Triangles are one of the basic shapes studied in geometry and are used in a wide range of applications, from construction to computer graphics.
Here are the answers to whether each statement provides enough information to prove that △SQP ≅ △SQR:
Q is the midpoint of PR: No, this information alone is not sufficient to prove the triangles are congruent. We need additional information about the angles or sides.
∠P ≅ ∠R: No, this information alone is not sufficient to prove the triangles are congruent. We need additional information about the sides or other angles.
∠SQP is a right angle, ∠PSQ ≅ ∠RSQ: Yes, this information is sufficient to prove that the triangles are congruent by the angle-angle-side (AAS) congruence criterion.
∠SQP is a right angle, m∠P = 33°, m∠RSQ = 57°: No, this information alone is not sufficient to prove the triangles are congruent. We need additional information about the sides or other angles.
∠P ≅ ∠R, ∠PSQ ≅ ∠RSQ: Yes, this information is sufficient to prove that the triangles are congruent by the angle-angle-angle (AAA) congruence criterion.
To learn more about triangle visit:
https://brainly.com/question/17335144
#SPJ1
Prove that if x and y are rational then their product is also rational. First write a proof on your own and then put the following statements into order to obtain the proof. Put N next to the statements that should not be used in the proof. 1. Then, xy=acbd . 2. Suppose x and y are arbitrary rational numbers. 3. Since a, c are integers, e=ac is also an integer.
Answers
Answer:
Step-by-step explanation:
The aim of this question is to prove that the product of two rationals is rational.
To proof:
If \(\mathbf{x \ and \ y}\) are arbitrary rational numbers.
Thus, going by the definition of rational, there exist integers
a, b, ≠ 0, c, and d ≠ 0 ; \(x = \dfrac{a}{b} \ and \ y = \dfrac{c}{d}\)
Hence, \(xy = (\dfrac{a}{b})(\dfrac{c}{d}) = \dfrac{ac}{bd}\)
Since a and c are integers, then e = ac appears to be an integer as well.
Also, provided that b and d are non-zero integers;
f =bd appears to be a non-zero integer.
Therefore, \(xy = \dfrac{e}{f}\), and going by the definition of rational, xy is rational.
Hence, from the complete question:
The order of the statement is:
7,6,3,5,2,4
The statements that should not be used in the proof are:
1 N
8 N
9 N
10 N
11 N
The blue dot is at what value on the number line?
13
9+

Answers
odd numbers.
From 9 to 11 to 13 to 15 then 17.
So the blue dot is 17.
PLASE HELP !
Which of the following could be the lenghts of the sides for a triangle that is similarto the one shown ? 4 left 9 right 12 down ( no picture) .
A. 12,18, and 26
B. 2,4.5, and 6
C. 10,18, and 24
D. 6,12.5, and 18
Answers
The triangle having lengths 2,4.5, and 6 is similar to the given triangles.
What are similar triangles?Similar triangles are the triangles that look similar to each other but their sizes might not be exactly the same.
Given that, a triangle have side lengths 4 left 9 right 12 down, we need to find the lengths of the similar triangle to it from the given options,
We know that, two triangles to be similar, they should have equal ratios of the corresponding sides,
Therefore,
1) 12,18, and 26
Checking for the ratio,
4 / 12 = 1 /3, 9 / 18 = 1 / 2
Therefore,
The sides are not in equal ratios.
2) 2,4.5, and 6
Checking for the ratio,
4 / 2 = 2, 9 / 4.5 = 2 and 12 / 6 = 2
Since, the sides are in equal ratios.
Therefore, the triangle having lengths 2,4.5, and 6 is similar to the given triangles.
Learn more about similar triangles, click;
https://brainly.com/question/14926756
#SPJ1
Find the orthocenter for the triangles described by each set of vertices. Please help thank you!

Answers
9514 1404 393
Answer:
(4, -1)
Step-by-step explanation:
The orthocenter is the intersection of altitudes. Each altitude is the line through a vertex and perpendicular to the opposite side of the triangle.
It is useful to plot the points on a graph. This shows you segment KM is a horizontal line, so one altitude line is x=4, the vertical line through point L.
The graph also shows you segment KL has a rise of 8 for a run of 2, so a slope of rise/run = 8/2 = 4. Then the altitude perpendicular to that side will have slope -1/4 (the opposite reciprocal of 4), and will go through point M(8, -2). In point-slope form, the equation of the altitude through M can be written ...
y -k = m(x -h) . . . . . . . line with slope m through point (h, k)
y +2 = -1/4(x -8)
We want to find the y-coordinate of the point of intersection of this line with the line x=4. We can substitute x=4 and solve for y.
y +2 = -1/4(4 -8) . . . . . . substitute x=4
y = 1 -2 . . . . . . . . . . simplify and subtract 2
y = -1
The orthocenter for the given triangle has coordinates (4, -1).

The sum of two numbers is 14 and the difference between the numbers is 20. What could one of the numbers be?
Answers
The number will x=17 and y=-3 as the sum of two numbers is 14 and the difference between the numbers is 20.
What is arithmetic operation?The addition, subtraction, multiplication, division, exponentiation, and modulus operations are carried out by the arithmetic operators. One operand is added to the other in addition. On the provided operands, the operator is accustomed to performing mathematical operations like addition, subtraction, multiplication, division, modulus, etc. Examples of arithmetic operators include: 5 + 3 = 8, 5 - 3 = 2, 2 * 4 = 8, etc.
Here,
x+y=14
x-y=20
subtract equation,
2y=-6
y=-3
x+y=14
x-3=14
x=17
The result will be x=17 and y=-3 because the sum of the two numbers is 14 and their difference is 20.
To know more about arithmetic operation,
https://brainly.com/question/28637302?referrer=searchResults
#SPJ13
Find the smallest positive integer that satisfies both of the following equations: = 3 (mod4) and = 5 (mod6)
Answers
Answer:
x=3mod4
Means that when x is divided by 4 it gives an unknown integer and a remainder of 3.
x/4 = Z + 3/4
Z= (x-3)/4
Where Z is the integer
x=5 mod6
x/6 = Y + 5/6
Y = (x-5)/6
Where Y is the integer
Z-Y must be an integer on equal to zero
(x-3)/4 - (x-5)/6
3(x-3)/12 - 2(x-5)/12
(3x-9-2x+10)/12
(x+1)/12
If it is equal to 0
x=-1. But x should be positive
If it is equal to 1
x=11
Hence the smallest possible number is 11
C={-9,-6, -3, 3, 6, 9} by using set building method.
Answers
Answer:
Step-by-step explanation:
In the set-builder notation, the set C that contains the elements {-9, -6, -3, 3, 6, 9} can be written as:
C = {x | x ∈ Z and x ∈ {-9, -6, -3, 3, 6, 9}}
where "x" is a variable, "Z" represents the set of integers, and the expression "x ∈ {-9, -6, -3, 3, 6, 9}" specifies that x can only take on the values of -9, -6, -3, 3, 6, or 9.
Alternatively, we can write it as:
C = {-9, -6, -3, 3, 6, 9}
This notation is used to express a set of elements that have a common property or belong to a specific category, it makes it easy to understand and to read what the set consists of.
