What is the answer of 6xy + (-9xy)
Answers
Answer:
-3xy
Step-by-step explanation:
Answer:
6xy + ( -9xy) = 6xy - 9xy = -3xy
Related Questions
help help HELP!!! PLEASE

Answers
Slope 1/2
y intercept (0,1)
x y
-2 0
0. 1
The student council made a pront of $3,000 on a car wash. If they invest the money at 5% interest
compounded yearly, how much money would they have in four years?
Answers
Answer:
$3375 money would the student council have in four years if they invest $3000 at 5% interest compounded yearly.
Step-by-step explanation:
We are given:
Principal Amount = $3000
Interest Rate r = 5% or 0.05
n=1 (compounded yearly)
Years t= 4
We need to find future value (A)
The formula used is: \(A=P(1+\frac{r}{n})^{nt}\)
Putting values in formula and finding future value A
\(A=P(1+\frac{r}{n})^{nt}\\A=3000(1+\frac{0.05}{1})^{1*4}\\A=3000(1+0.05)^4\\A=3000(1.05)^4\\A=3000(1.215)\\A=3375\)
So, $3375 money would the student council have in four years if they invest $3000 at 5% interest compounded yearly.
Elijah and Riley are playing a board game. Elijah chooses the dragon for his game piece, and Riley chooses the cat for hers.
The dragon is about 1/2inch tall, and the cat is about
7/8 inch tall. The model shows how the heights of the game pieces are related.
\Two bars are shown directly next to each other from left to right. The left bar is labeled How much taller is the cat than the dragon?
Answers
Answer:
3/8
Step-by-step explanation:
The answer would be 3/8 because if you take 7/8 and subtract 1/2 from the height of the cat after finding equivelent denominators you'd get 7/8. hope I helped :)
Answer:
its 3/8
Step-by-step explanation:
Can anyone solve this for me?
\(x^{2}\)+9x-6
x = \(\frac{-1^{2} }{3}\)
Answers
Answer: 9x - 485/81
------------------------------
Simplify
\( \sqrt[4]{ {5}^{4} } \)
4
5
25
625
Answers
Answer:
5
Step-by-step explanation:
\( \sqrt[4]{ {5}^{4} } \\ = ({5}^{4})^{ \frac{1}{4} } \\ = {5}^{ \frac{4}{4} } \\ = 5\)
Answer:
5
Step-by-step explanation:
(Solving Equations Using Square and Cube Roots LC)
Solve y3 = −1.
y = −0.5
y = 0.5
y = −1
y = ±1
Answers
Answer:
Step-by-step explanation:
J Square Roots and Cube Roots To find the square root of a number, you want to find some number that when multiplied by itself gives you the original number. In other words, to find the square root of 25, you want to find the number that when multiplied by itself gives you 25. The square root of 25, then, is 5. The symbol for square root is equation.
1 of 10
Factorise
C2 – 49
1
Answers
Answer:
The factorization of the given expression is \((c - 7)(c+7)\).
Step-by-step explanation:
Consider the provided information.
\(c^2-49\)
Use the formula of the difference of the square in order to factorize the given expression: \(a^2-b^2=(a+b)(a-b)\)
\(c^2-49=c^2 - 7^2\)
\(c^2-49=(c - 7)(c+7)\)
Hence, the factorization of the given expression is \((c - 7)(c+7)\).
6. Prove that if n∈Z and n>2, then zˉ =z n−1 has n+1 solutions.
Answers
As θ ∈ [0, 2π), we have another solution at θ = 2π. Thus, this gives n solutions.
Given: n ∈ Z and n > 2, prove that z¯ = zn−1 has n+1 solutions.
Proof:Let z = r(cos θ + i sin θ) be the polar form of z, where r > 0 and θ ∈ [0, 2π).Then, zn = rⁿ(cos nθ + i sin nθ)and, z¯ = rⁿ(cos nθ - i sin nθ)
Now, z¯ = zn−1 will imply that: rⁿ(cos nθ - i sin nθ) = rⁿ(cos (n-1)θ + i sin (n-1)θ).
As the moduli on both sides are the same, it follows that cos nθ = cos (n-1)θ and sin nθ = -sin (n-1)θ.
Thus, 2cos(θ/2)sin[(n-1)θ + θ/2] = 0 or cos(θ/2)sin[(n-1)θ + θ/2] = 0.
As n > 2, we know that n - 1 ≥ 1.
Thus, there are two cases:
Case 1: θ/2 = kπ, where k ∈ Z. This gives n solutions.
Case 2: sin[(n-1)θ + θ/2] = 0. This gives (n-1) solutions.
However,as [0, 2], we have a different answer at [2:2].
Thus, this gives n solutions.∴ The total number of solutions is n + 1.
learn more about solution from given link
https://brainly.com/question/27371101
#SPJ11
find an equation of the tangent line to the graph of f(x) = xe^−x at its inflection point.
Answers
Answer:
y = (4 -x)e^-2
Step-by-step explanation:
You want an equation of the tangent line to the graph of f(x) = xe^−x at its inflection point.
Inflection pointThe inflection point on a curve is the point where the second derivative is zero, where the curve changes from being concave downward to concave upward, or vice versa.
We can use the product rule to differentiate f(x):
(uv)' = u'v +uv'
f'(x) = 1·e^-x +x·(-1)(e^-x) = (e^-x)(1 -x)
Then the second derivative is ...
f''(x) = (-e^-x)(1 -x) +(e^-x)(-1) = (e^-x)(x -2)
The second derivative is zero where one of its factors is zero. e^-x is never zero, so we have ...
(x -2) = 0 ⇒ x = 2
The point of inflection occurs at x = 2.
Point-slope equationThe point-slope equation of the line with slope m through point (h, k) is ...
y -k = m(x -h)
For this problem, we have ...
m = f'(2) = (e^-2)(1 -(2)) = -e^-2
(h, k) = (2, f(2)) = (2, 2e^-2)
So, the equation of the tangent line is ...
y -2e^-2 = -e^-2(x -2)
In slope-intercept form, this is ...
y = (-e^-2)x +4e^-2
__
Additional comment
We can rearrange the equation to ...
y = (4 -x)e^-2
Usually a tangent line touches the graph, but does not cross it. The tangent at the point of inflection necessarily crosses the graph.

Jorge solves the equation 4 x minus (x + 2) + 6 = 2 (3 x + 8) using the steps below. Step 1: 4 x minus x + 2 + 6 = 6 x + 16 Step 2: 3 x + 8 = 6 x + 16 Step 3: 8 minus 16 = 6 x minus 3 x Step 4: Negative 8 = 3 x Step 5: Negative StartFraction 8 Over 3 EndFraction = x BRAINLISEST
Answers
Answer:
The solution of the given equation is x = -4
Step-by-step explanation:
Explanation:-
Given expression 4 x - (x +2) +6 = 2 (3 x+8)
Step(i):-
4 x - (x +2) +6 = 2 (3 x+8)
4 x - x -2 + 6 = 6 x + 16
step(ii):-
3 x + 4 = 6 x + 16
subtracting '4' on both sides , we get
3 x + 4 - 4 = 6 x + 16 - 4
3 x = 6 x + 12
Step(iii):-
Subtracting '6x' on both sides , we get
3 x - 6 x = 6 x - 6 x + 12
- 3 x = 12
Step(iv):-
Dividing '-3' on both sides , we get
\(\frac{-3x}{-3} = \frac{12}{-3}\)
x = - 4
Final answer:-
The solution of the given equation is x = -4
Verification:-
4 x - (x +2) +6 = 2 (3 x+8)
put x = -4
4 ( -4) - ( - 4 +2) +6 = 2 (3(-4)+8)
-16+2+6 = 2 (-12+8)
-8 = -8
Both are equal
Answer:
For everyone on Edge, It's A: He distributed incorrectly.
Step-by-step explanation:
he didn't distribute at all so
im pretty sure.
The diameter of a circle is 8 mm. What is the circumference of the circle?
Answers
Answer:
C=22÷7×8
=3.14×8
=25.12
what is 69 divided by 1,656
Answers
Answer:
60 divide by 1656 is 0.0416
Step-by-step explanation:
Determine the Fourier series representation for the 2n periodic signal defined below:
f(x) x 0
π, π
Answers
The Fourier series representation of the 2π periodic signal f(x) = x for 0 < x < π is (π/4) + Σ[(-1/n) \((-1)^n\) sin(nω₀x)].
To determine the Fourier series representation of the periodic signal f(x) = x for 0 < x < π with a period of 2π, we can use the following steps:
Determine the coefficients a₀, aₙ, and bₙ:
a₀ = (1/π) ∫[0,π] f(x) dx
= (1/π) ∫[0,π] x dx
= (1/π) [x²/2] ∣ [0,π]
= (1/π) [(π²/2) - (0²/2)]
= π/2
aₙ = (1/π) ∫[0,π] f(x) cos(nω₀x) dx
= (1/π) ∫[0,π] x cos(nω₀x) dx
bₙ = (1/π) ∫[0,π] f(x) sin(nω₀x) dx
= (1/π) ∫[0,π] x sin(nω₀x) dx
Simplify and evaluate the integrals:
For aₙ:
aₙ = (1/π) ∫[0,π] x cos(nω₀x) dx
For bₙ:
bₙ = (1/π) ∫[0,π] x sin(nω₀x) dx
Write the Fourier series representation:
f(x) = a₀/2 + Σ[aₙcos(nω₀x) + bₙsin(nω₀x)]
where Σ represents the summation from n = 1 to ∞.
To evaluate the integrals for aₙ and bₙ and determine the specific values of the coefficients, let's calculate them step by step:
For aₙ:
aₙ = (1/π) ∫[0,π] x cos(nω₀x) dx
Using integration by parts, we have:
u = x (derivative = 1)
dv = cos(nω₀x) dx (integral = (1/nω₀) sin(nω₀x))
Applying the integration by parts formula, we get:
∫ u dv = uv - ∫ v du
Plugging in the values, we have:
aₙ = (1/π) [x (1/nω₀) sin(nω₀x) - ∫ (1/nω₀) sin(nω₀x) dx]
= (1/π) [x (1/nω₀) sin(nω₀x) + (1/nω₀)² cos(nω₀x)] ∣ [0,π]
= (1/π) [(π/nω₀) sin(nω₀π) + (1/nω₀)² cos(nω₀π) - (0/nω₀) sin(nω₀(0)) - (1/nω₀)² cos(nω₀(0))]
= (1/π) [(π/nω₀) sin(nπ) + (1/nω₀)² cos(nπ) - 0 - (1/nω₀)² cos(0)]
= (1/π) [(π/nω₀) sin(nπ) + (1/nω₀)² - (1/nω₀)²]
= (1/π) [(π/nω₀) sin(nπ)]
= (1/n) sin(nπ)
= 0 (since sin(nπ) = 0 for n ≠ 0)
For bₙ:
bₙ = (1/π) ∫[0,π] x sin(nω₀x) dx
Using integration by parts, we have:
u = x (derivative = 1)
dv = sin(nω₀x) dx (integral = (-1/nω₀) cos(nω₀x))
Applying the integration by parts formula, we get:
∫ u dv = uv - ∫ v du
Plugging in the values, we have:
bₙ = (1/π) [x (-1/nω₀) cos(nω₀x) - ∫ (-1/nω₀) cos(nω₀x) dx]
= (1/π) [-x (1/nω₀) cos(nω₀x) + (1/nω₀)² sin(nω₀x)] ∣ [0,π]
= (1/π) [-π (1/nω₀) cos(nω₀π) + (1/nω₀)² sin(nω₀π) - (0 (1/nω₀) cos(nω₀(0)) - (1/nω₀)² sin(nω₀(0)))]
= (1/π) [-π (1/nω₀) cos(nπ) + (1/nω₀)² sin(nπ)]
= (1/π) [-π (1/nω₀) \((-1)^n\) + 0]
= (-1/n) \((-1)^n\)
Now, we can write the complete Fourier series representation:
f(x) = a₀/2 + Σ[aₙcos(nω₀x) + bₙsin(nω₀x)]
Since a₀ = π/2 and aₙ = 0 for n ≠ 0, and bₙ = (-1/n) \((-1)^n\), the Fourier series representation becomes:
f(x) = (π/4) + Σ[(-1/n) \((-1)^n\) sin(nω₀x)]
where Σ represents the summation from n = 1 to ∞.
This is the complete Fourier series representation of the given 2π periodic signal f(x) = x for 0 < x < π.
Learn more about the Fourier series at
https://brainly.com/question/31046635
#SPJ4
The question is -
Determine the Fourier series representation for the 2n periodic signal defined below:
f(x) = x, 0 < x < π
1) according a survey found 58% of adults enjoy superhero movies. if eight adults are randomly selected, find the probability that a minimum of seven adults enjoy superhero movies.
Answers
The probability that a minimum of seven adults enjoy superhero movies is P(X ≥ 7) = P(X = 7) + P(X = 8)
You can calculate the specific values using the formulas and then sum them up to find the probability that a minimum of seven adults enjoy superhero movies out of the random sample of eight adults.
To find the probability that a minimum of seven adults enjoy superhero movies out of a random sample of eight adults, we need to calculate the probability of different scenarios: exactly 7 adults, exactly 8 adults, and add them together.
First, let's calculate the probability that exactly 7 adults enjoy superhero movies. We can use the binomial probability formula:
P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)
Where:
P(X = k) is the probability of getting exactly k successes,
C(n, k) is the combination formula (n choose k),
p is the probability of success (58% or 0.58 in decimal form),
n is the number of trials (8 in this case), and
k is the number of successes (7).
Using the formula, we can calculate:
P(X = 7) = C(8, 7) * 0.58^7 * (1 - 0.58)^(8 - 7)
Similarly, the probability that exactly 8 adults enjoy superhero movies is:
P(X = 8) = C(8, 8) * 0.58^8 * (1 - 0.58)^(8 - 8)
To find the probability of a minimum of seven adults enjoying superhero movies, we add these two probabilities together:
P(X ≥ 7) = P(X = 7) + P(X = 8)
Know more about probability here;
https://brainly.com/question/31828911
#SPJ11
Question 13 of 20 :
Select the best answer for the question.
13. Find the distance between the points (-1/2,-8) and (-1/2,-2).
O A. 6
O B.1/2
O C. 10
O D. 8
Mark for review (Will be highlighted on the review page)
<< Previous Question
Next Question >>
Answers
Answer:
a) 6
Step-by-step explanation:
distance formula = the sq rt of the (difference of the y-values)² + (difference of the x-values)²
= \(\sqrt{(-6^2) + (0^2)}\)
= \(\sqrt{36}\)
= 6
if you are given one or more of the first few terms of a sequence, and all other terms of the sequence are defined using previous terms, then the sequence is said to be defined
Answers
If a sequence is defined using previous terms, it is known as a recursively defined sequence.
This type of sequence relies on the previous terms to determine the next term in the sequence. The number of terms that are required to define a recursively defined sequence varies depending on the specific sequence. However, if the first few terms of the sequence are given, it can help determine the pattern and the formula used to generate subsequent terms. A good understanding of recursive sequences can be helpful in many areas, including computer programming, mathematics, and finance. A sequence that is defined using its initial terms and a rule relating its subsequent terms to the previous ones is called a recursively defined sequence. In such sequences, each term's value depends on one or more earlier terms. The first few terms serve as the basis, and the recursive formula generates the remaining terms. This approach allows us to find any term in the sequence based on previous ones, ensuring a consistent pattern and progression.
To know more about sequence visit:
https://brainly.com/question/28615767
#SPJ11
consider the quadratic function y equals short dash x squared plus 6 x minus 5. what do we know about the graph of this quadratic equation, based on its formula?
Answers
Based on the formula of the quadratic function y=-x^2+6x-5, we know that its graph is a downward-facing parabola that opens wide, with a vertex at (3,-14), and an axis of symmetry at x=3.
Based on the formula of the quadratic function y=-x^2+6x-5, we can determine several properties of its graph, including its shape, vertex, and axis of symmetry.
First, the negative coefficient of the x-squared term (-1) tells us that the graph will be a downward-facing parabola. The leading coefficient also tells us whether the parabola is narrow or wide. Since the coefficient is -1, the parabola will be wide.
Next, we can find the vertex using the formula:
Vertex = (-b/2a, f(-b/2a))
where a is the coefficient of the x-squared term, b is the coefficient of the x term, and f(x) is the quadratic function. Plugging in the values for our function, we get:
Vertex = (-b/2a, f(-b/2a))
= (-6/(2*-1), f(6/(2*-1)))
= (3, -14)
So the vertex of the parabola is at the point (3,-14).
Finally, we know that the axis of symmetry is a vertical line passing through the vertex. In this case, it is the line x=3.
Know more about quadratic function here;
https://brainly.com/question/18958913
#SPJ11
What is the least common denominator of 5/8 and 1/6
Answers
Answer:
24
Step-by-step explanation:
Equivalent fractions with the LCD
5/8 = 15/24
1/6 = 4/24
Help
Help me simplify this equation
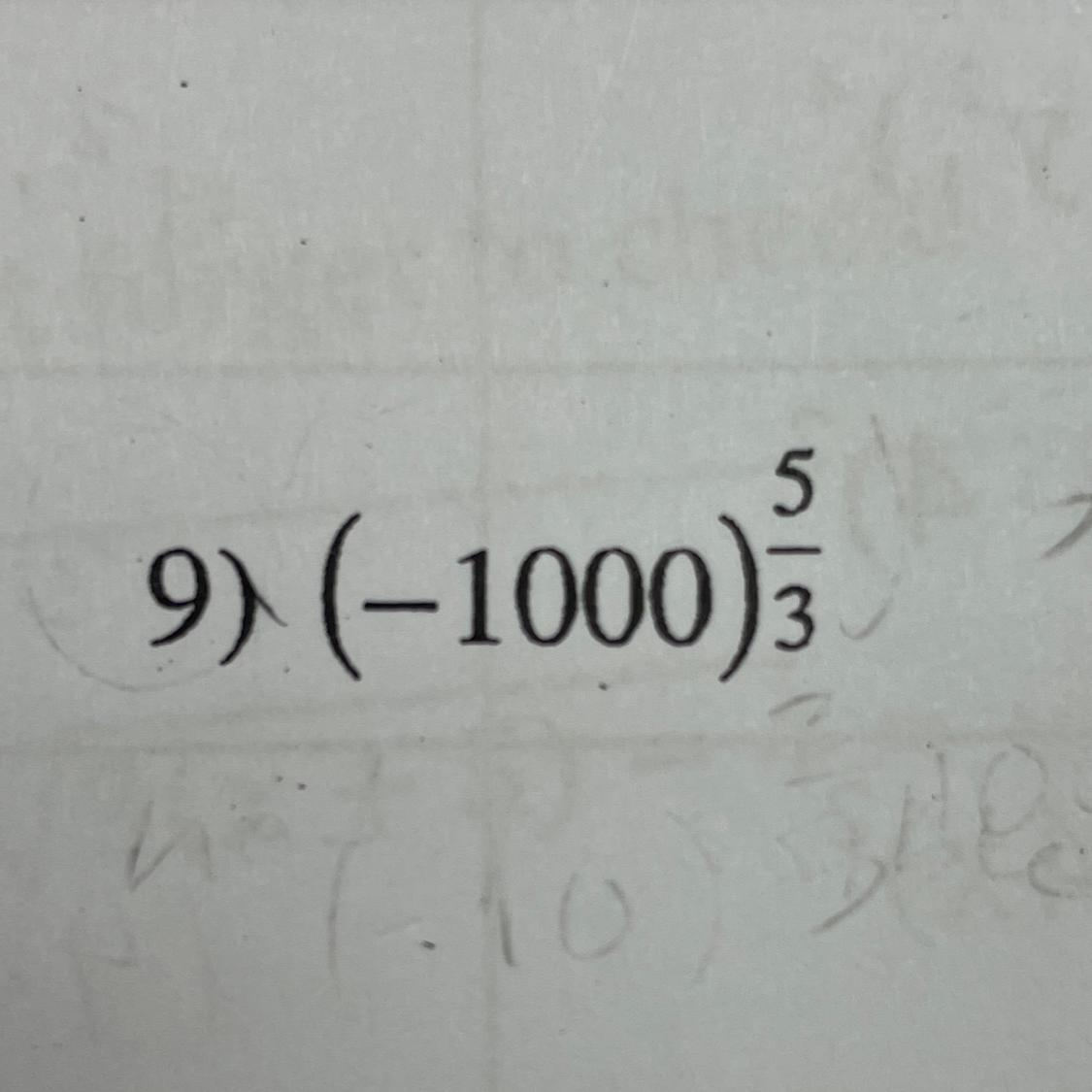
Answers
Answer:
-100000
Step-by-step explanation:
\((-1000)^{5/3} \\ \\ =(\sqrt[3]{-1000})^5 \\ \\ =(-10)^5 \\ \\ =-100000\)
Write a proof sequence for each of the following assertions. Justify each step.p→¬qr → (p ∧ q) }⇒ ¬r
Answers
To prove the assertion (p→¬q), (r → (p ∧ q)) ⇒ ¬r using a proof sequence. Here's the step-by-step justification:
1. (p→¬q) - Given as a premise
2. (r → (p ∧ q)) - Given as a premise
3. Assume r - Assumption for a proof by contradiction
4. (p ∧ q) - From 2 and 3, using Modus Ponens
5. p - From 4, using the Simplification rule (Conjunction elimination)
6. ¬q - From 1 and 5, using Modus Ponens
7. q - From 4, using the Simplification rule (Conjunction elimination)
8. (¬q ∧ q) - From 6 and 7, using the Conjunction Introduction rule
9. ¬r - From 3 and 8, using a proof by contradiction (Reductio ad absurdum)
The proof sequence shows that, given the premises (p→¬q) and (r → (p ∧ q)), the assertion ¬r can be proven.
To learn more about proof sequence visit:
brainly.com/question/30589255
#SPJ11
plz plz answer this i'll give 11 points

Answers
Answer:
A =bh
Step-by-step explanation:
2 1/2 times 5 1/4 = 13.125
The formula to find the area of a triangle is A = { bh where b=base and h=height. Rearrange the
equation to highlight b, the base of the triangle, in terms of the area and height.
Answers
Answer:
A=B+H
Step-by-step explanation:
I rearange the letters and also I put a plus singe
Someone plz help giving brainliest

Answers
Answer:
Its C.
Step-by-step explanation:
I had this and its C. trust me
im really confused on this please help if you can

Answers
Answer:
A. 2\(\frac{1}{2}\)
Step-by-step explanation:
You have to replace x with one of the values in the set. You have to find the one that works.
3\(\frac{1}{2}\)x = 8\(\frac{3}{4}\)
8\(\frac{3}{4}\) ÷ 3\(\frac{1}{2}\) = x
8\(\frac{3}{4}\) ÷ 3\(\frac{1}{2}\) = 2\(\frac{1}{2}\)
Hope this helps :)
finding the difference

Answers
Answer:
\(-2.5a^2+1.3a-3\)
Step-by-step explanation:
What does an extension ladder's size classification indicate?
Select one:
a.The minimum reach when placed at the appropriate climbing angle
b.The ladder's length when the fly section is not extended
c.The maximum building height against which the ladder can be raised
d.The full length to which it can be extended
Answers
The correct answer is (D) The full length to which it can be extended.
The size classification of an extension ladder indicates the full length to which it can be extended.
An extension ladder's size classification indicates the total length the ladder can reach when its fly section is fully extended.
This helps users determine if the ladder will be long enough for their specific needs when working at height.
Know more about the length here:
https://brainly.com/question/2217700
#SPJ11
Put the following equation of a line into slope-intercept form, simplifying all fractions.
6x+2y=-8
Answers
Answer:
y = 3x - 5
Step-by-step explanation
Answer:
Y = 3x - 5
Step-by-step explanation:
6x - 2y = 10
-2y = -6x + 10
y = 3x - 5
The volume of a box 4in wide 2in high and 5in long is
Answers
Answer:
40 cubic inches
Step-by-step explanation:
The Formula for Volume: Length x Width x Height (L x W x H)
4 times 2 times 5 = 40
Last questionnn! :))))

Answers
Answer:
Step-by-step explanation:
Angle 1 and Angle 2 add up to 90 degrees (a right angle).
Angle 1 is (x-5) and Angle 2 is 4x.
So let's add those up and set them equal to 90.
(x-5) + 4x = 90
Now solve for x.
5x - 5 = 90
5x = 95
x = 19
Substitute x = 19 back into the provided equations for Angle 1 and Angle 2.
Angle 1 = x-5 = 19-5 = 14 degrees.
Angle 2 = 4x = 4*19 = 76 degrees.
Now do a check - - - angle 1 + angle 2 should equal 90!
14 + 76 = 90 degrees.
How do you find the coefficient of x7 in (1+x)11?
Answers
The coefficient of x^7 in (1+x)^11 can be found by using binomial theorem and the result is 330.
To find the coefficient of x^7 in (1+x)^11, we can use the binomial theorem, which states that:
(1+x)^n = C(n,0) + C(n,1)x + C(n,2)x^2 + ... + C(n,n)x^n
where C(n,k) denotes the binomial coefficient "n choose k", which is the number of ways to choose k items from a set of n distinct items.
So in this case, we want to find the coefficient of x^7, which corresponds to the term C(11,7)x^7. We can use the formula for binomial coefficients:
C(n,k) = n! / (k!(n-k)!)
to compute the value of C(11,7):
C(11,7) = 11! / (7!4!) = (11x10x9x8) / (4x3x2x1) = 330
Learn more about binomial theorem here
brainly.com/question/13873595
#SPJ4
The given question is incomplete, the complete question is:
How do you find the coefficient of x^7 in (1+x)^11?