What is solution to this system of equations? x + 4y = 12 and x = 0
PLSSS hurry
Answers
Answer:
x=0 and y=3
Step-by-step explanation:
If x=0, then we can just plug that value into the other equation and solve for y:
x+4y=12
0+4y=12
4y=12
y=3
Therefore, the solution to the system of equations is x=0 and y=3
Answer:
y = 3
Step-by-step explanation:
It is given that x = 0,
So by substituting it in the equation x + 4y = 12
=> 0 + 4y = 12
=> 4y = 12 - 0 (by transposing)
=> 4y = 12
=> y = 12/4 = 3
Hope you understood!!
Related Questions
solve. minimize: w=35y1 72y2 65y3 subject to: with: write only the exact value for . do not round. if necessary, write as a fraction o
Answers
The solution to the equation is y₂ = -13.51.
To find the exact value of y₂ without rounding, we will use the method of corner points. This method involves finding the corner points of the feasible region and evaluating the objective function at each corner point to determine the optimal solution.
Step 1: Setting up the inequalities:
Let's rewrite the constraints with variables in terms of a fraction:
Constraint 1: 5y₁ + 9y₂ + 4y₃ < 15 ... (1)
Constraint 2: 5y₁ + 18y₂ + 2y₃ > 8 ... (2)
Step 2: Solving for y₂:
To solve for y₂, we will express y₂ in terms of the other variables in the constraints.
From constraint (1), we have:
5y₁ + 9y₂ + 4y₃ < 15
9y₂ < 15 - 5y₁ - 4y₃
y₂ < (15 - 5y₁ - 4y₃)/9
From constraint (2), we have:
5y₁ + 18y₂ + 2y₃ > 8
18y₂ > 8 - 5y₁ - 2y₃
y₂ > (8 - 5y₁ - 2y₃)/18
Step 3: Analyzing the constraints:
Now we have the inequalities for y₂ in terms of y₁, y₃, and constants. Let's examine the conditions to satisfy the constraints:
y₂ > (8 - 5y₁ - 2y₃)/18 ... (3)
y₂ < (15 - 5y₁ - 4y₃)/9 ... (4)
Considering the constraints y₁ > 0, y₃ > 0, and y₂ > 0, we need to find the range of values for y₁ and y₃ that satisfy these inequalities.
Analyzing the inequalities:
Let's examine the intervals for y₁ and y₃ that satisfy the constraints:
From inequality (3):
y₂ > (8 - 5y₁ - 2y₃)/18
For y₁ > 0 and y₃ > 0, the numerator 8 - 5y₁ - 2y₃ should be positive to maintain y₂ > 0.
Simplifying the numerator:
8 - 5y₁ - 2y₃ > 0
8 > 5y₁ + 2y₃
This implies that 5y₁ + 2y₃ < 8.
From inequality (4):
y₂ < (15 - 5y₁ - 4y₃)/9
For y₁ > 0 and y₃ > 0, the numerator 15 - 5y₁ - 4y₃ should be positive to maintain y₂ > 0.
Simplifying the numerator:
15 - 5y₁ - 4y₃ > 0
15 > 5y₁ + 4y₃
This implies that 5y₁ + 4y₃ < 15.
Step 5: Finding the corner points:
To find the corner points, we need to determine the intersection of the lines 5y₁ + 2y₃ = 8 and 5y₁ + 4y₃ = 15.
Solving the system of equations:
5y₁ + 2y₃ = 8 ... (5)
5y₁ + 4y₃ = 15 ... (6)
Multiplying equation (5) by 2, we get:
10y₁ + 4y₃ = 16 ... (7)
Subtracting equation (6) from equation (7):
(10y₁ + 4y₃) - (5y₁ + 4y₃) = 16 - 15
5y₁ = 1
Dividing both sides by 5:
y₁ = 1/5
Substituting y₁ = 1/5 into equation (5):
5(1/5) + 2y₃ = 8
1 + 2y₃ = 8
2y₃ = 8 - 1
2y₃ = 7
y₃ = 7/2
Therefore, one corner point is (y₁, y₂, y₃) = (1/5, ?, 7/2).
Step 6: Evaluating the objective function:
Now, let's evaluate the objective function at the corner point (1/5, ?, 7/2) to find the value of y₂.
Substituting the corner point into the objective function:
w = 35y₁ + 72y₂ + 65y₃
w = 35(1/5) + 72y₂ + 65(7/2)
w = 7 + 72y₂ + 2275/2
w = 7 + 72y₂ + 1137.5
w = 1144.5 + 72y₂
172 = 1144.5 + 72y₂
Let's start by subtracting 1144.5 from both sides of the equation:
172 - 1144.5 = 1144.5 + 72y₂ - 1144.5
This simplifies to:
-972.5 = 72y₂
To isolate y₂, we can divide both sides of the equation by 72:
-972.5 / 72 = 72y₂ / 72
Simplifying further:
-13.51 = y₂
To know more about fraction here
https://brainly.com/question/10354322
#SPJ4
Complete Question:
Solve. Minimize: w = 35y₁ + 72y₂ +65y₃
Subject to: 5y₁ +9y₂ + 4y₃ < 15
5y₁ + 18y₂ + 2y₃ > 8
With: y₁ > 0; y₂ > 0; y₃ > 0
Write only the exact value for y₂.
Do not round. If necessary, write as a fraction or improper fraction. Show your work on separate paper.
Hi I need help with this question, please and thank you

Answers
1) Let's rewrite it into the z=a +bi form.
2) So we can write out the following noticing that i² =-1 as well as √-1=i
\(\begin{gathered} \sqrt[]{-1176}=\sqrt[]{-1}\cdot\sqrt[]{1176} \\ Factoring \\ \sqrt[]{-1}\cdot14\sqrt[]{6} \\ i\cdot14\sqrt[]{6} \\ 14\sqrt[]{6}i \end{gathered}\)Note that in this number the real part "a" is equal to 0.
what would the distance between the ordered pairs (-2,3) and (4,-6) be?
Answers
Answer: 5.099
Step-by-step explanation:
Which of the following types of graph is the best kind to use for analyzing how two variables are related?
Answers
Scatter plot is best for analyzing relationship between two variables.
What is scatter ?
In statistics and data visualization, a scatter plot (also called a scatter graph or scatter chart) is a type of graph used to display the relationship between two sets of data. It is a two-dimensional plot that uses Cartesian coordinates to display values for typically two variables for a set of data.
A scatter plot is a graph that uses dots to represent values for two numeric variables. The position of each dot on the horizontal and vertical axis indicates values for an individual data point. Scatter plots are a useful tool for visualizing the relationship between two variables, such as how changes in one variable may be associated with changes in another variable.
Scatter plots can show the following types of relationships:
Positive correlation: as one variable increases, the other variable increases.
Negative correlation: as one variable increases, the other variable decreases.
No correlation: there is no relationship between the two variables.
Non-linear relationship: the relationship between the two variables is not linear.
Scatter plot is best for analyzing relationship between two variables.
Complete Question: Which of the following types of graph is the best kind to use for analyzing how two variables are related?
Line Graphs, Bar Graphs, Pie Charts, Scatter Plots
To learn more about scatter visit : brainly.com/question/13984412
#SPJ4
Use <,>,or = to solve the inequality below
8/10 and 5/10 (fraction s please explain as easy as possible)
Answers
hi
A fraction has two parts :
- numerator ( number on the top of fraction bar )
- and denominator ( number under the fraction bar )
To compare two fractions, they must have the same denominator.
When it is the case, you check for numerator.
Then, you just ask the same question you would do, as you would with two numbers.
Now what do we have here ? 8/10 and 5/10
As 10 is denominator for both , let compare numerator. we have 8 and 5
well, we both know that 8 ≥ 5 , so 8/10 ≥ 5/10
HELPP YALL! I WILL MARK BRAINIEST!! LOOK AT THE PICTURE!!

Answers
I know because I was good at this when I was a freshman
If 63 % of persons like banana while 76 % like apples, what can be said about % of persons who like both banana and apples? Each person eats at least one fruit.
a. 39%
b. 41%
c. 43%
d. 45%
Answers
Each person eats at least one fruit. Hence 39% of people eat both orange and apple using the probability.
Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics. From the given data
n(O)=0.63
n(A)=0.76
n(A∪O)=1 as every person eats at least one fruit
n(A∪O)=n(A)+n(O)−n(A∩B)
1=0.63+0.76−n(A∩B)
n(A∩B)=1.39−1
n(A∩B)=0.39
A∩B=0.39×100=39
Hence 39% of people eat both orange and apple
Learn more about probability here :
https://brainly.com/question/30034780
#SPJ4
Express the confidence interval 0.039 < p < 0.479 in the form of (p) hat ± E.
Answers
The confidence interval 0.039 < p < 0.479 in the form of (p) hat ± E is 0.259 ± 0.22.
(p) is given by the sum of confidence divided by 2
(p) hat = sum of confidence interval / 2
The confidence interval is 0.039 < p < 0.479
(p) hat = ( 0.039 + 0.479 ) / 2
(p) hat = 0.518 / 2
(p) hat = 0.259
E = margin of error
The margin of error is the difference in confidence divided by 2
E = Difference of confidence interval / 2
E = (0.479 - 0.039) / 2
E = 0.44 / 2
E = 0.22
(p) hat ± E = 0.259 ± 0.22
Hence the confidence interval 0.039 < p < 0.479 in the form of (p) hat ± E is 0.259 ± 0.22.
To know more about the confidence of interval click here :
https://brainly.com/question/29680703
#SPJ4
What is the area of a sector with a central angle of 144° and a radius of 11 cm?
Use 3.14 for π and round your final answer to the nearest hundredth.
Enter your answer as a decimal in the box.
Answers
Rounding to the nearest hundredth, the area of the sector is approximately 152.30 cm².
To find the area of a sector, you can use the formula:
\(Area = (\theta /360) \times \pi \times r^2\)
where θ is the central angle and r is the radius.
Plugging in the given values:
θ = 144°
r = 11 cm
π = 3.14
\(Area = (144/360) \times 3.14 \times 11^2\)
Simplifying:
\(Area = (0.4) \times 3.14 \times 121\)
\(Area = 48.4 \times 3.14\)
\(Area = 152.296 cm^2.\)
For similar question on area.
https://brainly.com/question/26870235
#SPJ11
WY bisects ZVWX. If mZVWX = 161°, what is the mZYWX?
Answers
Answer:
No estoy seguro, intenta preguntarle a tu profesor
Step-by-step explanation:
A survey participant is randomly selected. Let S be the event that the participant prefers soccer and let T be the event that the participant prefers a T-shirt. What is the value of P(S and T)
Answers
Answer:
C. 0.26
Step-by-step explanation:
Help needed ASAP will give brainliest and 5 STAR RATE (not a real test)
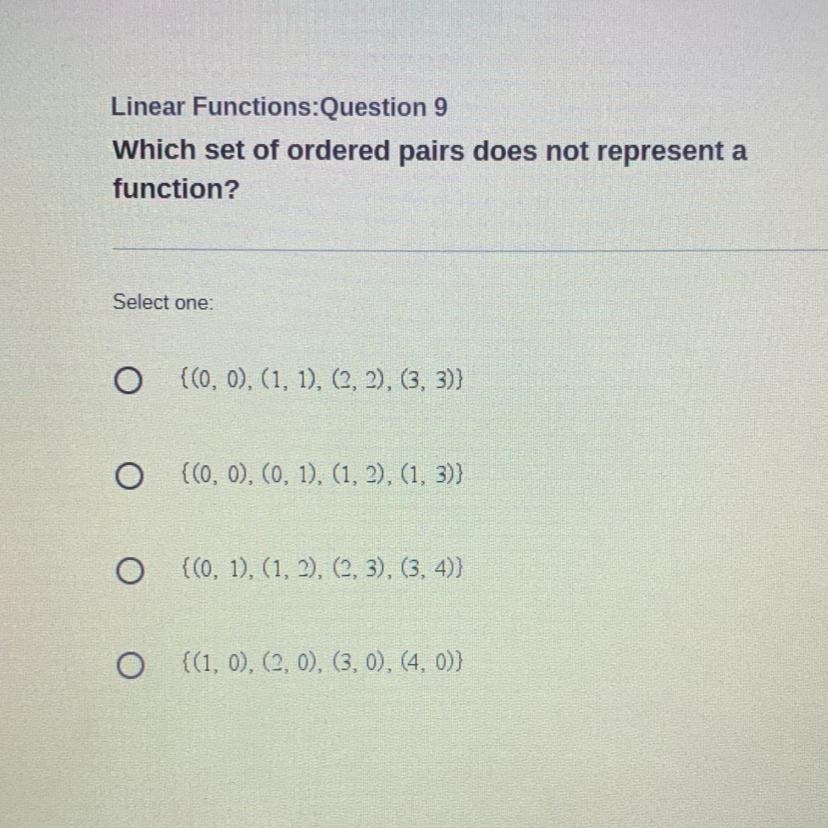
Answers
Answer:
(0,0), (0,1), (1,2), (1,3)
Step-by-step explanation:
To determine what makes ordered pairs a function, we have to make sure each input (x) goes to exactly one output (y).
The reason this is the answer is that each input doesn't have exactly one output. (0 goes to 0 and 1. 1 goes to 2 and 3).
Adam would like to build a deck thatbis 60,feet long by 8 feet hiw much wood would he need
Answers
Answer:
136 ft of woods
Step-by-step explanation:
1. Let us assume that we are solving for the frame of the deck alone
2. And also from the given parameters the deck has a rectangular shape
we know that the total amount of woods to be used is same as the perimeter of the rectangle.
Given that
length l= 60 ft
width w= 8 ft
The formula for the perimeter of a rectangle is given as
Perimeter= 2l+2w
perimeter= 2*60+ 2*8
perimeter= 120+16
perimeter= 136 ft
Hence in other to construct the frame of the deck Adam needs a total of 136 ft of woods
suppose that 19% of people own dogs. if you pick two people at random, what is the probability that they both own a dog?
Answers
The probability that both randomly selected people own a dog is approximately 0.0361, or 3.61%.
To find the probability that both randomly selected people own a dog, we need to multiply the probabilities of each event occurring.
Given that 19% of people own dogs, the probability that a randomly selected person owns a dog is 0.19.
Since we're selecting two people independently, the probability that both of them own a dog can be calculated by multiplying the probabilities:
P(both own a dog) = P(owning a dog for person 1) * P(owning a dog for person 2)
P(both own a dog) = 0.19 * 0.19 = 0.0361
Know more about probability here:
https://brainly.com/question/32004014
#SPJ11
3. Evaluate the following: (a) \( \int e^{\sqrt{x}} d x \) (b) \( \int_{-\infty}^{0} x e^{-x} d x \)
Answers
The value of the integral after evaluating them is given by
a. ∫\(e^\sqrt{x}\) dx is equal to 2√x × \(e^\sqrt{x}\) - 2\(e^\sqrt{x}\) + C.
b. ∫ [-∞, 0] x\(e^{-x\) dx is equal to -x\(e^{-x\) - \(e^{-x\) + C.
a. To evaluate the integral ∫\(e^\sqrt{x}\)dx, we can use a substitution.
Let's substitute u = √x.
Then, differentiating both sides with respect to x,
we have du/dx = 1 / (2√x).
Solving for dx, we get dx = 2√x du.
Substituting these values into the integral, we have,
∫\(e^\sqrt{x}\) dx
= ∫\(e^u\) × 2√x du
= 2∫\(e^u\) × √x du.
Now, express the integral in terms of u only.
Since u = √x, we can rewrite √x as u,
∫\(e^\sqrt{x}\) dx = 2∫\(e^u\) × u du.
This integral can be evaluated using integration by parts.
Let's differentiate u and integrate \(e^u\) to apply the integration by parts formula,
d/dx (u)
= d/du (u) × du/dx
= 1 × 1 / (2√x)
= 1 / (2√x),
∫\(e^u\) du = \(e^u\)
Applying the integration by parts formula, we have,
∫\(e^\sqrt{x}\) dx
= 2 × ∫\(e^u\) × u du
= 2 × (u × \(e^u\) - ∫\(e^u\) × du)
= 2u × \(e^u\) - 2∫\(e^u\)du
= 2u × \(e^u\) - 2× \(e^u\) + C,
where C is the constant of integration.
Substituting u = √x back into the expression, we get the final result:
∫\(e^\sqrt{x}\) dx = 2√x × \(e^\sqrt{x}\) - 2\(e^\sqrt{x}\) + C.
b. To evaluate the integral ∫ [-∞, 0] x\(e^{-x\) dx, we can use integration by parts.
Let's choose u = x and dv = \(e^{-x\)dx.
Then, differentiate u and integrate dv,
du = dx,
v = ∫\(e^{-x\) dx
= -\(e^{-x\)
Using the integration by parts formula ∫u dv = uv - ∫v du, we have,
∫x\(e^{-x\) dx
= uv - ∫v du
= x × (-\(e^{-x\)) - ∫(-\(e^{-x\)) dx
= -x\(e^{-x\) + ∫\(e^{-x\) dx.
The integral ∫\(e^{-x\) dx is simply the negative of \(e^{-x\) so we have,
∫x\(e^{-x\) dx = -x\(e^{-x\) - \(e^{-x\) + C,
where C is the constant of integration.
Therefore, the value of the integral a. ∫\(e^\sqrt{x}\) dx = 2√x × \(e^\sqrt{x}\) - 2\(e^\sqrt{x}\) + C.
b. ∫ [-∞, 0] x\(e^{-x\) dx = -x\(e^{-x\) - \(e^{-x\) + C.
learn more about integral here
brainly.com/question/33152241
#SPJ4
The above question is incomplete, the complete question is:
Evaluate the following integral:
\((a) \( \int e^{\sqrt{x}} d x \) (b) \( \int_{-\infty}^{0} x e^{-x} d x \)\)
Fill in the missing number. % of 98 = 49
Answers
50%
since 98/2 = 49
Thats it
Please help meh lol.

Answers
Answer:111m^2
Step-by-step explanation:
About how many times greater was change in price per gallon in 2007 than 2000? Show your work or explain how u determind your answer.
Answers
The required, in 2007 the price per gallon was 7b more than the price of a gallon of fuel in the year 2000. Where b is the inflation factor.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
Here,
Let 'a' be the cost per gallon of fuel in the year 2000, and 'b' be the inflation rate per year. If the rate of inflation is constant then
After 7 year inflation = 7b
Cost of fuel in 2007 = a + 7b
Now,
according to the question
Change in cost of fuel
= cost in 2007 - cost in 2000
= a + 7b - a
= 7b
Thus, the required, in 2007 the price per gallon was 7b more than the price of a gallon of fuel in the year 2000. Where b is the inflation factor.
Learn more about simplification here:
https://brainly.com/question/12501526
#SPJ1
2) A big league pitching coach tries to limit his pitchers to 110
pitches per game. If the pitcher has already thrown 52
pitches, write and solve an inequality to find how many more
pitches he can throw before reaching the limit.
Answers
Write an exponential expression: choose a number between 0 and 10 to be the base and another number between 0 and 10, different from the base, to be the exponent. Label the base and the exponent. Then write the exponential expression in expanded form and standard form.
Answers
Answer:
In expanded form:
2^3 = 2 * 2 * 2 = 8
In standard form :
2^3
Step-by-step explanation:
Given the numbers in range (0 to 10)
Write an exponential expression :
Choosing from the range for the Base and the exponent
Base = 2
Exponent = 3
where ; 2 = base. ; 3 = exponent
In expanded form:
2^3 = 2 * 2 * 2 = 8
In standard form :
2^3
Find the radius of a sphere with a volume of 4.51 cubic centimeters.
Answers
Answer:
Radius = 1.02493
Marsha has two cubes with one number on each side,each cube is numbered from 1 to 6 marsha rolls both number cubes at the same time. What is the probability that the total of numbers facing up will equal 12
Answers
Answer:
1/36
Step-by-step explanation:
If the cubes are numbered from 1 to 6 there is just one way that the sum of both of them equals 12 and this is when Marsha gets 6 in the first cube and 6 in the other.
Thus, to know what the probability that the total of numbers facing up will equal 12 we would have to calculate the probability that the first cube is 6 AND the second one is also 6.
The probability that the first cube has the number 6 is: 1/6
The probability that the second cube has the number 6 is: 1/6
We need to multiply this numbers because they both have to be 6 (rule of multiplication),
so: \(\frac{1}{6}(\frac{1}{6} )= \frac{1}{36}\)
Thus, the probability that the sum of them equals 12 is 1/36
Please help me with this homework

Answers
Answer: Circumference = 18 π cm
Step-by-step explanation:
We can use this formula to find the circumference of a circle:
➜ r is equal to the radius, also known as half the width of a circle.
C = 2πr
We will substitute our known values and solve for C by multiplying. Since the answer option includes π in our units, we do not multiply this into the 18.
C = 2πr
C = 2π(9)
C = 18 π cm
Answer: 18π
Step-by-step explanation:
The circumference of a circle is equal to 2πr, with r being equal to the radius. The radius of a circle is defined as the length from any point on the circle to its middlemost point. In this case, we are given the value of the radius as defined by the line. The radius equals 9, which we can plug into the equation.
C= 2πr
C = 2π(9)
C = 18π = 56.55
Hope this helps!
Find the volume of the solid of revolution generated by revolving about the x-axis the region under the following curve. y= x from x=0 to x=20 (The solid generated is called a paraboloid.) The volume is (Type an exact answer in terms of n.)
Answers
To start, let's sketch the graph of the curve y = x from x = 0 to x = 20. This is simply a diagonal line that passes through the points (0,0) and (20,20), as shown below:
```
|
20 | *
| *
| *
| *
|*
0 --------------
0 10 20
```
Now, we want to revolve this curve around the x-axis to create a solid shape. Specifically, we want to create a paraboloid, which is a three-dimensional shape that looks like an upside-down bowl.
To find the volume of this paraboloid, we need to use calculus. The basic idea is to slice the solid into very thin disks, and then add up the volumes of all the disks to get the total volume.
To do this, we'll use the formula for the volume of a cylinder, which is:
V = πr^2h
where r is the radius of the cylinder and h is its height. In our case, each disk is a cylinder with radius r and height h, where:
- r is equal to the y-value of the curve (i.e. r = y = x), since the disk extends from the x-axis to the curve.
- h is the thickness of the disk, which is a very small change in x. We can call this dx.
So, the volume of each disk is:
dV = πr^2dx
= πx^2dx
To find the total volume of the paraboloid, we need to add up the volumes of all the disks. This is done using an integral:
V = ∫(from x=0 to x=20) dV
= ∫(from x=0 to x=20) πx^2dx
Evaluating this integral gives us:
V = π/3 * 20^3
= 8000π/3
So the exact volume of the paraboloid is 8000π/3.
To know more about paraboloid visit:-
https://brainly.com/question/30634603
#SPJ11
Simplifies the expressions please!!!!!!!!
4x^3y^2 x 3x^6y^3/24x^11y^2
(3rs^2t^4)^2/21r^2s^3t^11
(10a^4b^6)(3a^5b^2) -7a^9b^8
(-5x^4y^7)^2 + 9x^8y^14
20 POINTS!!!!!
Answers
Answer:
In order:
\(\frac{y^{3}}{2x^{2}}\)
\(\frac{9r^2s}{2t^{3}}\)
\(23a^9b^8\)
\(34x^8y^{14}\)
Step-by-step explanation:
\(\frac{4x^3y^2 * 3x^6y^3}{24x^{11}y^2} \\\\\frac{12x^9y^5}{24x^{11}y^2} \\\\\frac{x^9y^5}{2x^{11}y^2} \\\\\\frac{y^5}{2x^{11-9}y^2} \\\\\frac{y^5}{2x^{2}y^2} \\\\\frac{y^{5-2}}{2x^{2}y^2} \\\\\frac{y^{3}}{2x^{2}}\)
\((3rs^2t^4)^2/21r^2s^3t^11\\\\\frac{9r^2s^4t^8}{2s^3t^{11}} \\\\\frac{9r^2s^{4-3}t^8}{2s^3t^{11-8}} \\\\\frac{9r^2s}{2t^{3}}\)
\((10a^4b^6)(3a^5b^2) -7a^9b^8\\\\30a^9b^8-7a^9b^8\\\\23a^9b^8\)
\((-5x^4y^7)^2 + 9x^8y^{14}\\\\25x^8y^{14}+9x^8y^{14}\\\\34x^8y^{14}\)
Hope this helps!
If purchased a TV on my debit card, money will be taken out of my account immediately
True
False
Answers
Answer: Debit card transactions usually go through a period where the purchase is pending before the funds are removed from your account. The funds will not be taken out of your account immediately. Therefore it is false
the table shows the number of bottles of different kinds of juices sold at a cafeteria on Monday. If the cafeteria has 80 customers on Tuesday, the prediction for Tuesday is not supported by the data in the table?
Answers
What are the 3 root types?
Answers
Answer:
Irrational, Rational, and Complex Roots
Step-by-step explanation:
Irrational roots cannot be written as a fraction, for example, √2 is an irrational root because 2 is not a square number
Rational roots can be written as a fraction. For example, √4 is a rational root because it can be either -2 or 2 which are both rational.
Complex/imaginary roots take the form of \(a+bi\) where "a" is the real part and "b" is the imaginary part. For example, √(-1) = i which is complex/imaginary.
hi pls help me out with this

Answers
Fitness mania charges 20$ to join their gym and then 15$ per month.
1. Write an equation in slope intercept form.
2. How much will it cost to belong to Fitness Mania for one year?
3. If a different gym LVAC, charges 0$ to join and 20$ a month, which gym would be the cheaper choice for one year?
Answers
Fitness mania is cheaper as $200 < $240